2020_2021学年人教版七年级数学下册教学课件9.2第2课时 一元一次不等式的应用(共16张ppt)
文档属性
| 名称 | 2020_2021学年人教版七年级数学下册教学课件9.2第2课时 一元一次不等式的应用(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 433.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第九章 不等式与不等式组
9.2 一元一次不等式
第2课时 一元一次不等式的应用
一、教学目标
重点
难点
二、教学重难点
1.能根据实际问题中的数量关系列出一元一次不等式,解决简单问题.
2.经历“选用不等式解决实际问题”的过程,初步体会一元一次不等式的应用价值.
会列不等式解决实际问题.
在实际问题中寻找不等关系,列出不等式.
活动1
新课导入
三、教学设计
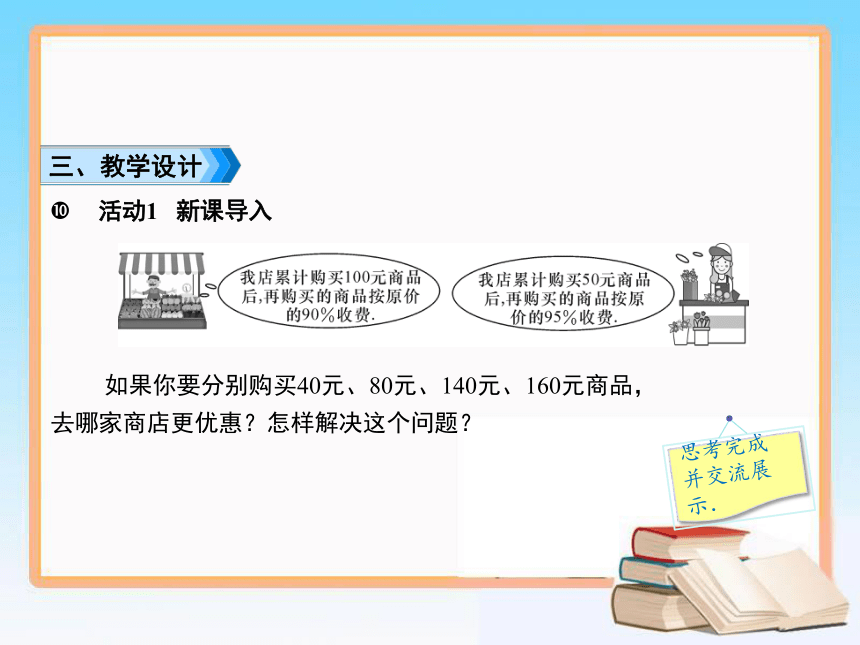
如果你要分别购买40元、80元、140元、160元商品,
去哪家商店更优惠?怎样解决这个问题?
思考完成并交流展示.
活动2
探究新知
1.某次知识竞赛共有20道题,每道题答对加10分,答错或不答均扣5分,小明想要得分超过90分,他至少要答对多少道题?
提出问题:
(1)“超过90分”用不等式表示是什么?该题中的不等关系是什么?
(2)如果设答对了x道题,那么如何用含x的式子表示得分?
(3)请列出表示题意的不等式,并解出该不等式;
(4)你能归纳出列不等式解应用题的步骤吗?
思考完成并交流展示.
2.教材P125 例3.
提出问题:
(1)例题中的不等关系是什么?
(2)式子V+3×5×3≤3×5×10中的“≤”能换成“<”吗?为什么?
(3)V的取值范围应满足哪两个条件?为什么?
(4)用数轴表示V的取值范围V≥0且V≤105时,在表示0和105的点上画实心圆点,表示什么含义?
思考完成并交流展示.
例
甲、乙两超市以同样价格出售同样的商品,并且给出了不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按90%收费;在乙超市累计购物超过50元后,超出50元的部分按95%收费,顾客到哪家超市购物花费少?
分析:甲乙两超市的优惠价格不一样,因此需要分类讨论:
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元,
(3)当购物超过100元.
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠,物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元
①若
50+0.95(x-50)>100+0.9(x-100)
即x>150
在甲超市购物花费少;
②若
50+0.95(x-50)<100+0.9(x-100)
即x<150
在乙超市购物花费少;
③若
50+0.95(x-50)=100+0.9(x-100)
即x=150
在甲、乙两超市购物花费一样.
活动3
知识归纳
列不等式解应用题的一般步骤:
(1)审题:弄清题意及题目中的_________;
(2)设未知数:可______设,也可______设;
(3)列出_______;
(4)解不等式,并验证解(集)的________;
(5)写出______.
不等关系
直接
间接
不等式
合理性
答案
例1 教材P124 例2.
活动4
例题与练习
例2 有10名菜农,每人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,要使总收入不低于15.6万元,则最多只能安排多少人种甲种蔬菜?
解:设安排x人种甲种蔬菜,则种乙种蔬菜的为(10-x)人.
根据题意,得0.5×3x+0.8×2(10-x)≥15.6,解得x≤4.
答:最多只能安排4人种甲种蔬莱.
例3 某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A
B
进价(万元/套)
1.5
1.2
售价(万元/套)
1.65
1.4
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
解:(1)设该商场计划购进A,B两种品牌的教学设备分别为x套、y套.
由题意,得
解得
答:该商场计划购进A,B两种品牌的教学设备分别为20套、30套;
(2)设A种设备购进数量减少a套,则B种设备购进数量增加1.5a套.
由题意,得1.5×(20-a)+1.2×(30+1.5a)≤69,解得a≤10.
答:A种设备购进数量至多减少10套.
练
习
1.教材P125 练习第1,2题.
2.篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队预计在本赛季32场比赛中至少得到48分,才有希望进入季后赛.假设这个队在将要举行的比赛中胜x场,要达到目标,x应满足的关系式是(
)
A.2x+(32-x)≥48
B.2x-(32-x)≥48
C.2x+(32-x)≤48
D.2x≥48
A
练
习
3.光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其他天气平均每天可发电5度,已知某月(按30天计)共发电550度.
(1)求这个月晴天的天数;
(2)已知该家庭每月平均用电量为150度,若按每月发电550度计,至少需要几年才能收回成本(不计其他费用,结果取整数).
练
习
解:(1)设这个月的晴天有x天.
根据题意,得30x+5(30-x)=550,
解得x=16.
答:这个月晴天有16天;
(2)设y年可收回成本,根据题意,
得(550-150)×(0.52+0.45)×12y≥40
000,
解得y≥8.6.
答:至少需要9年可收回成本.
活动5
课堂小结
应用一元一次不等式解决实际问题的步骤:
四、作业布置与教学反思
1.作业布置
(1)教材P126 习题9.2第5,6,7,8题;
2.教学反思
第九章 不等式与不等式组
9.2 一元一次不等式
第2课时 一元一次不等式的应用
一、教学目标
重点
难点
二、教学重难点
1.能根据实际问题中的数量关系列出一元一次不等式,解决简单问题.
2.经历“选用不等式解决实际问题”的过程,初步体会一元一次不等式的应用价值.
会列不等式解决实际问题.
在实际问题中寻找不等关系,列出不等式.
活动1
新课导入
三、教学设计
如果你要分别购买40元、80元、140元、160元商品,
去哪家商店更优惠?怎样解决这个问题?
思考完成并交流展示.
活动2
探究新知
1.某次知识竞赛共有20道题,每道题答对加10分,答错或不答均扣5分,小明想要得分超过90分,他至少要答对多少道题?
提出问题:
(1)“超过90分”用不等式表示是什么?该题中的不等关系是什么?
(2)如果设答对了x道题,那么如何用含x的式子表示得分?
(3)请列出表示题意的不等式,并解出该不等式;
(4)你能归纳出列不等式解应用题的步骤吗?
思考完成并交流展示.
2.教材P125 例3.
提出问题:
(1)例题中的不等关系是什么?
(2)式子V+3×5×3≤3×5×10中的“≤”能换成“<”吗?为什么?
(3)V的取值范围应满足哪两个条件?为什么?
(4)用数轴表示V的取值范围V≥0且V≤105时,在表示0和105的点上画实心圆点,表示什么含义?
思考完成并交流展示.
例
甲、乙两超市以同样价格出售同样的商品,并且给出了不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按90%收费;在乙超市累计购物超过50元后,超出50元的部分按95%收费,顾客到哪家超市购物花费少?
分析:甲乙两超市的优惠价格不一样,因此需要分类讨论:
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元,
(3)当购物超过100元.
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠,物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元
①若
50+0.95(x-50)>100+0.9(x-100)
即x>150
在甲超市购物花费少;
②若
50+0.95(x-50)<100+0.9(x-100)
即x<150
在乙超市购物花费少;
③若
50+0.95(x-50)=100+0.9(x-100)
即x=150
在甲、乙两超市购物花费一样.
活动3
知识归纳
列不等式解应用题的一般步骤:
(1)审题:弄清题意及题目中的_________;
(2)设未知数:可______设,也可______设;
(3)列出_______;
(4)解不等式,并验证解(集)的________;
(5)写出______.
不等关系
直接
间接
不等式
合理性
答案
例1 教材P124 例2.
活动4
例题与练习
例2 有10名菜农,每人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,要使总收入不低于15.6万元,则最多只能安排多少人种甲种蔬菜?
解:设安排x人种甲种蔬菜,则种乙种蔬菜的为(10-x)人.
根据题意,得0.5×3x+0.8×2(10-x)≥15.6,解得x≤4.
答:最多只能安排4人种甲种蔬莱.
例3 某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A
B
进价(万元/套)
1.5
1.2
售价(万元/套)
1.65
1.4
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
解:(1)设该商场计划购进A,B两种品牌的教学设备分别为x套、y套.
由题意,得
解得
答:该商场计划购进A,B两种品牌的教学设备分别为20套、30套;
(2)设A种设备购进数量减少a套,则B种设备购进数量增加1.5a套.
由题意,得1.5×(20-a)+1.2×(30+1.5a)≤69,解得a≤10.
答:A种设备购进数量至多减少10套.
练
习
1.教材P125 练习第1,2题.
2.篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队预计在本赛季32场比赛中至少得到48分,才有希望进入季后赛.假设这个队在将要举行的比赛中胜x场,要达到目标,x应满足的关系式是(
)
A.2x+(32-x)≥48
B.2x-(32-x)≥48
C.2x+(32-x)≤48
D.2x≥48
A
练
习
3.光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其他天气平均每天可发电5度,已知某月(按30天计)共发电550度.
(1)求这个月晴天的天数;
(2)已知该家庭每月平均用电量为150度,若按每月发电550度计,至少需要几年才能收回成本(不计其他费用,结果取整数).
练
习
解:(1)设这个月的晴天有x天.
根据题意,得30x+5(30-x)=550,
解得x=16.
答:这个月晴天有16天;
(2)设y年可收回成本,根据题意,
得(550-150)×(0.52+0.45)×12y≥40
000,
解得y≥8.6.
答:至少需要9年可收回成本.
活动5
课堂小结
应用一元一次不等式解决实际问题的步骤:
四、作业布置与教学反思
1.作业布置
(1)教材P126 习题9.2第5,6,7,8题;
2.教学反思
