2020-2021学年 八年级数学人教版下册 16.1 二次根式 二次根式的定义 同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年 八年级数学人教版下册 16.1 二次根式 二次根式的定义 同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 161.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 20:39:01 | ||
图片预览


文档简介
16.1
二次根式
二次根式的定义
基础训练
知识点1
二次根式的定义
1.下列式子一定是二次根式的是( )
A.
B.
C.
D.
2.下列式子不一定是二次根式的是( )
A.
B.
C.
D.
3.下列式子:,,,,,,中,一定是二次根式的有( )
A.2个
B.3个
C.4个
D.5个
知识点2
二次根式有意义的条件
4.(2016·重庆)若二次根式有意义,则a的取值范围是( )
A.a≥2
B.a≤2
C.a>2
D.a≠2
5.(中考·巴中)要使式子有意义,则m的取值范围是( )
A.m>-1
B.m≥-1
C.m>-1且m≠1
D.m≥-1且m≠1
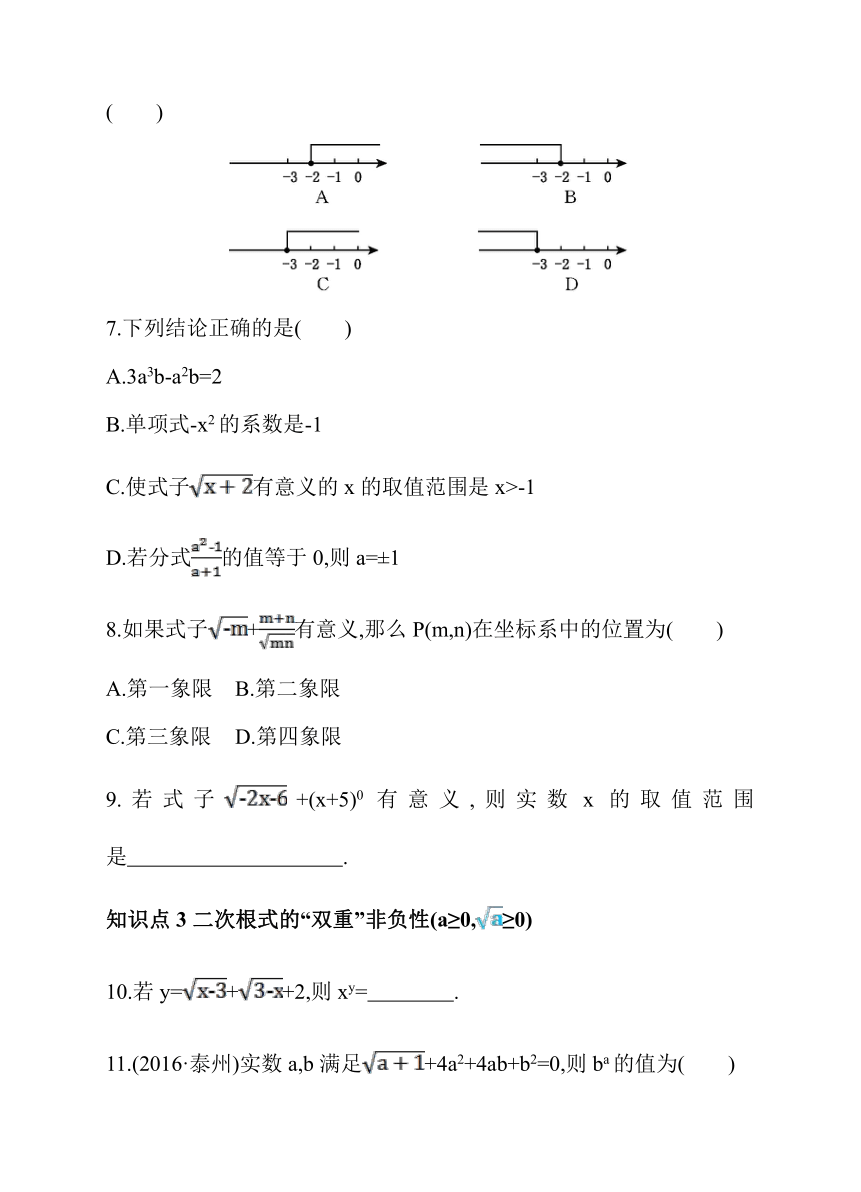
6.如果式子有意义,那么x的取值范围在数轴上表示正确的是( )
7.下列结论正确的是( )
A.3a3b-a2b=2
B.单项式-x2的系数是-1
C.使式子有意义的x的取值范围是x>-1
D.若分式的值等于0,则a=±1
8.如果式子+有意义,那么P(m,n)在坐标系中的位置为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
9.若式子+(x+5)0有意义,则实数x的取值范围是 .
知识点3二次根式的“双重”非负性(a≥0,≥0)
10.若y=++2,则xy= .?
11.(2016·泰州)实数a,b满足+4a2+4ab+b2=0,则ba的值为( )
A.2
B.
C.-2
D.-
12.已知实数x,y满足|x-4|+=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16
B.20
C.16
D.以上答案均不对
易错点
考虑不全造成答案不完整
13.若式子有意义,则实数x的取值范围是( )
A.x≥-1
B.x≥-1且x≠3
C.x>-1
D.x>-1且x≠3
提升训练
14.已知y=2+3+,求+的值.
15.已知+=0,求x,y的值.
16.已知a为实数,求式子-+的值.
17.当x取什么实数时,式子+2的取值最小?并求出这个最小值.
探究培优
18.已知a、b为一等腰三角形的两边长,且满足等式
2+3=b-4,求此等腰三角形的周长.
19.已知m满足
且=-,求m的值.
参考答案
1.【答案】C
解:判断是否为二次根式必须满足两个条件:一是被开方数为非负数,二是根指数为2,只有C符合条件.
2.【答案】A
解:根据二次根式的定义进行识别.中a<0时不是二次根式.
3.【答案】C
4.【答案】A
解:∵二次根式∴a﹣2≥0,即a≥2,
则a的范围是a≥2,
故选A
5.【答案】D
解:根据题意得:解得m≥-1且m≠1.故选D.
6.【答案】C
解:先根据二次根式的意义,其有意义的条件是被开方数大于等于0,因此可得2x+6≥0,可解不等式得x≥-3,因此可在数轴上表示为C.
故选C
7.【答案】B
8.【答案】C
解:根据二次根式及分式有意义的条件得-m≥0且mn>0,解得m<0且n<0,所以P(m,n)在第三象限,故选项C正确.
9.【答案】x≤-3且x≠-5
解:由题意得解得x≤-3且x≠-5.
10.【答案】9
解:由题意得解得x=3,∴y=2.∴xy=32=9.
11.【答案】B
解:整理得+(2a+b)2=0,
所以a+1=0,2a+b=0,
解得a=-1,b=2.
所以ba=2-1=.
故选B.
12.【答案】B
解:根据非负数的意义列出关于x,y的方程,并求出x,y的值,再根据x是腰长和底边长两种情况讨论求解.即x-4=0,y-8=0,解得x=4,y=8.①若4是腰长,则三角形的三边长分别为4,4,8,不能组成三角形;②若4是底边长,则三角形的三边长分别为4,8,8,能组成三角形,且周长为4+8+8=20.故选B.
13.【答案】B
解:本题易错在漏掉分母不为0这个条件,由题意知x+1≥0且(x-3)2≠0,解得x≥-1且x≠3.
14.解:由被开方数的非负性,得2x-1≥0,且1-2x≥0,所以x≥,且x≤.所以x=.
将x=代入已知条件,得y=.
所以+=2+3=5.
15.解:因为≥0,≥0,且其和为0,
所以x+1=0,x+y-2=0,解得x=-1,y=3.
所以x,y的值分别为-1,3.
方法总结:a2,|a|,都为非负数,即a2≥0,|a|≥0,≥0(a≥0).可利用“若几个非负数之和为零,则这几个非负数同时为零”解决问题.
16.解:由题意得:-a2≥0,∴a2≤0,又a2≥0,∴a=0,
∴原式=-+0=0.
17.解:由二次根式有意义的条件得3x-1≥0,即x≥,所以当x=时,式子+2的取值最小,最小值为2.
18.解:由题意知
解得a=2,∴b=4,当三边长为2,2,4时不能构成三角形,当三边长为4,4,2时能构成三角形,∴此等腰三角形的周长为10.
19.解:依题意得:
∴x+y=2018,把含有m的两方程相加得:5(x+y)+1+m=0,
∴m=-10091.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
二次根式
二次根式的定义
基础训练
知识点1
二次根式的定义
1.下列式子一定是二次根式的是( )
A.
B.
C.
D.
2.下列式子不一定是二次根式的是( )
A.
B.
C.
D.
3.下列式子:,,,,,,中,一定是二次根式的有( )
A.2个
B.3个
C.4个
D.5个
知识点2
二次根式有意义的条件
4.(2016·重庆)若二次根式有意义,则a的取值范围是( )
A.a≥2
B.a≤2
C.a>2
D.a≠2
5.(中考·巴中)要使式子有意义,则m的取值范围是( )
A.m>-1
B.m≥-1
C.m>-1且m≠1
D.m≥-1且m≠1
6.如果式子有意义,那么x的取值范围在数轴上表示正确的是( )
7.下列结论正确的是( )
A.3a3b-a2b=2
B.单项式-x2的系数是-1
C.使式子有意义的x的取值范围是x>-1
D.若分式的值等于0,则a=±1
8.如果式子+有意义,那么P(m,n)在坐标系中的位置为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
9.若式子+(x+5)0有意义,则实数x的取值范围是 .
知识点3二次根式的“双重”非负性(a≥0,≥0)
10.若y=++2,则xy= .?
11.(2016·泰州)实数a,b满足+4a2+4ab+b2=0,则ba的值为( )
A.2
B.
C.-2
D.-
12.已知实数x,y满足|x-4|+=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16
B.20
C.16
D.以上答案均不对
易错点
考虑不全造成答案不完整
13.若式子有意义,则实数x的取值范围是( )
A.x≥-1
B.x≥-1且x≠3
C.x>-1
D.x>-1且x≠3
提升训练
14.已知y=2+3+,求+的值.
15.已知+=0,求x,y的值.
16.已知a为实数,求式子-+的值.
17.当x取什么实数时,式子+2的取值最小?并求出这个最小值.
探究培优
18.已知a、b为一等腰三角形的两边长,且满足等式
2+3=b-4,求此等腰三角形的周长.
19.已知m满足
且=-,求m的值.
参考答案
1.【答案】C
解:判断是否为二次根式必须满足两个条件:一是被开方数为非负数,二是根指数为2,只有C符合条件.
2.【答案】A
解:根据二次根式的定义进行识别.中a<0时不是二次根式.
3.【答案】C
4.【答案】A
解:∵二次根式∴a﹣2≥0,即a≥2,
则a的范围是a≥2,
故选A
5.【答案】D
解:根据题意得:解得m≥-1且m≠1.故选D.
6.【答案】C
解:先根据二次根式的意义,其有意义的条件是被开方数大于等于0,因此可得2x+6≥0,可解不等式得x≥-3,因此可在数轴上表示为C.
故选C
7.【答案】B
8.【答案】C
解:根据二次根式及分式有意义的条件得-m≥0且mn>0,解得m<0且n<0,所以P(m,n)在第三象限,故选项C正确.
9.【答案】x≤-3且x≠-5
解:由题意得解得x≤-3且x≠-5.
10.【答案】9
解:由题意得解得x=3,∴y=2.∴xy=32=9.
11.【答案】B
解:整理得+(2a+b)2=0,
所以a+1=0,2a+b=0,
解得a=-1,b=2.
所以ba=2-1=.
故选B.
12.【答案】B
解:根据非负数的意义列出关于x,y的方程,并求出x,y的值,再根据x是腰长和底边长两种情况讨论求解.即x-4=0,y-8=0,解得x=4,y=8.①若4是腰长,则三角形的三边长分别为4,4,8,不能组成三角形;②若4是底边长,则三角形的三边长分别为4,8,8,能组成三角形,且周长为4+8+8=20.故选B.
13.【答案】B
解:本题易错在漏掉分母不为0这个条件,由题意知x+1≥0且(x-3)2≠0,解得x≥-1且x≠3.
14.解:由被开方数的非负性,得2x-1≥0,且1-2x≥0,所以x≥,且x≤.所以x=.
将x=代入已知条件,得y=.
所以+=2+3=5.
15.解:因为≥0,≥0,且其和为0,
所以x+1=0,x+y-2=0,解得x=-1,y=3.
所以x,y的值分别为-1,3.
方法总结:a2,|a|,都为非负数,即a2≥0,|a|≥0,≥0(a≥0).可利用“若几个非负数之和为零,则这几个非负数同时为零”解决问题.
16.解:由题意得:-a2≥0,∴a2≤0,又a2≥0,∴a=0,
∴原式=-+0=0.
17.解:由二次根式有意义的条件得3x-1≥0,即x≥,所以当x=时,式子+2的取值最小,最小值为2.
18.解:由题意知
解得a=2,∴b=4,当三边长为2,2,4时不能构成三角形,当三边长为4,4,2时能构成三角形,∴此等腰三角形的周长为10.
19.解:依题意得:
∴x+y=2018,把含有m的两方程相加得:5(x+y)+1+m=0,
∴m=-10091.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
