2020-2021学年 沪科版八年级数学下册18.1 第2课时 勾股定理应用课件(共14张ppt)
文档属性
| 名称 | 2020-2021学年 沪科版八年级数学下册18.1 第2课时 勾股定理应用课件(共14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 795.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第18章
勾股定理
18.1
第2课时
勾股定理的应用
情景导入
数学来源于生活,勾股定理的应用在生活中无处不在,观看下面视频,你们能理解曾小贤和胡一菲的做法吗?
例题讲解
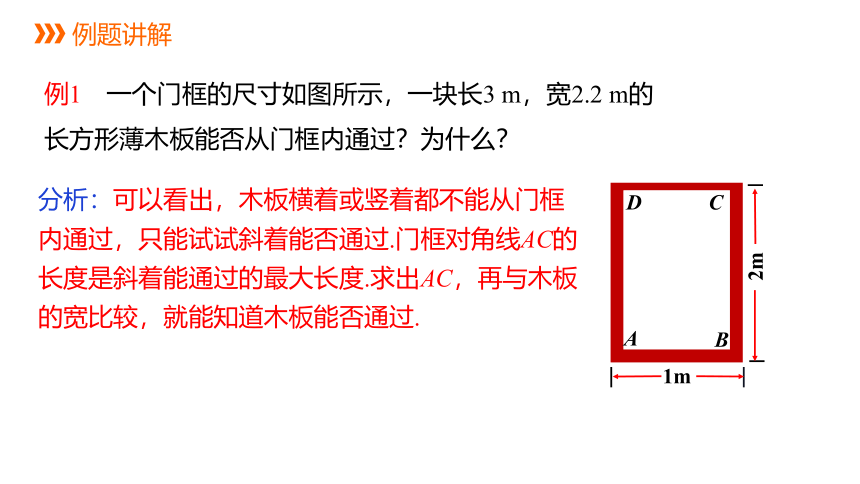
例1
一个门框的尺寸如图所示,一块长3
m,宽2.2
m的长方形薄木板能否从门框内通过?为什么?
分析:可以看出,木板横着或竖着都不能从门框内通过,只能试试斜着能否通过.门框对角线AC的长度是斜着能通过的最大长度.求出AC,再与木板的宽比较,就能知道木板能否通过.
2m
1m
A
B
D
C
2m
1m
A
B
D
C
解:在Rt△ABC中,根据勾股定理,
AC2
=AB2+BC2
=12+22=5.
AC=
≈2.
24.
因为AC大于木板的宽2.
2
m,所以木板能从门框内通过.
例2
现有一楼房发生火灾,消防队员决定用消防车上
的云梯救人,如图
(1).
已知云梯最多只能伸长到
10
m,消防车高3m.
救人时云梯伸至最长,在完成从9
m高处救人后,还要从12
m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1m)
分析:如图(2),设A是云梯的下端点,AB是伸长后的云梯,B是第一次救人的地点,D是第二次救人的地点,过点A的水平线与楼房ED的交点为O
.则OB=9-3
=
6(m)
,
OD
=12-3
=
9(m).
根据勾股定理,得
AO2
=
AB2
-
OB2
=
102
-62
=
64.
解方程,得
AO
=
8(m).
设AC
=x,则OC
=
8-x,于是根据勾股定理,得
OC2
+
OD2
=
CD2,
即(8
-x)2
+92
=
102,
从而可以解出x.
例3
已知:如图,
在Rt
△ABC中,两直角边AC
=
5,
BC
=
12.
求斜边上的高CD的长
┐
A
B
C
D
┐
解:在Rt△ABC中,
AB2
=AC2
+BC2
=
52
+
122
=
169,
AB
=
=
13.
又∵
Rt△ABC的面积
求直角三角形斜边上的高常用等积法.
随堂演练
1.
如果梯子的底端离一幢楼5米,那么13米长的梯子可以达到该楼的高度是( )
A.12米
B.13米
C.14米
D.15米
A
2.
由于受台风的影响,一棵树在离地面6
m处折断(如图),树顶落在离树干底部8
m处,则这棵树在折断前的高度是( )
A.8
m
B.10
m
C.16
m
D.18
m
C
3.
小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面后还多1
m,当他把绳子的下端拉开4
m后,发现下端刚好接触地面,则旗杆的高为( )
A.7
m
B.7.5
m
C.8
m
D.9
m
B
4.已知点(2,5),(-4,-3),则这两点的距离为_______.
10
5.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何.”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.若设AC=x,则可列方程为_______________.
x2+32=(10-x)2
6.
如图,有两棵树,一棵高8米,另一棵2米,两棵对相距8米.
一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
7.
如图,折叠长方形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8
cm,BC=10
cm,求CE的长.
解:由题意,知BC=AD=AF=10
cm,DE=EF.
在Rt△ABF中,BF=
(cm),
∴CF=BC-BF=4
cm.
设CE=x
cm,则DE=EF=(8-x)cm.
在Rt△FEC中,
由勾股定理,
得CF2+CE2=EF2,即42+x2=(8-x)2,
解得x=3,即CE=3
cm.
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
课堂小结
第18章
勾股定理
18.1
第2课时
勾股定理的应用
情景导入
数学来源于生活,勾股定理的应用在生活中无处不在,观看下面视频,你们能理解曾小贤和胡一菲的做法吗?
例题讲解
例1
一个门框的尺寸如图所示,一块长3
m,宽2.2
m的长方形薄木板能否从门框内通过?为什么?
分析:可以看出,木板横着或竖着都不能从门框内通过,只能试试斜着能否通过.门框对角线AC的长度是斜着能通过的最大长度.求出AC,再与木板的宽比较,就能知道木板能否通过.
2m
1m
A
B
D
C
2m
1m
A
B
D
C
解:在Rt△ABC中,根据勾股定理,
AC2
=AB2+BC2
=12+22=5.
AC=
≈2.
24.
因为AC大于木板的宽2.
2
m,所以木板能从门框内通过.
例2
现有一楼房发生火灾,消防队员决定用消防车上
的云梯救人,如图
(1).
已知云梯最多只能伸长到
10
m,消防车高3m.
救人时云梯伸至最长,在完成从9
m高处救人后,还要从12
m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1m)
分析:如图(2),设A是云梯的下端点,AB是伸长后的云梯,B是第一次救人的地点,D是第二次救人的地点,过点A的水平线与楼房ED的交点为O
.则OB=9-3
=
6(m)
,
OD
=12-3
=
9(m).
根据勾股定理,得
AO2
=
AB2
-
OB2
=
102
-62
=
64.
解方程,得
AO
=
8(m).
设AC
=x,则OC
=
8-x,于是根据勾股定理,得
OC2
+
OD2
=
CD2,
即(8
-x)2
+92
=
102,
从而可以解出x.
例3
已知:如图,
在Rt
△ABC中,两直角边AC
=
5,
BC
=
12.
求斜边上的高CD的长
┐
A
B
C
D
┐
解:在Rt△ABC中,
AB2
=AC2
+BC2
=
52
+
122
=
169,
AB
=
=
13.
又∵
Rt△ABC的面积
求直角三角形斜边上的高常用等积法.
随堂演练
1.
如果梯子的底端离一幢楼5米,那么13米长的梯子可以达到该楼的高度是( )
A.12米
B.13米
C.14米
D.15米
A
2.
由于受台风的影响,一棵树在离地面6
m处折断(如图),树顶落在离树干底部8
m处,则这棵树在折断前的高度是( )
A.8
m
B.10
m
C.16
m
D.18
m
C
3.
小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面后还多1
m,当他把绳子的下端拉开4
m后,发现下端刚好接触地面,则旗杆的高为( )
A.7
m
B.7.5
m
C.8
m
D.9
m
B
4.已知点(2,5),(-4,-3),则这两点的距离为_______.
10
5.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何.”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.若设AC=x,则可列方程为_______________.
x2+32=(10-x)2
6.
如图,有两棵树,一棵高8米,另一棵2米,两棵对相距8米.
一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
7.
如图,折叠长方形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8
cm,BC=10
cm,求CE的长.
解:由题意,知BC=AD=AF=10
cm,DE=EF.
在Rt△ABF中,BF=
(cm),
∴CF=BC-BF=4
cm.
设CE=x
cm,则DE=EF=(8-x)cm.
在Rt△FEC中,
由勾股定理,
得CF2+CE2=EF2,即42+x2=(8-x)2,
解得x=3,即CE=3
cm.
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
课堂小结
