2020-2021学年 苏科版数学七年级下册-9.3 多项式乘多项式-课件(共15张ppt)
文档属性
| 名称 | 2020-2021学年 苏科版数学七年级下册-9.3 多项式乘多项式-课件(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
9.3
多项式乘多项式
1.单项式乘单项式法则
温故知新
2.单项式乘多项式法则
(1)
各系数相乘仍作为积的系数;
(2)
相同字母的幂相乘;
(3)
只在一个单项式里含有的字母要连同它的指数写在积里(注意
不要把这个因式丢掉)
单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.
3、
已知
m
·(a+b)
=am+bm
如果将m换成(c+d),你能计算(a+b)(c+d)吗?
前情测评
m(c+d)=mc+md
=(a+b)c+(a+b)d
=ac+bc+ad+bd
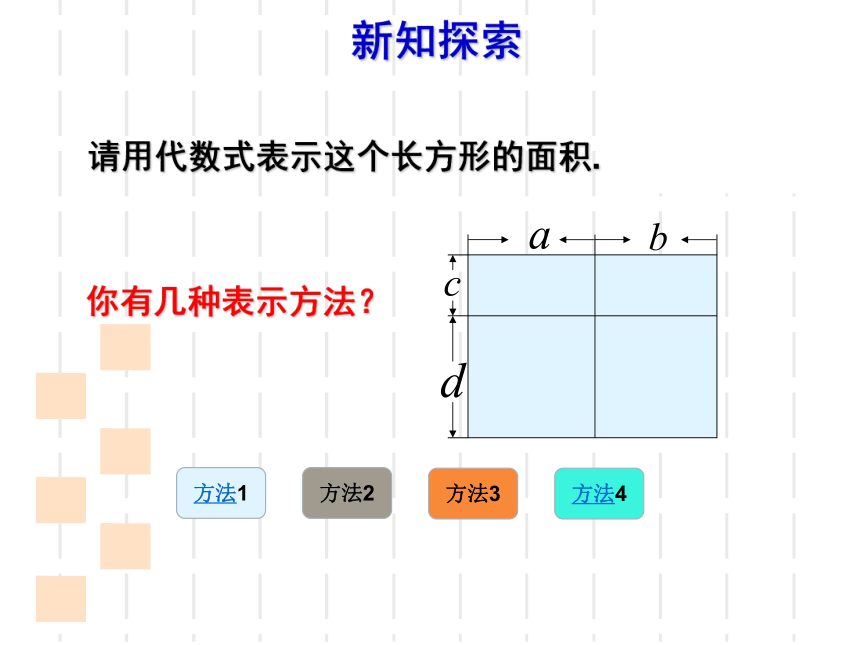
请用代数式表示这个长方形的面积.
你有几种表示方法?
方法1
方法2
方法3
方法4
新知探索
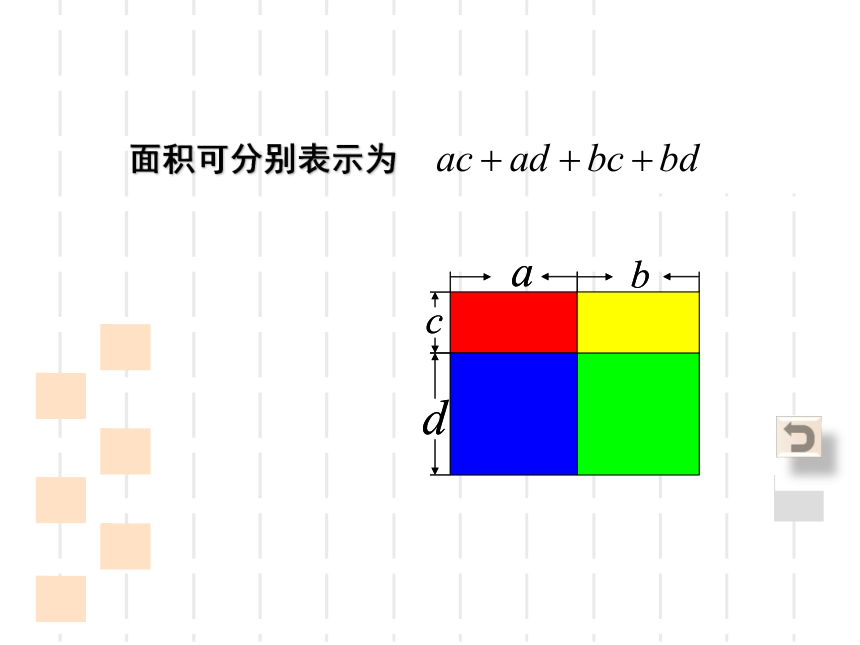
面积可以表示为
面积可分别表示为
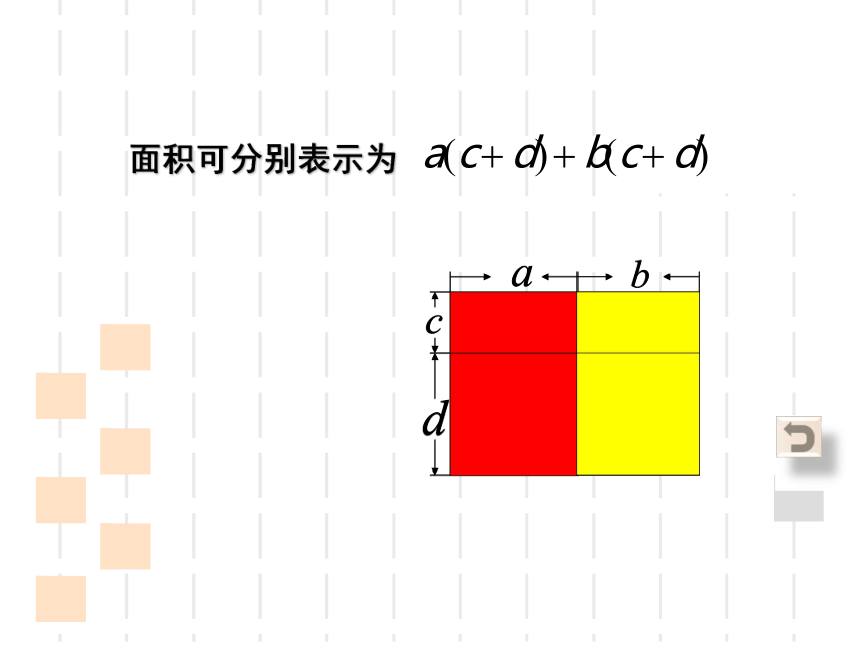
面积可分别表示为
面积可分别表示为
思考:如何进行多项式乘多项式的运算?
=
+
+
+
上面的运算过程也可以表示为:
交流思考
试一试:如何计算下列各式,请说明理由。
(1)(a+4)(a+3)
(2)(3x+1)(x-2)
新知归纳
多项式乘多项式的法则
多项式与多项式相乘,
先用一个多项式的每一项乘另一个多项式的每一项,
再把所得的积相加.
例1:计算
(1)
(2)
友情提醒:1.不漏项
2.符号
3.相乘的结果中,要合并同类项.
解:(1)原式=x?x+x?(-3)+2?x+2?(-3)
=x2-3x+2x-6
=x2-x-6
(2)原式=3x?x+3x?(-2)+(-1)?x+(-1)?(-2)
=3x2-6x-x+2
=3x2-7x+2
例题精讲
例2:计算
(1)
(2)
?
例3 填空:
(1)若
,
则m=___,
n=_______
.
(3)若
,
则(a+1)(b-1)=_____.
3
-28
-4
(2)若
的积中不含
的二次项,求
的值。
?
?
?
检测反馈
1.检验:如何计算下列各式,请说明理由。
(1)(a+4)(a+3)
(2)(3x+1)(x-2)
2.一块长方形地砖的长、宽分别为acm、bcm(a>2,b>2),如果长、宽各裁去2cm,那么剩余部分的面积是多少?
课堂总结
多项式乘多项式
单项式乘多项式
单项式乘单项式
转化
转化
注意:1.不漏项
2.符号
3.相乘的结果中,要合并同类项.
9.3
多项式乘多项式
1.单项式乘单项式法则
温故知新
2.单项式乘多项式法则
(1)
各系数相乘仍作为积的系数;
(2)
相同字母的幂相乘;
(3)
只在一个单项式里含有的字母要连同它的指数写在积里(注意
不要把这个因式丢掉)
单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.
3、
已知
m
·(a+b)
=am+bm
如果将m换成(c+d),你能计算(a+b)(c+d)吗?
前情测评
m(c+d)=mc+md
=(a+b)c+(a+b)d
=ac+bc+ad+bd
请用代数式表示这个长方形的面积.
你有几种表示方法?
方法1
方法2
方法3
方法4
新知探索
面积可以表示为
面积可分别表示为
面积可分别表示为
面积可分别表示为
思考:如何进行多项式乘多项式的运算?
=
+
+
+
上面的运算过程也可以表示为:
交流思考
试一试:如何计算下列各式,请说明理由。
(1)(a+4)(a+3)
(2)(3x+1)(x-2)
新知归纳
多项式乘多项式的法则
多项式与多项式相乘,
先用一个多项式的每一项乘另一个多项式的每一项,
再把所得的积相加.
例1:计算
(1)
(2)
友情提醒:1.不漏项
2.符号
3.相乘的结果中,要合并同类项.
解:(1)原式=x?x+x?(-3)+2?x+2?(-3)
=x2-3x+2x-6
=x2-x-6
(2)原式=3x?x+3x?(-2)+(-1)?x+(-1)?(-2)
=3x2-6x-x+2
=3x2-7x+2
例题精讲
例2:计算
(1)
(2)
?
例3 填空:
(1)若
,
则m=___,
n=_______
.
(3)若
,
则(a+1)(b-1)=_____.
3
-28
-4
(2)若
的积中不含
的二次项,求
的值。
?
?
?
检测反馈
1.检验:如何计算下列各式,请说明理由。
(1)(a+4)(a+3)
(2)(3x+1)(x-2)
2.一块长方形地砖的长、宽分别为acm、bcm(a>2,b>2),如果长、宽各裁去2cm,那么剩余部分的面积是多少?
课堂总结
多项式乘多项式
单项式乘多项式
单项式乘单项式
转化
转化
注意:1.不漏项
2.符号
3.相乘的结果中,要合并同类项.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
