2020-2021学年八年级数学北师大版下册第3章图形的平移与旋转章末综合优生辅导训练(word附答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册第3章图形的平移与旋转章末综合优生辅导训练(word附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 267.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览

文档简介
2021年北师大版八年级数学下册第3章图形的平移与旋转章末综合优生辅导训练(附答案)
1.如图,在△ABC中,∠B=50°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,则∠CB′C′的度数为( )
A.50°
B.60°
C.80°
D.100°
2.如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD,若AD∥BC,则∠ABE的度数为( )
A.25°
B.30°
C.35°
D.40°
3.如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE的周长是10cm,那么四边形ABFD的周长是( )
A.12cm
B.16cm
C.18cm
D.20cm
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
5.图中阴影部分是由4个完全相同的的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在( )
A.区域①处
B.区域②处
C.区域③处
D.区域④处
6.如图,平面内某正方形内有一长为10宽为5的矩形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10
B.11
C.12
D.13
7.如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50°
B.75°
C.65°
D.60°
8.如图,将△ABC绕点A顺时针旋转,得到△ADE,且点D在AC上,下列说法错误的是( )
A.AC平分∠BAE
B.AB=AD
C.BC∥AE
D.BC=DE
9.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列四个结论:
①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC;
其中一定正确的是( )
A.①②
B.②③
C.③④
D.②③④
10.如图,△ABC是等边三角形,点D为AC边上一点,以BD为边作等边△BDE,连接CE.若CD=1,CE=3,则BC=( )
A.2
B.3
C.4
D.5
11.如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为
cm2.
12.正六边形绕其中心旋转一定的角度与原图形重合,则这个旋转角至少为
.
13.若点(﹣m,n+3)与点(2,﹣2m)关于原点对称,则m+n=
.
14.在△ABC中,∠BAC=120°,D为BC的中点,AE=6,把AD绕点A逆时针旋转120°,得到AF,若CF=7,∠ACF=∠AEC,则AC=
.
15.如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.
(1)△ABC旋转了
度.
(2)连接CE,判断△AEC的形状是
.
(3)若∠ACE=20°,则∠AEC的度数为
.
16.如图,在等边△ABC中,AB=12,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为
.
17.如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A'B'C'D',图中阴影部分的面积为
.
18.如图,有一块长为a米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草地的面积为12米2,则a=
.
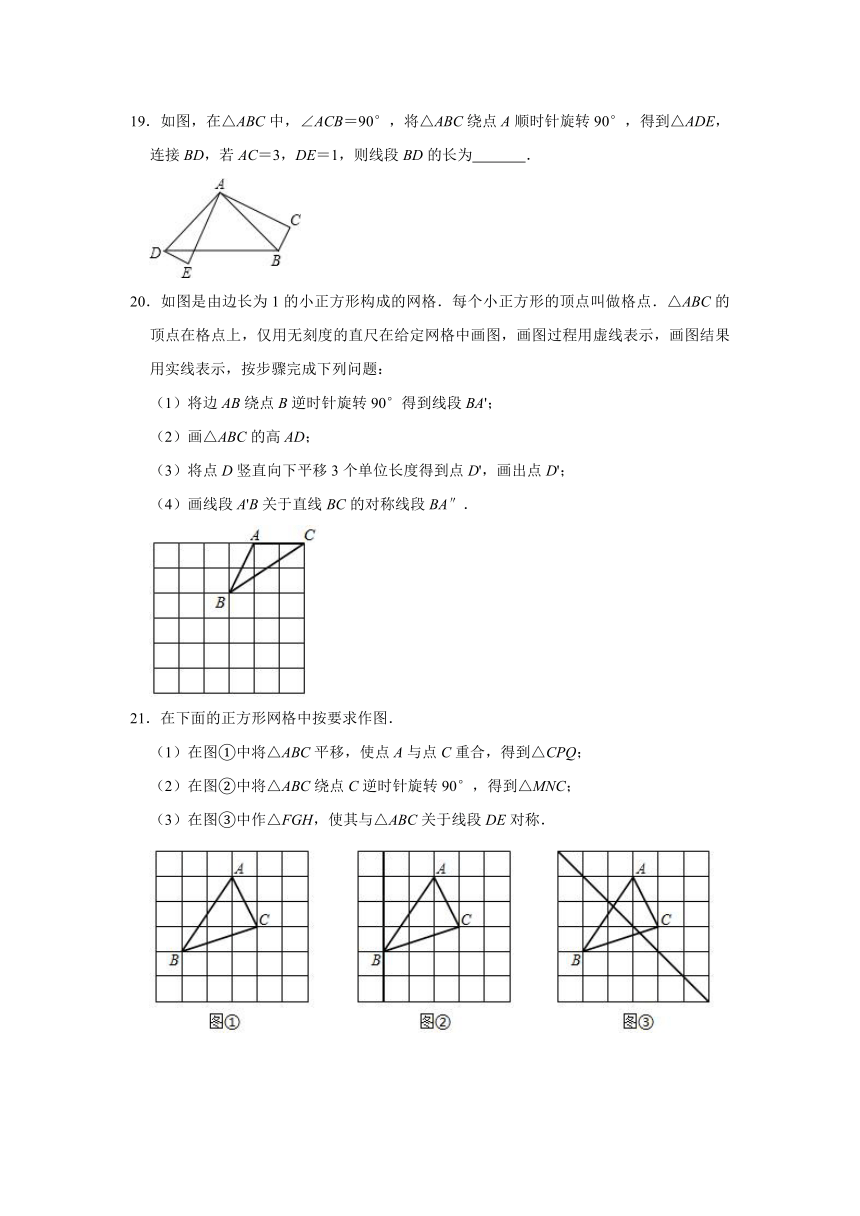
19.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为
.
20.如图是由边长为1的小正方形构成的网格.每个小正方形的顶点叫做格点.△ABC的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)将边AB绕点B逆时针旋转90°得到线段BA';
(2)画△ABC的高AD;
(3)将点D竖直向下平移3个单位长度得到点D',画出点D';
(4)画线段A'B关于直线BC的对称线段BA″.
21.在下面的正方形网格中按要求作图.
(1)在图①中将△ABC平移,使点A与点C重合,得到△CPQ;
(2)在图②中将△ABC绕点C逆时针旋转90°,得到△MNC;
(3)在图③中作△FGH,使其与△ABC关于线段DE对称.
22.已知△ABC是等边三角形,点P在BC的延长线上,以P为旋转中心,将线段PC逆时针旋转n°(0<n<180)得线段PQ,连接AP,BQ.
(1)如图1,若PC=AC,画出n=60时的图形,直接写出BQ和AP的数量及位置关系;
(2)当n=120时,若点M为线段BQ的中点,连接PM.判断MP和AP的数量关系,并证明.
23.如图,将△ABC绕点A按顺时针方向旋转一定角度得△ADE,点B的对应点D恰好落在BC边上.
(1)若∠B=65°,求∠CDE的度数.
(2)若∠BAC=90°,∠B=60°,AC=,求CD的长.
24.如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点.
25.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点B的对应点为E,点A的对应点D落在线段AB上,DE与BC相交于点F,连接BE.
(Ⅰ)求证:DC平分∠ADE;
(Ⅱ)试判断BE与AB的位置关系,并说明理由;
(Ⅲ)若BE=BD,求∠ABC的大小.(直接写出结果即可)
参考答案
1.解:∵将△ABC绕点A按逆时针方向旋转得到△A′B′C′,
∴AB=AB′,∠C′B′A=∠B,
∴∠AB′B=∠B,
∵∠B=50°,
∴∠C′B′A=∠AB′B=50°,
∴∠CB′C′=180°﹣∠C′B′A﹣∠AB′B=80°,
故选:C.
2.解:∵将△ABC绕点B按逆时针方向旋转40°,
∴AB=DB,∠ABD=∠CBE=40°,
∴∠BAD=∠BDA=70°,
∵AD∥BC,
∴∠DAB=∠ABC=70°,
∴∠ABE=∠ABC﹣∠EBC=30°,
故选:B.
3.解:∵△ABE的周长=AB+BE+AE=10(cm),由平移的性质可知,BC=AD=EF=1(cm),AE=DF,
∴四边形ABFD的周长=AB+BE+EF+DF+AD=10+1+1=12(cm).
故选:A.
4.解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;
B、既是轴对称图形,也是中心对称图形,故此选项符合题意;
C、不是轴对称图形,是中心对称图形,故此选项不合题意;
D、是轴对称图形,不是中心对称图形,故此选项不合题意.
故选:B.
5.解:在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,
这个正方形应该添加区域②处,
故选:B.
6.解:∵矩形长为10宽为5,
∴矩形的对角线长为:==5,
∵矩形在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,
∴该正方形的边长不小于5,
∵11<5<12,
∴该正方形边长的最小正数n为12.
故选:C.
7.解:∵将△ABC绕点A逆时针旋转150°,得到△ADE,
∴∠BAD=150°,AD=AB,∠E=∠ACB,
∵点B,C,D恰好在同一直线上,
∴△BAD是顶角为150°的等腰三角形,
∴∠B=∠BDA,
∴∠B=(180°﹣∠BAD)=15°,
∴∠E=∠ACB=180°﹣∠BAC﹣∠B=180°﹣100°﹣15°=65°,
故选:C.
8.解:将△ABC绕点A顺时针旋转,得到△ADE,
∴∠BAC=∠DAE,AB=AD,BC=DE,故A、B、D选项正确;
∵∠C=∠E,但∠C不一定等于∠DAE,
∴BC不一定平行于AE,故C选项,错误;
故选:C.
9.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故①错误,③正确;
∴∠ACD=∠BCE,
∴∠A=∠ADC=,∠CBE=,
∴∠A=∠EBC,故④正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故②错误.
故选:C.
10.解:在CB上取一点G使得CG=CD,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴△CDG是等边三角形,
∴CD=DG=CG,
∵∠BDG+∠EDG=60°,∠EDC+∠EDG=60°,
∴∠BDG=∠EDC,
在△BDG和△EDC中,
,
∴△BDG≌△EDC(SAS),
∴BG=CE,
∴BC=BG+CG=CE+CD=4,
解法二:证明△ABD≌△CBE(SAS),可得AD=EC=3,
∴BC=AC=AD+CD=3+1=4.
故选:C.
11.解:由题意,空白部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
∴阴影部分的面积=5×3×2﹣2×2×3=18(cm2),
故答案为:18.
12.解:正六边形可以被经过中心的射线平分成6个全等的部分,
则旋转至少360°÷6=60°,能够与本身重合.
故答案为:60°.
13.解:∵点(﹣m,n+3)与点(2,﹣2m)关于原点对称,
∴﹣m=﹣2,n+3=2m,
解得:m=2,n=1.
∴m+n=2+1=3.
故答案为:3.
14.解:过点D作DH∥CE交AB于点H,过点E作EG⊥CA的延长线于点G,
∵把AD绕点A逆时针旋转120°,得到AF,
∴∠DAF=120°,AD=AF,
∵∠BAC=∠DAF=120°,
∴∠DAH=∠CAF,
∵DH∥CE,
∴∠AEC=∠AHD,
∵∠AEC=∠ACF,
∴∠ACF=∠AHD,
在△ACF与△AHD中,
,
∴△ACF≌△AHD(AAS),
∴AC=AH,CF=DH=7,
设EH=x,
∴AH=AC=6+x,
∵∠BAC=120°,
∴∠EAG=60°,
∴AG=AE=3,
由勾股定理可知:EG==3,
∵点D是BC的中点,DH∥CE,
∴DH是△CBE的中位线,
∴CE=14,
在Rt△CEG中,CG2+EG2=CE2,
∴(6+x+3)2+(3)2=142,
∴x=4,
∴AC=x+6=4+6=10.
故答案为:10.
15.解:(1)∵∠BAC=40°,
∴∠BAD=140°,
∴△ABC旋转了140°,
故答案为:140;
(2)由旋转的性质可知,AC=AE,
∴△AEC是等腰三角形,
故答案为:等腰三角形;
(3)由旋转的性质可知,∠CAE=∠BAD=140°,又AC=AE,
∴∠AEC=(180°﹣140°)÷2=20°,
故答案为:20°.
16.解:∵△ABC是等边三角形,
∴BC=AB=12,
∵BC=3BD,
∴BD=BC=4,
由旋转的性质得:△ACE≌△ABD,
∴CE=BD=4.
故答案为:4.
17.解:设B′C′与CD交于点E,连接AE.
在Rt△AB′E与Rt△ADE中,∠AB′E=∠ADE=90°,
,
∴Rt△AB′E≌Rt△ADE(HL),
∴∠B′AE=∠DAE.
∵∠BAB′=30°,∠BAD=90°,
∴∠B′AE=∠DAE=30°,
∴DE=a.
∴S四边形AB′ED=2S△ADE=2××a×a=a2.
∴阴影部分的面积=S正方形ABCD﹣S四边形AB′ED=(1﹣)a2.
故答案为:(1﹣)a2.
18.解:依题意有3a﹣3×1=12,
解得a=5.
故答案为:5.
19.解:由旋转的性质可知:BC=DE=1,AB=AD,∠BAD=90°,
在Rt△ABC中,AC=3,BC=1,∠ACB=90°,
由勾股定理得:AB=AD===,
在Rt△ADB中,BD===2,
即:BD的长为2,
故答案为:2.
20.解:(1)如图,线段BA′即为所求作.
(2)如图,线段AD即为所求作.
(3)如图,点D′即为所求作.
(4)如图,线段BA″即为所求作.
21.解:(1)如图,△CPQ为所作;
(2)如图,△MNC为所作;
(3)如图,△FGH为所作.
22.解:(1)BQ=AP,BQ∥AP,
如图1所示:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
又∵PC=AC,
∴∠PAC=∠APC,
∵∠ACB=∠PAC+∠APC=60°,
∴∠PAC=∠APC=30°,
∴∠BAP=90°,
∵将线段PC逆时针旋转60°得线段PQ,
∴PC=PQ,∠CPQ=60°,
∴AB=AC=CP=PQ,∠APQ=90°,
∴∠BAP+∠APQ=180°,
∴AB∥PQ,
∴四边形ABQP是平行四边形,
∴BQ=AP,BQ∥AP;
(2)AP=2MP,
理由如下:如图2,以CP为边作等边三角形CHP,连接BH,
∵△CHP和△CBA都是等边三角形,
∴CB=CA,CP=CH,∠ACB=∠HCP=∠CPH=60°,
∴∠BCH=∠ACP,
在△ACP和△BCH中,
,
∴△ACP≌△BCH(SAS),
∴AP=BH,
∵将线段PC逆时针旋转120°得线段PQ,
∴CP=PQ,∠CPQ=120°,
∵∠CPH+∠CPQ=180°,
∴点H,点P,点Q三点共线,
∵BM=MQ,PQ=CP=HP,
∴BH=2MP,
∴AP=2MP.
23.解:(1)∵将△ABC绕点A按顺时针方向旋转一定角度得△ADE,∠B=65°,
∴AB=AD,∠B=∠ADE=65°,
∴∠B=∠ADB=65°,
∴∠CDE=180°﹣∠ADB﹣∠ADE=180﹣65°﹣65°=50°;
(2)∵直角△ABC中,AC=,∠B=60°,
又∵AD=AB,∠B=60°,
∴△ABD是等边三角形,
∴BD=AB=1,
∴CD=BC﹣BD=2﹣1=1.
24.(1)证明:∵线段AD绕点A逆时针旋转60°得到线段AE,
∴△ADE是等边三角形,
在等边△ABC和等边△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)证明:如图,过点C作CG∥BP交DF的延长线于点G.
∴∠G=∠BDF,
∵∠ADE=60°,∠ADB=90°,
∴∠BDF=30°,
∴∠G=30°,
由(1)可知,BD=CE,∠CEA=∠BDA,
∵AD⊥BP,
∴∠BDA=90°,
∴∠CEA=90°,
∵∠AED=60°,
∴∠CED=30°=∠G,
∴CE=CG,
∴BD=CG,
在△BDF和△CGF中,
,
∴△BDF≌△CGF(AAS),
∴BF=FC,
即F为BC的中点.
25.(Ⅰ)证明:∵△DCE是由△ACB旋转得到,
∴CA=CD,∠A=∠CDE,
∴∠A=∠CDA,
∴∠CDA=∠CDE,
∴CD平分∠ADE.
(Ⅱ)解:结论:BE⊥AB.
由旋转的性质可知,∠ACD=∠BCE,
∵CA=CD,CB=CE,
∴∠CAD=∠CDA=∠CBE=∠CEB,
∵∠ABC+∠CAB+∠ACD+∠DCB=180°,
∴∠ABC+∠CBE+∠DCB+∠BCE=180°,
∴∠DCE+∠DBE=180°,
∵∠DCE=90°,
∴∠DBE=90°,
∴BE⊥AB.
(Ⅲ)如图,设BC交DE于O.连接AO,过点B作BH⊥CD交CD的延长线于H,作BT⊥CE于T,
∵∠H=∠BTC=∠HCT=90°,
∴∠HBT=∠DBE=90°,
∴∠DBH=∠EBT,
∵BD=BE,∠H=∠BTE=90°
∴△BHD≌△BTE(AAS),
∴BH=BT,
∵BH⊥CH,BT⊥CE,
∴∠DCO=∠DEB=45°,
∵∠ACB=90°,
∴∠ACD=∠OCD,
∵CD=CD,∠ADC=∠ODC,
∴△ACD≌△OCD(ASA),
∴AC=OC,
∴∠AOC=∠CAO=45°,
∵∠ADO=135°,
∴∠CAD=∠ADC=67.5°,
∴∠ABC=22.5°,
∵∠AOC=∠OAB+∠ABO,
∴∠OAB=∠ABO=22.5°
1.如图,在△ABC中,∠B=50°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,则∠CB′C′的度数为( )
A.50°
B.60°
C.80°
D.100°
2.如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD,若AD∥BC,则∠ABE的度数为( )
A.25°
B.30°
C.35°
D.40°
3.如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE的周长是10cm,那么四边形ABFD的周长是( )
A.12cm
B.16cm
C.18cm
D.20cm
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
5.图中阴影部分是由4个完全相同的的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在( )
A.区域①处
B.区域②处
C.区域③处
D.区域④处
6.如图,平面内某正方形内有一长为10宽为5的矩形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10
B.11
C.12
D.13
7.如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50°
B.75°
C.65°
D.60°
8.如图,将△ABC绕点A顺时针旋转,得到△ADE,且点D在AC上,下列说法错误的是( )
A.AC平分∠BAE
B.AB=AD
C.BC∥AE
D.BC=DE
9.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列四个结论:
①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC;
其中一定正确的是( )
A.①②
B.②③
C.③④
D.②③④
10.如图,△ABC是等边三角形,点D为AC边上一点,以BD为边作等边△BDE,连接CE.若CD=1,CE=3,则BC=( )
A.2
B.3
C.4
D.5
11.如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为
cm2.
12.正六边形绕其中心旋转一定的角度与原图形重合,则这个旋转角至少为
.
13.若点(﹣m,n+3)与点(2,﹣2m)关于原点对称,则m+n=
.
14.在△ABC中,∠BAC=120°,D为BC的中点,AE=6,把AD绕点A逆时针旋转120°,得到AF,若CF=7,∠ACF=∠AEC,则AC=
.
15.如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.
(1)△ABC旋转了
度.
(2)连接CE,判断△AEC的形状是
.
(3)若∠ACE=20°,则∠AEC的度数为
.
16.如图,在等边△ABC中,AB=12,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为
.
17.如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A'B'C'D',图中阴影部分的面积为
.
18.如图,有一块长为a米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草地的面积为12米2,则a=
.
19.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为
.
20.如图是由边长为1的小正方形构成的网格.每个小正方形的顶点叫做格点.△ABC的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)将边AB绕点B逆时针旋转90°得到线段BA';
(2)画△ABC的高AD;
(3)将点D竖直向下平移3个单位长度得到点D',画出点D';
(4)画线段A'B关于直线BC的对称线段BA″.
21.在下面的正方形网格中按要求作图.
(1)在图①中将△ABC平移,使点A与点C重合,得到△CPQ;
(2)在图②中将△ABC绕点C逆时针旋转90°,得到△MNC;
(3)在图③中作△FGH,使其与△ABC关于线段DE对称.
22.已知△ABC是等边三角形,点P在BC的延长线上,以P为旋转中心,将线段PC逆时针旋转n°(0<n<180)得线段PQ,连接AP,BQ.
(1)如图1,若PC=AC,画出n=60时的图形,直接写出BQ和AP的数量及位置关系;
(2)当n=120时,若点M为线段BQ的中点,连接PM.判断MP和AP的数量关系,并证明.
23.如图,将△ABC绕点A按顺时针方向旋转一定角度得△ADE,点B的对应点D恰好落在BC边上.
(1)若∠B=65°,求∠CDE的度数.
(2)若∠BAC=90°,∠B=60°,AC=,求CD的长.
24.如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点.
25.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点B的对应点为E,点A的对应点D落在线段AB上,DE与BC相交于点F,连接BE.
(Ⅰ)求证:DC平分∠ADE;
(Ⅱ)试判断BE与AB的位置关系,并说明理由;
(Ⅲ)若BE=BD,求∠ABC的大小.(直接写出结果即可)
参考答案
1.解:∵将△ABC绕点A按逆时针方向旋转得到△A′B′C′,
∴AB=AB′,∠C′B′A=∠B,
∴∠AB′B=∠B,
∵∠B=50°,
∴∠C′B′A=∠AB′B=50°,
∴∠CB′C′=180°﹣∠C′B′A﹣∠AB′B=80°,
故选:C.
2.解:∵将△ABC绕点B按逆时针方向旋转40°,
∴AB=DB,∠ABD=∠CBE=40°,
∴∠BAD=∠BDA=70°,
∵AD∥BC,
∴∠DAB=∠ABC=70°,
∴∠ABE=∠ABC﹣∠EBC=30°,
故选:B.
3.解:∵△ABE的周长=AB+BE+AE=10(cm),由平移的性质可知,BC=AD=EF=1(cm),AE=DF,
∴四边形ABFD的周长=AB+BE+EF+DF+AD=10+1+1=12(cm).
故选:A.
4.解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;
B、既是轴对称图形,也是中心对称图形,故此选项符合题意;
C、不是轴对称图形,是中心对称图形,故此选项不合题意;
D、是轴对称图形,不是中心对称图形,故此选项不合题意.
故选:B.
5.解:在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,
这个正方形应该添加区域②处,
故选:B.
6.解:∵矩形长为10宽为5,
∴矩形的对角线长为:==5,
∵矩形在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,
∴该正方形的边长不小于5,
∵11<5<12,
∴该正方形边长的最小正数n为12.
故选:C.
7.解:∵将△ABC绕点A逆时针旋转150°,得到△ADE,
∴∠BAD=150°,AD=AB,∠E=∠ACB,
∵点B,C,D恰好在同一直线上,
∴△BAD是顶角为150°的等腰三角形,
∴∠B=∠BDA,
∴∠B=(180°﹣∠BAD)=15°,
∴∠E=∠ACB=180°﹣∠BAC﹣∠B=180°﹣100°﹣15°=65°,
故选:C.
8.解:将△ABC绕点A顺时针旋转,得到△ADE,
∴∠BAC=∠DAE,AB=AD,BC=DE,故A、B、D选项正确;
∵∠C=∠E,但∠C不一定等于∠DAE,
∴BC不一定平行于AE,故C选项,错误;
故选:C.
9.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故①错误,③正确;
∴∠ACD=∠BCE,
∴∠A=∠ADC=,∠CBE=,
∴∠A=∠EBC,故④正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故②错误.
故选:C.
10.解:在CB上取一点G使得CG=CD,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴△CDG是等边三角形,
∴CD=DG=CG,
∵∠BDG+∠EDG=60°,∠EDC+∠EDG=60°,
∴∠BDG=∠EDC,
在△BDG和△EDC中,
,
∴△BDG≌△EDC(SAS),
∴BG=CE,
∴BC=BG+CG=CE+CD=4,
解法二:证明△ABD≌△CBE(SAS),可得AD=EC=3,
∴BC=AC=AD+CD=3+1=4.
故选:C.
11.解:由题意,空白部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
∴阴影部分的面积=5×3×2﹣2×2×3=18(cm2),
故答案为:18.
12.解:正六边形可以被经过中心的射线平分成6个全等的部分,
则旋转至少360°÷6=60°,能够与本身重合.
故答案为:60°.
13.解:∵点(﹣m,n+3)与点(2,﹣2m)关于原点对称,
∴﹣m=﹣2,n+3=2m,
解得:m=2,n=1.
∴m+n=2+1=3.
故答案为:3.
14.解:过点D作DH∥CE交AB于点H,过点E作EG⊥CA的延长线于点G,
∵把AD绕点A逆时针旋转120°,得到AF,
∴∠DAF=120°,AD=AF,
∵∠BAC=∠DAF=120°,
∴∠DAH=∠CAF,
∵DH∥CE,
∴∠AEC=∠AHD,
∵∠AEC=∠ACF,
∴∠ACF=∠AHD,
在△ACF与△AHD中,
,
∴△ACF≌△AHD(AAS),
∴AC=AH,CF=DH=7,
设EH=x,
∴AH=AC=6+x,
∵∠BAC=120°,
∴∠EAG=60°,
∴AG=AE=3,
由勾股定理可知:EG==3,
∵点D是BC的中点,DH∥CE,
∴DH是△CBE的中位线,
∴CE=14,
在Rt△CEG中,CG2+EG2=CE2,
∴(6+x+3)2+(3)2=142,
∴x=4,
∴AC=x+6=4+6=10.
故答案为:10.
15.解:(1)∵∠BAC=40°,
∴∠BAD=140°,
∴△ABC旋转了140°,
故答案为:140;
(2)由旋转的性质可知,AC=AE,
∴△AEC是等腰三角形,
故答案为:等腰三角形;
(3)由旋转的性质可知,∠CAE=∠BAD=140°,又AC=AE,
∴∠AEC=(180°﹣140°)÷2=20°,
故答案为:20°.
16.解:∵△ABC是等边三角形,
∴BC=AB=12,
∵BC=3BD,
∴BD=BC=4,
由旋转的性质得:△ACE≌△ABD,
∴CE=BD=4.
故答案为:4.
17.解:设B′C′与CD交于点E,连接AE.
在Rt△AB′E与Rt△ADE中,∠AB′E=∠ADE=90°,
,
∴Rt△AB′E≌Rt△ADE(HL),
∴∠B′AE=∠DAE.
∵∠BAB′=30°,∠BAD=90°,
∴∠B′AE=∠DAE=30°,
∴DE=a.
∴S四边形AB′ED=2S△ADE=2××a×a=a2.
∴阴影部分的面积=S正方形ABCD﹣S四边形AB′ED=(1﹣)a2.
故答案为:(1﹣)a2.
18.解:依题意有3a﹣3×1=12,
解得a=5.
故答案为:5.
19.解:由旋转的性质可知:BC=DE=1,AB=AD,∠BAD=90°,
在Rt△ABC中,AC=3,BC=1,∠ACB=90°,
由勾股定理得:AB=AD===,
在Rt△ADB中,BD===2,
即:BD的长为2,
故答案为:2.
20.解:(1)如图,线段BA′即为所求作.
(2)如图,线段AD即为所求作.
(3)如图,点D′即为所求作.
(4)如图,线段BA″即为所求作.
21.解:(1)如图,△CPQ为所作;
(2)如图,△MNC为所作;
(3)如图,△FGH为所作.
22.解:(1)BQ=AP,BQ∥AP,
如图1所示:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
又∵PC=AC,
∴∠PAC=∠APC,
∵∠ACB=∠PAC+∠APC=60°,
∴∠PAC=∠APC=30°,
∴∠BAP=90°,
∵将线段PC逆时针旋转60°得线段PQ,
∴PC=PQ,∠CPQ=60°,
∴AB=AC=CP=PQ,∠APQ=90°,
∴∠BAP+∠APQ=180°,
∴AB∥PQ,
∴四边形ABQP是平行四边形,
∴BQ=AP,BQ∥AP;
(2)AP=2MP,
理由如下:如图2,以CP为边作等边三角形CHP,连接BH,
∵△CHP和△CBA都是等边三角形,
∴CB=CA,CP=CH,∠ACB=∠HCP=∠CPH=60°,
∴∠BCH=∠ACP,
在△ACP和△BCH中,
,
∴△ACP≌△BCH(SAS),
∴AP=BH,
∵将线段PC逆时针旋转120°得线段PQ,
∴CP=PQ,∠CPQ=120°,
∵∠CPH+∠CPQ=180°,
∴点H,点P,点Q三点共线,
∵BM=MQ,PQ=CP=HP,
∴BH=2MP,
∴AP=2MP.
23.解:(1)∵将△ABC绕点A按顺时针方向旋转一定角度得△ADE,∠B=65°,
∴AB=AD,∠B=∠ADE=65°,
∴∠B=∠ADB=65°,
∴∠CDE=180°﹣∠ADB﹣∠ADE=180﹣65°﹣65°=50°;
(2)∵直角△ABC中,AC=,∠B=60°,
又∵AD=AB,∠B=60°,
∴△ABD是等边三角形,
∴BD=AB=1,
∴CD=BC﹣BD=2﹣1=1.
24.(1)证明:∵线段AD绕点A逆时针旋转60°得到线段AE,
∴△ADE是等边三角形,
在等边△ABC和等边△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)证明:如图,过点C作CG∥BP交DF的延长线于点G.
∴∠G=∠BDF,
∵∠ADE=60°,∠ADB=90°,
∴∠BDF=30°,
∴∠G=30°,
由(1)可知,BD=CE,∠CEA=∠BDA,
∵AD⊥BP,
∴∠BDA=90°,
∴∠CEA=90°,
∵∠AED=60°,
∴∠CED=30°=∠G,
∴CE=CG,
∴BD=CG,
在△BDF和△CGF中,
,
∴△BDF≌△CGF(AAS),
∴BF=FC,
即F为BC的中点.
25.(Ⅰ)证明:∵△DCE是由△ACB旋转得到,
∴CA=CD,∠A=∠CDE,
∴∠A=∠CDA,
∴∠CDA=∠CDE,
∴CD平分∠ADE.
(Ⅱ)解:结论:BE⊥AB.
由旋转的性质可知,∠ACD=∠BCE,
∵CA=CD,CB=CE,
∴∠CAD=∠CDA=∠CBE=∠CEB,
∵∠ABC+∠CAB+∠ACD+∠DCB=180°,
∴∠ABC+∠CBE+∠DCB+∠BCE=180°,
∴∠DCE+∠DBE=180°,
∵∠DCE=90°,
∴∠DBE=90°,
∴BE⊥AB.
(Ⅲ)如图,设BC交DE于O.连接AO,过点B作BH⊥CD交CD的延长线于H,作BT⊥CE于T,
∵∠H=∠BTC=∠HCT=90°,
∴∠HBT=∠DBE=90°,
∴∠DBH=∠EBT,
∵BD=BE,∠H=∠BTE=90°
∴△BHD≌△BTE(AAS),
∴BH=BT,
∵BH⊥CH,BT⊥CE,
∴∠DCO=∠DEB=45°,
∵∠ACB=90°,
∴∠ACD=∠OCD,
∵CD=CD,∠ADC=∠ODC,
∴△ACD≌△OCD(ASA),
∴AC=OC,
∴∠AOC=∠CAO=45°,
∵∠ADO=135°,
∴∠CAD=∠ADC=67.5°,
∴∠ABC=22.5°,
∵∠AOC=∠OAB+∠ABO,
∴∠OAB=∠ABO=22.5°
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
