人教版数学八年级下册 平行四边形的性质与判定(要点梳理+专项冲刺) (word版含答案)
文档属性
| 名称 | 人教版数学八年级下册 平行四边形的性质与判定(要点梳理+专项冲刺) (word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 908.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览


文档简介
平行四边形的性质与判定
要点梳理+专项冲刺
要点梳理
要点一、平行四边形的定义
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
平行四边形ABCD记作“ABCD”,读作“平行四边形ABCD”.
要点诠释:
平行四边形的基本元素:边、角、对角线.相邻的两边为邻边,有四对;
相对的边为对边,有两对;
相邻的两角为邻角,有四对;
相对的角为对角,有两对;
对角线有两条.
要点二、平行四边形的性质
1.边的性质:平行四边形两组对边平行且相等;
2.角的性质:平行四边形对角相等,邻角互补;
3.对角线性质:平行四边形的对角线互相平分;
4.平行四边形是中心对称图形,对角线的交点为对称中心;
要点诠释:(1)平行四边形的性质中边的性质可以证明两边平行或两边相等;角的性质可以证明两角相等或两角互补;对角线的性质可以证明线段的相等关系或倍半关系.
(2)由于平行四边形的性质内容较多,在使用时根据需要进行选择.
(3)利用对角线互相平分可解决对角线或边的取值范围的问题,在解答时应联系三角形三边的不等关系来解决.
要点三、平行线间的距离
1.两条平行线间的距离:
(1)定义:两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线间的距离.注:距离是指垂线段的长度,是正值.
(2)平行线间的距离处处相等
任何两平行线间的距离都是存在的、唯一的,都是夹在这两条平行线间最短的线段的长度.
两条平行线间的任何两条平行线段都是相等的.
2.平行四边形的面积:
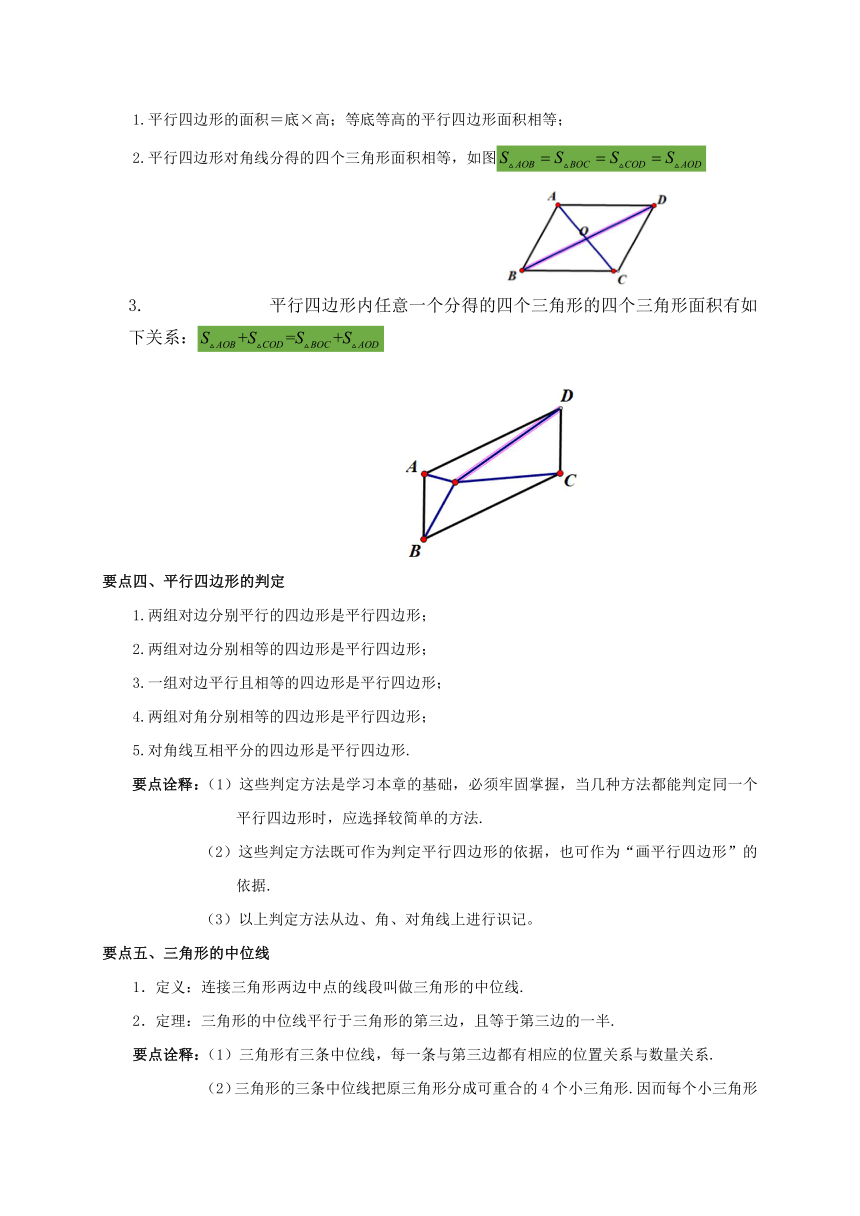
1.平行四边形的面积=底×高;等底等高的平行四边形面积相等;
2.平行四边形对角线分得的四个三角形面积相等,如图
平行四边形内任意一个分得的四个三角形的四个三角形面积有如下关系:
要点四、平行四边形的判定
1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.一组对边平行且相等的四边形是平行四边形;
4.两组对角分别相等的四边形是平行四边形;
5.对角线互相平分的四边形是平行四边形.
要点诠释:(1)这些判定方法是学习本章的基础,必须牢固掌握,当几种方法都能判定同一个平行四边形时,应选择较简单的方法.
这些判定方法既可作为判定平行四边形的依据,也可作为“画平行四边形”的依据.
以上判定方法从边、角、对角线上进行识记。
要点五、三角形的中位线
1.定义:连接三角形两边中点的线段叫做三角形的中位线.
2.定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.
(2)三角形的三条中位线把原三角形分成可重合的4个小三角形.因而每个小三角形的周长为原三角形周长的,每个小三角形的面积为原三角形面积的.
(3)三角形的中位线不同于三角形的中线.
专项冲刺
选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的)
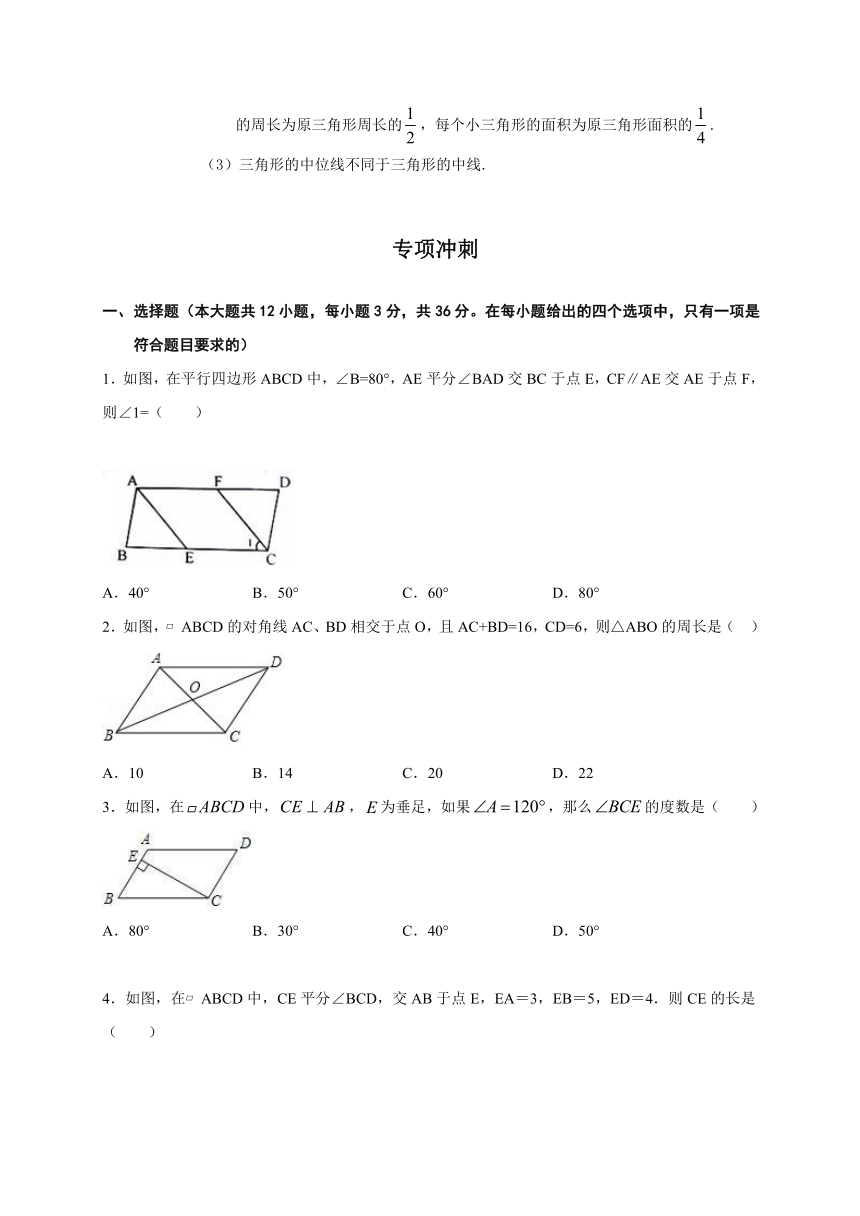
1.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A.40°
B.50°
C.60°
D.80°
2.如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是(
)
A.10
B.14
C.20
D.22
3.如图,在中,,为垂足,如果,那么的度数是(
)
A.80°
B.30°
C.40°
D.50°
4.如图,在?ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5
B.6
C.4
D.5
5.如图,在平行四边形中,,是锐角,于点,是的中点,连接;若,则的长为(
)
A.
B.
C.
D.
6.如图,四边形是平行四边形,点E,B,D,F在同一条直线上,请添加一个条件使得,下列不正确的是(
)
A.
B.
C.
D.
7.一个零件的形状如图所示,,则的度数是(
)
A.70°
B.80°
C.90°
D.100°
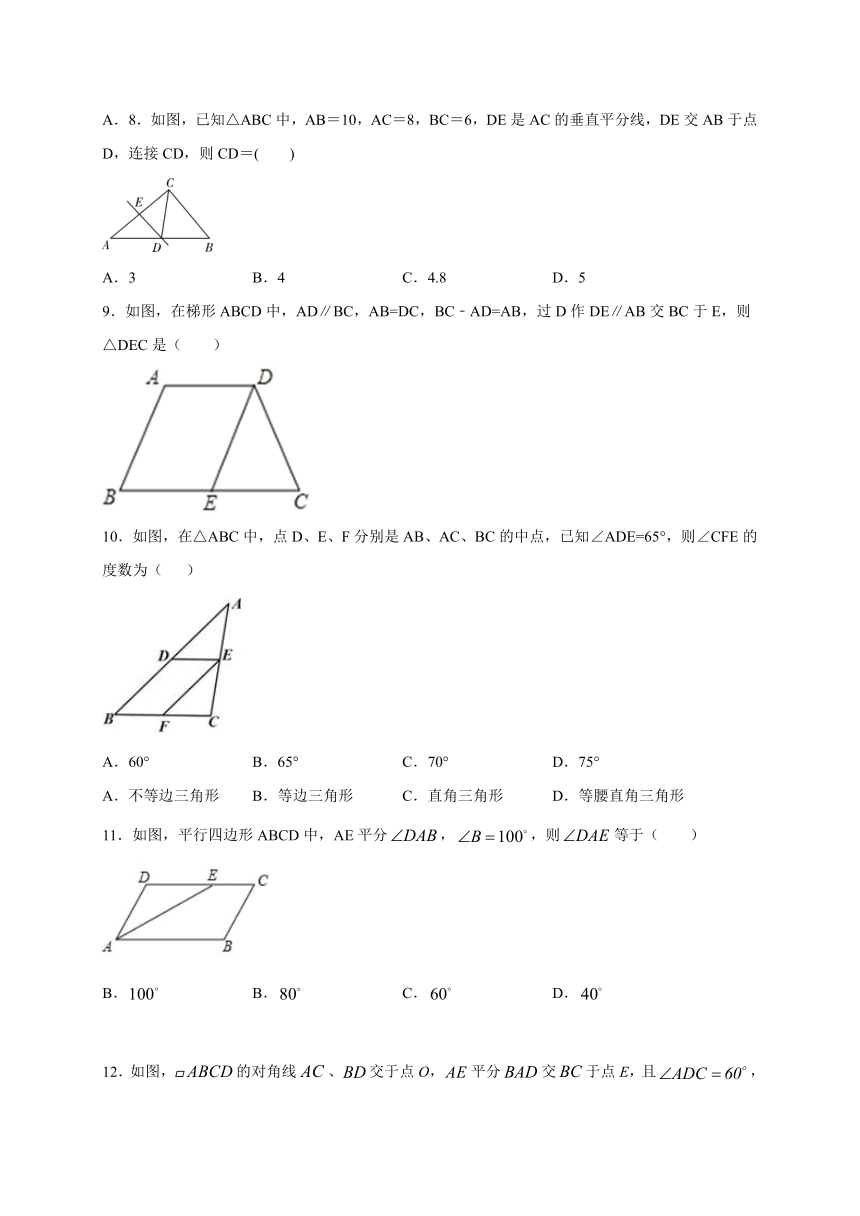
8.如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD=( )
A.3
B.4
C.4.8
D.5
9.如图,在梯形ABCD中,AD∥BC,AB=DC,BC﹣AD=AB,过D作DE∥AB交BC于E,则△DEC是(
)
10.如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,已知∠ADE=65°,则∠CFE的度数为(
)
A.60°
B.65°
C.70°
D.75°
A.不等边三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
11.如图,平行四边形ABCD中,AE平分,,则等于(
)
B.
C.
D.
12.如图,的对角线、交于点O,平分交于点E,且,,连接.下列结论:①;②;③;④;成立的个数有(
)
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共6小题,每小题3分,共18分)
13.如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
14.点是平行四边形的对称中心,,、分别是边上的点,且;、分别是边上的点,且;若,分别表示和的面积,则,之间的等量关系是__________.
15.如图,在中,平分,于点,交BC于点F,点是的中点,若,,则的长为______.
16.如图,平面直角坐标系中,点A(4,3),点B(3,0),点C(5,3),∠OAB沿AC方向平移AC长度的到∠ECF,四边形ABFC的面积为_________.
17.如图,将沿对角线进行折叠,折叠后点D落在点F处,交于点E,有下列结论:①;②;③;④,其中正确结论的是__________.
18.在△ABC中,
AD是BC边上的高线,CE
是AB边上的中线,CD=AE,且CE三、解答题(本大题共6小题,共66分,解答应写出文字说明、演算步骤或推理过程)
19.如图,点在外,连接,,延长交于,为的中点.
(1)求证:;
(2)若,,,,求的长.
20.如图,在□
ABCD中,点P在对角线AC上一动点,过点P作PM//DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证:
△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
21.已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在对角线AC上,且BF=DE,AH=CG,连接FH、HE、BG、FG.
(1)求证:FG=EH.
(2)若EG平分∠AEH,FH平分∠CFG,FG//AB,∠ACD=68°,∠GFH=35°,求∠GHF的度数.
22.如图,的对角线、交于点,,分别是、的中点.
(1)求证:四边形是平行四边形;
(2)若,,,求的长度.
23.如图,在平行四边形ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.
(1)求证:AEF≌DEC;
(2)求证:四边形ACDF是平行四边形.
24.如图1,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过点O作MN∥BC.分别交AB、AC于M、N.
(1)求证:BM+CN=MN.
(2)如图2,若△ABC是等边三角形,请从以下两个问题任选一题作答.若两题都作答,以问题①计分.
问题①BC=6,求MN的长.
问题②求证:O是MN的中点.
【答案】
选择题
1-5
BBBCB
6-10
ABDBB
11-12
DB
填空题
13.48
14.
15.1.5
16.3
17.①②③
18.
解答题
19.(1)见解析;(2)
解:(1)连接交于点,
∵四边形是平行四边形,
∴,
∵,
∴OF为△DBE的中位线
∴.
(2)∵AD=2,∠ACD=90°,∠ADC=60°,
∴.
∵是的中位线,
∴.
∴.
∵,
∴.
20.(1)证明见解析;(2)
【分析】
(1)根据四边形ABCD是平行四边形,得到AD=BC,∠ADC+∠BCD=,由PM//DC,且PM=DC,证得四边形PMCD是平行四边形,得到PD=CM,∠PDC+∠DCM=,推出∠ADP=∠BCM,即可证得结论;
(2)作BH⊥AC于H,DG⊥AC于G,根据四边形ABCD是平行四边形,得到△ABC≌△CDA,BH=DG,求得,,利用△ADP≌△BCM,得到,即可求出答案.
【解析】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADC+∠BCD=,
∵PM//DC,且PM=DC,
∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM=,
∴∠ADP=∠BCM,
∴△ADP≌△BCM;
(2)解:作BH⊥AC于H,DG⊥AC于G,
∵四边形ABCD是平行四边形,
∴△ABC≌△CDA,
∴BH=DG,
∴,即,
,即,
∵△ADP≌△BCM,
∴,
∴=.
21.(1)证明见解析;(2)77°
【解析】
解:(1)∵四边形ABCD是平行四边形,
∴,,
∴,
∵,
∴,即,
在和中,
,
∴≌,
∴FG=EH;
(2)∵FH平分∠CFG,∠GFH=35°,
∴,
∵FG//AB,
∴,
∵四边形ABCD是平行四边形,
∴,
∴,
∴.
22.(1)∵四边形是平行四边形,
∴AO=OC,BO=OD.
∵,分别是、的中点,
∴,,
∴,,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴,.
∵,,
∴,.
∵,
∴
∵是的中点,,
∴,
∴.
23.(1)∵在平行四边形ABCD中,AB∥CD,
∴∠FAE=∠CDE,
∵点E是边AD的中点,
∴AE=DE,
在△AEF和△DEC中,
∴△AEF≌△DEC(ASA).
(2)∵△AEF≌△DEC,
∴AF=DC,
∵AF∥DC,
∴四边形ACDF是平行四边形.
24.(1)证明:∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠MBO,∠OCB=∠NCO,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MOB=∠MBO,∠NOC=∠NCO,
∴BM=MO,CN=ON,
∴BM+CN=MO+ON=MN,
即BM+CN
=MN;
(2)若选①,解:如图2,过M、N分别作ME⊥BC于E,NF⊥BC于F,
则ME∥NF,∠MEB=∠NFC=90°,
∵MN∥BC,
∴四边形MEFN为平行四边形,
∴MN=EF,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,又∠MEB=∠NFC=90°,
∴∠BME=∠CNF=30°,
∴BE=BM,CF=CN,
∵BC=BE+EF+CF=BM+MN+CN=MN=6,
∴MN=4;
若选②,证明:如图2,过M、N分别作ME⊥BC于E,NF⊥BC于F,
则ME∥NF,∠MEB=∠NFC=90°
∵MN∥BC,
∴四边形MEFN为平行四边形,
∴ME=NF,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
又∠MEB=∠NFC=90°,
∴△MEB≌△NFC(AAS),
∴BM=CN,
∵
BM=MO,CN=ON
∴MO=ON,
即O为MN的中点.
要点梳理+专项冲刺
要点梳理
要点一、平行四边形的定义
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
平行四边形ABCD记作“ABCD”,读作“平行四边形ABCD”.
要点诠释:
平行四边形的基本元素:边、角、对角线.相邻的两边为邻边,有四对;
相对的边为对边,有两对;
相邻的两角为邻角,有四对;
相对的角为对角,有两对;
对角线有两条.
要点二、平行四边形的性质
1.边的性质:平行四边形两组对边平行且相等;
2.角的性质:平行四边形对角相等,邻角互补;
3.对角线性质:平行四边形的对角线互相平分;
4.平行四边形是中心对称图形,对角线的交点为对称中心;
要点诠释:(1)平行四边形的性质中边的性质可以证明两边平行或两边相等;角的性质可以证明两角相等或两角互补;对角线的性质可以证明线段的相等关系或倍半关系.
(2)由于平行四边形的性质内容较多,在使用时根据需要进行选择.
(3)利用对角线互相平分可解决对角线或边的取值范围的问题,在解答时应联系三角形三边的不等关系来解决.
要点三、平行线间的距离
1.两条平行线间的距离:
(1)定义:两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线间的距离.注:距离是指垂线段的长度,是正值.
(2)平行线间的距离处处相等
任何两平行线间的距离都是存在的、唯一的,都是夹在这两条平行线间最短的线段的长度.
两条平行线间的任何两条平行线段都是相等的.
2.平行四边形的面积:
1.平行四边形的面积=底×高;等底等高的平行四边形面积相等;
2.平行四边形对角线分得的四个三角形面积相等,如图
平行四边形内任意一个分得的四个三角形的四个三角形面积有如下关系:
要点四、平行四边形的判定
1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.一组对边平行且相等的四边形是平行四边形;
4.两组对角分别相等的四边形是平行四边形;
5.对角线互相平分的四边形是平行四边形.
要点诠释:(1)这些判定方法是学习本章的基础,必须牢固掌握,当几种方法都能判定同一个平行四边形时,应选择较简单的方法.
这些判定方法既可作为判定平行四边形的依据,也可作为“画平行四边形”的依据.
以上判定方法从边、角、对角线上进行识记。
要点五、三角形的中位线
1.定义:连接三角形两边中点的线段叫做三角形的中位线.
2.定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.
(2)三角形的三条中位线把原三角形分成可重合的4个小三角形.因而每个小三角形的周长为原三角形周长的,每个小三角形的面积为原三角形面积的.
(3)三角形的中位线不同于三角形的中线.
专项冲刺
选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A.40°
B.50°
C.60°
D.80°
2.如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是(
)
A.10
B.14
C.20
D.22
3.如图,在中,,为垂足,如果,那么的度数是(
)
A.80°
B.30°
C.40°
D.50°
4.如图,在?ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5
B.6
C.4
D.5
5.如图,在平行四边形中,,是锐角,于点,是的中点,连接;若,则的长为(
)
A.
B.
C.
D.
6.如图,四边形是平行四边形,点E,B,D,F在同一条直线上,请添加一个条件使得,下列不正确的是(
)
A.
B.
C.
D.
7.一个零件的形状如图所示,,则的度数是(
)
A.70°
B.80°
C.90°
D.100°
8.如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD=( )
A.3
B.4
C.4.8
D.5
9.如图,在梯形ABCD中,AD∥BC,AB=DC,BC﹣AD=AB,过D作DE∥AB交BC于E,则△DEC是(
)
10.如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,已知∠ADE=65°,则∠CFE的度数为(
)
A.60°
B.65°
C.70°
D.75°
A.不等边三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
11.如图,平行四边形ABCD中,AE平分,,则等于(
)
B.
C.
D.
12.如图,的对角线、交于点O,平分交于点E,且,,连接.下列结论:①;②;③;④;成立的个数有(
)
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共6小题,每小题3分,共18分)
13.如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
14.点是平行四边形的对称中心,,、分别是边上的点,且;、分别是边上的点,且;若,分别表示和的面积,则,之间的等量关系是__________.
15.如图,在中,平分,于点,交BC于点F,点是的中点,若,,则的长为______.
16.如图,平面直角坐标系中,点A(4,3),点B(3,0),点C(5,3),∠OAB沿AC方向平移AC长度的到∠ECF,四边形ABFC的面积为_________.
17.如图,将沿对角线进行折叠,折叠后点D落在点F处,交于点E,有下列结论:①;②;③;④,其中正确结论的是__________.
18.在△ABC中,
AD是BC边上的高线,CE
是AB边上的中线,CD=AE,且CE
19.如图,点在外,连接,,延长交于,为的中点.
(1)求证:;
(2)若,,,,求的长.
20.如图,在□
ABCD中,点P在对角线AC上一动点,过点P作PM//DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证:
△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
21.已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在对角线AC上,且BF=DE,AH=CG,连接FH、HE、BG、FG.
(1)求证:FG=EH.
(2)若EG平分∠AEH,FH平分∠CFG,FG//AB,∠ACD=68°,∠GFH=35°,求∠GHF的度数.
22.如图,的对角线、交于点,,分别是、的中点.
(1)求证:四边形是平行四边形;
(2)若,,,求的长度.
23.如图,在平行四边形ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.
(1)求证:AEF≌DEC;
(2)求证:四边形ACDF是平行四边形.
24.如图1,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过点O作MN∥BC.分别交AB、AC于M、N.
(1)求证:BM+CN=MN.
(2)如图2,若△ABC是等边三角形,请从以下两个问题任选一题作答.若两题都作答,以问题①计分.
问题①BC=6,求MN的长.
问题②求证:O是MN的中点.
【答案】
选择题
1-5
BBBCB
6-10
ABDBB
11-12
DB
填空题
13.48
14.
15.1.5
16.3
17.①②③
18.
解答题
19.(1)见解析;(2)
解:(1)连接交于点,
∵四边形是平行四边形,
∴,
∵,
∴OF为△DBE的中位线
∴.
(2)∵AD=2,∠ACD=90°,∠ADC=60°,
∴.
∵是的中位线,
∴.
∴.
∵,
∴.
20.(1)证明见解析;(2)
【分析】
(1)根据四边形ABCD是平行四边形,得到AD=BC,∠ADC+∠BCD=,由PM//DC,且PM=DC,证得四边形PMCD是平行四边形,得到PD=CM,∠PDC+∠DCM=,推出∠ADP=∠BCM,即可证得结论;
(2)作BH⊥AC于H,DG⊥AC于G,根据四边形ABCD是平行四边形,得到△ABC≌△CDA,BH=DG,求得,,利用△ADP≌△BCM,得到,即可求出答案.
【解析】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADC+∠BCD=,
∵PM//DC,且PM=DC,
∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM=,
∴∠ADP=∠BCM,
∴△ADP≌△BCM;
(2)解:作BH⊥AC于H,DG⊥AC于G,
∵四边形ABCD是平行四边形,
∴△ABC≌△CDA,
∴BH=DG,
∴,即,
,即,
∵△ADP≌△BCM,
∴,
∴=.
21.(1)证明见解析;(2)77°
【解析】
解:(1)∵四边形ABCD是平行四边形,
∴,,
∴,
∵,
∴,即,
在和中,
,
∴≌,
∴FG=EH;
(2)∵FH平分∠CFG,∠GFH=35°,
∴,
∵FG//AB,
∴,
∵四边形ABCD是平行四边形,
∴,
∴,
∴.
22.(1)∵四边形是平行四边形,
∴AO=OC,BO=OD.
∵,分别是、的中点,
∴,,
∴,,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴,.
∵,,
∴,.
∵,
∴
∵是的中点,,
∴,
∴.
23.(1)∵在平行四边形ABCD中,AB∥CD,
∴∠FAE=∠CDE,
∵点E是边AD的中点,
∴AE=DE,
在△AEF和△DEC中,
∴△AEF≌△DEC(ASA).
(2)∵△AEF≌△DEC,
∴AF=DC,
∵AF∥DC,
∴四边形ACDF是平行四边形.
24.(1)证明:∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠MBO,∠OCB=∠NCO,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MOB=∠MBO,∠NOC=∠NCO,
∴BM=MO,CN=ON,
∴BM+CN=MO+ON=MN,
即BM+CN
=MN;
(2)若选①,解:如图2,过M、N分别作ME⊥BC于E,NF⊥BC于F,
则ME∥NF,∠MEB=∠NFC=90°,
∵MN∥BC,
∴四边形MEFN为平行四边形,
∴MN=EF,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,又∠MEB=∠NFC=90°,
∴∠BME=∠CNF=30°,
∴BE=BM,CF=CN,
∵BC=BE+EF+CF=BM+MN+CN=MN=6,
∴MN=4;
若选②,证明:如图2,过M、N分别作ME⊥BC于E,NF⊥BC于F,
则ME∥NF,∠MEB=∠NFC=90°
∵MN∥BC,
∴四边形MEFN为平行四边形,
∴ME=NF,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
又∠MEB=∠NFC=90°,
∴△MEB≌△NFC(AAS),
∴BM=CN,
∵
BM=MO,CN=ON
∴MO=ON,
即O为MN的中点.
