2020-2021学年八年级数学人教版下册:17.1应用勾股定理求常见几何体的最短路线的长(表格式教案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册:17.1应用勾股定理求常见几何体的最短路线的长(表格式教案) |
|
|
| 格式 | zip | ||
| 文件大小 | 25.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览

文档简介
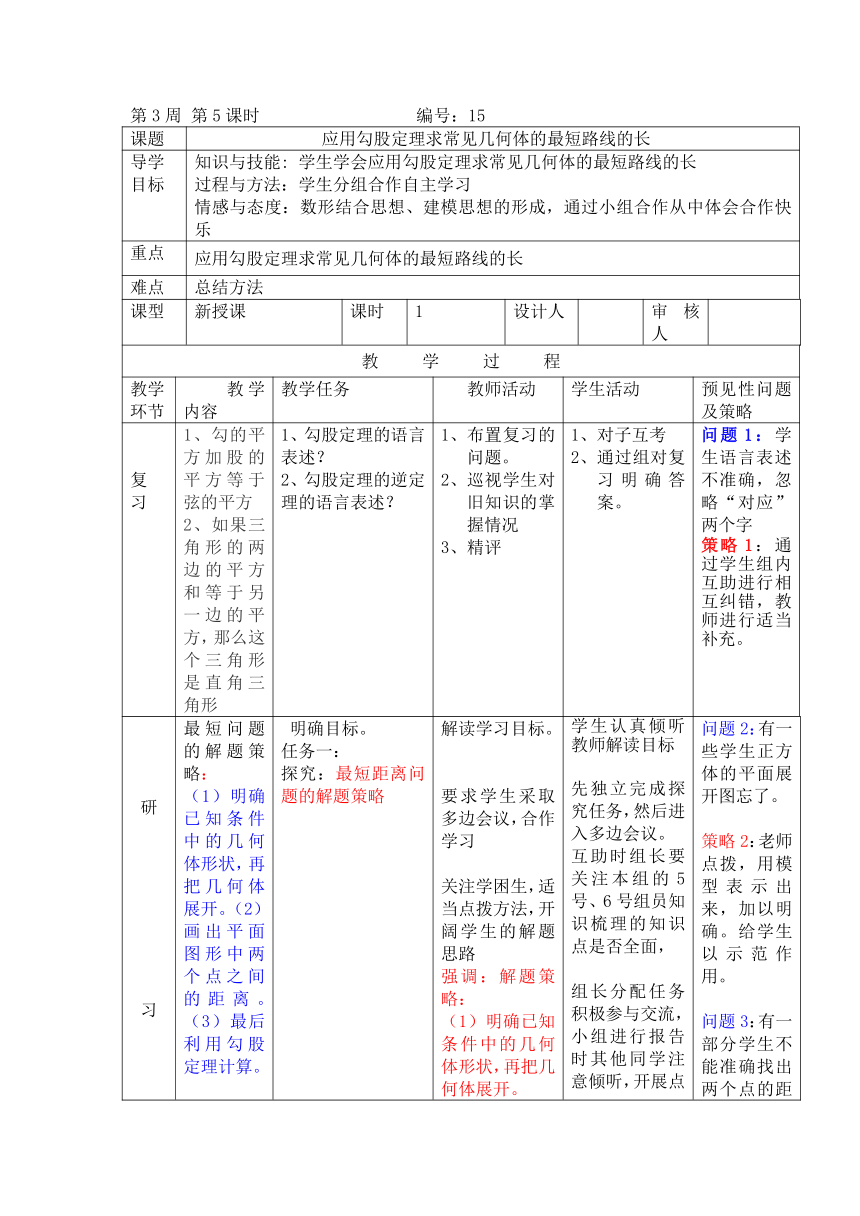
第3周
第5课时
编号:15
课题
应用勾股定理求常见几何体的最短路线的长
导学目标
知识与技能:
学生学会应用勾股定理求常见几何体的最短路线的长过程与方法:学生分组合作自主学习情感与态度:数形结合思想、建模思想的形成,通过小组合作从中体会合作快乐
重点
应用勾股定理求常见几何体的最短路线的长
难点
总结方法
课型
新授课
课时
1
设计人
审核人
教
学
过
程
教学环节
教学内容
教学任务
教师活动
学生活动
预见性问题及策略
复习
1、勾的平方加股的平方等于弦的平方2、如果三角形的两边的平方和等于另一边的平方,那么这个三角形是直角三角形
1、勾股定理的语言表述?2、勾股定理的逆定理的语言表述?
布置复习的问题。巡视学生对旧知识的掌握情况3、精评
对子互考通过组对复习明确答案。
问题1:学生语言表述不准确,忽略“对应”两个字策略1:通过学生组内互助进行相互纠错,教师进行适当补充。
研习
最短问题的解题策略:(1)明确已知条件中的几何体形状,再把几何体展开。(2)画出平面图形中两个点之间的距离。(3)最后利用勾股定理计算。
明确目标。任务一:探究:最短距离问题的解题策略
解读学习目标。要求学生采取多边会议,合作学习关注学困生,适当点拨方法,开阔学生的解题思路强调:解题策略:(1)明确已知条件中的几何体形状,再把几何体展开。(2)画出平面图形中两个点之间的距离。(3)最后利用勾股定理计算。
学生认真倾听教师解读目标先独立完成探究任务,然后进入多边会议。互助时组长要关注本组的5号、6号组员知识梳理的知识点是否全面,组长分配任务积极参与交流,小组进行报告时其他同学注意倾听,开展点评,互相补充,达成共识.在其他小组汇报后积极开展补充、纠错、质疑,归纳点评时注意关注站姿,声音是否洪亮;2、答案是否准确、完整;3、讲解的题目是否能说出分析的思路、解题方法、运用的数学思想等。
问题2:有一些学生正方体的平面展开图忘了。策略2:老师点拨,用模型表示出来,加以明确。给学生以示范作用。问题3:有一部分学生不能准确找出两个点的距离。策略3:精讲。启发学生把已知的立体图形展开,画出平面图形,然后利用勾股定理计算。问题4:平面图画的不对。策略4:启发学生平面展开图有多种展法,选择有需要的点开始。
精习
最短距离问题的解题策略:(1)明确已知条件中的几何体形状,再把几何体展开。(2)画出平面图形中两个点之间的距离。(3)最后利用勾股定理计算。
一、知识梳理二、知识运用
教师巡视,对3号4号进行点拨。关注学生梳理的是否完整
通过多边会议交流完成情况,在交流过程中注意相互补充,相互纠错。
问题:学生想的不全面,提炼的方法不全面准确不太恰当。策略:教师精讲最短距离问题的解题策略,加以提升。
时习
每个学生找出三种不同立体图形题各两道写在纸上
第5课时
编号:15
课题
应用勾股定理求常见几何体的最短路线的长
导学目标
知识与技能:
学生学会应用勾股定理求常见几何体的最短路线的长过程与方法:学生分组合作自主学习情感与态度:数形结合思想、建模思想的形成,通过小组合作从中体会合作快乐
重点
应用勾股定理求常见几何体的最短路线的长
难点
总结方法
课型
新授课
课时
1
设计人
审核人
教
学
过
程
教学环节
教学内容
教学任务
教师活动
学生活动
预见性问题及策略
复习
1、勾的平方加股的平方等于弦的平方2、如果三角形的两边的平方和等于另一边的平方,那么这个三角形是直角三角形
1、勾股定理的语言表述?2、勾股定理的逆定理的语言表述?
布置复习的问题。巡视学生对旧知识的掌握情况3、精评
对子互考通过组对复习明确答案。
问题1:学生语言表述不准确,忽略“对应”两个字策略1:通过学生组内互助进行相互纠错,教师进行适当补充。
研习
最短问题的解题策略:(1)明确已知条件中的几何体形状,再把几何体展开。(2)画出平面图形中两个点之间的距离。(3)最后利用勾股定理计算。
明确目标。任务一:探究:最短距离问题的解题策略
解读学习目标。要求学生采取多边会议,合作学习关注学困生,适当点拨方法,开阔学生的解题思路强调:解题策略:(1)明确已知条件中的几何体形状,再把几何体展开。(2)画出平面图形中两个点之间的距离。(3)最后利用勾股定理计算。
学生认真倾听教师解读目标先独立完成探究任务,然后进入多边会议。互助时组长要关注本组的5号、6号组员知识梳理的知识点是否全面,组长分配任务积极参与交流,小组进行报告时其他同学注意倾听,开展点评,互相补充,达成共识.在其他小组汇报后积极开展补充、纠错、质疑,归纳点评时注意关注站姿,声音是否洪亮;2、答案是否准确、完整;3、讲解的题目是否能说出分析的思路、解题方法、运用的数学思想等。
问题2:有一些学生正方体的平面展开图忘了。策略2:老师点拨,用模型表示出来,加以明确。给学生以示范作用。问题3:有一部分学生不能准确找出两个点的距离。策略3:精讲。启发学生把已知的立体图形展开,画出平面图形,然后利用勾股定理计算。问题4:平面图画的不对。策略4:启发学生平面展开图有多种展法,选择有需要的点开始。
精习
最短距离问题的解题策略:(1)明确已知条件中的几何体形状,再把几何体展开。(2)画出平面图形中两个点之间的距离。(3)最后利用勾股定理计算。
一、知识梳理二、知识运用
教师巡视,对3号4号进行点拨。关注学生梳理的是否完整
通过多边会议交流完成情况,在交流过程中注意相互补充,相互纠错。
问题:学生想的不全面,提炼的方法不全面准确不太恰当。策略:教师精讲最短距离问题的解题策略,加以提升。
时习
每个学生找出三种不同立体图形题各两道写在纸上
