2020-2021学年八年级数学人教版下册《18.1平行四边形》常考题型专题提升训练(word版附答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册《18.1平行四边形》常考题型专题提升训练(word版附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 247.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 20:51:30 | ||
图片预览



文档简介
2020-2021年度人教版八年级数学下册《18.1平行四边形》常考题型专题提升训练(附答案)
1.如图,?ABCD的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( )
A.1.5
B.2
C.2.5
D.3
2.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,则图中面积相等的平行四边形有( )
A.3对
B.2对
C.1对
D.0对
3.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠B,∠C=∠D
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.AB∥CD,AD=BC
4.如图,将?ABCD的一边BC延长至点E,若∠A=110°,则∠1等于( )
A.110°
B.35°
C.70°
D.55°
5.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )
A.2
B.3
C.4
D.5
6.如图,在△ABC中,AB=AC,D、E、F分别是边AB、AC、BC的中点,若CE=2,则四边形ADFE的周长为( )
A.2
B.4
C.6
D.8
7.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC.其中成立的个数是( )
A.1个
B.2个
C.3个
D.4个
8.在?ABCD中,O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长为22cm,则△CDE的周长为( )
A.8cm
B.10cm
C.11cm
D.12cm
9.如图,若平行四边形ABCD的周长为40cm,BC=AB,则BC=( )
A.16cm
B.14cm
C.12cm
D.8cm
10.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=10,BC=15,MN=3,则AC的长是( )
A.12
B.14
C.16
D.18
11.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是
.
12.如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=
s时,以A、C、E、F为顶点四边形是平行四边形.
13.如图,在?ABCD中,BC=9,AB=5,BE平分∠ABC交AD于点E,则DE的长为
.
14.如图,在?ABCD中,AE⊥BC于点E,AF⊥DC于点F,BC=5,AB=4,AE=3,则AF的长度为
.
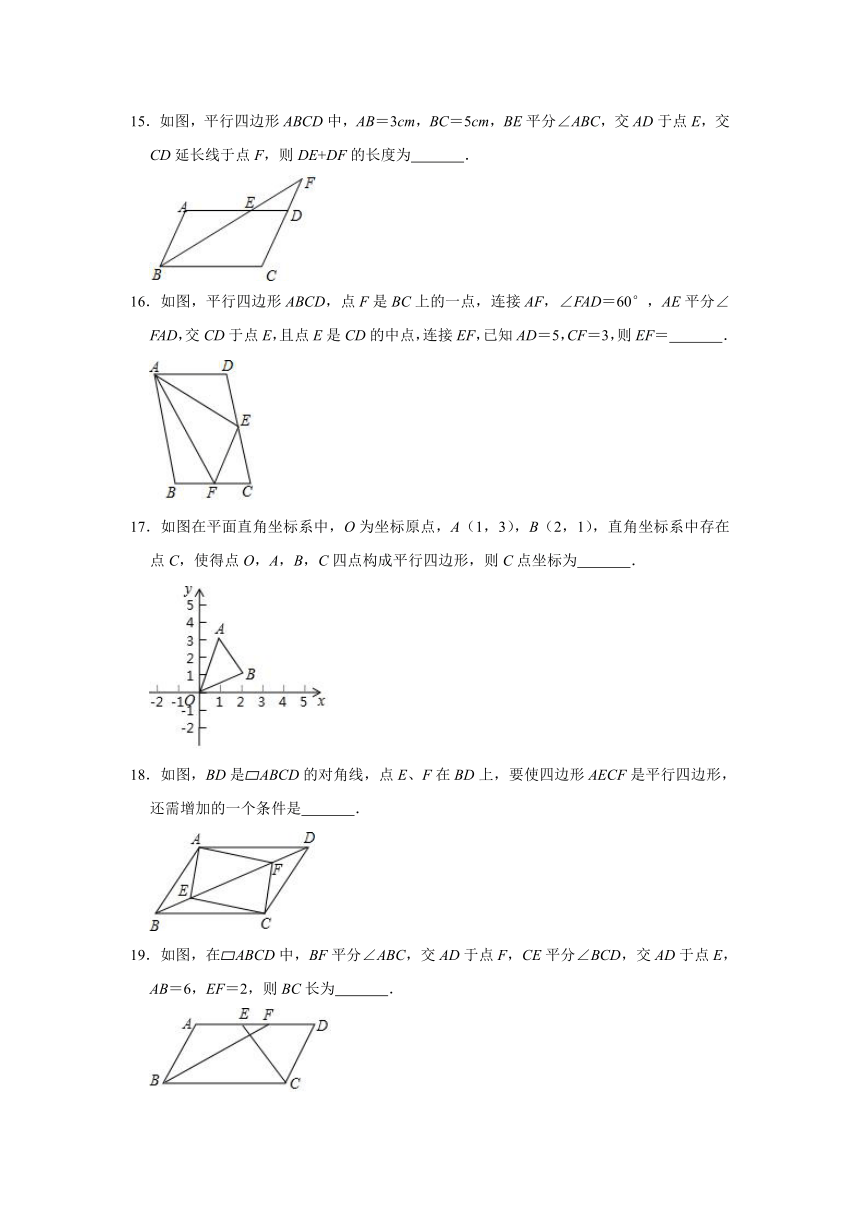
15.如图,平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为
.
16.如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF=
.
17.如图在平面直角坐标系中,O为坐标原点,A(1,3),B(2,1),直角坐标系中存在点C,使得点O,A,B,C四点构成平行四边形,则C点坐标为
.
18.如图,BD是?ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是
.
19.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为
.
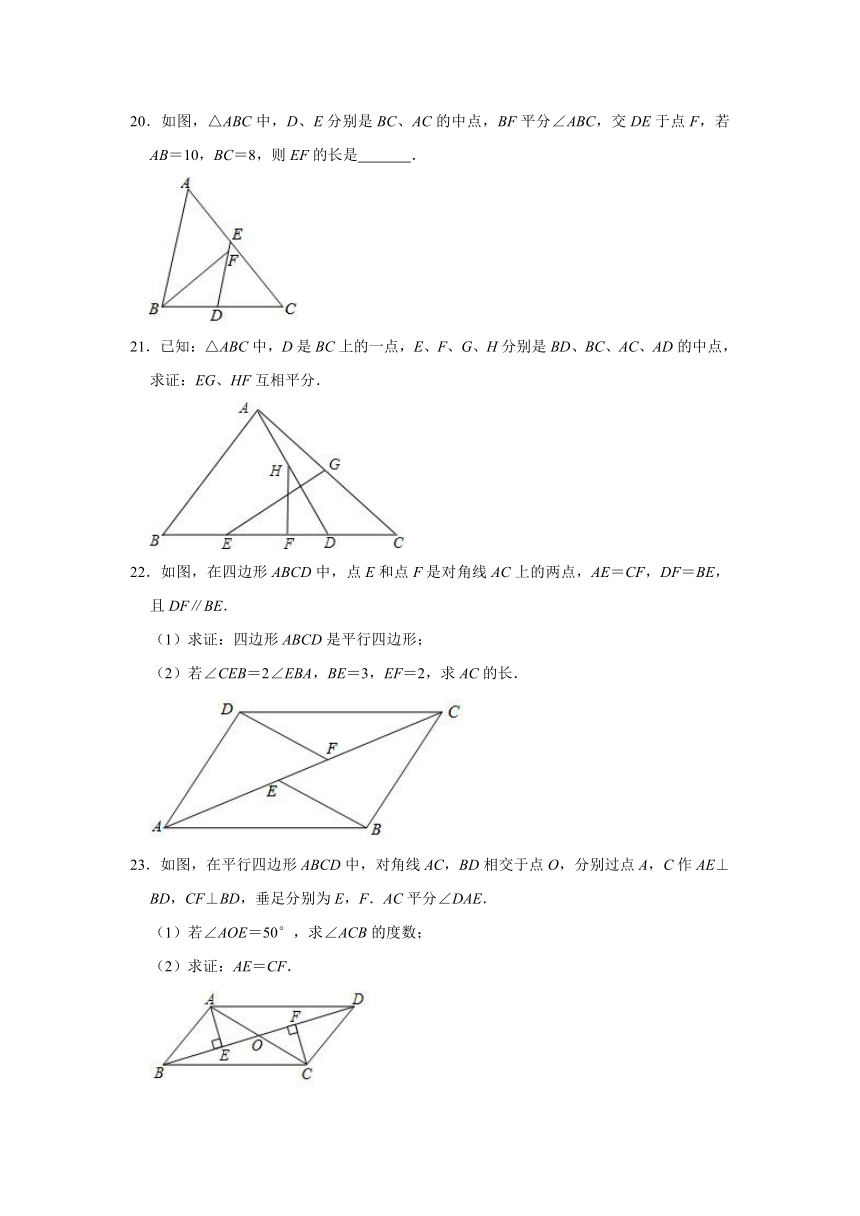
20.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是
.
21.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
22.如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AE=CF,DF=BE,且DF∥BE.
(1)求证:四边形ABCD是平行四边形;
(2)若∠CEB=2∠EBA,BE=3,EF=2,求AC的长.
23.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F.AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF.
24.如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若点F为DC的中点,DG⊥AE于G,且DG=1,AB=4,求AE的长.
25.在平行四边形ABCD中,E是BC边上一点,F是DE上一点,若∠B=∠AFE,AB=AF.求证:
(1)△ADF≌△DEC.
(2)BE=EF.
26.如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在AB上,且BF=DE.
(1)求证:四边形BDEF是平行四边形;
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论.
27.已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
参考答案
1.解:∵四边形ABCD是平行四边形,BD=10,AC=6,
∴OA=3,OB=5,AB∥DC,
∵∠OCD=90°,
∴∠BAO=90°,
∴AB=,
∵E是BC边的中点,OA=OC,
∴2OE=AB,
∴OE=2,
故选:B.
2.解:∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD.
∵BP是平行四边形BEPH的对角线,
∴S△BEP=S△BHP,
∵PD是平行四边形GPFD的对角线,
∴S△GPD=S△FPD.
∴S△ABD﹣S△BEP﹣S△GPD=S△BCD﹣S△BHP﹣S△PFD,即S?AEPG=S?HCFP,
∴S?ABHG=S?BCFE,
同理S?AEFD=S?HCDG.
即:S?ABHG=S?BCFE,S?AGPE=S?HCFP,S?AEFD=S?HCDG.
故选:A.
3.解:
A、∵∠A=∠B,∠C=∠D,∠A+∠B+∠C+∠D=360°,
∴2∠B+2∠C=360°,
∴∠B+∠C=180°,
∴AB∥CD,但不能推出其它条件,即不能推出四边形ABCD是平行四边形,故本选项错误;
B、根据AB=AD,CB=CD不能推出四边形ABCD是平行四边形,故本选项错误;
C、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,故本选项正确;
D、由AB∥CD,AD=BC也可以推出四边形ABCD是等腰梯形,故本选项错误;
故选:C.
4.解:∵平行四边形ABCD的∠A=110°,
∴∠BCD=∠A=110°,
∴∠1=180°﹣∠BCD=180°﹣110°=70°.
故选:C.
5.解:∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∵BC=14,
∴DE=BC=7,
∵∠AFB=90°,AB=8,
∴DF=AB=4,
∴EF=DE﹣DF=7﹣4=3,
故选:B.
6.解:∵点E是AC的中点,AB=AC,
∴AB=AC=4,
∵D是边AB的中点,
∴AD=2,
∵E、F分别是边、AC、BC的中点,
∴DF=AC=2,
同理,EF=2,
∴四边形ADFE的周长=AD+DF+FE+EA=8,
故选:D.
7.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S?ABCD=AB?AC,故②正确,
∵AB=BC,OB=BD,
∵BD>BC,
∴AB≠OB,故③错误;
或∵AC⊥AB,
∴AB<OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
∴OE=AB=BC,故④正确.
故选:C.
8.解:∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,AO=CO,
又∵EO⊥AC,
∴AE=CE,
∵?ABCD的周长为22cm,
∴2(AD+CD)=22cm
∴AD+CD=11cm
∴△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=11cm
故选:C.
9.解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵?ABCD的周长为40cm,
∴AB+BC=20cm,
∵BC=AB,
∴BC=20×=8cm,
故选:D.
10.解:延长线段BN交AC于E.
∵AN平分∠BAC,
∴∠BAN=∠EAN,
在△ABN与△AEN中,
∵,
∴△ABN≌△AEN(ASA),
∴AE=AB=10,BN=NE,
又∵M是△ABC的边BC的中点,
∴CE=2MN=2×3=6,
∴AC=AE+CE=10+6=16.
故选:C.
11.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
12.解:①当点F在C的左侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BC﹣BF=6﹣2t(cm),
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=6﹣2t,
解得:t=2;
②当点F在C的右侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BF﹣BC=2t﹣6(cm),
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=2t﹣6,
解得:t=6;
综上可得:当t=2或6s时,以A、C、E、F为顶点四边形是平行四边形.
故答案为:2或6.
13.解:∵四边形ABCD为平行四边形,
∴AE∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
∵BC=9,CD=5,
∴DE=AD﹣AE=9﹣5=4.
故答案为:4.
14.解:在?ABCD中,CD=AB=4,
∵AE⊥BC,AF⊥DC,
∴S?ABCD=BC?AE=CD?AF,
即5×3=4?AF,
解得AF=.
故答案为:.
15.解:∵平行四边形ABCD,
∴AD∥BC,
∴∠AEB=∠CBF,
∵BE平分∠ABC,
∴∠ABF=∠CBF,
∴∠AEB=∠ABF,
∴AB=AE,
同理可得:BC=CF,
∵AB=3cm,BC=5cm,
∴AE=3cm.CF=5cm,
∴DE=5﹣3=2cm,DF=5﹣3=2cm,
∴DE+DF=2+2=4cm,
故答案为:4cm.
16.解:如图,延长AE,BC交于点G,
∵点E是CD的中点,
∴DE=CE,
∵平行四边形ABCD中,AD∥BC,
∴∠D=∠ECG,
又∵∠AED=∠GEC,
∴△ADE≌△GCE,
∴CG=AD=5,AE=GE,
又∵AE平分∠FAD,AD∥BC,
∴∠FAE=∠DAE=∠G=∠DAF=30°,
∴AF=GF=3+5=8,
又∵E是AG的中点,
∴FE⊥AG,
∴Rt△AEF中,EF=AF=4,
故答案为:4.
17.解:如图所示:
∵以O、A、B、C为顶点的四边形是平行四边形,O(0,0),A(1,3),B(2,0),
∴三种情况:
①当AB为对角线时,点C的坐标为(3,4);
②当OB为对角线时,点C的坐标为(1,﹣2);
③当OA为对角线时,点C的坐标为(﹣1,2);
故答案为(3,4)或(1,﹣2)或(﹣1,2).
18.解:如图,连接AC交BD于点O,
∵四边形ABCD为平行四边形,
∴AO=CO,BO=DO,
∴当BE=DF时,可得OE=OF,则四边形AECF为平行四边形,
∴可增加BE=DF,
故答案为:BE=DF(答案不唯一).
19.解:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
∴∠ABF=∠AFB,
∴AF=AB=6,
同理可证:DE=DC=6,
∵EF=AF+DE﹣AD=2,
即6+6﹣AD=2,
解得AD=10,
∴BC=10,
故答案为:10.
20.解:∵D、E分别是BC、AC的中点,
∴DE=AB=5,DE∥AB,BD=BC=4,
∴∠ABF=∠DFB,
∵BF平分∠ABC,
∴∠ABF=∠DBF,
∴∠DBF=∠DFB,
∴DF=DB=4,
∴EF=DE﹣DF=1,
故答案为:1.
21.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
22.(1)证明:∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵DF∥BE,
∴∠DFA=∠BEC,
在△ADF和△CBE中,,
∴△ADF≌△CBE(SAS),
∴AD=CB,∠DAF=∠BCE,
∴AD∥CB,
∴四边形ABCD是平行四边形;
(2)解:∵∠CEB=∠EBA+∠EAB=2∠EBA,
∴∠EAB=∠EBA,
∴AE=BE=3,
∴CF=AE=3,
∴AC=AE+EF+CF=3+2+3=8.
23.(1)解:∵AE⊥BD,
∴∠AEO=90°,
∵∠AOE=50°,
∴∠EAO=40°,
∵CA平分∠DAE,
∴∠DAC=∠EAO=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ACB=∠DAC=40°;
(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS),
∴AE=CF.
24.(1)证明:∵AE为∠BAD的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
∵F为DC的中点,AB=4,
∴DF=CF=DA=2.
∵DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).
∴AF=EF,
∴AE=2AF=4.
25.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,AD=BC,AB∥CD,
∴∠ADF=∠DEC,∠B+∠C=180°,
∵∠AFE+∠AFD=180°,∠B=∠AFE,
∴∠AFD=∠C,
∵AB=AF,
∴AF=DC,
在△ADF和△DEC中,
∴△ADF≌△DEC(AAS);
(2)证明:∵△ADF≌△DEC,
∴AD=DE,DF=EC,
又∵AD=BC,
∴BC=DE,
∴BC﹣EC=DE﹣DF,
即BE=EF.
26.(1)证明:延长CE交AB于点G,
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA).
∴GE=EC.
∵BD=CD,
∴DE为△CGB的中位线,
∴DE∥AB.
∵DE=BF,
∴四边形BDEF是平行四边形.
(2)解:BF=(AB﹣AC).
理由如下:
∵四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DE=BG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF=(AB﹣AG)=(AB﹣AC).
27.证明:(1)四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAM=∠FCN,
又∵AD∥BC,
∴∠E=∠F.
∵在△AEM与△CFN中,
,
∴△AEM≌△CFN(ASA);
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD
又由(1)得AM=CN,
∴BM=DN,BM∥DN,
∴四边形BMDN是平行四边形.
1.如图,?ABCD的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( )
A.1.5
B.2
C.2.5
D.3
2.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,则图中面积相等的平行四边形有( )
A.3对
B.2对
C.1对
D.0对
3.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠B,∠C=∠D
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.AB∥CD,AD=BC
4.如图,将?ABCD的一边BC延长至点E,若∠A=110°,则∠1等于( )
A.110°
B.35°
C.70°
D.55°
5.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )
A.2
B.3
C.4
D.5
6.如图,在△ABC中,AB=AC,D、E、F分别是边AB、AC、BC的中点,若CE=2,则四边形ADFE的周长为( )
A.2
B.4
C.6
D.8
7.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE=BC.其中成立的个数是( )
A.1个
B.2个
C.3个
D.4个
8.在?ABCD中,O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长为22cm,则△CDE的周长为( )
A.8cm
B.10cm
C.11cm
D.12cm
9.如图,若平行四边形ABCD的周长为40cm,BC=AB,则BC=( )
A.16cm
B.14cm
C.12cm
D.8cm
10.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=10,BC=15,MN=3,则AC的长是( )
A.12
B.14
C.16
D.18
11.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是
.
12.如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=
s时,以A、C、E、F为顶点四边形是平行四边形.
13.如图,在?ABCD中,BC=9,AB=5,BE平分∠ABC交AD于点E,则DE的长为
.
14.如图,在?ABCD中,AE⊥BC于点E,AF⊥DC于点F,BC=5,AB=4,AE=3,则AF的长度为
.
15.如图,平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为
.
16.如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF=
.
17.如图在平面直角坐标系中,O为坐标原点,A(1,3),B(2,1),直角坐标系中存在点C,使得点O,A,B,C四点构成平行四边形,则C点坐标为
.
18.如图,BD是?ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是
.
19.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为
.
20.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是
.
21.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
22.如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AE=CF,DF=BE,且DF∥BE.
(1)求证:四边形ABCD是平行四边形;
(2)若∠CEB=2∠EBA,BE=3,EF=2,求AC的长.
23.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F.AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF.
24.如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若点F为DC的中点,DG⊥AE于G,且DG=1,AB=4,求AE的长.
25.在平行四边形ABCD中,E是BC边上一点,F是DE上一点,若∠B=∠AFE,AB=AF.求证:
(1)△ADF≌△DEC.
(2)BE=EF.
26.如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在AB上,且BF=DE.
(1)求证:四边形BDEF是平行四边形;
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论.
27.已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
参考答案
1.解:∵四边形ABCD是平行四边形,BD=10,AC=6,
∴OA=3,OB=5,AB∥DC,
∵∠OCD=90°,
∴∠BAO=90°,
∴AB=,
∵E是BC边的中点,OA=OC,
∴2OE=AB,
∴OE=2,
故选:B.
2.解:∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD.
∵BP是平行四边形BEPH的对角线,
∴S△BEP=S△BHP,
∵PD是平行四边形GPFD的对角线,
∴S△GPD=S△FPD.
∴S△ABD﹣S△BEP﹣S△GPD=S△BCD﹣S△BHP﹣S△PFD,即S?AEPG=S?HCFP,
∴S?ABHG=S?BCFE,
同理S?AEFD=S?HCDG.
即:S?ABHG=S?BCFE,S?AGPE=S?HCFP,S?AEFD=S?HCDG.
故选:A.
3.解:
A、∵∠A=∠B,∠C=∠D,∠A+∠B+∠C+∠D=360°,
∴2∠B+2∠C=360°,
∴∠B+∠C=180°,
∴AB∥CD,但不能推出其它条件,即不能推出四边形ABCD是平行四边形,故本选项错误;
B、根据AB=AD,CB=CD不能推出四边形ABCD是平行四边形,故本选项错误;
C、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,故本选项正确;
D、由AB∥CD,AD=BC也可以推出四边形ABCD是等腰梯形,故本选项错误;
故选:C.
4.解:∵平行四边形ABCD的∠A=110°,
∴∠BCD=∠A=110°,
∴∠1=180°﹣∠BCD=180°﹣110°=70°.
故选:C.
5.解:∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∵BC=14,
∴DE=BC=7,
∵∠AFB=90°,AB=8,
∴DF=AB=4,
∴EF=DE﹣DF=7﹣4=3,
故选:B.
6.解:∵点E是AC的中点,AB=AC,
∴AB=AC=4,
∵D是边AB的中点,
∴AD=2,
∵E、F分别是边、AC、BC的中点,
∴DF=AC=2,
同理,EF=2,
∴四边形ADFE的周长=AD+DF+FE+EA=8,
故选:D.
7.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S?ABCD=AB?AC,故②正确,
∵AB=BC,OB=BD,
∵BD>BC,
∴AB≠OB,故③错误;
或∵AC⊥AB,
∴AB<OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
∴OE=AB=BC,故④正确.
故选:C.
8.解:∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,AO=CO,
又∵EO⊥AC,
∴AE=CE,
∵?ABCD的周长为22cm,
∴2(AD+CD)=22cm
∴AD+CD=11cm
∴△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=11cm
故选:C.
9.解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵?ABCD的周长为40cm,
∴AB+BC=20cm,
∵BC=AB,
∴BC=20×=8cm,
故选:D.
10.解:延长线段BN交AC于E.
∵AN平分∠BAC,
∴∠BAN=∠EAN,
在△ABN与△AEN中,
∵,
∴△ABN≌△AEN(ASA),
∴AE=AB=10,BN=NE,
又∵M是△ABC的边BC的中点,
∴CE=2MN=2×3=6,
∴AC=AE+CE=10+6=16.
故选:C.
11.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
12.解:①当点F在C的左侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BC﹣BF=6﹣2t(cm),
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=6﹣2t,
解得:t=2;
②当点F在C的右侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BF﹣BC=2t﹣6(cm),
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=2t﹣6,
解得:t=6;
综上可得:当t=2或6s时,以A、C、E、F为顶点四边形是平行四边形.
故答案为:2或6.
13.解:∵四边形ABCD为平行四边形,
∴AE∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
∵BC=9,CD=5,
∴DE=AD﹣AE=9﹣5=4.
故答案为:4.
14.解:在?ABCD中,CD=AB=4,
∵AE⊥BC,AF⊥DC,
∴S?ABCD=BC?AE=CD?AF,
即5×3=4?AF,
解得AF=.
故答案为:.
15.解:∵平行四边形ABCD,
∴AD∥BC,
∴∠AEB=∠CBF,
∵BE平分∠ABC,
∴∠ABF=∠CBF,
∴∠AEB=∠ABF,
∴AB=AE,
同理可得:BC=CF,
∵AB=3cm,BC=5cm,
∴AE=3cm.CF=5cm,
∴DE=5﹣3=2cm,DF=5﹣3=2cm,
∴DE+DF=2+2=4cm,
故答案为:4cm.
16.解:如图,延长AE,BC交于点G,
∵点E是CD的中点,
∴DE=CE,
∵平行四边形ABCD中,AD∥BC,
∴∠D=∠ECG,
又∵∠AED=∠GEC,
∴△ADE≌△GCE,
∴CG=AD=5,AE=GE,
又∵AE平分∠FAD,AD∥BC,
∴∠FAE=∠DAE=∠G=∠DAF=30°,
∴AF=GF=3+5=8,
又∵E是AG的中点,
∴FE⊥AG,
∴Rt△AEF中,EF=AF=4,
故答案为:4.
17.解:如图所示:
∵以O、A、B、C为顶点的四边形是平行四边形,O(0,0),A(1,3),B(2,0),
∴三种情况:
①当AB为对角线时,点C的坐标为(3,4);
②当OB为对角线时,点C的坐标为(1,﹣2);
③当OA为对角线时,点C的坐标为(﹣1,2);
故答案为(3,4)或(1,﹣2)或(﹣1,2).
18.解:如图,连接AC交BD于点O,
∵四边形ABCD为平行四边形,
∴AO=CO,BO=DO,
∴当BE=DF时,可得OE=OF,则四边形AECF为平行四边形,
∴可增加BE=DF,
故答案为:BE=DF(答案不唯一).
19.解:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
∴∠ABF=∠AFB,
∴AF=AB=6,
同理可证:DE=DC=6,
∵EF=AF+DE﹣AD=2,
即6+6﹣AD=2,
解得AD=10,
∴BC=10,
故答案为:10.
20.解:∵D、E分别是BC、AC的中点,
∴DE=AB=5,DE∥AB,BD=BC=4,
∴∠ABF=∠DFB,
∵BF平分∠ABC,
∴∠ABF=∠DBF,
∴∠DBF=∠DFB,
∴DF=DB=4,
∴EF=DE﹣DF=1,
故答案为:1.
21.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
22.(1)证明:∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵DF∥BE,
∴∠DFA=∠BEC,
在△ADF和△CBE中,,
∴△ADF≌△CBE(SAS),
∴AD=CB,∠DAF=∠BCE,
∴AD∥CB,
∴四边形ABCD是平行四边形;
(2)解:∵∠CEB=∠EBA+∠EAB=2∠EBA,
∴∠EAB=∠EBA,
∴AE=BE=3,
∴CF=AE=3,
∴AC=AE+EF+CF=3+2+3=8.
23.(1)解:∵AE⊥BD,
∴∠AEO=90°,
∵∠AOE=50°,
∴∠EAO=40°,
∵CA平分∠DAE,
∴∠DAC=∠EAO=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ACB=∠DAC=40°;
(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS),
∴AE=CF.
24.(1)证明:∵AE为∠BAD的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB.
∴∠DAE=∠E.
∴∠BAE=∠E.
∴AB=BE.
∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠BAF=∠DFA.
∴∠DAF=∠DFA.
∴DA=DF.
∵F为DC的中点,AB=4,
∴DF=CF=DA=2.
∵DG⊥AE,DG=1,
∴AG=GF.
∴AG=.
∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).
∴AF=EF,
∴AE=2AF=4.
25.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,AD=BC,AB∥CD,
∴∠ADF=∠DEC,∠B+∠C=180°,
∵∠AFE+∠AFD=180°,∠B=∠AFE,
∴∠AFD=∠C,
∵AB=AF,
∴AF=DC,
在△ADF和△DEC中,
∴△ADF≌△DEC(AAS);
(2)证明:∵△ADF≌△DEC,
∴AD=DE,DF=EC,
又∵AD=BC,
∴BC=DE,
∴BC﹣EC=DE﹣DF,
即BE=EF.
26.(1)证明:延长CE交AB于点G,
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA).
∴GE=EC.
∵BD=CD,
∴DE为△CGB的中位线,
∴DE∥AB.
∵DE=BF,
∴四边形BDEF是平行四边形.
(2)解:BF=(AB﹣AC).
理由如下:
∵四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DE=BG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF=(AB﹣AG)=(AB﹣AC).
27.证明:(1)四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAM=∠FCN,
又∵AD∥BC,
∴∠E=∠F.
∵在△AEM与△CFN中,
,
∴△AEM≌△CFN(ASA);
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD
又由(1)得AM=CN,
∴BM=DN,BM∥DN,
∴四边形BMDN是平行四边形.
