2020-2021学年八年级数学人教版下册《18.2特殊的平行四边形》经典好题专题提升训练(word版附答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册《18.2特殊的平行四边形》经典好题专题提升训练(word版附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 367.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览


文档简介
2021年人教版八年级数学下册《18.2特殊的平行四边形》经典好题专题提升训练(附答案)
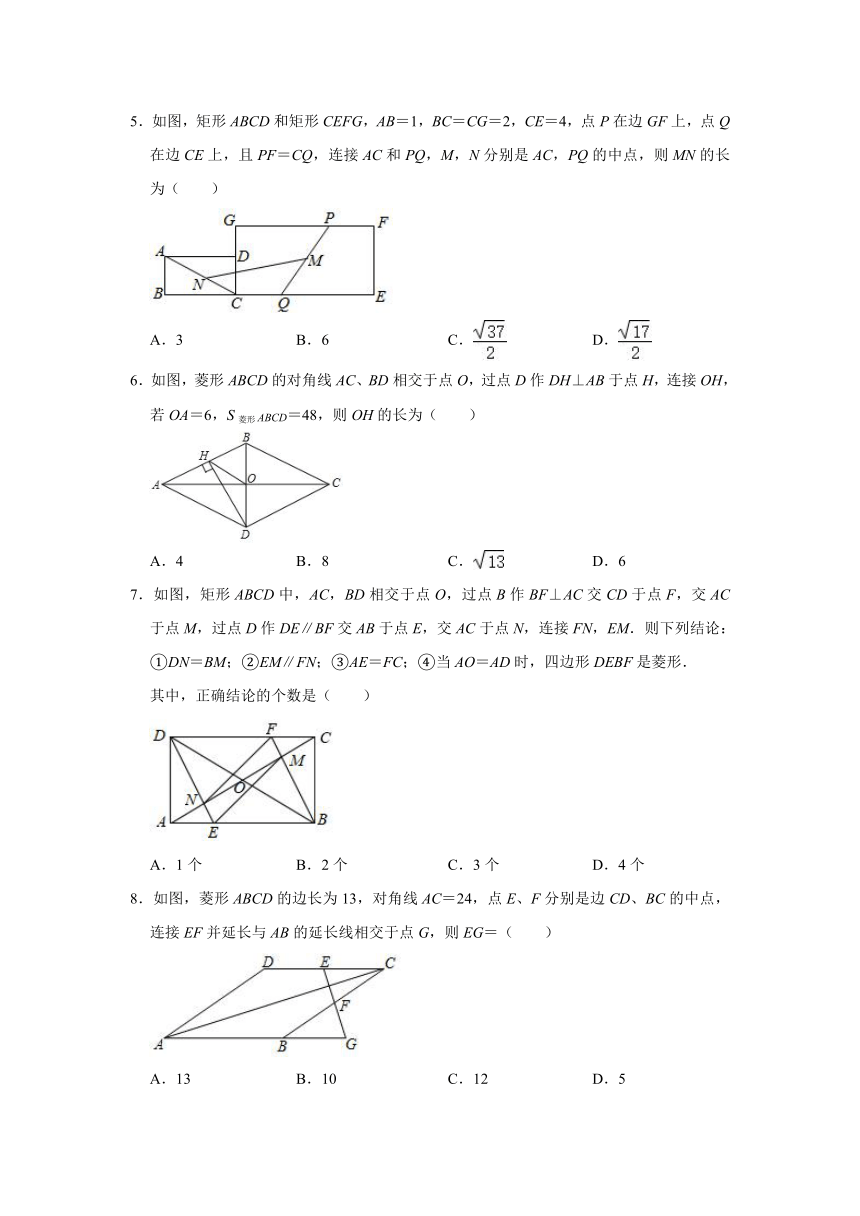
1.如图,在平行四边形ABCD中,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE,添加一个条件,使四边形AEBD是菱形,这个条件是( )
A.∠BAD=∠BDA
B.AB=DE
C.DF=EF
D.∠BDC=∠BAD
2.如图,已知大矩形ABCD由①②③④四个小矩形组成,其中AE=CG,则只需要知道其中一个小矩形的面积就可以求出图中阴影部分的面积,这个小矩形是( )
A.①
B.②
C.③
D.④
3.如图,在矩形ABCD中,点A的坐标是(1,0),点C的坐标是(﹣2,4),则BD的长是( )
A.
B.5
C.3
D.4
4.在平面直角坐标系中,菱形ABCD的顶点的坐标A、B、C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为( )
A.(0,﹣1)
B.(﹣2,1)
C.(2,1)
D.(0,﹣2)
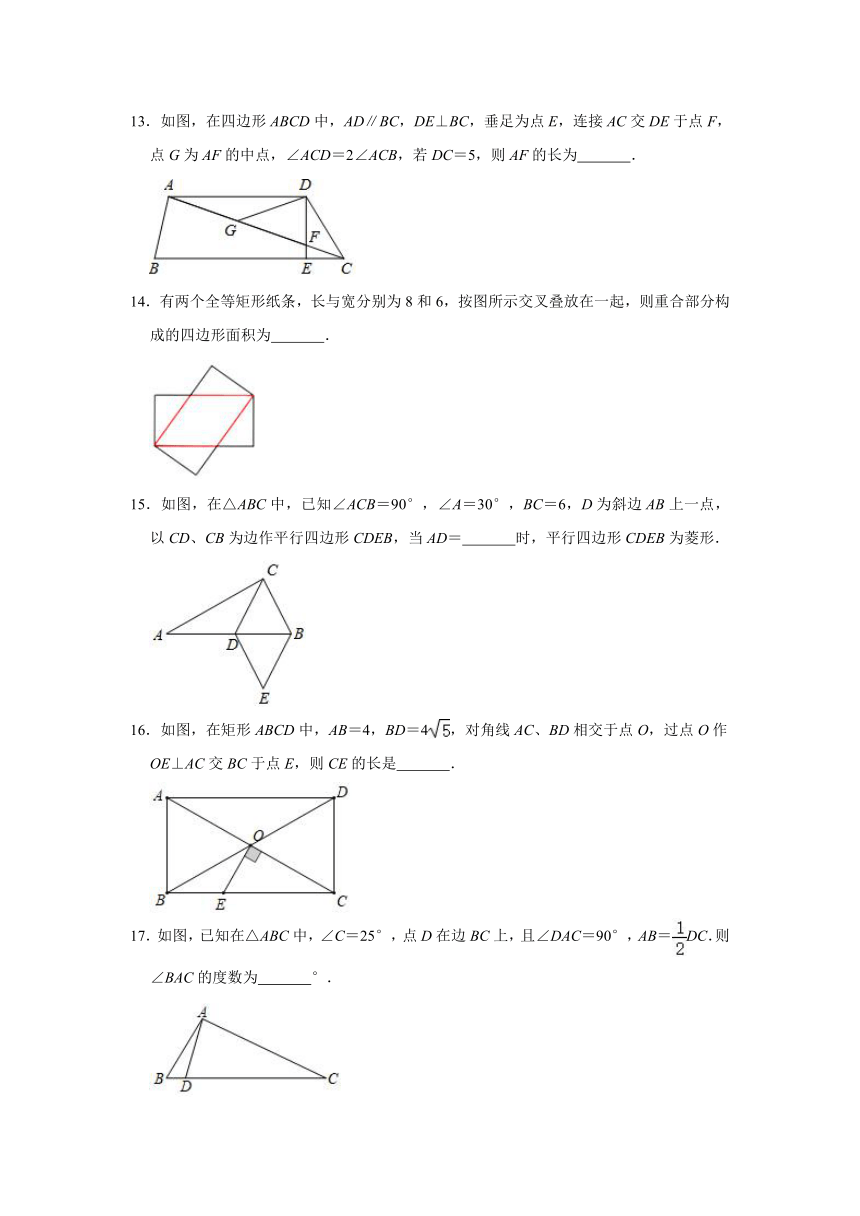
5.如图,矩形ABCD和矩形CEFG,AB=1,BC=CG=2,CE=4,点P在边GF上,点Q在边CE上,且PF=CQ,连接AC和PQ,M,N分别是AC,PQ的中点,则MN的长为( )
A.3
B.6
C.
D.
6.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为( )
A.4
B.8
C.
D.6
7.如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:
①DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.
其中,正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
8.如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )
A.13
B.10
C.12
D.5
9.如图,正方形ABCD中,AB=,点E是对角线AC上一点,EF⊥AB于点F,连接DE,当∠ADE=22.5°时,EF的长是( )
A.1
B.2﹣2
C.﹣1
D.
10.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4
B.2
C.
D.2
11.如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为( )
A.15°
B.22.5°
C.25°
D.17.5°
12.如图,已知菱形ABCD的顶点A(﹣,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→……的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标是
.
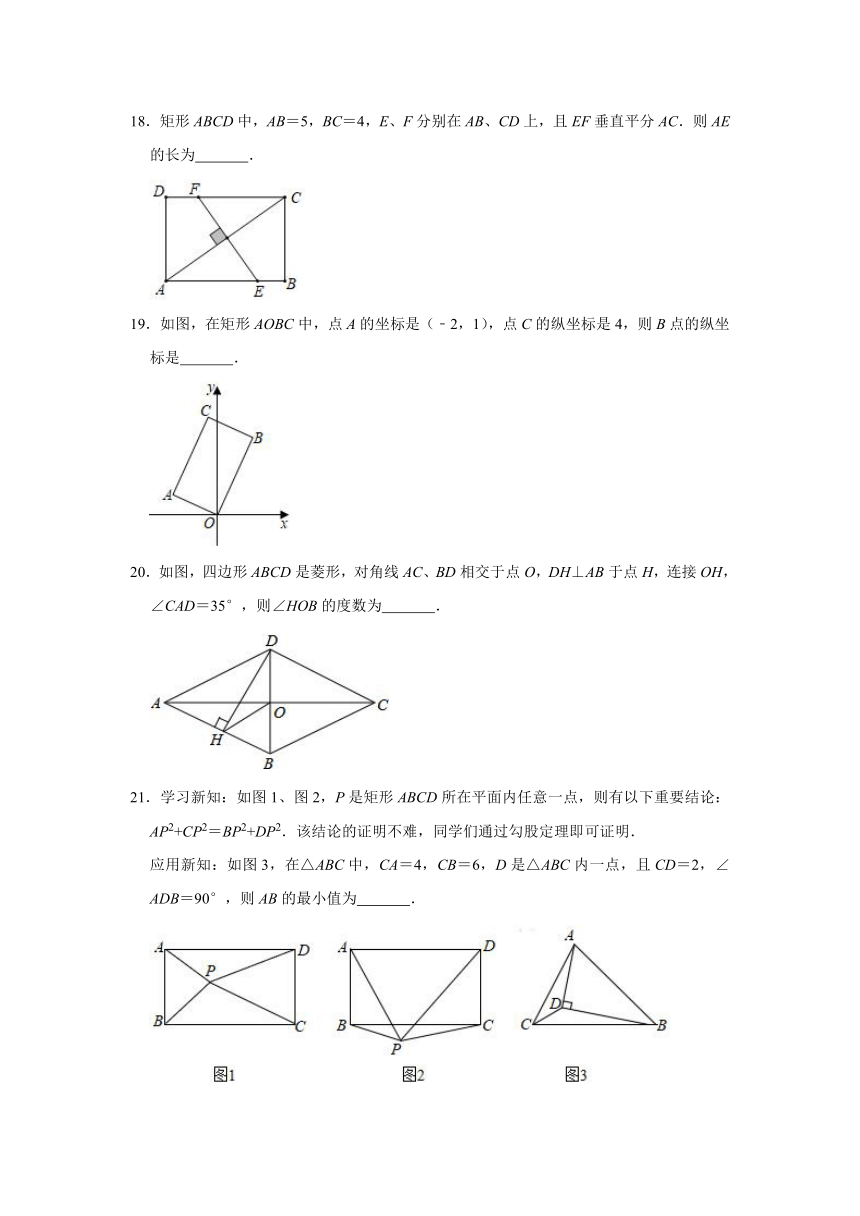
13.如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB,若DC=5,则AF的长为
.
14.有两个全等矩形纸条,长与宽分别为8和6,按图所示交叉叠放在一起,则重合部分构成的四边形面积为
.
15.如图,在△ABC中,已知∠ACB=90°,∠A=30°,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=
时,平行四边形CDEB为菱形.
16.如图,在矩形ABCD中,AB=4,BD=4,对角线AC、BD相交于点O,过点O作OE⊥AC交BC于点E,则CE的长是
.
17.如图,已知在△ABC中,∠C=25°,点D在边BC上,且∠DAC=90°,AB=DC.则∠BAC的度数为
°.
18.矩形ABCD中,AB=5,BC=4,E、F分别在AB、CD上,且EF垂直平分AC.则AE的长为
.
19.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B点的纵坐标是
.
20.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=35°,则∠HOB的度数为
.
21.学习新知:如图1、图2,P是矩形ABCD所在平面内任意一点,则有以下重要结论:AP2+CP2=BP2+DP2.该结论的证明不难,同学们通过勾股定理即可证明.
应用新知:如图3,在△ABC中,CA=4,CB=6,D是△ABC内一点,且CD=2,∠ADB=90°,则AB的最小值为
.
22.如图,在平面直角坐标中,D是正方形ABCO的边AB上一点,以OD为边的等边△ODE,点E在x轴正半轴上,若点B的坐标为(3,3),则点E的坐标为
.
23.如图,在正方形ABCD中,BE平分∠CBD,EF⊥BD于点F.若DE=,则BC的长为
.
24.如图所示,平行四边形ABCD,对角线BD平分∠ABC;
(1)求证:四边形ABCD为菱形;
(2)已知AE⊥BC于E,若CE=2BE=4,求BD.
25.如图,已知?ABCD的对角线AC、BD交于点O,且∠1=∠2.
(1)求证:?ABCD是菱形.
(2)F为AD上一点,连接BF交AC于E,且AE=AF,若AF=3,AB=5,求AO的长.
26.如图,已知菱形ABCD的对角线AC、BD相交于点O,分别过A、D两点作AO、DO的垂线,两垂线交于点E.
(1)求证:四边形AODE是矩形;
(2)若四边形AODE的面积为12,AD=5,求四边形AODE的周长.
27.如图,在矩形ABCD中,点O为对角线AC的中点,点E是CD上一点,连接EO并延长交AB于点F,连接AE、CF.
(1)求证:△COE≌△AOF;
(2)当∠DEA=2∠CAB时,试判断四边形AECF的形状,并说明理由.
28.如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
29.正方形ABCD中,M为射线CD上一点(不与D重合),以CM为边,在正方形ABCD的异侧作正方形CFGM,连接BM,DF,直线BM与DF交于点E.
(1)如图1,若M在CD的延长线上,求证:DF=BM,DF⊥BM;
(2)如图2,若M移到边CD上.
①在(1)中结论是否仍成立?(直接回答不需证明)
②连接BD,若BD=BF,且正方形CFGM的边长为1,试求正方形ABCD的周长.
30.如图,在边长为1的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:△PDE≌△QCE;
(2)若PB=PQ,点F是BP的中点,连接EF、AF,
①求证:四边形AFEP是平行四边形;②求PE的长.
31.如图,已知四边形ABCD是正方形,点E、F分别在AD、DC上,BE与AF相交于点G,且BE=AF.
(1)求证:△ABE≌△DAF;
(2)求证:BE⊥AF;
(3)如果正方形ABCD的边长为5,AE=2,点H为BF的中点,连接GH.求GH的长.
参考答案
1.解:添加一个条件∠BDC=∠BAD,使四边形AEBD是菱形;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∠BAD=∠C,
∴AD∥BE,
∴∠ADF=∠BEF,
∵点F是AB的中点,
∴AF=BF,
在△ADF和△BEF中,,
∴△ADF≌△BEF(AAS),
∴AD=BE,
又∵AD∥BE,
∴四边形AEBD是平行四边形,
∵∠BDC=∠BAD,∠BAD=∠C,
∴∠BDC=∠C,
∴BD=BC,
∵AD=BC,AD=BE,
∴BD=BE,
∴四边形AEBD是菱形;
故选:D.
2.解:如图所示:
∵四边形ABCD和四边形③是矩形,
∴AB=CD,FP=CG,
∵AE=CG,
∴BE=DG,
∴阴影部分的面积=△BFD的面积﹣△BFP的面积=BF×CD﹣BF×FP=BF×(CD﹣CG)=BF×DG=BF×BE=矩形②面积,
故选:B.
3.解:连接AC,如图:
∵四边形ABCD是矩形,
∴BD=AC,
∵点A的坐标是(1,0),点C的坐标是(﹣2,4),
∴AC==5,
∴BD=AC=5,
故选:B.
4.解:如图所示,
∵菱形ABCD的对角线互相垂直平分,A、B、C分别为(﹣2,0),(0,1),(2,0),
∴D(0,﹣1).
故选:A.
5.解:连接CF,交PQ于R,延长AD交EF于H,连接AF,如图所示:
则四边形ABEH是矩形,
∴HE=AB=1,AH=BE=BC+CE=2+4=6,
∵四边形CEFG是矩形,
∴FG∥CE,EF=CG=2,
∴∠RFP=∠RCQ,∠RPF=∠RQC,FH=EF﹣HE=2﹣1=1,
在Rt△AHF中,由勾股定理得:AF===,
在△RFP和△RCQ中,,
∴△RFP≌△RCQ(ASA),
∴RP=RQ,
∴点R与点M重合,
∵点N是AC的中点,
∴MN是△CAF的中位线,
∴MN=AF=×=,
故选:C.
6.解:∵四边形ABCD是菱形,
∴OA=OC=6,OB=OD,AC⊥BD,
∴AC=12,
∵DH⊥AB,
∴∠BHD=90°,
∴OH=BD,
∵菱形ABCD的面积=×AC×BD=×12×BD=48,
∴BD=8,
∴OH=BD=4;
故选:A.
7.解:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∠DAE=∠BCF=90°,OD=OB=OA=OC,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∵BF⊥AC,DE∥BF,
∴DE⊥AC,
∴∠DNA=∠BMC=90°,
在△DNA和△BMC中,,
∴△DNA≌△BMC(AAS),
∴DN=BM,∠ADE=∠CBF,故①正确;
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA),
∴AE=FC,DE=BF,故③正确;
∴DE﹣DN=BF﹣BM,即NE=MF,
∵DE∥BF,
∴四边形NEMF是平行四边形,
∴EM∥FN,故②正确;
∵AB=CD,AE=CF,
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵AO=AD,
∴AO=AD=OD,
∴△AOD是等边三角形,
∴∠ADO=∠DAN=60°,
∴∠ABD=90°﹣∠ADO=30°,
∵DE⊥AC,
∴∠ADN=ODN=30°,
∴∠ODN=∠ABD,
∴DE=BE,
∴四边形DEBF是菱形;故④正确;
正确结论的个数是4个,
故选:D.
8.解:连接BD,交AC于点O,如图:
∵菱形ABCD的边长为13,点E、F分别是边CD、BC的中点,
∴AB∥CD,AB=BC=CD=DA=13,EF∥BD,
∵AC、BD是菱形的对角线,AC=24,
∴AC⊥BD,AO=CO=12,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∴四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,∵OC⊥OD,CD=13,CO=12,
∴OB=OD==5,
∴BD=2OD=10,
∴EG=BD=10;
故选:B.
9.解:∵四边形ABCD是正方形,
∴AB=CD=BC=,∠B=∠ADC=90°,∠BAC=∠CAD=45°,
∴AC=AB=2,
∵∠ADE=22.5°,
∴∠CDE=90°﹣22.5°=67.5°,
∵∠CED=∠CAD+∠ADE=45°+22.5°=67.5°,
∴∠CDE=∠CED,
∴CD=CE=,
∴AE=2﹣,
∵EF⊥AB,
∴∠AFE=90°,
∴△AFE是等腰直角三角形,
∴EF==﹣1,
故选:C.
10.解:在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,
∴OA=AC==.
故选:C.
11.解:∵四边形ABCD是正方形,
∴∠BOC=90°,∠OBC=45°,
∵BP=OB,
∴∠BOP=∠BPO=(180°﹣45°)=67.5°,
∴∠COP=90°﹣67.5°=22.5°.
故选:B.
12.解:∵在菱形ABCD中,∠DAB=60°,
∴∠OAD=30°,
∵A(﹣,0)
∴在Rt△AOD中,OA=,
∴OD=OA?tan30°=1,
∴AD=2,
∵动点P绕菱形一周的时间为2×4÷0.5=16(秒),
又2020÷16=126…4,
∴第2020秒时,点P运动到点B处,
∵OB=OD=1,
∴此时点P的坐标为(0,﹣1).
故答案为:(0,﹣1).
13.解:∵AD∥BC,DE⊥BC,
∴AD⊥DE,∠GAD=∠ACB,
∴∠ADF=90°,
∵点G为AF的中点,
∴DG=AF=GA,
∴∠GAD=∠GDA,
∴∠DGC=∠GAD+∠GDA=2∠GAD,
∵AD∥BC,
∴∠GAD=∠ACB,
∵∠ACD=2∠ACB,
∴∠DGC=∠ACD,
∴DG=DC=5,
∴AF=10,
故答案为:10.
14.解:如图所示:
由题意得:矩形ABCD≌矩形BEDF,
∴∠A=90°,AB=BE=6,AD∥BC,BF∥DE,AD=8,
∴四边形BGDH是平行四边形,
∴平行四边形BGDH的面积=BG×AB=BH×BE,
∴BG=BH,
∴四边形BGDH是菱形,
∴BH=DH,
设BH=DH=x,则AH=8﹣x,
在Rt△ABH中,由勾股定理得:62+(8﹣x)2=x2,
解得:x=,
∴BG=,
∴四边形BGDH的面积=BG×AB=×6=;
故答案为:.
15.解:连接CE交AB于点O,如图所示:
∵Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,
∴AB=2BC=12,AC===6,
若平行四边形CDEB为菱形时,CE⊥BD,OD=OB,CD=CB,
∵AB?OC=AC?BC,
∴OC===3,
∴OB===3,
∴AD=AB﹣2OB=12﹣2×3=6,
故答案为:6.
16.解:如图,连接AE,
∵在矩形ABCD中,OA=OC,OE⊥AC,
∴OE垂直平分AC,
∴AE=CE,
∵∠BAD=90°,AB=4,BD=4,
∴AD=BC==8,
∴BE=BC﹣CE=8﹣CE,
∴在Rt△ABE中,根据勾股定理,得
AE2=AB2+BE2,
即CE2=42+(8﹣CE)2,
解得CE=5.
故答案为:5.
17.解:取CD的中点E,连接AE,
在Rt△ADC中,DE=EC,
∴AE=CD=ED=EC,
∴∠EAC=∠C=25°,
∴∠AED=∠EAC+∠C=50°,
∵AE=ED,
∴∠EAD=∠EDA=65°,
∵AB=DC,AE=CD,
∴AB=AE,
∴∠BAE=80°,
∴∠BAC=∠BAE+∠EAC=105°,
故答案为:105.
18.解:如图,连接CE,
∵EF垂直平分AC,
∴CE=AE,
则BE=AB﹣AE=5﹣AE,
∵矩形ABCD中,∠B=90°,
在Rt△CBE中,根据勾股定理,得
CE2=BE2+BC2,
即:AE2=(5﹣AE)2+42,
解得AE=4.1.
答:AE的长为4.1.
故答案为:4.1.
19.解:如图,
过点A作AD⊥x轴于点D,
过点B作BE⊥x轴于点E,
过点C作CF∥y轴,过点A作AF∥x轴,交点为F,
则AF⊥CF,
延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴OB=AC,AC∥OB,
∴∠CAF=∠CHO=∠BOE,
∵∠AFC=∠OEB=90°,
∴△AFC≌△OEB(AAS),
∴CF=BE=4﹣1=3,
故答案为:3.
20.解:∵四边形ABCD是菱形,
∴BO=DO,
∵DH⊥AB,
∴∠DHB=90°,
∴OH=BD=OB,
∴∠OHB=∠OBH,
∴∠HOB=180°﹣2∠OBH,
∵∠OAB=∠CAD=35°,
∴∠ABO=90°﹣35°=55°,
∴∠HOB=180°﹣2×55°=70°.
故答案为:70°.
21.解:以AD、BD为边作矩形ADBE,连接CE、DE,如图所示:
则AB=DE,
由题意得:CD2+CE2=CA2+CB2,
即22+CE2=42+62,
解得:CE=4,
当C、D、E三点共线时,DE最小,
∴AB的最小值=DE的最小值=CE﹣CD=4﹣2;
故答案为:4﹣2.
22.解:∵△ODE是等边三角形,
∴OD=OE,∠ODE=60°,
∵四边形ABCO是正方形,
∴∠AOC=∠BAO=90°,
∴∠AOD=30°,
∴AD=OD,
∵点B的坐标为(3,3),
∴OA=3,
∴32+OD2=OD2,
解得:OD=2,
∴OE=2,
∴点E的坐标为(2,0),
故答案为:(2,0).
23.解:∵四边形ABCD为正方形,
∴∠C=90°,∠CDB=45°,BC=CD.
∴EC⊥CB.
又∵BE平分∠CBD,EF⊥BD,
∴EC=EF.
∵∠CDB=45°,EF⊥BD,
∴△DEF为等腰直角三角形.
∵DE=,
∴EF=1.
∴EC=1.
∴BC=CD=DE+EC=+1.
故答案为:+1.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形;
(2)解:连接AC,如图所示:
∵CE=2BE=4,
∴BE=2,
∴BC=BE+CE=6,
由(1)得:四边形ABCD是菱形,
∴AC⊥BD,AB=BC=6,
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∴AE===4,
∴AC===4,
∵菱形ABCD的面积=AC×BD=BC×AE,
∴BD===4.
25.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB,
∴AB=CB,
∴?ABCD是菱形.
(2)解:由(1)得:?ABCD是菱形,
∴BC=AB=5,AO=CO,
∵AD∥BC,
∴∠AFE=∠CBE,
∵AE=AF=3,
∴∠AFE=∠AEF,
又∵∠AEF=∠CEB,
∴∠CBE=∠CEB,
∴CE=BC=5,
∴AC=AE+CE=3+5=8,
∴AO=AC=4.
26.(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
∵EA⊥AO,DE⊥DO,
∴∠EAO=∠DOA=90°,
∴四边形AODE是矩形;
(2)解:由(1)知,四边形AODE是矩形,
∴∠AED=90°,OA=DE,OD=AE,
∵四边形AODE的面积为12,
∴OA?OD=12,
在Rt△AOD中,根据勾股定理,得OA2+OD2=AD2=25,
∴(OA+OD)2=OA2+2OA?OD+OD2=25+24=49,
∴OA+OD=7,
∴四边形AODE的周长为2(OA+OD)=14.
27.解:(1)∵四边形ABCD是矩形,
∴CD∥AB,
∴∠OCE=∠OAF,
∵点O为对角线AC的中点,
∴CO=AO,
在△COE和△AOF中,
,
∴△COE≌△AOF(ASA);
(2)四边形AECF为菱形,理由:
∵△COE≌△AOF,
∴CE=AF,
又∵CE∥AF,
∴四边形AECF是平行四边形,
∵CD∥AB,
∴∠DEA=∠BAE,
又∵∠DEA=2∠CAB,
∴∠BAE=2∠CAB,
即∠BAC=∠EAC,
∵CD∥AB,
∴∠BAC=∠ACE,
∴∠CAE=∠ACE,
∴AE=CE,
∴四边形AECF是菱形.
28.(1)证明:∵四边形ABCD是平行四边形,
∴AC=2AO,BD=2BO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD为矩形;
(2)解:过点E作EG⊥BD于点G,如图所示:
∵四边形ABCD是矩形,OC=5,
∴∠BAD=90°,BD=AC=2OC=10.
在Rt△ABD中,AB=8,BD=10,
∴AD===6,
∵∠DAB=90°,
∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,
∴EG=EA,∠EGB=90°.
在Rt△ADE和Rt△GDE中,
,
∴Rt△ADE≌Rt△GDE(HL),
∴AD=GD=6,
∴BG=BD﹣GD=10﹣6=4,
在Rt△BEG中,由勾股定理得:BE2=EG2+BG2,
即(8﹣AE)2=AE2+42,
解得:AE=3.
29.解:(1)证明:∵四边形ABCD与四边形CFGM都是正方形,
∴∠BCM=∠FCD=90°,BC=CD,CM=CF.
在△BCM和△DCF中,
,
∴△BCM≌△DCF(SAS).
∴DF=BM,∠CFD=∠CMB.
∵∠BMC+∠CBM=90°,
∴∠CBM+∠CFD=90°,
∴∠BEF=90°,
∴DF⊥BM;
(2)①成立.
∵四边形ABCD与四边形CFGM都是正方形,
∴∠BCM=∠FCD=90°,BC=CD,CM=CF.
在△BCM和△DCF中,
,
∴△BCM≌△DCF(SAS).
∴DF=BM,∠CFD=∠CMB.
∵∠BMC+∠CBM=90°,
∴∠CBM+∠CFD=90°,
∴∠BEF=90°,
∴DF⊥BM;
②设正方形ABCD的边长为x,则BC=CD=x,
∴BD==x,
∵正方形CFGM的边长为1,
∴BF=BC+CF=x+1.
∵BD=BF,
∴x=x+1,
∴x=+1.
∴4x=4+4.
∴正方形ABCD的周长为4+4.
30.解:(1)证明:∵四边形ABCD是正方形,
∴∠D=∠ECQ=90°,
∵E是边CD的中点,
∴DE=CE,
又∵∠DEP=∠CEQ,
∴△PDE≌△QCE(ASA);
(2)①证明:∵PB=PQ,
∴∠PBQ=∠Q,
∵在正方形ABCD中,AD∥BC,
∴∠APB=∠PBQ=∠Q=∠EPD,
∵△PDE≌△QCE,
∴PE=QE,
∵点F是BP的中点,∠PAB=90°,
∴AF=PF=BF,EF∥BQ,
∴∠APF=∠PAF,
∴∠PAF=∠EPD,
∴PE∥AF,
又∵EF∥BQ∥AD,
∴四边形AFEP是平行四边形;
②设AP=x,则PD=1﹣x,
∴CQ=1﹣x,
∴BQ=2﹣x.
∵EF是△PBQ的中位线,
∴EF=(2﹣x),
∵四边形AFEP是平行四边形,
∴EF=AP,
∴(2﹣x)=x,
∴x=.
在Rt△PDE中,DE=,PD2+DE2=PE2,
∴+=PE2,
∴PE=.
31.解:(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在Rt△ABE和Rt△DAF中,
,
∴Rt△ABE≌Rt△DAF(HL);
(2)证明:∵Rt△ABE≌Rt△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∴BE⊥AF;
(3)∵BE⊥AF,
∵点H为BF的中点,
∴GH=BF,
∵在Rt△BCF中,BC=5,CF=CD﹣DF=5﹣2=3,根据勾股定理,得
∴BF==,
∴GH=.
1.如图,在平行四边形ABCD中,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE,添加一个条件,使四边形AEBD是菱形,这个条件是( )
A.∠BAD=∠BDA
B.AB=DE
C.DF=EF
D.∠BDC=∠BAD
2.如图,已知大矩形ABCD由①②③④四个小矩形组成,其中AE=CG,则只需要知道其中一个小矩形的面积就可以求出图中阴影部分的面积,这个小矩形是( )
A.①
B.②
C.③
D.④
3.如图,在矩形ABCD中,点A的坐标是(1,0),点C的坐标是(﹣2,4),则BD的长是( )
A.
B.5
C.3
D.4
4.在平面直角坐标系中,菱形ABCD的顶点的坐标A、B、C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为( )
A.(0,﹣1)
B.(﹣2,1)
C.(2,1)
D.(0,﹣2)
5.如图,矩形ABCD和矩形CEFG,AB=1,BC=CG=2,CE=4,点P在边GF上,点Q在边CE上,且PF=CQ,连接AC和PQ,M,N分别是AC,PQ的中点,则MN的长为( )
A.3
B.6
C.
D.
6.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为( )
A.4
B.8
C.
D.6
7.如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:
①DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.
其中,正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
8.如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )
A.13
B.10
C.12
D.5
9.如图,正方形ABCD中,AB=,点E是对角线AC上一点,EF⊥AB于点F,连接DE,当∠ADE=22.5°时,EF的长是( )
A.1
B.2﹣2
C.﹣1
D.
10.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4
B.2
C.
D.2
11.如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为( )
A.15°
B.22.5°
C.25°
D.17.5°
12.如图,已知菱形ABCD的顶点A(﹣,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A→……的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标是
.
13.如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB,若DC=5,则AF的长为
.
14.有两个全等矩形纸条,长与宽分别为8和6,按图所示交叉叠放在一起,则重合部分构成的四边形面积为
.
15.如图,在△ABC中,已知∠ACB=90°,∠A=30°,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=
时,平行四边形CDEB为菱形.
16.如图,在矩形ABCD中,AB=4,BD=4,对角线AC、BD相交于点O,过点O作OE⊥AC交BC于点E,则CE的长是
.
17.如图,已知在△ABC中,∠C=25°,点D在边BC上,且∠DAC=90°,AB=DC.则∠BAC的度数为
°.
18.矩形ABCD中,AB=5,BC=4,E、F分别在AB、CD上,且EF垂直平分AC.则AE的长为
.
19.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B点的纵坐标是
.
20.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=35°,则∠HOB的度数为
.
21.学习新知:如图1、图2,P是矩形ABCD所在平面内任意一点,则有以下重要结论:AP2+CP2=BP2+DP2.该结论的证明不难,同学们通过勾股定理即可证明.
应用新知:如图3,在△ABC中,CA=4,CB=6,D是△ABC内一点,且CD=2,∠ADB=90°,则AB的最小值为
.
22.如图,在平面直角坐标中,D是正方形ABCO的边AB上一点,以OD为边的等边△ODE,点E在x轴正半轴上,若点B的坐标为(3,3),则点E的坐标为
.
23.如图,在正方形ABCD中,BE平分∠CBD,EF⊥BD于点F.若DE=,则BC的长为
.
24.如图所示,平行四边形ABCD,对角线BD平分∠ABC;
(1)求证:四边形ABCD为菱形;
(2)已知AE⊥BC于E,若CE=2BE=4,求BD.
25.如图,已知?ABCD的对角线AC、BD交于点O,且∠1=∠2.
(1)求证:?ABCD是菱形.
(2)F为AD上一点,连接BF交AC于E,且AE=AF,若AF=3,AB=5,求AO的长.
26.如图,已知菱形ABCD的对角线AC、BD相交于点O,分别过A、D两点作AO、DO的垂线,两垂线交于点E.
(1)求证:四边形AODE是矩形;
(2)若四边形AODE的面积为12,AD=5,求四边形AODE的周长.
27.如图,在矩形ABCD中,点O为对角线AC的中点,点E是CD上一点,连接EO并延长交AB于点F,连接AE、CF.
(1)求证:△COE≌△AOF;
(2)当∠DEA=2∠CAB时,试判断四边形AECF的形状,并说明理由.
28.如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
29.正方形ABCD中,M为射线CD上一点(不与D重合),以CM为边,在正方形ABCD的异侧作正方形CFGM,连接BM,DF,直线BM与DF交于点E.
(1)如图1,若M在CD的延长线上,求证:DF=BM,DF⊥BM;
(2)如图2,若M移到边CD上.
①在(1)中结论是否仍成立?(直接回答不需证明)
②连接BD,若BD=BF,且正方形CFGM的边长为1,试求正方形ABCD的周长.
30.如图,在边长为1的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:△PDE≌△QCE;
(2)若PB=PQ,点F是BP的中点,连接EF、AF,
①求证:四边形AFEP是平行四边形;②求PE的长.
31.如图,已知四边形ABCD是正方形,点E、F分别在AD、DC上,BE与AF相交于点G,且BE=AF.
(1)求证:△ABE≌△DAF;
(2)求证:BE⊥AF;
(3)如果正方形ABCD的边长为5,AE=2,点H为BF的中点,连接GH.求GH的长.
参考答案
1.解:添加一个条件∠BDC=∠BAD,使四边形AEBD是菱形;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∠BAD=∠C,
∴AD∥BE,
∴∠ADF=∠BEF,
∵点F是AB的中点,
∴AF=BF,
在△ADF和△BEF中,,
∴△ADF≌△BEF(AAS),
∴AD=BE,
又∵AD∥BE,
∴四边形AEBD是平行四边形,
∵∠BDC=∠BAD,∠BAD=∠C,
∴∠BDC=∠C,
∴BD=BC,
∵AD=BC,AD=BE,
∴BD=BE,
∴四边形AEBD是菱形;
故选:D.
2.解:如图所示:
∵四边形ABCD和四边形③是矩形,
∴AB=CD,FP=CG,
∵AE=CG,
∴BE=DG,
∴阴影部分的面积=△BFD的面积﹣△BFP的面积=BF×CD﹣BF×FP=BF×(CD﹣CG)=BF×DG=BF×BE=矩形②面积,
故选:B.
3.解:连接AC,如图:
∵四边形ABCD是矩形,
∴BD=AC,
∵点A的坐标是(1,0),点C的坐标是(﹣2,4),
∴AC==5,
∴BD=AC=5,
故选:B.
4.解:如图所示,
∵菱形ABCD的对角线互相垂直平分,A、B、C分别为(﹣2,0),(0,1),(2,0),
∴D(0,﹣1).
故选:A.
5.解:连接CF,交PQ于R,延长AD交EF于H,连接AF,如图所示:
则四边形ABEH是矩形,
∴HE=AB=1,AH=BE=BC+CE=2+4=6,
∵四边形CEFG是矩形,
∴FG∥CE,EF=CG=2,
∴∠RFP=∠RCQ,∠RPF=∠RQC,FH=EF﹣HE=2﹣1=1,
在Rt△AHF中,由勾股定理得:AF===,
在△RFP和△RCQ中,,
∴△RFP≌△RCQ(ASA),
∴RP=RQ,
∴点R与点M重合,
∵点N是AC的中点,
∴MN是△CAF的中位线,
∴MN=AF=×=,
故选:C.
6.解:∵四边形ABCD是菱形,
∴OA=OC=6,OB=OD,AC⊥BD,
∴AC=12,
∵DH⊥AB,
∴∠BHD=90°,
∴OH=BD,
∵菱形ABCD的面积=×AC×BD=×12×BD=48,
∴BD=8,
∴OH=BD=4;
故选:A.
7.解:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∠DAE=∠BCF=90°,OD=OB=OA=OC,AD=BC,AD∥BC,
∴∠DAN=∠BCM,
∵BF⊥AC,DE∥BF,
∴DE⊥AC,
∴∠DNA=∠BMC=90°,
在△DNA和△BMC中,,
∴△DNA≌△BMC(AAS),
∴DN=BM,∠ADE=∠CBF,故①正确;
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA),
∴AE=FC,DE=BF,故③正确;
∴DE﹣DN=BF﹣BM,即NE=MF,
∵DE∥BF,
∴四边形NEMF是平行四边形,
∴EM∥FN,故②正确;
∵AB=CD,AE=CF,
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵AO=AD,
∴AO=AD=OD,
∴△AOD是等边三角形,
∴∠ADO=∠DAN=60°,
∴∠ABD=90°﹣∠ADO=30°,
∵DE⊥AC,
∴∠ADN=ODN=30°,
∴∠ODN=∠ABD,
∴DE=BE,
∴四边形DEBF是菱形;故④正确;
正确结论的个数是4个,
故选:D.
8.解:连接BD,交AC于点O,如图:
∵菱形ABCD的边长为13,点E、F分别是边CD、BC的中点,
∴AB∥CD,AB=BC=CD=DA=13,EF∥BD,
∵AC、BD是菱形的对角线,AC=24,
∴AC⊥BD,AO=CO=12,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∴四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,∵OC⊥OD,CD=13,CO=12,
∴OB=OD==5,
∴BD=2OD=10,
∴EG=BD=10;
故选:B.
9.解:∵四边形ABCD是正方形,
∴AB=CD=BC=,∠B=∠ADC=90°,∠BAC=∠CAD=45°,
∴AC=AB=2,
∵∠ADE=22.5°,
∴∠CDE=90°﹣22.5°=67.5°,
∵∠CED=∠CAD+∠ADE=45°+22.5°=67.5°,
∴∠CDE=∠CED,
∴CD=CE=,
∴AE=2﹣,
∵EF⊥AB,
∴∠AFE=90°,
∴△AFE是等腰直角三角形,
∴EF==﹣1,
故选:C.
10.解:在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,
∴OA=AC==.
故选:C.
11.解:∵四边形ABCD是正方形,
∴∠BOC=90°,∠OBC=45°,
∵BP=OB,
∴∠BOP=∠BPO=(180°﹣45°)=67.5°,
∴∠COP=90°﹣67.5°=22.5°.
故选:B.
12.解:∵在菱形ABCD中,∠DAB=60°,
∴∠OAD=30°,
∵A(﹣,0)
∴在Rt△AOD中,OA=,
∴OD=OA?tan30°=1,
∴AD=2,
∵动点P绕菱形一周的时间为2×4÷0.5=16(秒),
又2020÷16=126…4,
∴第2020秒时,点P运动到点B处,
∵OB=OD=1,
∴此时点P的坐标为(0,﹣1).
故答案为:(0,﹣1).
13.解:∵AD∥BC,DE⊥BC,
∴AD⊥DE,∠GAD=∠ACB,
∴∠ADF=90°,
∵点G为AF的中点,
∴DG=AF=GA,
∴∠GAD=∠GDA,
∴∠DGC=∠GAD+∠GDA=2∠GAD,
∵AD∥BC,
∴∠GAD=∠ACB,
∵∠ACD=2∠ACB,
∴∠DGC=∠ACD,
∴DG=DC=5,
∴AF=10,
故答案为:10.
14.解:如图所示:
由题意得:矩形ABCD≌矩形BEDF,
∴∠A=90°,AB=BE=6,AD∥BC,BF∥DE,AD=8,
∴四边形BGDH是平行四边形,
∴平行四边形BGDH的面积=BG×AB=BH×BE,
∴BG=BH,
∴四边形BGDH是菱形,
∴BH=DH,
设BH=DH=x,则AH=8﹣x,
在Rt△ABH中,由勾股定理得:62+(8﹣x)2=x2,
解得:x=,
∴BG=,
∴四边形BGDH的面积=BG×AB=×6=;
故答案为:.
15.解:连接CE交AB于点O,如图所示:
∵Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,
∴AB=2BC=12,AC===6,
若平行四边形CDEB为菱形时,CE⊥BD,OD=OB,CD=CB,
∵AB?OC=AC?BC,
∴OC===3,
∴OB===3,
∴AD=AB﹣2OB=12﹣2×3=6,
故答案为:6.
16.解:如图,连接AE,
∵在矩形ABCD中,OA=OC,OE⊥AC,
∴OE垂直平分AC,
∴AE=CE,
∵∠BAD=90°,AB=4,BD=4,
∴AD=BC==8,
∴BE=BC﹣CE=8﹣CE,
∴在Rt△ABE中,根据勾股定理,得
AE2=AB2+BE2,
即CE2=42+(8﹣CE)2,
解得CE=5.
故答案为:5.
17.解:取CD的中点E,连接AE,
在Rt△ADC中,DE=EC,
∴AE=CD=ED=EC,
∴∠EAC=∠C=25°,
∴∠AED=∠EAC+∠C=50°,
∵AE=ED,
∴∠EAD=∠EDA=65°,
∵AB=DC,AE=CD,
∴AB=AE,
∴∠BAE=80°,
∴∠BAC=∠BAE+∠EAC=105°,
故答案为:105.
18.解:如图,连接CE,
∵EF垂直平分AC,
∴CE=AE,
则BE=AB﹣AE=5﹣AE,
∵矩形ABCD中,∠B=90°,
在Rt△CBE中,根据勾股定理,得
CE2=BE2+BC2,
即:AE2=(5﹣AE)2+42,
解得AE=4.1.
答:AE的长为4.1.
故答案为:4.1.
19.解:如图,
过点A作AD⊥x轴于点D,
过点B作BE⊥x轴于点E,
过点C作CF∥y轴,过点A作AF∥x轴,交点为F,
则AF⊥CF,
延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴OB=AC,AC∥OB,
∴∠CAF=∠CHO=∠BOE,
∵∠AFC=∠OEB=90°,
∴△AFC≌△OEB(AAS),
∴CF=BE=4﹣1=3,
故答案为:3.
20.解:∵四边形ABCD是菱形,
∴BO=DO,
∵DH⊥AB,
∴∠DHB=90°,
∴OH=BD=OB,
∴∠OHB=∠OBH,
∴∠HOB=180°﹣2∠OBH,
∵∠OAB=∠CAD=35°,
∴∠ABO=90°﹣35°=55°,
∴∠HOB=180°﹣2×55°=70°.
故答案为:70°.
21.解:以AD、BD为边作矩形ADBE,连接CE、DE,如图所示:
则AB=DE,
由题意得:CD2+CE2=CA2+CB2,
即22+CE2=42+62,
解得:CE=4,
当C、D、E三点共线时,DE最小,
∴AB的最小值=DE的最小值=CE﹣CD=4﹣2;
故答案为:4﹣2.
22.解:∵△ODE是等边三角形,
∴OD=OE,∠ODE=60°,
∵四边形ABCO是正方形,
∴∠AOC=∠BAO=90°,
∴∠AOD=30°,
∴AD=OD,
∵点B的坐标为(3,3),
∴OA=3,
∴32+OD2=OD2,
解得:OD=2,
∴OE=2,
∴点E的坐标为(2,0),
故答案为:(2,0).
23.解:∵四边形ABCD为正方形,
∴∠C=90°,∠CDB=45°,BC=CD.
∴EC⊥CB.
又∵BE平分∠CBD,EF⊥BD,
∴EC=EF.
∵∠CDB=45°,EF⊥BD,
∴△DEF为等腰直角三角形.
∵DE=,
∴EF=1.
∴EC=1.
∴BC=CD=DE+EC=+1.
故答案为:+1.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形;
(2)解:连接AC,如图所示:
∵CE=2BE=4,
∴BE=2,
∴BC=BE+CE=6,
由(1)得:四边形ABCD是菱形,
∴AC⊥BD,AB=BC=6,
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∴AE===4,
∴AC===4,
∵菱形ABCD的面积=AC×BD=BC×AE,
∴BD===4.
25.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB,
∴AB=CB,
∴?ABCD是菱形.
(2)解:由(1)得:?ABCD是菱形,
∴BC=AB=5,AO=CO,
∵AD∥BC,
∴∠AFE=∠CBE,
∵AE=AF=3,
∴∠AFE=∠AEF,
又∵∠AEF=∠CEB,
∴∠CBE=∠CEB,
∴CE=BC=5,
∴AC=AE+CE=3+5=8,
∴AO=AC=4.
26.(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
∵EA⊥AO,DE⊥DO,
∴∠EAO=∠DOA=90°,
∴四边形AODE是矩形;
(2)解:由(1)知,四边形AODE是矩形,
∴∠AED=90°,OA=DE,OD=AE,
∵四边形AODE的面积为12,
∴OA?OD=12,
在Rt△AOD中,根据勾股定理,得OA2+OD2=AD2=25,
∴(OA+OD)2=OA2+2OA?OD+OD2=25+24=49,
∴OA+OD=7,
∴四边形AODE的周长为2(OA+OD)=14.
27.解:(1)∵四边形ABCD是矩形,
∴CD∥AB,
∴∠OCE=∠OAF,
∵点O为对角线AC的中点,
∴CO=AO,
在△COE和△AOF中,
,
∴△COE≌△AOF(ASA);
(2)四边形AECF为菱形,理由:
∵△COE≌△AOF,
∴CE=AF,
又∵CE∥AF,
∴四边形AECF是平行四边形,
∵CD∥AB,
∴∠DEA=∠BAE,
又∵∠DEA=2∠CAB,
∴∠BAE=2∠CAB,
即∠BAC=∠EAC,
∵CD∥AB,
∴∠BAC=∠ACE,
∴∠CAE=∠ACE,
∴AE=CE,
∴四边形AECF是菱形.
28.(1)证明:∵四边形ABCD是平行四边形,
∴AC=2AO,BD=2BO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD为矩形;
(2)解:过点E作EG⊥BD于点G,如图所示:
∵四边形ABCD是矩形,OC=5,
∴∠BAD=90°,BD=AC=2OC=10.
在Rt△ABD中,AB=8,BD=10,
∴AD===6,
∵∠DAB=90°,
∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,
∴EG=EA,∠EGB=90°.
在Rt△ADE和Rt△GDE中,
,
∴Rt△ADE≌Rt△GDE(HL),
∴AD=GD=6,
∴BG=BD﹣GD=10﹣6=4,
在Rt△BEG中,由勾股定理得:BE2=EG2+BG2,
即(8﹣AE)2=AE2+42,
解得:AE=3.
29.解:(1)证明:∵四边形ABCD与四边形CFGM都是正方形,
∴∠BCM=∠FCD=90°,BC=CD,CM=CF.
在△BCM和△DCF中,
,
∴△BCM≌△DCF(SAS).
∴DF=BM,∠CFD=∠CMB.
∵∠BMC+∠CBM=90°,
∴∠CBM+∠CFD=90°,
∴∠BEF=90°,
∴DF⊥BM;
(2)①成立.
∵四边形ABCD与四边形CFGM都是正方形,
∴∠BCM=∠FCD=90°,BC=CD,CM=CF.
在△BCM和△DCF中,
,
∴△BCM≌△DCF(SAS).
∴DF=BM,∠CFD=∠CMB.
∵∠BMC+∠CBM=90°,
∴∠CBM+∠CFD=90°,
∴∠BEF=90°,
∴DF⊥BM;
②设正方形ABCD的边长为x,则BC=CD=x,
∴BD==x,
∵正方形CFGM的边长为1,
∴BF=BC+CF=x+1.
∵BD=BF,
∴x=x+1,
∴x=+1.
∴4x=4+4.
∴正方形ABCD的周长为4+4.
30.解:(1)证明:∵四边形ABCD是正方形,
∴∠D=∠ECQ=90°,
∵E是边CD的中点,
∴DE=CE,
又∵∠DEP=∠CEQ,
∴△PDE≌△QCE(ASA);
(2)①证明:∵PB=PQ,
∴∠PBQ=∠Q,
∵在正方形ABCD中,AD∥BC,
∴∠APB=∠PBQ=∠Q=∠EPD,
∵△PDE≌△QCE,
∴PE=QE,
∵点F是BP的中点,∠PAB=90°,
∴AF=PF=BF,EF∥BQ,
∴∠APF=∠PAF,
∴∠PAF=∠EPD,
∴PE∥AF,
又∵EF∥BQ∥AD,
∴四边形AFEP是平行四边形;
②设AP=x,则PD=1﹣x,
∴CQ=1﹣x,
∴BQ=2﹣x.
∵EF是△PBQ的中位线,
∴EF=(2﹣x),
∵四边形AFEP是平行四边形,
∴EF=AP,
∴(2﹣x)=x,
∴x=.
在Rt△PDE中,DE=,PD2+DE2=PE2,
∴+=PE2,
∴PE=.
31.解:(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在Rt△ABE和Rt△DAF中,
,
∴Rt△ABE≌Rt△DAF(HL);
(2)证明:∵Rt△ABE≌Rt△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∴BE⊥AF;
(3)∵BE⊥AF,
∵点H为BF的中点,
∴GH=BF,
∵在Rt△BCF中,BC=5,CF=CD﹣DF=5﹣2=3,根据勾股定理,得
∴BF==,
∴GH=.
