2020-2021学年八年级数学人教版下册18.2.1.1矩形的性质课件(共41张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册18.2.1.1矩形的性质课件(共41张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 545.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览









文档简介
(共41张PPT)
18.2.1.1
矩形的性质
学习目标
1
2
3
掌握矩形的性质及推论,能运用其解决相关问题
发展初步的合理推理能力和数学表达能力
理解矩形与平行四边形的区别和联系,体会一般和特殊的辨证关系
学习重难点
重点
难点
掌握矩形的性质
运用矩形的性质解决相关问题
长方形也叫矩形,是生活中常见的图形.
提出问题,引发思考
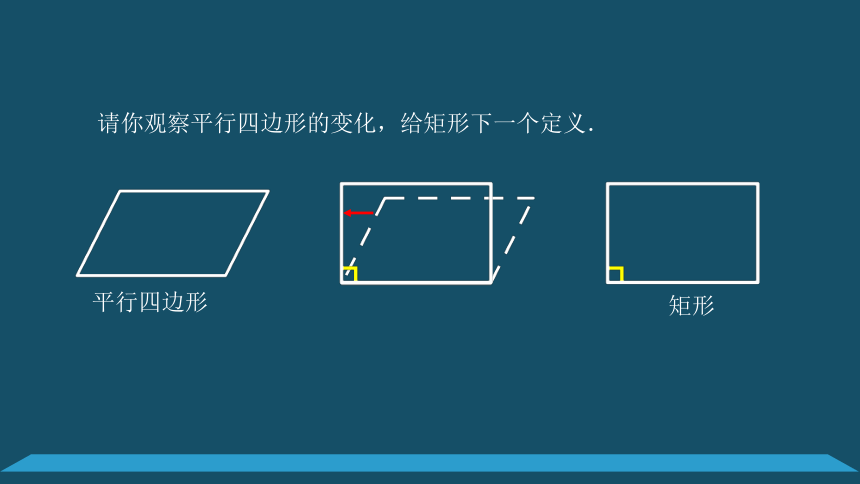
平行四边形
请你观察平行四边形的变化,给矩形下一个定义.
矩形
平行四边形
矩形
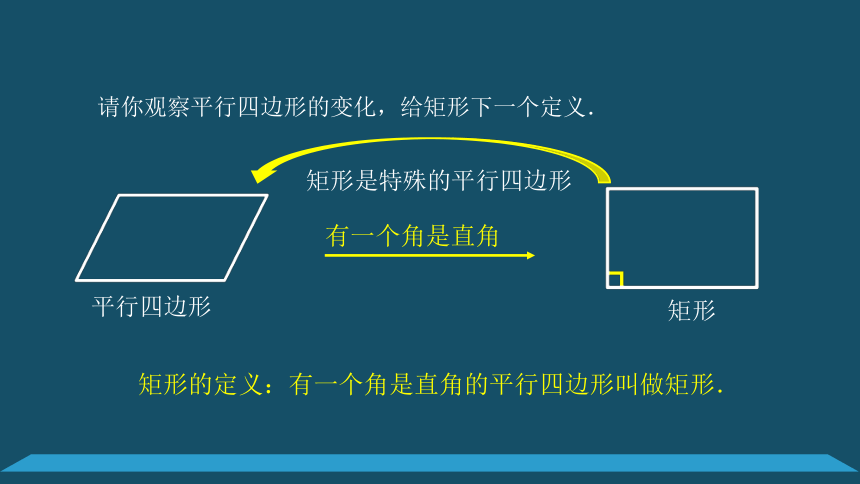
有一个角是直角
矩形的定义:有一个角是直角的平行四边形叫做矩形.
矩形是特殊的平行四边形
请你观察平行四边形的变化,给矩形下一个定义.
如图,记作矩形ABCD.
D
C
B
A
矩形的定义:
有一个角是直角的平行四边形叫做矩形.
∵四边形ABCD是平行四边形,
∠B=90°,
∴□ABCD是矩形.
∵
四边形ABCD是矩形,
∴
四边形ABCD是平行四边形,∠B=90°.
D
C
B
A
矩形的定义:
有一个角是直角的平行四边形叫做矩形.
平行四边形
性质
边
角
对角线
探究性质,深化认知
对边平行且相等
对角相等、邻角互补
对角线互相平分
矩形
性质
边
角
对角线
对边平行且相等
对角相等、邻角互补
对角线互相平分
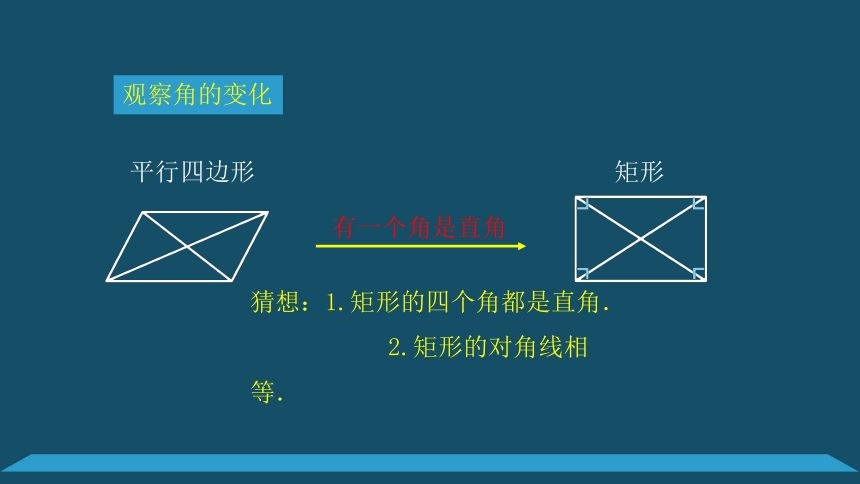
观察边、角、对角线
猜想矩形具有哪些一般平行四边形不具有的特殊性质.
平行四边形
矩形
有一个角是直角
有一个角是直角
观察角的变化
平行四边形
矩形
猜想:1.矩形的四个角都是直角.
2.矩形的对角线相等.
AD∥BC
分析:
∠A=∠C,
∠D=∠B
∠A=90°
∠A+∠B=180°
D
C
B
A
四边形ABCD是矩形
□ABCD
∠B=90°
∠D=∠B=90°
猜想1
矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
证明:∵
四边形ABCD
是矩形,
不妨设∠B=90°,
∴
∠A=∠C,∠D=∠B=90°,
AD∥BC.
∴
∠A+∠B=180°.
∴
∠A=180°-∠B=90°
.
∴
∠C=∠A=90°.
∴
∠A=∠B=∠C=∠D=90°.
D
C
B
A
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
矩形的性质:矩形的四个角都是直角.
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
D
C
B
A
A
B
C
D
分析:
AB=CD
∠ABC=∠DCB=90°
△ABC≌△DCB
AC=BD
四边形ABCD是矩形
BC=CB
猜想2
矩形的对角线相等.
已知:如图,四边形ABCD是矩形,AC,BD是矩形ABCD的对角线.
求证:AC=BD
.
证明:∵四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°.
又BC=CB,
∴△ABC≌△DCB.
∴AC=BD.
方法一
A
B
C
D
已知:如图,四边形ABCD是矩形,AC,BD是矩形ABCD的对角线.
求证:AC=BD
.
分析:
AB=CD
∠ABC=∠DCB=90°
AC=BD
四边形ABCD是矩形
在Rt△ABC中,AC2=AB2+BC2
在Rt△DCB中,BD2=CD2+BC2
A
B
C
D
已知:如图,四边形ABCD是矩形,AC,BD是矩形ABCD的对角线.
求证:AC=BD
.
证明:∵
四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°.
∴在Rt△ABC中,AC2=AB2+BC2,
在Rt△DCB中,BD2=CD2+BC2.
∴AC2=BD2
.
∴AC=BD.
方法二
已知:如图,四边形ABCD是矩形,AC,BD是矩形ABCD的对角线.
求证:AC=BD
.
A
B
C
D
矩形的性质:
矩形的对角线相等且互相平分.
∵
四边形ABCD是矩形,
∴
OA=OB=OC=OD.
A
B
C
D
矩形不同于平行四边形的特殊性质:
矩形的四个角都是直角;
矩形的对角线相等.
矩形
性质
边
角
对角线
矩形是特殊的平行四边形
对边平行且相等
四个角都是直角
对角线相等且互相平分
边
角
对角线
对边平行且相等
四个角都是直角
对角线相等且互相平分
性质
平行四边形
矩形
角特殊化
一般
特殊
例1
矩形对角线组成的对顶角中,有一组是两个50°的角,对角线与各边组成的角是多少度?
如图,四边形ABCD是矩形,
对角线AC,BD交于点O,∠AOB=∠COD=50°.
1
2
3
4
5
6
7
8
A
B
C
D
O
四边形ABCD是矩形
分析:
OA=OB=OC=OD
∠1=∠2,∠3=∠4
∠5=∠6,∠7=∠8
∠1=∠2=∠5=∠6
∠3=∠4=∠7=∠8
AB∥DC,AD∥BC
∠1=∠5,
∠3=∠7
如图,四边形ABCD是矩形,对角线AC,BD交于点O,∠AOB=∠COD=50°.
1
2
3
4
5
6
7
8
A
B
C
D
O
∠1=∠2=65°
∠3=90°-∠2=25°
∠AOB=50°
∠ABC=90°
OA=OB
四边形ABCD是矩形
如图,四边形ABCD是矩形,对角线AC,BD交于点O,∠AOB=∠COD=50°.
分析:
1
2
3
4
5
6
7
8
A
B
C
D
O
答:对角线与各边组成的角是65°和25°.
例1
矩形对角线组成的对顶角中,有一组是两个50°的角,对角线与各边组成的角是多少度?
A
B
C
D
O
例2
如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
BC
∠ACB=30°
AC=2AB=8
OB=OC
四边形ABCD是矩形
A
B
C
D
O
分析:
∠ABC=90°
30°
AB2+BC2=AC2
解
:∵四边形ABCD是矩形,
∴OA=OB,∠ABC=90°.
∵∠AOB=60°,
∴△OAB是等边三角形.
∴OA=AB=4.
∴AC=2OA=8.
A
B
C
D
O
例2
如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
∵∠ABC=90°,∴△ABC是直角三角形.
在Rt△ABC中,AB2+BC2=AC2,
∴BC=
.
等腰三角形
直角三角形
等边三角形
含30°角的直角三角形
A
B
C
D
O
60°
例题小结
A
B
C
D
O
等腰三角形
全等三角形
直角三角形
(等边三角形)
A
B
C
D
O
A
B
C
D
O
全等三角形
特
殊
化
三角形
平行四边形
矩形
直角三角形
平行四边形与三角形的联系
A
B
C
D
O
A
B
C
O
在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系吗?
探究直角三角形的性质
矩形ABCD
Rt△ABC
直角三角形斜边上的中线等于斜边的一半.
A
B
C
O
∵
OA=OC,DO=BO,
∴四边形ABCD是平行四边形.
又∠ABC=90°,∴□ABCD是矩形.
∴AC=BD.又
,
∴
.
证明:延长BO至点D,使得DO=BO,连接AD,CD.
D
已知:如图,在Rt△ABC中,∠ABC=90°,BO是斜边AC上的中线.
求证:
A
B
C
O
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
∵
在Rt△ABC中,∠ABC=90°,
BO是斜边AC上的中线,
∴
解:∵∠ACD=3∠BCD,∠ACB=90°,
∴∠ACD=67.5°.
又CD⊥AB,
∴∠A=90°-∠ACD=22.5°.
∵∠ACB=90°,点E是斜边AB的中点,
∴AE=CE.
∴∠ECA=∠A=22.5°.
∴∠ECD=∠ACD-∠ECA=45°.
C
A
E
D
B
练习
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,
∠ACD=3∠BCD,E是斜边AB的中点,∠ECD是多少度?
矩形是轴对称图形吗?如果是,它的对称轴是什么?
矩形是轴对称图形.
对称轴是对边中点连线所在的直线.
探究矩形的轴对称性
课堂总结
构
造
转
化
直角
直角
平行四边形
三角形
矩形
直角三角形
构
造
转
化
课后作业
1.一个矩形的一条对角线长为8,两条对角线的一个交角为
120°,求这个矩形的边长(结果保留小数点后两位).
2.在Rt△ABC中,∠C=90°,AB=2AC,求∠A,∠B的度数.
课后作业
C
B
D
O
x
y
3.如图,四边形OBCD是矩形,O,B,D三点的坐标分别为(0,0),(b,0),(0,d),求点C的坐标.
再
见
18.2.1.1
矩形的性质
学习目标
1
2
3
掌握矩形的性质及推论,能运用其解决相关问题
发展初步的合理推理能力和数学表达能力
理解矩形与平行四边形的区别和联系,体会一般和特殊的辨证关系
学习重难点
重点
难点
掌握矩形的性质
运用矩形的性质解决相关问题
长方形也叫矩形,是生活中常见的图形.
提出问题,引发思考
平行四边形
请你观察平行四边形的变化,给矩形下一个定义.
矩形
平行四边形
矩形
有一个角是直角
矩形的定义:有一个角是直角的平行四边形叫做矩形.
矩形是特殊的平行四边形
请你观察平行四边形的变化,给矩形下一个定义.
如图,记作矩形ABCD.
D
C
B
A
矩形的定义:
有一个角是直角的平行四边形叫做矩形.
∵四边形ABCD是平行四边形,
∠B=90°,
∴□ABCD是矩形.
∵
四边形ABCD是矩形,
∴
四边形ABCD是平行四边形,∠B=90°.
D
C
B
A
矩形的定义:
有一个角是直角的平行四边形叫做矩形.
平行四边形
性质
边
角
对角线
探究性质,深化认知
对边平行且相等
对角相等、邻角互补
对角线互相平分
矩形
性质
边
角
对角线
对边平行且相等
对角相等、邻角互补
对角线互相平分
观察边、角、对角线
猜想矩形具有哪些一般平行四边形不具有的特殊性质.
平行四边形
矩形
有一个角是直角
有一个角是直角
观察角的变化
平行四边形
矩形
猜想:1.矩形的四个角都是直角.
2.矩形的对角线相等.
AD∥BC
分析:
∠A=∠C,
∠D=∠B
∠A=90°
∠A+∠B=180°
D
C
B
A
四边形ABCD是矩形
□ABCD
∠B=90°
∠D=∠B=90°
猜想1
矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
证明:∵
四边形ABCD
是矩形,
不妨设∠B=90°,
∴
∠A=∠C,∠D=∠B=90°,
AD∥BC.
∴
∠A+∠B=180°.
∴
∠A=180°-∠B=90°
.
∴
∠C=∠A=90°.
∴
∠A=∠B=∠C=∠D=90°.
D
C
B
A
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
矩形的性质:矩形的四个角都是直角.
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
D
C
B
A
A
B
C
D
分析:
AB=CD
∠ABC=∠DCB=90°
△ABC≌△DCB
AC=BD
四边形ABCD是矩形
BC=CB
猜想2
矩形的对角线相等.
已知:如图,四边形ABCD是矩形,AC,BD是矩形ABCD的对角线.
求证:AC=BD
.
证明:∵四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°.
又BC=CB,
∴△ABC≌△DCB.
∴AC=BD.
方法一
A
B
C
D
已知:如图,四边形ABCD是矩形,AC,BD是矩形ABCD的对角线.
求证:AC=BD
.
分析:
AB=CD
∠ABC=∠DCB=90°
AC=BD
四边形ABCD是矩形
在Rt△ABC中,AC2=AB2+BC2
在Rt△DCB中,BD2=CD2+BC2
A
B
C
D
已知:如图,四边形ABCD是矩形,AC,BD是矩形ABCD的对角线.
求证:AC=BD
.
证明:∵
四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°.
∴在Rt△ABC中,AC2=AB2+BC2,
在Rt△DCB中,BD2=CD2+BC2.
∴AC2=BD2
.
∴AC=BD.
方法二
已知:如图,四边形ABCD是矩形,AC,BD是矩形ABCD的对角线.
求证:AC=BD
.
A
B
C
D
矩形的性质:
矩形的对角线相等且互相平分.
∵
四边形ABCD是矩形,
∴
OA=OB=OC=OD.
A
B
C
D
矩形不同于平行四边形的特殊性质:
矩形的四个角都是直角;
矩形的对角线相等.
矩形
性质
边
角
对角线
矩形是特殊的平行四边形
对边平行且相等
四个角都是直角
对角线相等且互相平分
边
角
对角线
对边平行且相等
四个角都是直角
对角线相等且互相平分
性质
平行四边形
矩形
角特殊化
一般
特殊
例1
矩形对角线组成的对顶角中,有一组是两个50°的角,对角线与各边组成的角是多少度?
如图,四边形ABCD是矩形,
对角线AC,BD交于点O,∠AOB=∠COD=50°.
1
2
3
4
5
6
7
8
A
B
C
D
O
四边形ABCD是矩形
分析:
OA=OB=OC=OD
∠1=∠2,∠3=∠4
∠5=∠6,∠7=∠8
∠1=∠2=∠5=∠6
∠3=∠4=∠7=∠8
AB∥DC,AD∥BC
∠1=∠5,
∠3=∠7
如图,四边形ABCD是矩形,对角线AC,BD交于点O,∠AOB=∠COD=50°.
1
2
3
4
5
6
7
8
A
B
C
D
O
∠1=∠2=65°
∠3=90°-∠2=25°
∠AOB=50°
∠ABC=90°
OA=OB
四边形ABCD是矩形
如图,四边形ABCD是矩形,对角线AC,BD交于点O,∠AOB=∠COD=50°.
分析:
1
2
3
4
5
6
7
8
A
B
C
D
O
答:对角线与各边组成的角是65°和25°.
例1
矩形对角线组成的对顶角中,有一组是两个50°的角,对角线与各边组成的角是多少度?
A
B
C
D
O
例2
如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
BC
∠ACB=30°
AC=2AB=8
OB=OC
四边形ABCD是矩形
A
B
C
D
O
分析:
∠ABC=90°
30°
AB2+BC2=AC2
解
:∵四边形ABCD是矩形,
∴OA=OB,∠ABC=90°.
∵∠AOB=60°,
∴△OAB是等边三角形.
∴OA=AB=4.
∴AC=2OA=8.
A
B
C
D
O
例2
如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求AC与BC的长.
∵∠ABC=90°,∴△ABC是直角三角形.
在Rt△ABC中,AB2+BC2=AC2,
∴BC=
.
等腰三角形
直角三角形
等边三角形
含30°角的直角三角形
A
B
C
D
O
60°
例题小结
A
B
C
D
O
等腰三角形
全等三角形
直角三角形
(等边三角形)
A
B
C
D
O
A
B
C
D
O
全等三角形
特
殊
化
三角形
平行四边形
矩形
直角三角形
平行四边形与三角形的联系
A
B
C
D
O
A
B
C
O
在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系吗?
探究直角三角形的性质
矩形ABCD
Rt△ABC
直角三角形斜边上的中线等于斜边的一半.
A
B
C
O
∵
OA=OC,DO=BO,
∴四边形ABCD是平行四边形.
又∠ABC=90°,∴□ABCD是矩形.
∴AC=BD.又
,
∴
.
证明:延长BO至点D,使得DO=BO,连接AD,CD.
D
已知:如图,在Rt△ABC中,∠ABC=90°,BO是斜边AC上的中线.
求证:
A
B
C
O
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
∵
在Rt△ABC中,∠ABC=90°,
BO是斜边AC上的中线,
∴
解:∵∠ACD=3∠BCD,∠ACB=90°,
∴∠ACD=67.5°.
又CD⊥AB,
∴∠A=90°-∠ACD=22.5°.
∵∠ACB=90°,点E是斜边AB的中点,
∴AE=CE.
∴∠ECA=∠A=22.5°.
∴∠ECD=∠ACD-∠ECA=45°.
C
A
E
D
B
练习
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,
∠ACD=3∠BCD,E是斜边AB的中点,∠ECD是多少度?
矩形是轴对称图形吗?如果是,它的对称轴是什么?
矩形是轴对称图形.
对称轴是对边中点连线所在的直线.
探究矩形的轴对称性
课堂总结
构
造
转
化
直角
直角
平行四边形
三角形
矩形
直角三角形
构
造
转
化
课后作业
1.一个矩形的一条对角线长为8,两条对角线的一个交角为
120°,求这个矩形的边长(结果保留小数点后两位).
2.在Rt△ABC中,∠C=90°,AB=2AC,求∠A,∠B的度数.
课后作业
C
B
D
O
x
y
3.如图,四边形OBCD是矩形,O,B,D三点的坐标分别为(0,0),(b,0),(0,d),求点C的坐标.
再
见
