2020-2021学年八年级数学苏科版下册 9.4矩形 菱形 正方形同步基础培优训练题(Word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学苏科版下册 9.4矩形 菱形 正方形同步基础培优训练题(Word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 00:00:00 | ||
图片预览


文档简介
2020-2021学年苏科版数学八年级下册第九章
9.4矩形
菱形
正方形同步基础培优训练题
一、单选题
1.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是(
)
①平行四边形;②菱形;③任意四边形;④对角线互相垂直的四边形
A.①③
B.②③
C.③④
D.②④
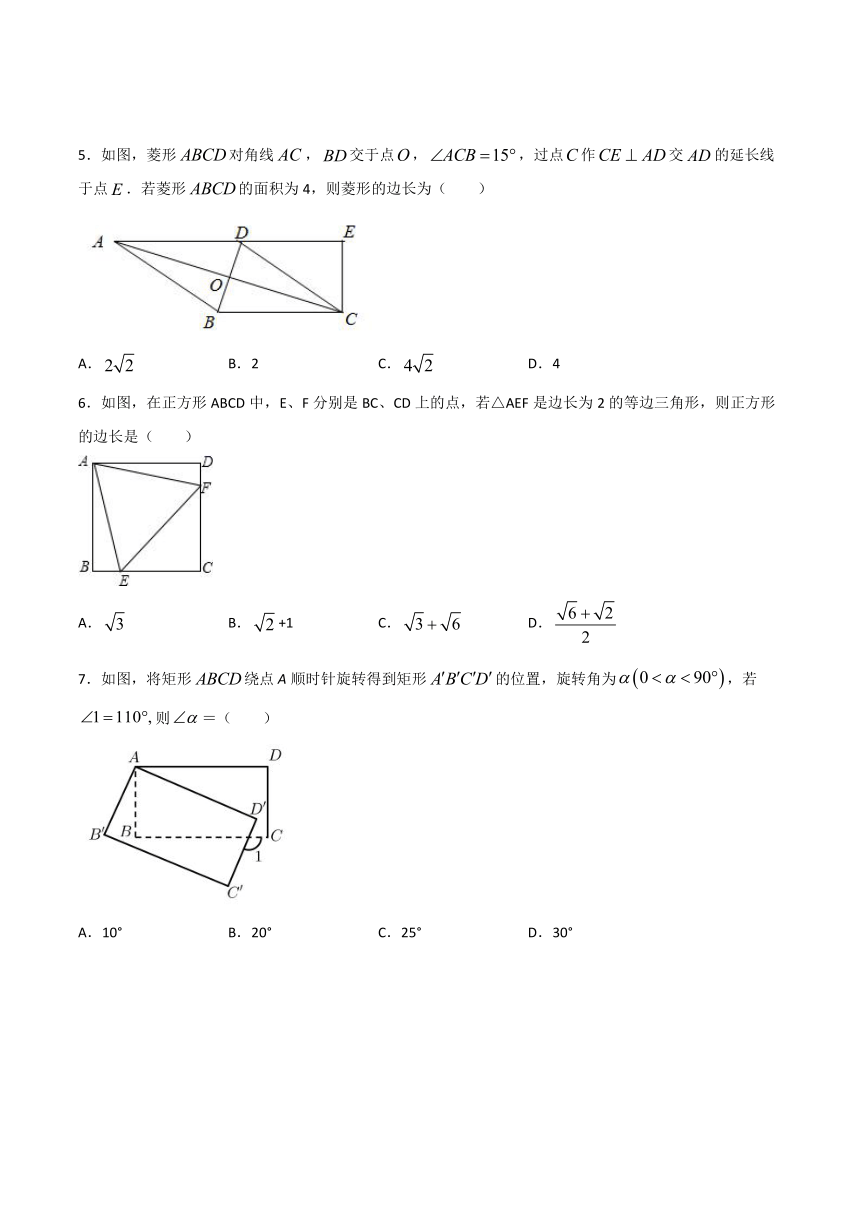
2.如图,点E在菱形ABCD的AB边上,点F在BC边的延长线上,连接CE,DF,对于下列条件:①BE=CF;②CE⊥AB,DF⊥BC;③CE=DF;④∠BCE=∠CDF,只选其中一个添加,不能确定△BCE≌△CDF的是(
)
A.①
B.②
C.③
D.④
3.如图,在矩形ABCD中,AB=5,AD=12,对角线BD的垂直平分线分别与AD,BC边交于点E、F,则四边形BFDE的面积为( )
A.
B.
C.
D.
4.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,恰好使的D落在边BC上的点F处,如果∠BAF=60°,则∠DAE的大小为(
)
A.10°
B.15
°
C.20
°
D.25°
5.如图,菱形对角线,交于点,,过点作交的延长线于点.若菱形的面积为4,则菱形的边长为(
)
A.
B.2
C.
D.4
6.如图,在正方形ABCD中,E、F分别是BC、CD上的点,若△AEF是边长为2的等边三角形,则正方形的边长是( )
A.
B.+1
C.
D.
7.如图,将矩形绕点A顺时针旋转得到矩形的位置,旋转角为,若则=(
)
A.10°
B.20°
C.25°
D.30°
8.如图,将矩形纸片沿其对角线折叠,使点落到点的位置,与交于点,若,,则图中阴影部分的周长为(
)
A.10
B.13
C.17
D.20
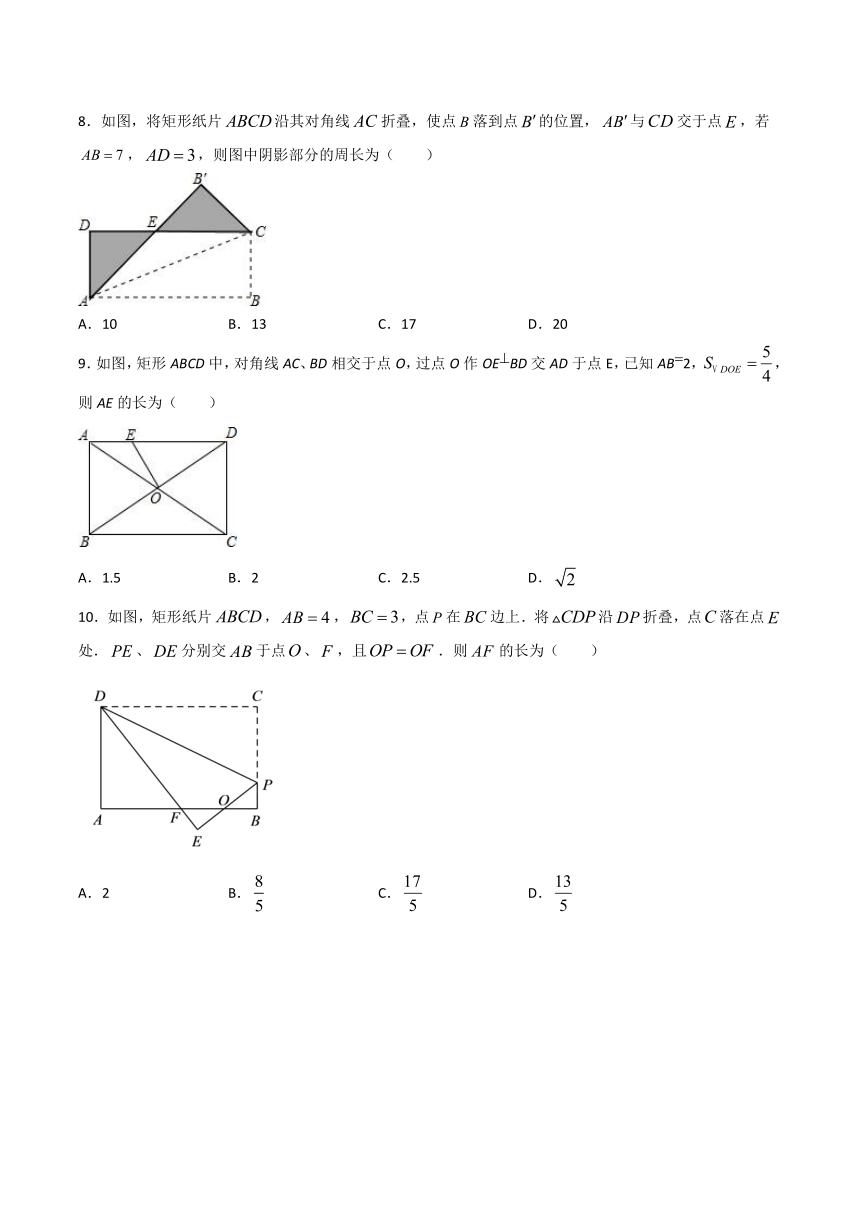
9.如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OEBD交AD于点E,已知AB2,,则AE的长为(
)
A.1.5
B.2
C.2.5
D.
10.如图,矩形纸片,,,点在边上.将沿折叠,点落在点处.、分别交于点、,且.则的长为(
)
A.2
B.
C.
D.
11.如图,在矩形ABCD中,在CD上取点E,连接AE,在AE,AB上分别取点F,G,连接DF,GF,,将沿FD翻折,点A落在BC边的处,若,且,,的长是(
)
A.
B.
C.
D.
12.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点(P不与B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是(
)
A.≤AM<6
B.≤AM<12
C.≤AM<12
D.≤AM<6
二、填空题
13.若菱形的一个内角为60°,周长为16,则其面积为_____.
14.如图,菱形ABCD的边长为4,∠A=45°,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M、N两点,直线MN交AD于点E,连接CE,则CE的长为____________.
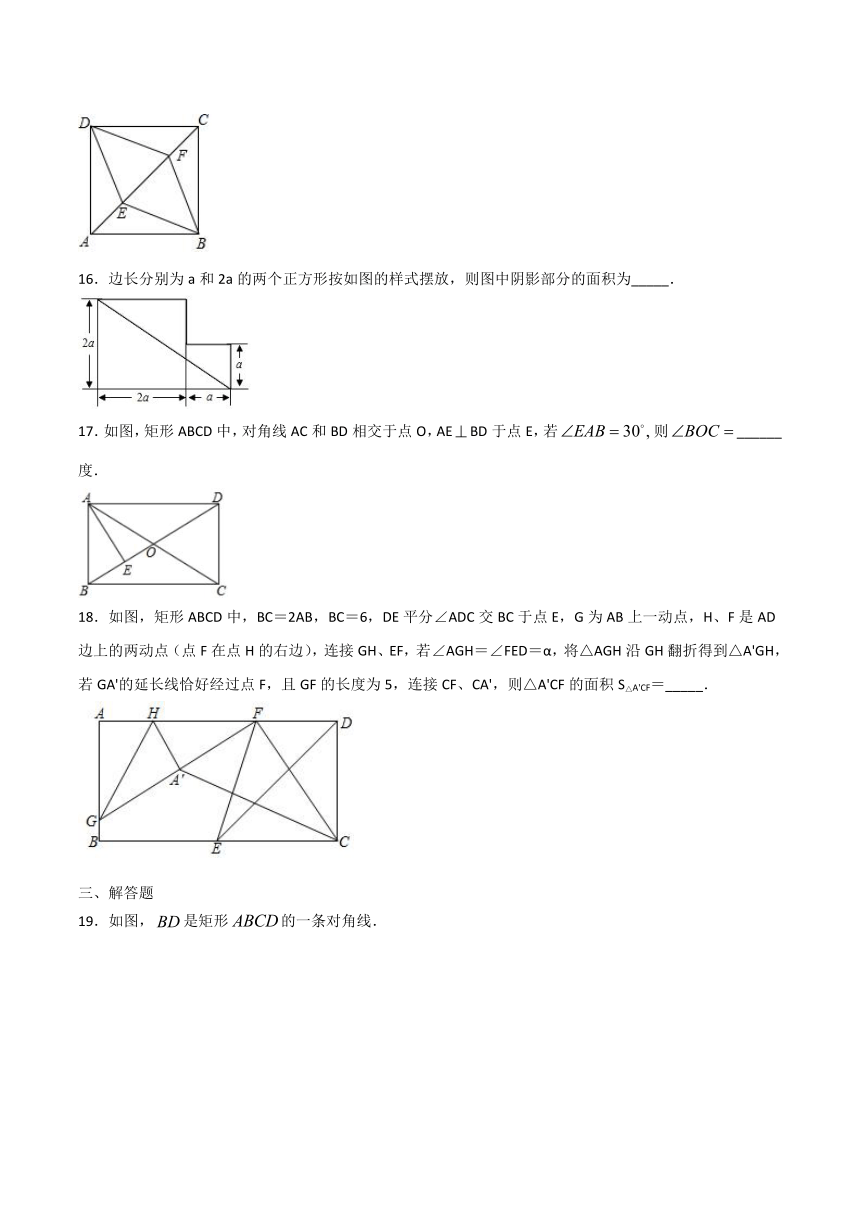
15.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是_____.
16.边长分别为a和2a的两个正方形按如图的样式摆放,则图中阴影部分的面积为_____.
17.如图,矩形ABCD中,对角线AC和BD相交于点O,AEBD于点E,若则______度.
18.如图,矩形ABCD中,BC=2AB,BC=6,DE平分∠ADC交BC于点E,G为AB上一动点,H、F是AD边上的两动点(点F在点H的右边),连接GH、EF,若∠AGH=∠FED=α,将△AGH沿GH翻折得到△A'GH,若GA'的延长线恰好经过点F,且GF的长度为5,连接CF、CA',则△A'CF的面积S△A'CF=_____.
三、解答题
19.如图,是矩形的一条对角线.
(1)作的垂直平分线,分别交,于点、.垂足为点(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)求证:.
20.如图,四边形是正方形,为上一点,连接,延长至点,使得,过点作,垂足为,求证:.
21.如图所示,在菱形ABCD中,E、F分别为AB、AD上两点,AE=AF.
(1)求证:CE=CF;
(2)若∠ECF=60°,∠B=80°,试问BC=CE吗?请说明理由.
22.如图,已知菱形的对角线,交于点,分别过点,作,的垂线,两垂线交于点.
(1)请判断四边形的形状并给出证明;
(2)若四边形的面积为12,点是四边形对角线的中点,且,请计算四边形的周长.
23.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
(2)将图①中BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)将图①中BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).
24.如图,在菱形中,分别过点作的垂线,过点作的垂线交于点.
(1)如图1,若,连接,求证:;
(2)如图2,若,点是延长线上的一点,点为延长线上的一点,且.连接,交的延长线于点,连接.试猜想线段的数量关系并证明你的结论;
(3)如图3,在(2)的条件下,在上取一点,使得,已知为直线上一点,连接,连接,当最小时,直接写出的值.
参考答案
1.D
解:顺次连接一个四边形的各边中点,得到的四边形是平行四边形,
若四边形的对角线互相垂直,则所得平行四边形为矩形,则满足条件的是②④,
2.C
解:∵四边形ABCD是菱形,
∴BC=CD,AB//CD,
∴∠B=∠DCF,
①添加BE=CF,
在△BCE和△CDF中
,
∴△BCE≌△CDF(SAS),
②添加CE⊥AB,DF⊥BC,
则∠CEB=∠F=90°,
在△BCE和△CDF中
,
∴△BCE≌△CDF(AAS),
③∵添加CE=DF,
不能确定△BCE≌△CDF;
④添加∠BCE=∠CDF,
在△BCE和△CDF中
,
∴△BCE≌△CDF(ASA),
故选:C.
3.A
解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,∠EDO=∠FBO,
∵对角线BD的垂直平分线分别与AD,BC边交于点E、F,
∴BO=DO,EF⊥BD,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∵BO=DO,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形,
∴BE=DE,
∵AB=5,AD=12,∠A=90°,
∴BD=13,
设DE=x,则AE=12﹣x,
在Rt△AEB中,AB2+AE2=BE2,
即52+(12﹣x)2=x2,
∴x,
∴BE=DE,
在Rt△BEO中,OE,
∴EF=2EO,
∴菱形BEDF的面积,
4.B
∵四边形ABCD为矩形,
∴,
∵是由沿AE折叠而来,且F点恰好落在BC上,
∴,
∵,
∴.
5.A
解:∵四边形ABCD是菱形,
∴AD=CD,AD∥BC,
∴∠EDC=∠BCD=2∠ACB=30°,
∵CE⊥AD,
∴∠CED=90°,
∴CE=DC=AD,
∴菱形ABCD的面积=AD?CE=AD?AD=AD2=4,
∴AD=(负值舍去),
即菱形的边长为,
6.D
由题知:△AEF是边长为2的等边三角形,
∴∠EAF=60°,AE=AF,∴∠BAE+∠DAF=30°,
又AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF(HL),
∴∠BAE=∠DAF=15°,
如图,作∠AEH=∠BAE=15°,交AB于H,
∴∠BHE=30°,AH=HE,∴HE=2BE=AH,BH=BE,∴AB=(2+)BE,
∵AE2=BE2+AB2,
∴4=BE2+(2+)2×BE2,
∴BE=(﹣1)=,
∴AB=(2+)BE=,
7.B
如图所示:
根据旋转的性质知:∠D′=∠D=90°,∠DAD′=α,
∵,
∴.
∴.
∵∠DAD′=α,
∴.
8.D
解:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°,
∵∠B′EC=∠DEA,
在△AED和△CEB′中,
,
∴△AED≌△CEB′(AAS);
∴EA=EC,
∴阴影部分的周长为AD+DE+EA+EB′+B′C+EC
=AD+DE+EC+EA+EB′+B′C
=AD+DC+AB′+B′C
=3+7+7+3
=20,
故选:D.
9.A
解:连接BE,如图所示:
由题意可得,OE为对角线BD的垂直平分线,
∴BE=DE,S△BOE=S△DOE=,
∴S△BDE=2S△BOE=,
∴DE?AB=,
又∵AB=2,
∴DE=,
∴BE=,
在Rt△ABE中,由勾股定理得:AE==1.5,
故选:A.
10.B
∵四边形ABCD是矩形
∴,,
根据折叠的性质,得:,,
在与中
∴
∴,
∴
设,则
∴
∴
在中,由勾股定理得:
解得:
即
故选:B
11.A
解:连接
由折叠得,∠
∵
∴∠
∵
∴∠
∵∠
∴∠
∴△是等腰直角三角形,
∴
∵∠
∴
∴
∴
∴
故选:A.
12.A
解:在Rt△ABC中,∵∠BAC=90°,AB=5,AC=12,
∴BC=,
∵PE⊥AB于E,PF⊥AC于F,
∴∠PEA=∠PFA=∠EAF=90°,
∴四边形AEPF是矩形,
∵M是EF的中点,
∴延长AM经过点P,
∴EF=AP,AM=EF=PA,
当PA⊥CB时,PA=,
∴AM的最小值为,
∵PA<AC,
∴PA<12,
∴AM<6,
∴≤AM<6,
故选:A.
13.
解:如图,∵菱形的周长为16,
∴边长AB=BC=16÷4=4,
∵一个内角∠B=60°,
∴△ABC是等边三角形,
过点A作AE⊥BC于点E,
则,
根据勾股定理,,
所以,菱形的面积为4×2=.
故答案为:.
14.2
解:连接BE,如图:
由题意可知,MN垂直平分AB,
∴AE=BE,
∴
∠AEB=90°,
在等腰直角三角形ABE中,AB=4,
由
∴
∵四边形ABCD为菱形,
∴,
∴∠EBC=∠AEB=90°,
在Rt△BCE中,由勾股定理得:
15.8.
解:如图,连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC,
∵AE=CF=2,
∴OA-AE=OC-CF,即OE=OF,
∴四边形BEDF为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,
∴DE=DF=BE=BF,
∵AC=BD=8,OE=OF==2,
由勾股定理得:,
∴四边形BEDF的周长=4DE=4×2=8,
故答案为:8.
16.2a2
解:阴影部分的面积=大正方形的面积+小正方形的面积﹣直角三角形的面积
=(2a)2+a2﹣?2a?3a
=4a2+a2﹣3a2
=2a2.
故答案为:2a2.
17.120
解:∵四边形是矩形
∴
∵AEBD,
∴,
∴是等边三角形,
∴
∴
故答案为:120.
18.
解:在矩形ABCD中,ED平分∠ADC
∴∠EDC=45°
∵∠DCE=90°
∴∠DEC=45°
∴△ECD是等腰直角三角形
∴EC=DC
∵BC=2AB=2DC
∴E为BC中点
∴
∵△翻折到△
∴△
∴∠
∴
∵∠
∠
∴△
∴△△△全等,
∴∠
∴
∴
∴
∴∠
∴∠,
∴
∴
.
19.
(1)解:如图所示:即为所求;
(2)证明:连接BE,
四边形为矩形,
,
.
垂直平分线段,
,
.
在和中,,
,
,
又,
BD垂直平分EF,
.
20.
证明:四边形为正方形,
,,
,
,
,
在和中,,
,
.
21.
(1)证明:∵ABCD是菱形,
∴AB=AD,BC=CD,∠B=∠D,
∵AE=AF,
∴AB﹣AE=AD﹣AF,
∴BE=DF,
在△BCE与△DCF中,∵,
∴△BCE≌△DCF,
∴CE=CF;
(2)结论是:BC=CE.
理由如下:
∵ABCD是菱形,∠B=80°,
∴∠A=100°,
∵AE=AF,
∴
由(1)知CE=CF,∠ECF=60°,
∴△CEF是等边三角形,
∴∠CEF=60°,
∴∠CEB=180°﹣60°﹣40°=80°,
∴∠B=∠CEB,
∴BC=CE.
22.
解:(1)四边形是矩形.
理由如下:
∵四边形是菱形,
∴,
∴.
∵,,
∴,
∴四边形是矩形.
(2)由(1)知,四边形是矩形,
∴.
∵点是矩形对角线的中点,
∴,
∴.
∵四边形的面积为12,
∴.
在中,由勾股定理,得,
∴,
∴,
即四边形的周长为14.
23.
(1)证明:∵四边形ABCD是正方形,
∴∠DCF=90°,
在Rt△FCD中,
∵G为DF的中点,
∴CG=FD,
同理,在Rt△DEF中,
EG=FD,
∴CG=EG.
(2)解:(1)中结论仍然成立,即EG=CG.
证法:如图,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点,
在△DAG与△DCG中,
∵AD=CD,∠ADG=∠CDG,DG=DG,
∴△DAG≌△DCG(SAS),
∴AG=CG;
在△DMG与△FNG中,
∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴△DMG≌△FNG(ASA),
∴MG=NG;
∵∠EAM=∠AEN=∠AMN=90°,
∴四边形AENM是矩形,
在矩形AENM中,AM=EN,
在△AMG与△ENG中,
∵AM=EN,∠AMG=∠ENG,MG=NG,
∴△AMG≌△ENG(SAS),
∴AG=EG,
∴EG=CG.
(3)解:(1)中的结论仍然成立.理由如下:
如图,过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N,
∵G为FD中点,
∴FG=GD,
∵MF∥CD,
∴∠FMG=∠DCG,∠GDC=∠GFM,
∴△CDG≌△MFG,
∴CD=FM,
∵NF∥BC,
∴∠NFH+∠NHF=∠EHB+∠EBH,
又∵∠NHF=∠EBH,
∴∠NFH=∠EBH,
∴∠EFM=∠EBC,
又∵BE=EF,
则△EFM≌△EBC,∠FEM=∠BEC,EM=EC
∵∠FEC+∠BEC=90°,
∴∠FEC+∠FEM=90°,即∠MEC=90°,
∴△MEC是等腰直角三角形,
∵G为CM中点,
∴EG=CG,EG⊥CG.
24
(1)如图,延长BA交DE于点M.
∵四边形ABCD为菱形,,
∴,
∵,
∴.
∴,.
∵
∴,
∴,
∴.
在和中,,
∴.
∴.
(2)如图,连接BD,取BF上一点N,使BN=DH,连接AN,EC,作于点O.
在和中,
∴,
∴,
由题意可知,
∵,
∴,
∴,
∴为等边三角形.
∴,
∴,,即.
在和中,,
∴.
∴,
∵,
∴,即,
在和中,,
∴.
∴,,
∵,
∴,
∴,
∴,,
∴,
∴,
∴.
(3)取P关于DE的对称点,连接交DE于点Q,此时BQ+PQ最小,即为,
∵,
∴,
,
又∵,2AP=HP
∴点Q为BA延长线上的点,
∴,
∴,
∴.
试卷第1页,总3页
9.4矩形
菱形
正方形同步基础培优训练题
一、单选题
1.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是(
)
①平行四边形;②菱形;③任意四边形;④对角线互相垂直的四边形
A.①③
B.②③
C.③④
D.②④
2.如图,点E在菱形ABCD的AB边上,点F在BC边的延长线上,连接CE,DF,对于下列条件:①BE=CF;②CE⊥AB,DF⊥BC;③CE=DF;④∠BCE=∠CDF,只选其中一个添加,不能确定△BCE≌△CDF的是(
)
A.①
B.②
C.③
D.④
3.如图,在矩形ABCD中,AB=5,AD=12,对角线BD的垂直平分线分别与AD,BC边交于点E、F,则四边形BFDE的面积为( )
A.
B.
C.
D.
4.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,恰好使的D落在边BC上的点F处,如果∠BAF=60°,则∠DAE的大小为(
)
A.10°
B.15
°
C.20
°
D.25°
5.如图,菱形对角线,交于点,,过点作交的延长线于点.若菱形的面积为4,则菱形的边长为(
)
A.
B.2
C.
D.4
6.如图,在正方形ABCD中,E、F分别是BC、CD上的点,若△AEF是边长为2的等边三角形,则正方形的边长是( )
A.
B.+1
C.
D.
7.如图,将矩形绕点A顺时针旋转得到矩形的位置,旋转角为,若则=(
)
A.10°
B.20°
C.25°
D.30°
8.如图,将矩形纸片沿其对角线折叠,使点落到点的位置,与交于点,若,,则图中阴影部分的周长为(
)
A.10
B.13
C.17
D.20
9.如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OEBD交AD于点E,已知AB2,,则AE的长为(
)
A.1.5
B.2
C.2.5
D.
10.如图,矩形纸片,,,点在边上.将沿折叠,点落在点处.、分别交于点、,且.则的长为(
)
A.2
B.
C.
D.
11.如图,在矩形ABCD中,在CD上取点E,连接AE,在AE,AB上分别取点F,G,连接DF,GF,,将沿FD翻折,点A落在BC边的处,若,且,,的长是(
)
A.
B.
C.
D.
12.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点(P不与B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是(
)
A.≤AM<6
B.≤AM<12
C.≤AM<12
D.≤AM<6
二、填空题
13.若菱形的一个内角为60°,周长为16,则其面积为_____.
14.如图,菱形ABCD的边长为4,∠A=45°,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M、N两点,直线MN交AD于点E,连接CE,则CE的长为____________.
15.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是_____.
16.边长分别为a和2a的两个正方形按如图的样式摆放,则图中阴影部分的面积为_____.
17.如图,矩形ABCD中,对角线AC和BD相交于点O,AEBD于点E,若则______度.
18.如图,矩形ABCD中,BC=2AB,BC=6,DE平分∠ADC交BC于点E,G为AB上一动点,H、F是AD边上的两动点(点F在点H的右边),连接GH、EF,若∠AGH=∠FED=α,将△AGH沿GH翻折得到△A'GH,若GA'的延长线恰好经过点F,且GF的长度为5,连接CF、CA',则△A'CF的面积S△A'CF=_____.
三、解答题
19.如图,是矩形的一条对角线.
(1)作的垂直平分线,分别交,于点、.垂足为点(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)求证:.
20.如图,四边形是正方形,为上一点,连接,延长至点,使得,过点作,垂足为,求证:.
21.如图所示,在菱形ABCD中,E、F分别为AB、AD上两点,AE=AF.
(1)求证:CE=CF;
(2)若∠ECF=60°,∠B=80°,试问BC=CE吗?请说明理由.
22.如图,已知菱形的对角线,交于点,分别过点,作,的垂线,两垂线交于点.
(1)请判断四边形的形状并给出证明;
(2)若四边形的面积为12,点是四边形对角线的中点,且,请计算四边形的周长.
23.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
(2)将图①中BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)将图①中BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).
24.如图,在菱形中,分别过点作的垂线,过点作的垂线交于点.
(1)如图1,若,连接,求证:;
(2)如图2,若,点是延长线上的一点,点为延长线上的一点,且.连接,交的延长线于点,连接.试猜想线段的数量关系并证明你的结论;
(3)如图3,在(2)的条件下,在上取一点,使得,已知为直线上一点,连接,连接,当最小时,直接写出的值.
参考答案
1.D
解:顺次连接一个四边形的各边中点,得到的四边形是平行四边形,
若四边形的对角线互相垂直,则所得平行四边形为矩形,则满足条件的是②④,
2.C
解:∵四边形ABCD是菱形,
∴BC=CD,AB//CD,
∴∠B=∠DCF,
①添加BE=CF,
在△BCE和△CDF中
,
∴△BCE≌△CDF(SAS),
②添加CE⊥AB,DF⊥BC,
则∠CEB=∠F=90°,
在△BCE和△CDF中
,
∴△BCE≌△CDF(AAS),
③∵添加CE=DF,
不能确定△BCE≌△CDF;
④添加∠BCE=∠CDF,
在△BCE和△CDF中
,
∴△BCE≌△CDF(ASA),
故选:C.
3.A
解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,∠EDO=∠FBO,
∵对角线BD的垂直平分线分别与AD,BC边交于点E、F,
∴BO=DO,EF⊥BD,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∵BO=DO,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形,
∴BE=DE,
∵AB=5,AD=12,∠A=90°,
∴BD=13,
设DE=x,则AE=12﹣x,
在Rt△AEB中,AB2+AE2=BE2,
即52+(12﹣x)2=x2,
∴x,
∴BE=DE,
在Rt△BEO中,OE,
∴EF=2EO,
∴菱形BEDF的面积,
4.B
∵四边形ABCD为矩形,
∴,
∵是由沿AE折叠而来,且F点恰好落在BC上,
∴,
∵,
∴.
5.A
解:∵四边形ABCD是菱形,
∴AD=CD,AD∥BC,
∴∠EDC=∠BCD=2∠ACB=30°,
∵CE⊥AD,
∴∠CED=90°,
∴CE=DC=AD,
∴菱形ABCD的面积=AD?CE=AD?AD=AD2=4,
∴AD=(负值舍去),
即菱形的边长为,
6.D
由题知:△AEF是边长为2的等边三角形,
∴∠EAF=60°,AE=AF,∴∠BAE+∠DAF=30°,
又AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF(HL),
∴∠BAE=∠DAF=15°,
如图,作∠AEH=∠BAE=15°,交AB于H,
∴∠BHE=30°,AH=HE,∴HE=2BE=AH,BH=BE,∴AB=(2+)BE,
∵AE2=BE2+AB2,
∴4=BE2+(2+)2×BE2,
∴BE=(﹣1)=,
∴AB=(2+)BE=,
7.B
如图所示:
根据旋转的性质知:∠D′=∠D=90°,∠DAD′=α,
∵,
∴.
∴.
∵∠DAD′=α,
∴.
8.D
解:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°,
∵∠B′EC=∠DEA,
在△AED和△CEB′中,
,
∴△AED≌△CEB′(AAS);
∴EA=EC,
∴阴影部分的周长为AD+DE+EA+EB′+B′C+EC
=AD+DE+EC+EA+EB′+B′C
=AD+DC+AB′+B′C
=3+7+7+3
=20,
故选:D.
9.A
解:连接BE,如图所示:
由题意可得,OE为对角线BD的垂直平分线,
∴BE=DE,S△BOE=S△DOE=,
∴S△BDE=2S△BOE=,
∴DE?AB=,
又∵AB=2,
∴DE=,
∴BE=,
在Rt△ABE中,由勾股定理得:AE==1.5,
故选:A.
10.B
∵四边形ABCD是矩形
∴,,
根据折叠的性质,得:,,
在与中
∴
∴,
∴
设,则
∴
∴
在中,由勾股定理得:
解得:
即
故选:B
11.A
解:连接
由折叠得,∠
∵
∴∠
∵
∴∠
∵∠
∴∠
∴△是等腰直角三角形,
∴
∵∠
∴
∴
∴
∴
故选:A.
12.A
解:在Rt△ABC中,∵∠BAC=90°,AB=5,AC=12,
∴BC=,
∵PE⊥AB于E,PF⊥AC于F,
∴∠PEA=∠PFA=∠EAF=90°,
∴四边形AEPF是矩形,
∵M是EF的中点,
∴延长AM经过点P,
∴EF=AP,AM=EF=PA,
当PA⊥CB时,PA=,
∴AM的最小值为,
∵PA<AC,
∴PA<12,
∴AM<6,
∴≤AM<6,
故选:A.
13.
解:如图,∵菱形的周长为16,
∴边长AB=BC=16÷4=4,
∵一个内角∠B=60°,
∴△ABC是等边三角形,
过点A作AE⊥BC于点E,
则,
根据勾股定理,,
所以,菱形的面积为4×2=.
故答案为:.
14.2
解:连接BE,如图:
由题意可知,MN垂直平分AB,
∴AE=BE,
∴
∠AEB=90°,
在等腰直角三角形ABE中,AB=4,
由
∴
∵四边形ABCD为菱形,
∴,
∴∠EBC=∠AEB=90°,
在Rt△BCE中,由勾股定理得:
15.8.
解:如图,连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC,
∵AE=CF=2,
∴OA-AE=OC-CF,即OE=OF,
∴四边形BEDF为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,
∴DE=DF=BE=BF,
∵AC=BD=8,OE=OF==2,
由勾股定理得:,
∴四边形BEDF的周长=4DE=4×2=8,
故答案为:8.
16.2a2
解:阴影部分的面积=大正方形的面积+小正方形的面积﹣直角三角形的面积
=(2a)2+a2﹣?2a?3a
=4a2+a2﹣3a2
=2a2.
故答案为:2a2.
17.120
解:∵四边形是矩形
∴
∵AEBD,
∴,
∴是等边三角形,
∴
∴
故答案为:120.
18.
解:在矩形ABCD中,ED平分∠ADC
∴∠EDC=45°
∵∠DCE=90°
∴∠DEC=45°
∴△ECD是等腰直角三角形
∴EC=DC
∵BC=2AB=2DC
∴E为BC中点
∴
∵△翻折到△
∴△
∴∠
∴
∵∠
∠
∴△
∴△△△全等,
∴∠
∴
∴
∴
∴∠
∴∠,
∴
∴
.
19.
(1)解:如图所示:即为所求;
(2)证明:连接BE,
四边形为矩形,
,
.
垂直平分线段,
,
.
在和中,,
,
,
又,
BD垂直平分EF,
.
20.
证明:四边形为正方形,
,,
,
,
,
在和中,,
,
.
21.
(1)证明:∵ABCD是菱形,
∴AB=AD,BC=CD,∠B=∠D,
∵AE=AF,
∴AB﹣AE=AD﹣AF,
∴BE=DF,
在△BCE与△DCF中,∵,
∴△BCE≌△DCF,
∴CE=CF;
(2)结论是:BC=CE.
理由如下:
∵ABCD是菱形,∠B=80°,
∴∠A=100°,
∵AE=AF,
∴
由(1)知CE=CF,∠ECF=60°,
∴△CEF是等边三角形,
∴∠CEF=60°,
∴∠CEB=180°﹣60°﹣40°=80°,
∴∠B=∠CEB,
∴BC=CE.
22.
解:(1)四边形是矩形.
理由如下:
∵四边形是菱形,
∴,
∴.
∵,,
∴,
∴四边形是矩形.
(2)由(1)知,四边形是矩形,
∴.
∵点是矩形对角线的中点,
∴,
∴.
∵四边形的面积为12,
∴.
在中,由勾股定理,得,
∴,
∴,
即四边形的周长为14.
23.
(1)证明:∵四边形ABCD是正方形,
∴∠DCF=90°,
在Rt△FCD中,
∵G为DF的中点,
∴CG=FD,
同理,在Rt△DEF中,
EG=FD,
∴CG=EG.
(2)解:(1)中结论仍然成立,即EG=CG.
证法:如图,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点,
在△DAG与△DCG中,
∵AD=CD,∠ADG=∠CDG,DG=DG,
∴△DAG≌△DCG(SAS),
∴AG=CG;
在△DMG与△FNG中,
∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴△DMG≌△FNG(ASA),
∴MG=NG;
∵∠EAM=∠AEN=∠AMN=90°,
∴四边形AENM是矩形,
在矩形AENM中,AM=EN,
在△AMG与△ENG中,
∵AM=EN,∠AMG=∠ENG,MG=NG,
∴△AMG≌△ENG(SAS),
∴AG=EG,
∴EG=CG.
(3)解:(1)中的结论仍然成立.理由如下:
如图,过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N,
∵G为FD中点,
∴FG=GD,
∵MF∥CD,
∴∠FMG=∠DCG,∠GDC=∠GFM,
∴△CDG≌△MFG,
∴CD=FM,
∵NF∥BC,
∴∠NFH+∠NHF=∠EHB+∠EBH,
又∵∠NHF=∠EBH,
∴∠NFH=∠EBH,
∴∠EFM=∠EBC,
又∵BE=EF,
则△EFM≌△EBC,∠FEM=∠BEC,EM=EC
∵∠FEC+∠BEC=90°,
∴∠FEC+∠FEM=90°,即∠MEC=90°,
∴△MEC是等腰直角三角形,
∵G为CM中点,
∴EG=CG,EG⊥CG.
24
(1)如图,延长BA交DE于点M.
∵四边形ABCD为菱形,,
∴,
∵,
∴.
∴,.
∵
∴,
∴,
∴.
在和中,,
∴.
∴.
(2)如图,连接BD,取BF上一点N,使BN=DH,连接AN,EC,作于点O.
在和中,
∴,
∴,
由题意可知,
∵,
∴,
∴,
∴为等边三角形.
∴,
∴,,即.
在和中,,
∴.
∴,
∵,
∴,即,
在和中,,
∴.
∴,,
∵,
∴,
∴,
∴,,
∴,
∴,
∴.
(3)取P关于DE的对称点,连接交DE于点Q,此时BQ+PQ最小,即为,
∵,
∴,
,
又∵,2AP=HP
∴点Q为BA延长线上的点,
∴,
∴,
∴.
试卷第1页,总3页
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
