2020-2021学年八年级数学下册人教版习题课件 18.2 特殊的平行四边形18.2.1 矩形第2课时 矩形的判定(共23张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学下册人教版习题课件 18.2 特殊的平行四边形18.2.1 矩形第2课时 矩形的判定(共23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 511.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第十八章 平行四边形
人教版
18.2 特殊的平行四边形
18.2.1 矩形
第2课时 矩形的判定
知识点1:有一个角是直角的平行四边形是矩形
1.如图是用四根木棒搭成的平行四边形框架,AB=8
cm,AD=6
cm,使AB固定,转动AD,当∠DAB=________时,四边形ABCD是矩形.
90°
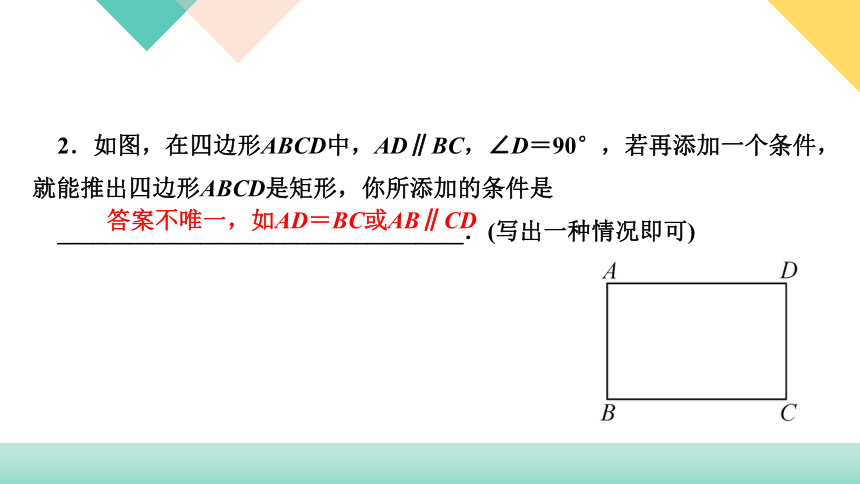
2.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是
__________________________________.(写出一种情况即可)
答案不唯一,如AD=BC或AB∥CD
3.如图,在?ABCD中,E,F为BC上两点,且BE=CF,AF=DE.求证:四边形ABCD是矩形.
证明:∵BE=CF,∴BF=CE.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,在△ABF和△DCE中,∵BF=CE,AF=DE,AB=CD,∴△ABF≌△DCE,∴∠B=∠C.∵AB∥CD,∴∠B+∠C=180°,∴∠B=∠C=90°,∴四边形ABCD是矩形
知识点2:对角线相等的平行四边形是矩形
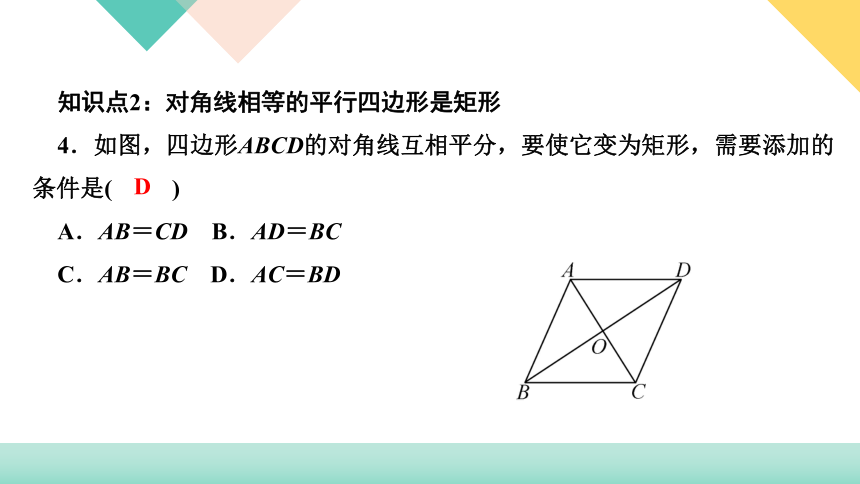
4.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是(
)
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
D
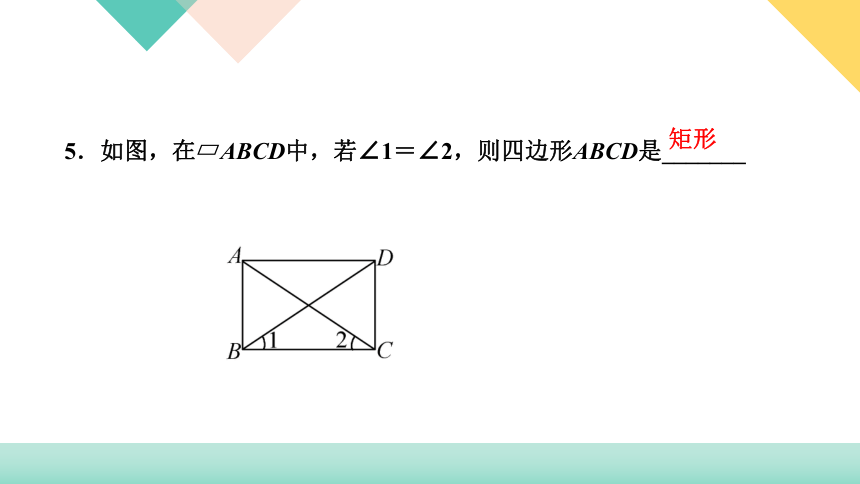
5.如图,在?ABCD中,若∠1=∠2,则四边形ABCD是_______
矩形
6.(2020·聊城)如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠BAE=∠CFE,∠ABE=∠FCE,∵E为BC的中点,∴EB=EC,∴△ABE≌△FCE(AAS),∴AB=CF.
∵AB∥CF,∴四边形ABFC是平行四边形,∵BC=AD,AD=AF,∴BC=AF,∴四边形ABFC是矩形
知识点3:有三个角是直角的四边形是矩形
7.已知O为四边形ABCD对角线的交点,下列条件能使四边形ABCD成为矩形的是(
)
A.OA=OC,OB=OD
B.AC=BD
C.AC⊥BD
D.∠ABC=∠BCD=∠CDA=90°
D
8.(怀化中考)已知:如图,在?ABCD中,AE⊥BC,CF⊥AD,E,F分别为垂足.
(1)求证:△ABE≌△CDF;
(2)求证:四边形AECF是矩形.
A
10.如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFGH为矩形,则四边形ABCD一定满足(
)
A.AB=CD
B.AC=BD
C.AC⊥BD
D.AD∥BC
C
11.在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,2),要使四边形OBCA为矩形,则C点的坐标为___________.
(3,2)
12.如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,当AB,BC满足条件___________时,四边形PEMF为矩形.
BC=2AB
13.(2020·遂宁)如图,在△ABC中,AB=AC,点D,E分别是线段BC,AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
证明:(1)∵AF∥BC,∴∠AFE=∠DBE,∵E是线段AD的中点,∴AE=DE,∵∠AEF=∠DEB,∴△BDE≌△FAE(AAS)
(2)∵△BDE≌△FAE,∴AF=BD,∵D是线段BC的中点,∴BD=CD,∴AF=CD,∵AF∥CD,∴四边形ADCF是平行四边形,∵AB=AC,∴AD⊥BC,∴∠ADC=90°,∴四边形ADCF为矩形
14.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
15.(青岛中考)如图,在?ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
(2)当AC=2AB时,四边形EGCF是矩形;理由如下:∵AC=2OA,AC=2AB,∴AB=OA,∵E是OB的中点,∴AG⊥OB,∴∠OEG=90°,同理:CF⊥OD,∴AG∥CF,∴EG∥CF,∵EG=AE,OA=OC,∴OE是△ACG的中位线,∴OE∥CG,∴EF∥CG,∴四边形EGCF是平行四边形,∵∠OEG=90°,∴四边形EGCF是矩形
第十八章 平行四边形
人教版
18.2 特殊的平行四边形
18.2.1 矩形
第2课时 矩形的判定
知识点1:有一个角是直角的平行四边形是矩形
1.如图是用四根木棒搭成的平行四边形框架,AB=8
cm,AD=6
cm,使AB固定,转动AD,当∠DAB=________时,四边形ABCD是矩形.
90°
2.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是
__________________________________.(写出一种情况即可)
答案不唯一,如AD=BC或AB∥CD
3.如图,在?ABCD中,E,F为BC上两点,且BE=CF,AF=DE.求证:四边形ABCD是矩形.
证明:∵BE=CF,∴BF=CE.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,在△ABF和△DCE中,∵BF=CE,AF=DE,AB=CD,∴△ABF≌△DCE,∴∠B=∠C.∵AB∥CD,∴∠B+∠C=180°,∴∠B=∠C=90°,∴四边形ABCD是矩形
知识点2:对角线相等的平行四边形是矩形
4.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是(
)
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
D
5.如图,在?ABCD中,若∠1=∠2,则四边形ABCD是_______
矩形
6.(2020·聊城)如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠BAE=∠CFE,∠ABE=∠FCE,∵E为BC的中点,∴EB=EC,∴△ABE≌△FCE(AAS),∴AB=CF.
∵AB∥CF,∴四边形ABFC是平行四边形,∵BC=AD,AD=AF,∴BC=AF,∴四边形ABFC是矩形
知识点3:有三个角是直角的四边形是矩形
7.已知O为四边形ABCD对角线的交点,下列条件能使四边形ABCD成为矩形的是(
)
A.OA=OC,OB=OD
B.AC=BD
C.AC⊥BD
D.∠ABC=∠BCD=∠CDA=90°
D
8.(怀化中考)已知:如图,在?ABCD中,AE⊥BC,CF⊥AD,E,F分别为垂足.
(1)求证:△ABE≌△CDF;
(2)求证:四边形AECF是矩形.
A
10.如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFGH为矩形,则四边形ABCD一定满足(
)
A.AB=CD
B.AC=BD
C.AC⊥BD
D.AD∥BC
C
11.在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,2),要使四边形OBCA为矩形,则C点的坐标为___________.
(3,2)
12.如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,当AB,BC满足条件___________时,四边形PEMF为矩形.
BC=2AB
13.(2020·遂宁)如图,在△ABC中,AB=AC,点D,E分别是线段BC,AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
证明:(1)∵AF∥BC,∴∠AFE=∠DBE,∵E是线段AD的中点,∴AE=DE,∵∠AEF=∠DEB,∴△BDE≌△FAE(AAS)
(2)∵△BDE≌△FAE,∴AF=BD,∵D是线段BC的中点,∴BD=CD,∴AF=CD,∵AF∥CD,∴四边形ADCF是平行四边形,∵AB=AC,∴AD⊥BC,∴∠ADC=90°,∴四边形ADCF为矩形
14.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
15.(青岛中考)如图,在?ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
(2)当AC=2AB时,四边形EGCF是矩形;理由如下:∵AC=2OA,AC=2AB,∴AB=OA,∵E是OB的中点,∴AG⊥OB,∴∠OEG=90°,同理:CF⊥OD,∴AG∥CF,∴EG∥CF,∵EG=AE,OA=OC,∴OE是△ACG的中位线,∴OE∥CG,∴EF∥CG,∴四边形EGCF是平行四边形,∵∠OEG=90°,∴四边形EGCF是矩形
