2020—2021学年北师大版数学八年级下册教学课件-4.3 第2课时 利用完全平方公式进行因式分解(共17张ppt)
文档属性
| 名称 | 2020—2021学年北师大版数学八年级下册教学课件-4.3 第2课时 利用完全平方公式进行因式分解(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 16:20:58 | ||
图片预览






文档简介
(共17张PPT)
第四章
因式分解
3
第2课时
利用完全平方公式进行因式分解
课堂小结
例题讲解
获取新知
随堂演练
知识回顾
知识回顾
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式逆用
a2-b2=(a+b)(a-b)
今天我们学习用公式因式分解的另一个公式:完全平方公式
获取新知
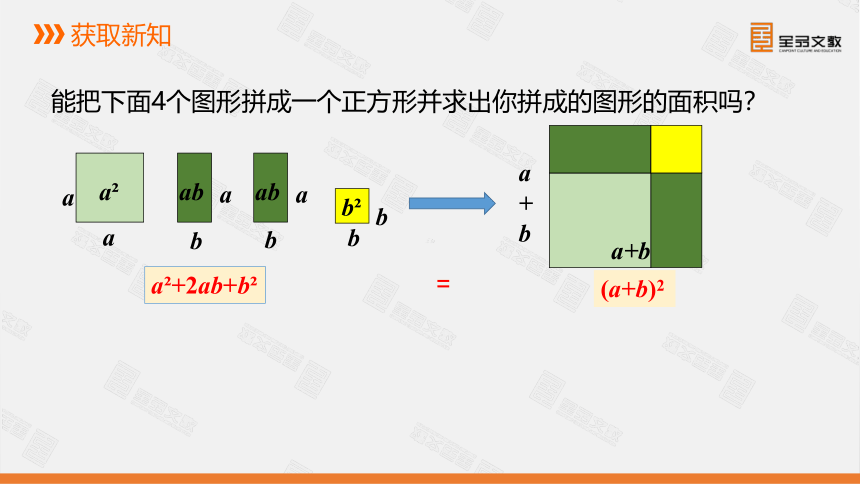
能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
a
a
b
b
a
b
a
b
ab
a?
b?
ab
a+b
a+b
a?+2ab+b?
=
(a+b)2
简记口诀:首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a
±
b)?
a2
首2
+尾2
±2×首×尾
(首±尾)2
例题讲解
例1
把下列完全平方式因式分解:
(1)x2+14x+49;
(2)
(m+n)2
-6
(m+n)+9.
解:(1)x2+14x+49
=
x2+2×7x+72
=
(x+7)
2
;
a2
+
2
a
b
+
b2
=
(a+b)2
(2)(m+n)2-6(m+n)+9
=(m+n)2-2·(m+n)·32+32=(m+n-3)2.
a2
-
+
b2
=
(a-b)2
2
a
b
备注:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成完全平方的形式,就能用完全平方公式因式分解.
例2
把下列各式因式分解:
(1)3ax2+6axy+3ay2;(2)-x2-4y2+4xy.
解:(1)3ax2+6axy+3ay2
=
3a(x2+2xy+y2)=3a(x+y)2;
a2
+
2ab
+
b2
=
(a+b)2
方法总结:分解因式前应先分析多项式的特点,
一般先提公因式,再套用公式,平方项为负的先提出负号.
注意分解因式必须进行到每一个多项式都不能再分解因式为止.
(2)-x2-4y2+4xy=
-(x2+4y2-4xy)
=
-(x2-4xy+4y2)=-[x2-2·x·2y+(2y)2]=
-(x-2y)2.
a2
-
+
b2
=
(a-b)2
2
a
b
随堂演练
1.
下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1
B.x2+2x-1
C.x2-1
D.x2-6x+9
D
2.
已知x2+16x+k是完全平方式,则常数k等于( )
A.64
B.48
C.32
D.16
A
3.
把多项式(a+b)2-4(a2-b2)+4(a-b)2因式分解的结果为( )
A.(3a-b)2
B.(3b+a)2
C.(3b-a)2
D.(3a+b)2
C
4.对照
a?±2ab+b?=(a±b)?,填空:
③.a?+4ab+4b?=(
)?+2·
(
)
·(
)+(
)?=(
)?
②.m?-6m+9=(
)?
-
2·
(
)
·(
)+(
)?
=(
)?
①.
x?+4x+4=
(
)?
+2·(
)·(
)+(
)?
=(
)?
x
2
x
+
2
a
a
2b
a
+
2b
2b
m
m
-
3
3
x
2
m
3
5.
若代数式x2+kx+25是一个完全平方式,则k=____.
±10
6.
若一个长方形的面积是x3+2x2+x(x>0),且一边长为x+1,则其邻边长为________.
x2+x
7.
分解因式:
(1)x2-12x+36;
(2)-x2+4xy-4y2;
(3)4(2a+b)2-4(2a+b)+1;(4)y2+2y+1-x2
解:(1)原式
=x2-2·x·6+(6)2
=(x-6)2;
(2)原式
==-(x2-4xy+4y2)
=-(x-2y)2;
(3)原式=[2(2a+b)]?
-
2·2(2a+b)·1+(1)?
=(4a+2b
-
1)2;
(4)原式=(y+1)?
-x?
=(y+1+x)(y+1-x).
8.简便运算:
(1)1002-2×100×99+99?;(2)342+34×32+162.
解:(1)原式=(100-99)?=1
(2)原式=(34+16)2=2500
课堂小结
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负
完全平方公式分解因式
《练就优等生》:
4.3
第2课时
第四章
因式分解
3
第2课时
利用完全平方公式进行因式分解
课堂小结
例题讲解
获取新知
随堂演练
知识回顾
知识回顾
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式逆用
a2-b2=(a+b)(a-b)
今天我们学习用公式因式分解的另一个公式:完全平方公式
获取新知
能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
a
a
b
b
a
b
a
b
ab
a?
b?
ab
a+b
a+b
a?+2ab+b?
=
(a+b)2
简记口诀:首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a
±
b)?
a2
首2
+尾2
±2×首×尾
(首±尾)2
例题讲解
例1
把下列完全平方式因式分解:
(1)x2+14x+49;
(2)
(m+n)2
-6
(m+n)+9.
解:(1)x2+14x+49
=
x2+2×7x+72
=
(x+7)
2
;
a2
+
2
a
b
+
b2
=
(a+b)2
(2)(m+n)2-6(m+n)+9
=(m+n)2-2·(m+n)·32+32=(m+n-3)2.
a2
-
+
b2
=
(a-b)2
2
a
b
备注:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成完全平方的形式,就能用完全平方公式因式分解.
例2
把下列各式因式分解:
(1)3ax2+6axy+3ay2;(2)-x2-4y2+4xy.
解:(1)3ax2+6axy+3ay2
=
3a(x2+2xy+y2)=3a(x+y)2;
a2
+
2ab
+
b2
=
(a+b)2
方法总结:分解因式前应先分析多项式的特点,
一般先提公因式,再套用公式,平方项为负的先提出负号.
注意分解因式必须进行到每一个多项式都不能再分解因式为止.
(2)-x2-4y2+4xy=
-(x2+4y2-4xy)
=
-(x2-4xy+4y2)=-[x2-2·x·2y+(2y)2]=
-(x-2y)2.
a2
-
+
b2
=
(a-b)2
2
a
b
随堂演练
1.
下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1
B.x2+2x-1
C.x2-1
D.x2-6x+9
D
2.
已知x2+16x+k是完全平方式,则常数k等于( )
A.64
B.48
C.32
D.16
A
3.
把多项式(a+b)2-4(a2-b2)+4(a-b)2因式分解的结果为( )
A.(3a-b)2
B.(3b+a)2
C.(3b-a)2
D.(3a+b)2
C
4.对照
a?±2ab+b?=(a±b)?,填空:
③.a?+4ab+4b?=(
)?+2·
(
)
·(
)+(
)?=(
)?
②.m?-6m+9=(
)?
-
2·
(
)
·(
)+(
)?
=(
)?
①.
x?+4x+4=
(
)?
+2·(
)·(
)+(
)?
=(
)?
x
2
x
+
2
a
a
2b
a
+
2b
2b
m
m
-
3
3
x
2
m
3
5.
若代数式x2+kx+25是一个完全平方式,则k=____.
±10
6.
若一个长方形的面积是x3+2x2+x(x>0),且一边长为x+1,则其邻边长为________.
x2+x
7.
分解因式:
(1)x2-12x+36;
(2)-x2+4xy-4y2;
(3)4(2a+b)2-4(2a+b)+1;(4)y2+2y+1-x2
解:(1)原式
=x2-2·x·6+(6)2
=(x-6)2;
(2)原式
==-(x2-4xy+4y2)
=-(x-2y)2;
(3)原式=[2(2a+b)]?
-
2·2(2a+b)·1+(1)?
=(4a+2b
-
1)2;
(4)原式=(y+1)?
-x?
=(y+1+x)(y+1-x).
8.简便运算:
(1)1002-2×100×99+99?;(2)342+34×32+162.
解:(1)原式=(100-99)?=1
(2)原式=(34+16)2=2500
课堂小结
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负
完全平方公式分解因式
《练就优等生》:
4.3
第2课时
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
