2020-2021学年北师大版数学七年级下册2.1.1对顶角、余角和补角课件(共29张ppt)
文档属性
| 名称 | 2020-2021学年北师大版数学七年级下册2.1.1对顶角、余角和补角课件(共29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 16:27:26 | ||
图片预览



文档简介
(共29张PPT)
2.1
余角与补角
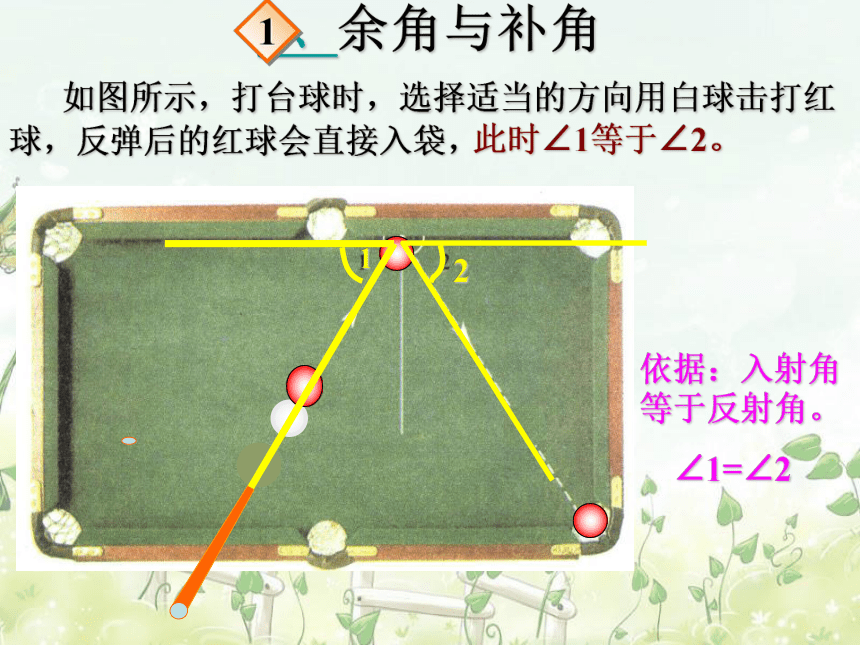
如图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,
1、余角与补角
1
此时∠1等于∠2。
1
2
依据:入射角等于反射角。
∠1=∠2
余角
与
补角
的定义
1
2
图
2–1
C
A
B
D
E
F
∠2
∠1
=
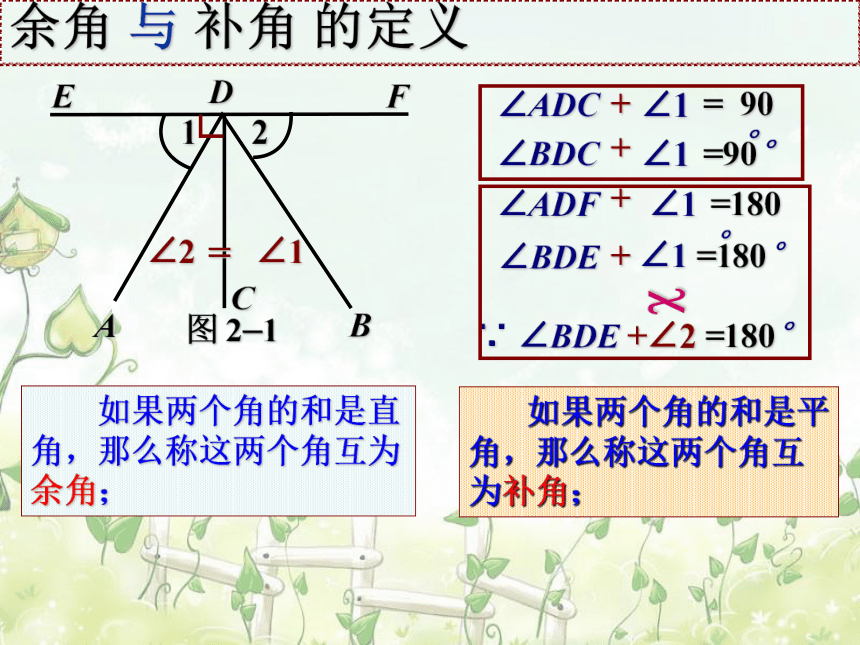
∠ADC
∠1
+
=
90°
∠BDC
∠1
+
=90°
∠ADF
∠1
+
=180°
+
∠1
=180°
∠BDE
∵
∠BDE
+∠2
=180°
?
如果两个角的和是直角,那么称这两个角互为余角;
如果两个角的和是平角,那么称这两个角互为补角;
余角
与
补角
的判断
1
2
图
2–1
C
A
B
D
E
F
∠2
∠1
=
想一想
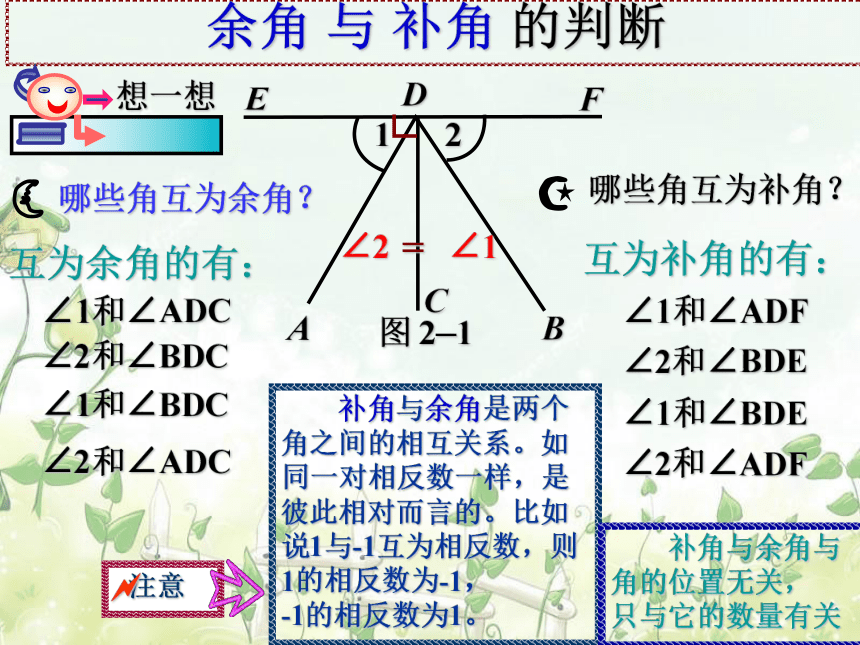
哪些角互为余角?
哪些角互为补角?
∠1和∠ADC
∠1和∠BDC
互为余角的有:
∠2和∠ADC
∠2和∠BDC
∠1和∠ADF
∠1和∠BDE
互为补角的有:
∠2和∠ADF
∠2和∠BDE
补角与余角是两个角之间的相互关系。如同一对相反数一样,是彼此相对而言的。比如说1与-1互为相反数,则1的相反数为-1,
-1的相反数为1。
注意
?
补角与余角与角的位置无关,
只与它的数量有关
(90°-X)
(180°-X)
30°
120°
①一个角为60°,则它的余角为_______
;
②一个锐角为X,则它的余角为_______;
③一个角为60°,则它的补角为_______;
④一个角为X,则它的补角为_______;
如图(1)∠1与∠2是一对什么角?(其中∠3是直角)
如图(2)∠1与∠2是一对什么角?
如图(3)∠1与∠2是一对什么角?
∠3与∠4呢?(其中∠3、∠4是直角)
1
3
2
(1)
1
2
(2)
3
1
2
4
(3)
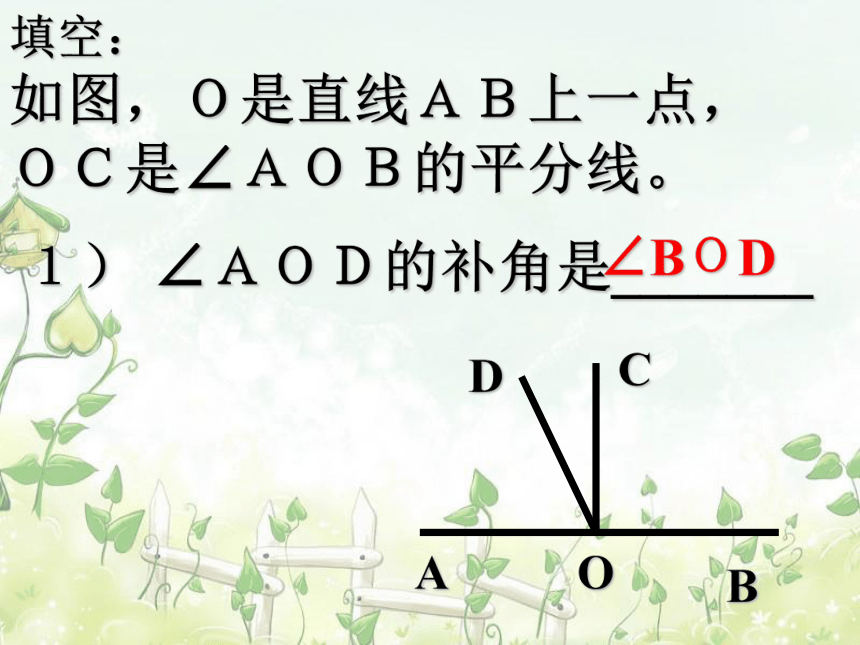
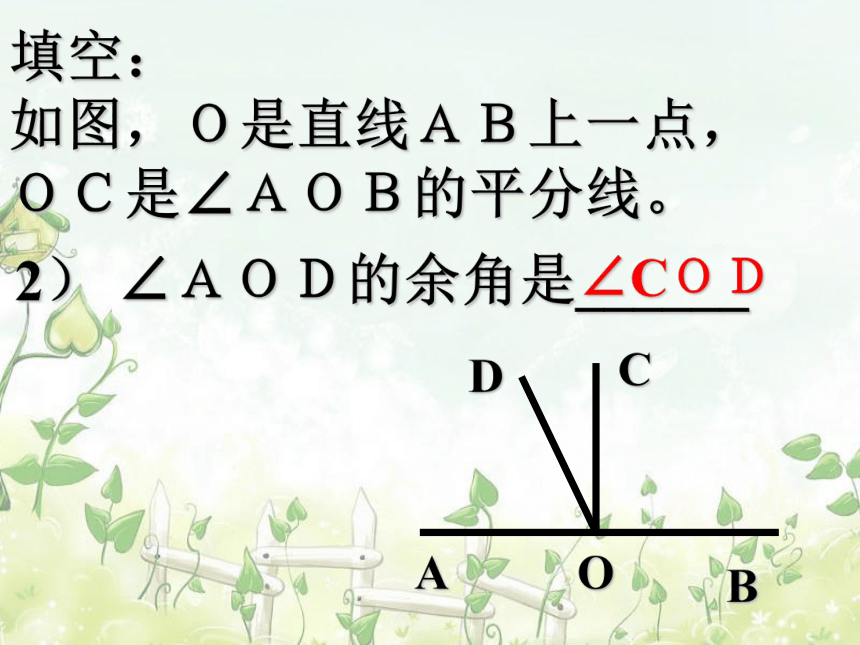
填空:
如图,O是直线AB上一点,
OC是∠AOB的平分线。
1)
∠AOD的补角是_______
A
O
B
D
C
∠BOD
A
O
B
D
C
填空:
如图,O是直线AB上一点,OC是∠AOB的平分线。
2)
∠AOD的余角是______
∠COD
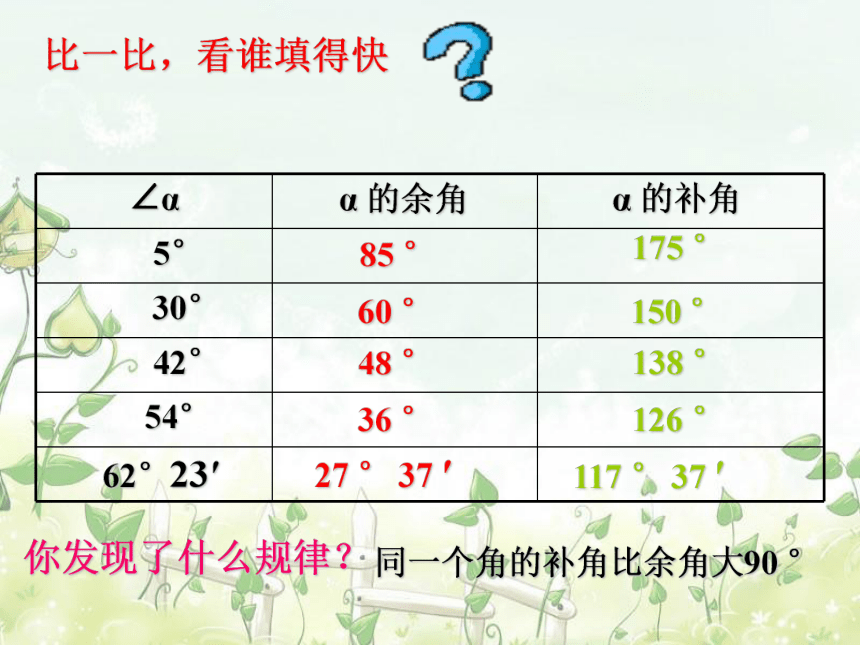
∠α
α
的余角
α
的补角
5°
30°
42°
54°
62°23′
比一比,看谁填得快
85
°
175
°
60
°
150
°
48
°
138
°
36
°
126
°
27
°
37
′
117
°
37
′
你发现了什么规律?
同一个角的补角比余角大90
°
想一想
1、已知,
ON⊥DE
,?1=
?2,试回答以下几个问题:
(1)哪些角互为余角?哪些角互为补角?
(2)
?3与?4有什么关系?为什么?
(3)
?AOE与?BOD有什么关系?为什么?
同角或等角的余角相等,同角或等角的补角相等
E
O
N
A
B
D
1
2
3
4
∠1
=∠2
,
?
由此我们可得:
余角
与
补角
的
性
质
1
2
E
F
D
C
5
4
3
1=
2,
CD
EF
已知
且
2+
5=90。
1=58。,
2、
5与
1有什么关系?
5等于多少度?
1、
3、
5与
3有什么关系?你的依据是什么?
例.
一个角的补角是这个角的2倍,求这个角的度数.
解法一
解法二
解:
设这个角的度数
x,
则它的补角的度数为
根据题意得:
即
答:这个角为60°.
180-x
180-x=2x
180=2x+x
3x=180
X=60
解:
设这个角的度数x,
则它的补角的度数为
根据题意得:
60
=
x
答:这个角为60°.
2、
一个角比它的余角小20°,它的补角是多少度?
1、一个角是它补角的3倍,这个角是多少度?
思考题:
解:
设这个角的度数为x度,
由题意得:
设这个角的度数为x度
请你试一试
1、已知:一个锐角的补角加上20°后等于这
角的3倍。
求:这个角的度数
2、已知:一个锐角的补角加上20°后等于这个角余
角的3倍。
求:这个角的度数
比一比
:
看谁快
1.
如图A、O、
B在同一直线上,
∠AOC=
∠DOE=
C
A
O
B
D
E
)
)
(
)
4
3
1
2
若∠1=2∠4,求∠2的度数
解:设∠4
=x,则∠1=2x
∵∠1+∠DOE+∠4=1800
∴∠2=∠3
(同角的余角相等)
∴∠2=
30
°
即∠4=30°
解得x=30°
∴2x+90°+x=180°
又∵∠2+∠COE=90°
∠4+∠COE=90°
用代数方法解决几何问题是常用的一种策略。
互余的角
互补的角
数量关系
对应图形
性质
C
D
E
N
A
O
B
M
?1+
?2=90°
?1+
?2=180°
同角(等角)的余角相等
同角(等角)的补角相等
小结
对顶角
(1)用剪刀剪东西时,哪对角同时变大或变小?
图2-2
(2)如果将图2-2简单地表示为
图2-3,
议一议
那么∠1与∠2的位置有什么关系?
∠1
=∠2
。
能试着说明你的理由吗?
∠2与∠3互补,
∠1与∠3互补,
3
∴
∠1
=∠2。
它们的大小有什么关系?
2
1
A
B
C
D
图2-3
O
及其性质
直线AB与CD相交于点O,
对顶角相等
∠1与∠2有公共顶点,
它们的两边互为反向延长线,
引入概念:如图2-3,
这样的两个角叫做对顶角。
略动脑筋
35°
35°
如图,这两个角是对顶角吗?
下列图形中,∠1和∠2是对顶角的图形是
(
)
1
1
1
1
2
2
2
2
(A)
(B)
(C)
(D)
C
注意:(1)一个角的对顶角只有一个,
(2)掌握对顶角的概念要注意三点:
1°是两条直线相交而得;2°有一个公共顶点;3°没有公共边,三个条件缺一不可。
知识梳理
◣
◢
巩固
如果两个角的和是直角,那么称这两个角互为
;
的两个角称作互为补角;
余角
和是平角
的位置
只与它的
有关。
数量
同角或等角
同角或等角
2组
有公共顶点,两边互为反向延长线的两个角叫做
。
两直线相交所成的四个角中,
有
对顶角.
对顶角
补角与余角是两个角之间的相互关系。
补角和余角与角
无关,
的余角相等,
的补角相等;
对顶角
。
相等
如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角是多少度吗?你的根据是什么?
答:40°
方法一:可利用对顶角相等得出。
议
一
议
方法二:可利用补角得出。
用对顶角相等解题
你能用量角器量出图中∠1的度数吗?
原来是:
只要量出它的对顶角就可以了!
脑筋急转弯!
池塘
1
2
∠1
=∠2
。
(1)若∠β与∠α是对顶角
,
∠α=20°,则∠β=______
20°.
35°
145°
(2)如图直线AB与CD相交于O点,
OA平分∠EOC,
∠EOC=70°,则∠BOD=_____,
∠BOC=______.
A
B
C
D
O
E
练一练
练习
1、如图,在长方形的台球桌面上,∠1+∠3=90°
∠
2=
∠3。如果∠
2=
58°,那么∠1等于多少度?
试着与同伴交流你的理由。
答:32°
理由:∠1=90°-∠3
=
90°-∠2
=
90°-58
°
=32
°
2、当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象(如图所示)。图中与是对顶角吗?
答:∠1和∠2
不是对顶角。因为:∠2的一条边不是∠1的反向延长线。
游戏:折一折
算一算
1、
如图1,把三角形的一角折叠得到折痕EF,
已知:∠EFB=
,求:
∠EFC的度数
(
(
F
E
D
C
B
A
如图1
F
C
A
(
B
D
E
(
G
如图2
2、如图2所示折叠,已知∠EFG=75°,
求:
∠BFE的度数
小结
归纳:本节课学习了什么内容、方法、
应注意什么问题?
所学概念?1.互为余角;
2.互为补角;
3.对顶角。
所学性质?1.同角或等角的余角相等;
2.同角或等角的补角相等;
3.对顶角相等。
收获很多还要会整理!
2.1
余角与补角
如图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,
1、余角与补角
1
此时∠1等于∠2。
1
2
依据:入射角等于反射角。
∠1=∠2
余角
与
补角
的定义
1
2
图
2–1
C
A
B
D
E
F
∠2
∠1
=
∠ADC
∠1
+
=
90°
∠BDC
∠1
+
=90°
∠ADF
∠1
+
=180°
+
∠1
=180°
∠BDE
∵
∠BDE
+∠2
=180°
?
如果两个角的和是直角,那么称这两个角互为余角;
如果两个角的和是平角,那么称这两个角互为补角;
余角
与
补角
的判断
1
2
图
2–1
C
A
B
D
E
F
∠2
∠1
=
想一想
哪些角互为余角?
哪些角互为补角?
∠1和∠ADC
∠1和∠BDC
互为余角的有:
∠2和∠ADC
∠2和∠BDC
∠1和∠ADF
∠1和∠BDE
互为补角的有:
∠2和∠ADF
∠2和∠BDE
补角与余角是两个角之间的相互关系。如同一对相反数一样,是彼此相对而言的。比如说1与-1互为相反数,则1的相反数为-1,
-1的相反数为1。
注意
?
补角与余角与角的位置无关,
只与它的数量有关
(90°-X)
(180°-X)
30°
120°
①一个角为60°,则它的余角为_______
;
②一个锐角为X,则它的余角为_______;
③一个角为60°,则它的补角为_______;
④一个角为X,则它的补角为_______;
如图(1)∠1与∠2是一对什么角?(其中∠3是直角)
如图(2)∠1与∠2是一对什么角?
如图(3)∠1与∠2是一对什么角?
∠3与∠4呢?(其中∠3、∠4是直角)
1
3
2
(1)
1
2
(2)
3
1
2
4
(3)
填空:
如图,O是直线AB上一点,
OC是∠AOB的平分线。
1)
∠AOD的补角是_______
A
O
B
D
C
∠BOD
A
O
B
D
C
填空:
如图,O是直线AB上一点,OC是∠AOB的平分线。
2)
∠AOD的余角是______
∠COD
∠α
α
的余角
α
的补角
5°
30°
42°
54°
62°23′
比一比,看谁填得快
85
°
175
°
60
°
150
°
48
°
138
°
36
°
126
°
27
°
37
′
117
°
37
′
你发现了什么规律?
同一个角的补角比余角大90
°
想一想
1、已知,
ON⊥DE
,?1=
?2,试回答以下几个问题:
(1)哪些角互为余角?哪些角互为补角?
(2)
?3与?4有什么关系?为什么?
(3)
?AOE与?BOD有什么关系?为什么?
同角或等角的余角相等,同角或等角的补角相等
E
O
N
A
B
D
1
2
3
4
∠1
=∠2
,
?
由此我们可得:
余角
与
补角
的
性
质
1
2
E
F
D
C
5
4
3
1=
2,
CD
EF
已知
且
2+
5=90。
1=58。,
2、
5与
1有什么关系?
5等于多少度?
1、
3、
5与
3有什么关系?你的依据是什么?
例.
一个角的补角是这个角的2倍,求这个角的度数.
解法一
解法二
解:
设这个角的度数
x,
则它的补角的度数为
根据题意得:
即
答:这个角为60°.
180-x
180-x=2x
180=2x+x
3x=180
X=60
解:
设这个角的度数x,
则它的补角的度数为
根据题意得:
60
=
x
答:这个角为60°.
2、
一个角比它的余角小20°,它的补角是多少度?
1、一个角是它补角的3倍,这个角是多少度?
思考题:
解:
设这个角的度数为x度,
由题意得:
设这个角的度数为x度
请你试一试
1、已知:一个锐角的补角加上20°后等于这
角的3倍。
求:这个角的度数
2、已知:一个锐角的补角加上20°后等于这个角余
角的3倍。
求:这个角的度数
比一比
:
看谁快
1.
如图A、O、
B在同一直线上,
∠AOC=
∠DOE=
C
A
O
B
D
E
)
)
(
)
4
3
1
2
若∠1=2∠4,求∠2的度数
解:设∠4
=x,则∠1=2x
∵∠1+∠DOE+∠4=1800
∴∠2=∠3
(同角的余角相等)
∴∠2=
30
°
即∠4=30°
解得x=30°
∴2x+90°+x=180°
又∵∠2+∠COE=90°
∠4+∠COE=90°
用代数方法解决几何问题是常用的一种策略。
互余的角
互补的角
数量关系
对应图形
性质
C
D
E
N
A
O
B
M
?1+
?2=90°
?1+
?2=180°
同角(等角)的余角相等
同角(等角)的补角相等
小结
对顶角
(1)用剪刀剪东西时,哪对角同时变大或变小?
图2-2
(2)如果将图2-2简单地表示为
图2-3,
议一议
那么∠1与∠2的位置有什么关系?
∠1
=∠2
。
能试着说明你的理由吗?
∠2与∠3互补,
∠1与∠3互补,
3
∴
∠1
=∠2。
它们的大小有什么关系?
2
1
A
B
C
D
图2-3
O
及其性质
直线AB与CD相交于点O,
对顶角相等
∠1与∠2有公共顶点,
它们的两边互为反向延长线,
引入概念:如图2-3,
这样的两个角叫做对顶角。
略动脑筋
35°
35°
如图,这两个角是对顶角吗?
下列图形中,∠1和∠2是对顶角的图形是
(
)
1
1
1
1
2
2
2
2
(A)
(B)
(C)
(D)
C
注意:(1)一个角的对顶角只有一个,
(2)掌握对顶角的概念要注意三点:
1°是两条直线相交而得;2°有一个公共顶点;3°没有公共边,三个条件缺一不可。
知识梳理
◣
◢
巩固
如果两个角的和是直角,那么称这两个角互为
;
的两个角称作互为补角;
余角
和是平角
的位置
只与它的
有关。
数量
同角或等角
同角或等角
2组
有公共顶点,两边互为反向延长线的两个角叫做
。
两直线相交所成的四个角中,
有
对顶角.
对顶角
补角与余角是两个角之间的相互关系。
补角和余角与角
无关,
的余角相等,
的补角相等;
对顶角
。
相等
如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角是多少度吗?你的根据是什么?
答:40°
方法一:可利用对顶角相等得出。
议
一
议
方法二:可利用补角得出。
用对顶角相等解题
你能用量角器量出图中∠1的度数吗?
原来是:
只要量出它的对顶角就可以了!
脑筋急转弯!
池塘
1
2
∠1
=∠2
。
(1)若∠β与∠α是对顶角
,
∠α=20°,则∠β=______
20°.
35°
145°
(2)如图直线AB与CD相交于O点,
OA平分∠EOC,
∠EOC=70°,则∠BOD=_____,
∠BOC=______.
A
B
C
D
O
E
练一练
练习
1、如图,在长方形的台球桌面上,∠1+∠3=90°
∠
2=
∠3。如果∠
2=
58°,那么∠1等于多少度?
试着与同伴交流你的理由。
答:32°
理由:∠1=90°-∠3
=
90°-∠2
=
90°-58
°
=32
°
2、当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象(如图所示)。图中与是对顶角吗?
答:∠1和∠2
不是对顶角。因为:∠2的一条边不是∠1的反向延长线。
游戏:折一折
算一算
1、
如图1,把三角形的一角折叠得到折痕EF,
已知:∠EFB=
,求:
∠EFC的度数
(
(
F
E
D
C
B
A
如图1
F
C
A
(
B
D
E
(
G
如图2
2、如图2所示折叠,已知∠EFG=75°,
求:
∠BFE的度数
小结
归纳:本节课学习了什么内容、方法、
应注意什么问题?
所学概念?1.互为余角;
2.互为补角;
3.对顶角。
所学性质?1.同角或等角的余角相等;
2.同角或等角的补角相等;
3.对顶角相等。
收获很多还要会整理!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
