2020-2021学年七年级数学北师大版下册 4.1.2 三角形的三边关系 课件(共53张PPT)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册 4.1.2 三角形的三边关系 课件(共53张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 16:32:36 | ||
图片预览





文档简介
(共53张PPT)
第四章
认识三角形
4.1.2
三角形的三边关系
北师大版数学七年级下册
1.掌握和理解三角形的三边关系。
2.认识三角形的稳定性,并能利用三角形的稳定性解决一些实际问题。
学习目标
1.三角形的定义是什么?三角形按角分为哪几类?
2.三角形的内角和是多少度?直角三角形两锐角有何关系?
复习导入
1
知识点
等腰三角形
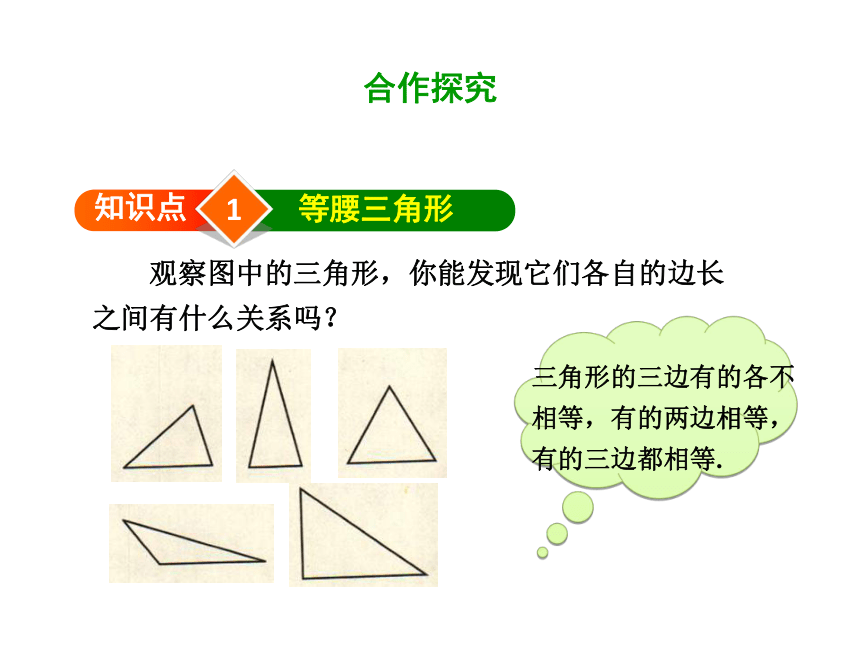
观察图中的三角形,你能发现它们各自的边长
之间有什么关系吗?
三角形的三边有的各不相等,有的两边相等,有的三边都相等.
合作探究
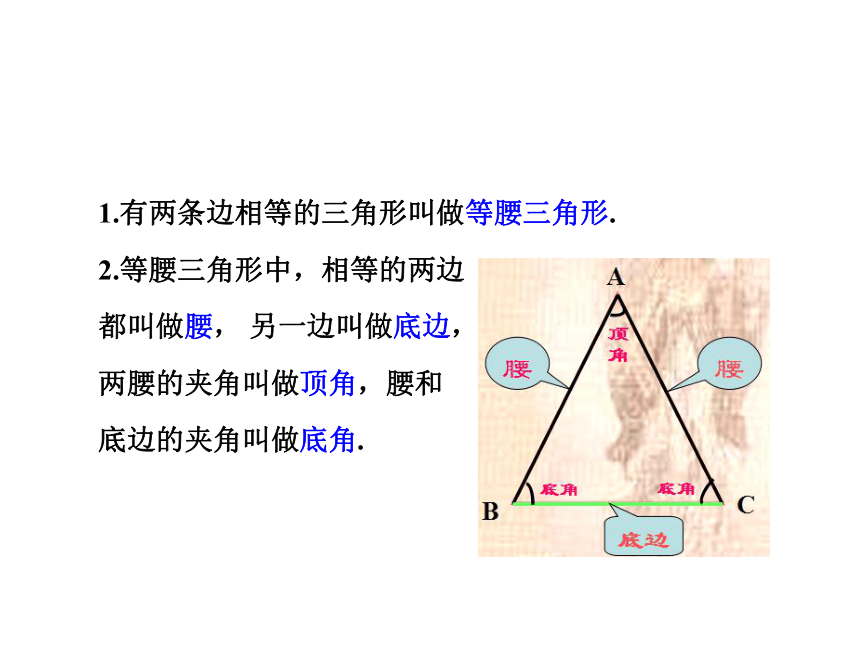
1.有两条边相等的三角形叫做等腰三角形.
2.等腰三角形中,相等的两边
都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,腰和
底边的夹角叫做底角.
例1
1.等腰三角形一腰为3cm,底为4cm,则它的周长是__________;
2.等腰三角形的一边长为3cm,另一边长为4cm,则
它的周长是______________;
3.等腰三角形的一边长为3cm,另一边长为8cm,则
它的周长是__________.
10cm
10cm或11cm
19cm
1
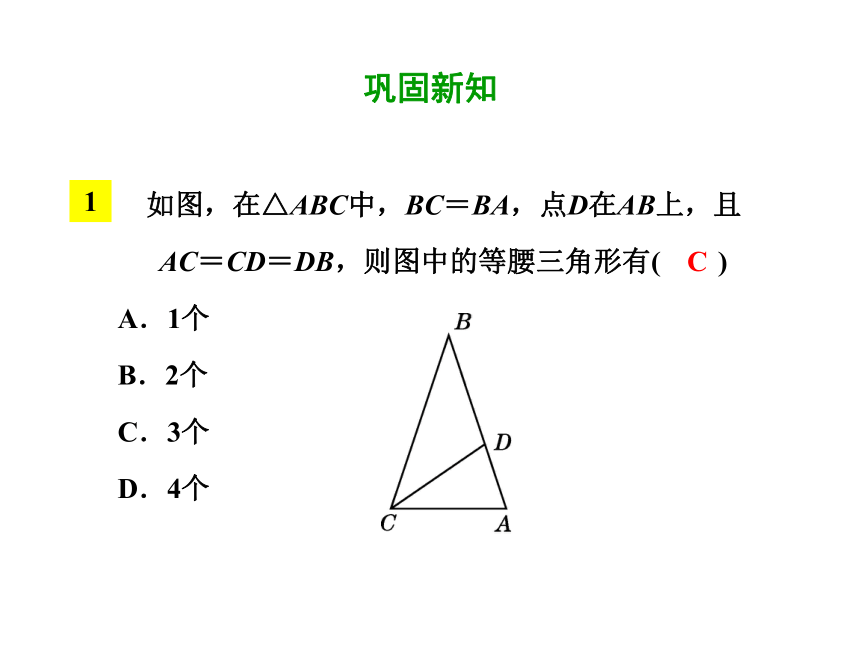
如图,在△ABC中,BC=BA,点D在AB上,且AC=CD=DB,则图中的等腰三角形有( )
A.1个
B.2个
C.3个
D.4个
C
巩固新知
2
知识点
三角形按边分类
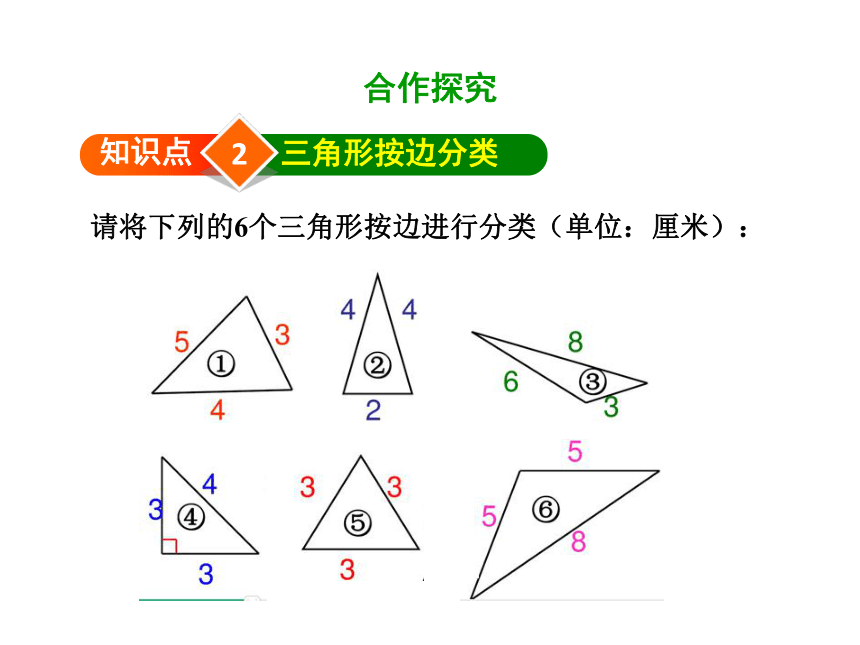
请将下列的6个三角形按边进行分类(单位:厘米):
合作探究
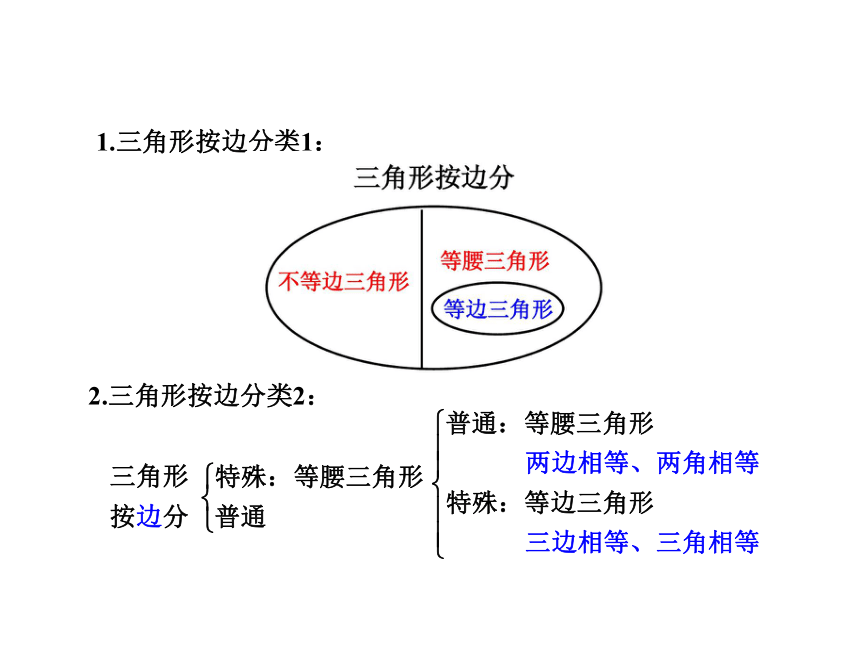
1.三角形按边分类1:
2.三角形按边分类2:
三角形
按边分
1 下列说法:
①等边三角形是等腰三角形;
②等腰三角形也可能是直角三角形;
③三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
C
巩固新知
2
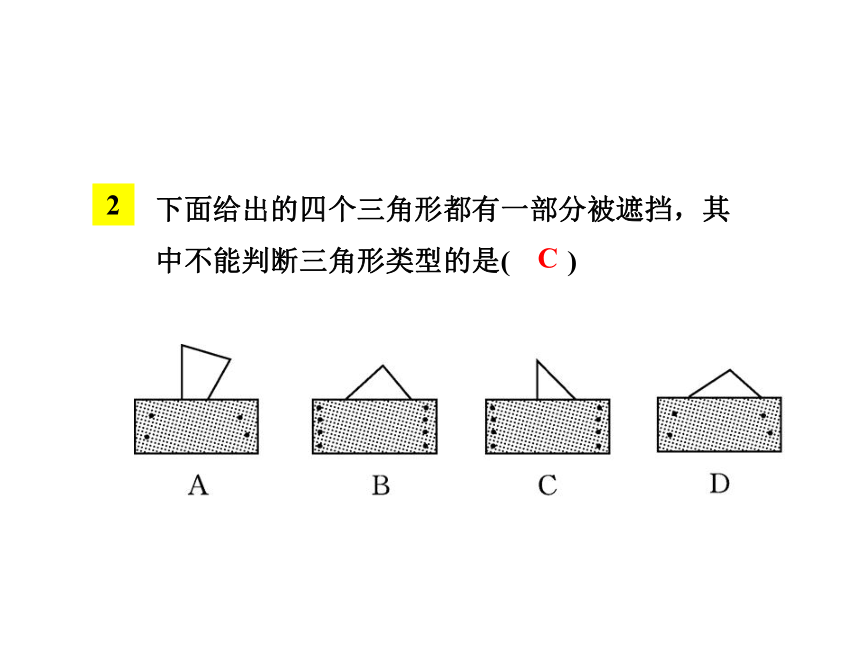
下面给出的四个三角形都有一部分被遮挡,其
中不能判断三角形类型的是( )
C
3
知识点
三角形的三边关系
议一议
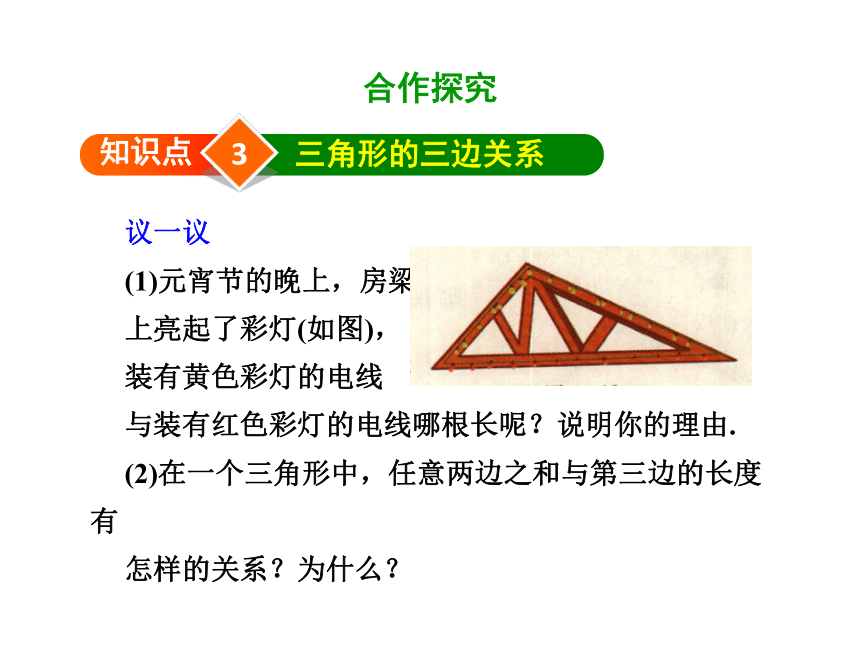
(1)元宵节的晚上,房梁
上亮起了彩灯(如图),
装有黄色彩灯的电线
与装有红色彩灯的电线哪根长呢?说明你的理由.
(2)在一个三角形中,任意两边之和与第三边的长度有
怎样的关系?为什么?
合作探究
做一做
分别量出(图4-14)三个三角形的三边长度,并填入空格内.
(1)a=________,
b=________,
c=________,
(2)a=________,
b=________,
c=________,
(3)a=________,
b=________,
c=________,
计算每个三角形的任意两边之差,并与第三边比较,
你能得到什么结论?
再画一些三角形试一试.
例2
〈温州〉下列各组数可能是一个三角形的边长的是
( )
A.1,2,4
B.4,5,9
C.4,6,8
D.5,5,11
每组数中较小两数的和与第三个数比较大小,若
较小两数的和大于第三个数,则能组成三角形.
导引:
C
判断三条线段能否组成三角形,只需看较短两
边的和是否大于第三边即可.因为只要较短两边的
和大于第三边,则任意两边的和都大于第三边,所
以用此方法可以很快地判断出三条线段能否构成三
角形.
新知小结
例3
有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
取长度为2cm的木棒时,由于
2+5=7<8,
出现了两边之和小于第三
边的情况,
所以它们不能摆成三角形.
取长度为13
cm的木棒时,由于5+8
=13,出现了两边之和等于第三边的
情况,所以它们也不能
摆成三角形.
解:
如果一根木棒能与原来的两根木棒摆成三角形,那么它的长度取值范围是什么?
合作探究
例4
一个三角形两边的长分别为5和3,第三边的长是整数,且周长是偶数,则第三边的长是( )
A.2或4
B.4或6
C.4
D.2或6
要求第三边的长,需先求出这条边长的取值范围,再
在其范围内找出满足条件的数.设三角形的第三边的
长为x,则第三边的长的取值范围为5-3<x<5+3,
即2<x<8.又在2到8之间的整数有3,4,5,6,7,而
三角形的周长x+3+5=x+8应为偶数,所以x也是偶
数,所以x的值只能是4或6,所以三角形的第三边的长
是4或6.
导引:
B
1
三角形两边长分别为3和5,第三边的长可以是8吗?可以是2吗?说说你的理由.
不可以是8,也不可以是2.理由:三角形任意两边之和大于第三边,任意两边之差小于第三边.
解:
2
在△ABC中,a=4,b=2,若第三边c的长是偶数,求c的长.
在△ABC中,a=4,b=2,所以a-b又因为c为偶数,所以c=4.
解:
巩固新知
通过多个条件确定三角形第三边的方法:
已知两边
第三边小于已知两边的和而大于已知两边的差
第三边的范围
附加条件
确定第三边
新知小结
1
【中考·淮安】若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.14
B.10
C.3
D.2
B
巩固新知
2
【中考·岳阳】下列长度的三根小木棒能构成三角形的是( )
A.2
cm,3
cm,5
cm
B.7
cm,4
cm,2
cm
C.3
cm,4
cm,8
cm
D.3
cm,3
cm,4cm
D
3
【中考·南通】下列长度的三条线段能组成三角形的是( )
A.5,6,10
B.5,6,11
C.3,4,8
D.4a,4a,8a(a>0)
A
4
【中考·金华】下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
C
5
【中考·包头】长为9,6,5,4的四根木条,选其中三根组成三角形,选法有( )
A.1种
B.2种
C.3种
D.4种
C
6
【中考·安顺】已知有理数x,y满足|x-4|+
=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16
B.20
C.16
D.以上均不对
B
7
【中考·白银】已知a,b,c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )
A.2a+2b-2c
B.2a+2b
C.2c
D.0
D
判断三条线段组成三角形的方法:
“三角形的任意两边之和大于第三边”是判断三
条线段能否组成三角形的依据,利用该性质时,通常
我们只比较较短的两边的和与最长边的大小关系,若
前者大于后者,说明可以组成三角形,否则不能组成
三角形.
1
知识小结
归纳新知
2
易错小结
【中考·贺州】一个等腰三角形的两边长分别为4,8,则它的周长为( )
A.12
B.16
C.20
D.16或20
易错点:忽视组成三角形的条件而出错
C
错解:
诊断:
D
此题出错的原因在于只注意分类讨论而忽视三角形三边关系,当腰长为4时,则三角形三边长分别为4,4,8,4+4=8,不符合三边关系,不能组成三角形;当4为底边长时,此时三角形三边长分别为4,8,8,能组成三角形.故此三角形的周长为20.
相等
相等
正三角形
课后练习
A
C
底边和腰不相等
等边
C
C
D
>
>
>
>
大于
小于
C
D
【答案】B
B
OA+OD>AD
OD+OC>CD
OBC
OB+OC>BC
2(AC+BD)>AB+BC+CD+DA
火柴棒根数
3
5
6
示意图
形状
等边三角形
等腰三角形
等边三角形
规格
1
m
2
m
3
m
4
m
5
m
6
m
价格/(元/根)
10
15
20
25
30
35
再见
第四章
认识三角形
4.1.2
三角形的三边关系
北师大版数学七年级下册
1.掌握和理解三角形的三边关系。
2.认识三角形的稳定性,并能利用三角形的稳定性解决一些实际问题。
学习目标
1.三角形的定义是什么?三角形按角分为哪几类?
2.三角形的内角和是多少度?直角三角形两锐角有何关系?
复习导入
1
知识点
等腰三角形
观察图中的三角形,你能发现它们各自的边长
之间有什么关系吗?
三角形的三边有的各不相等,有的两边相等,有的三边都相等.
合作探究
1.有两条边相等的三角形叫做等腰三角形.
2.等腰三角形中,相等的两边
都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,腰和
底边的夹角叫做底角.
例1
1.等腰三角形一腰为3cm,底为4cm,则它的周长是__________;
2.等腰三角形的一边长为3cm,另一边长为4cm,则
它的周长是______________;
3.等腰三角形的一边长为3cm,另一边长为8cm,则
它的周长是__________.
10cm
10cm或11cm
19cm
1
如图,在△ABC中,BC=BA,点D在AB上,且AC=CD=DB,则图中的等腰三角形有( )
A.1个
B.2个
C.3个
D.4个
C
巩固新知
2
知识点
三角形按边分类
请将下列的6个三角形按边进行分类(单位:厘米):
合作探究
1.三角形按边分类1:
2.三角形按边分类2:
三角形
按边分
1 下列说法:
①等边三角形是等腰三角形;
②等腰三角形也可能是直角三角形;
③三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
C
巩固新知
2
下面给出的四个三角形都有一部分被遮挡,其
中不能判断三角形类型的是( )
C
3
知识点
三角形的三边关系
议一议
(1)元宵节的晚上,房梁
上亮起了彩灯(如图),
装有黄色彩灯的电线
与装有红色彩灯的电线哪根长呢?说明你的理由.
(2)在一个三角形中,任意两边之和与第三边的长度有
怎样的关系?为什么?
合作探究
做一做
分别量出(图4-14)三个三角形的三边长度,并填入空格内.
(1)a=________,
b=________,
c=________,
(2)a=________,
b=________,
c=________,
(3)a=________,
b=________,
c=________,
计算每个三角形的任意两边之差,并与第三边比较,
你能得到什么结论?
再画一些三角形试一试.
例2
〈温州〉下列各组数可能是一个三角形的边长的是
( )
A.1,2,4
B.4,5,9
C.4,6,8
D.5,5,11
每组数中较小两数的和与第三个数比较大小,若
较小两数的和大于第三个数,则能组成三角形.
导引:
C
判断三条线段能否组成三角形,只需看较短两
边的和是否大于第三边即可.因为只要较短两边的
和大于第三边,则任意两边的和都大于第三边,所
以用此方法可以很快地判断出三条线段能否构成三
角形.
新知小结
例3
有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
取长度为2cm的木棒时,由于
2+5=7<8,
出现了两边之和小于第三
边的情况,
所以它们不能摆成三角形.
取长度为13
cm的木棒时,由于5+8
=13,出现了两边之和等于第三边的
情况,所以它们也不能
摆成三角形.
解:
如果一根木棒能与原来的两根木棒摆成三角形,那么它的长度取值范围是什么?
合作探究
例4
一个三角形两边的长分别为5和3,第三边的长是整数,且周长是偶数,则第三边的长是( )
A.2或4
B.4或6
C.4
D.2或6
要求第三边的长,需先求出这条边长的取值范围,再
在其范围内找出满足条件的数.设三角形的第三边的
长为x,则第三边的长的取值范围为5-3<x<5+3,
即2<x<8.又在2到8之间的整数有3,4,5,6,7,而
三角形的周长x+3+5=x+8应为偶数,所以x也是偶
数,所以x的值只能是4或6,所以三角形的第三边的长
是4或6.
导引:
B
1
三角形两边长分别为3和5,第三边的长可以是8吗?可以是2吗?说说你的理由.
不可以是8,也不可以是2.理由:三角形任意两边之和大于第三边,任意两边之差小于第三边.
解:
2
在△ABC中,a=4,b=2,若第三边c的长是偶数,求c的长.
在△ABC中,a=4,b=2,所以a-b
解:
巩固新知
通过多个条件确定三角形第三边的方法:
已知两边
第三边小于已知两边的和而大于已知两边的差
第三边的范围
附加条件
确定第三边
新知小结
1
【中考·淮安】若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.14
B.10
C.3
D.2
B
巩固新知
2
【中考·岳阳】下列长度的三根小木棒能构成三角形的是( )
A.2
cm,3
cm,5
cm
B.7
cm,4
cm,2
cm
C.3
cm,4
cm,8
cm
D.3
cm,3
cm,4cm
D
3
【中考·南通】下列长度的三条线段能组成三角形的是( )
A.5,6,10
B.5,6,11
C.3,4,8
D.4a,4a,8a(a>0)
A
4
【中考·金华】下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
C
5
【中考·包头】长为9,6,5,4的四根木条,选其中三根组成三角形,选法有( )
A.1种
B.2种
C.3种
D.4种
C
6
【中考·安顺】已知有理数x,y满足|x-4|+
=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16
B.20
C.16
D.以上均不对
B
7
【中考·白银】已知a,b,c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )
A.2a+2b-2c
B.2a+2b
C.2c
D.0
D
判断三条线段组成三角形的方法:
“三角形的任意两边之和大于第三边”是判断三
条线段能否组成三角形的依据,利用该性质时,通常
我们只比较较短的两边的和与最长边的大小关系,若
前者大于后者,说明可以组成三角形,否则不能组成
三角形.
1
知识小结
归纳新知
2
易错小结
【中考·贺州】一个等腰三角形的两边长分别为4,8,则它的周长为( )
A.12
B.16
C.20
D.16或20
易错点:忽视组成三角形的条件而出错
C
错解:
诊断:
D
此题出错的原因在于只注意分类讨论而忽视三角形三边关系,当腰长为4时,则三角形三边长分别为4,4,8,4+4=8,不符合三边关系,不能组成三角形;当4为底边长时,此时三角形三边长分别为4,8,8,能组成三角形.故此三角形的周长为20.
相等
相等
正三角形
课后练习
A
C
底边和腰不相等
等边
C
C
D
>
>
>
>
大于
小于
C
D
【答案】B
B
OA+OD>AD
OD+OC>CD
OBC
OB+OC>BC
2(AC+BD)>AB+BC+CD+DA
火柴棒根数
3
5
6
示意图
形状
等边三角形
等腰三角形
等边三角形
规格
1
m
2
m
3
m
4
m
5
m
6
m
价格/(元/根)
10
15
20
25
30
35
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
