2020-2021学年七年级数学苏科版下册-8.3 同底数幂的除法-课件(共15张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册-8.3 同底数幂的除法-课件(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 600.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 16:44:58 | ||
图片预览


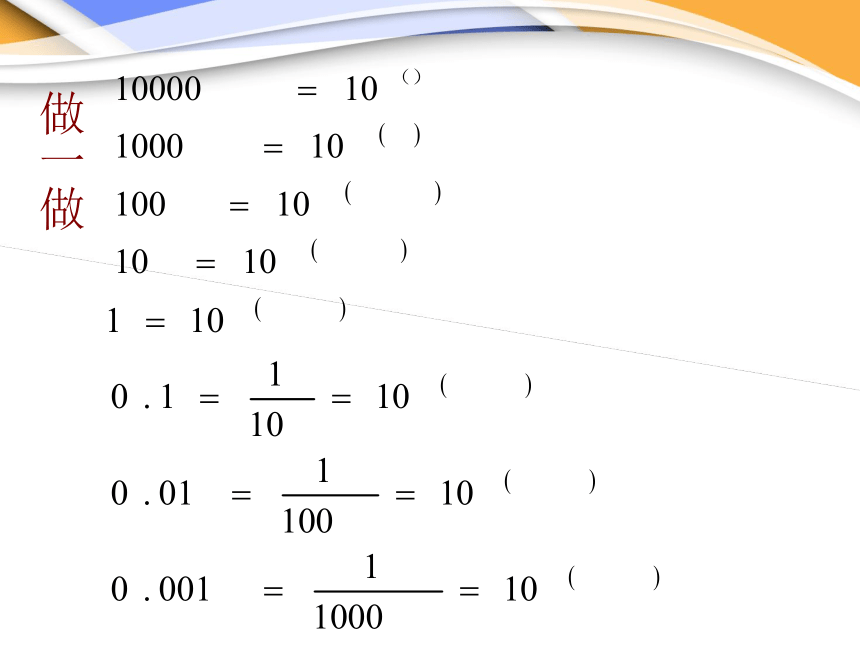




文档简介
(共15张PPT)
8.3
同底数数幂的除法(3)
知识回顾
1.零指数幂
符号语言:
文字语言:任何不等于0的数的0次幂等于0.
2.负整数指数幂
符号语言:
文字语言:任何不等于0的数的-n次幂等于这个数的n次幂的倒数.
做一做
个0
n
个0
n
(n为正整数)
请细心观察
结论:
(n为正整数)
一般地,用科学记数法可以把一个正数写成a×10n的形式,其中1≤a<10,n是整数.
结论:
说明:以前n是正整数,现在可以是0和负整数了.
例1:人体中红细胞的直径约为0.000
0077m,而流感病毒的直径约为0.000
000
08m,用科学记数法表示这两个量.
解:
0.000
0077m=7.7×10-6m
0.000
000
08m=8×10-8m
规律
小数点向右移几位,指数就是负几.
交流规律:
如何确定指数n的值?
例2:
光在真空中走30cm需要多少时间?
解:光的速度是300
000
000m/s,即3×108
m/s.
30cm,即3×10-1m.
所以,光在真空中走30cm需要的时间
为
即 光在真空中走30cm需要10-9s.
1.用科学记数法表示下列各数:
(1)0.000
0032=
(2)-0.000
00014=
(3)-680
000
000=
(4)314
000
000
000=
3.2×10-6
-1.4×10-7
-6.8×108
3.14×1011
练习:
2.写出下列用科学记数法表示的数的原来的数.
(1)2.718×106=
(2)-1.414×10-4=
2718000
-0.0001414
3.填空:
(1)若67
950
000=6.975×10m,
则m=
;
(2)若0.000
010
2=1.02×10n,
则n= .
7
-5
4.计算:
5.美国旅行者一号太空飞行器在1ns(十亿分之一秒)的时间里能飞行0.017mm,求飞行器的速度是多少m/s?
当堂检测
1.用科学记数法表示﹣0.0000059记为( )
A.﹣0.59×10﹣4
B.59×10﹣7
C.﹣5.9×10﹣6
D.﹣5.9×10﹣8
2.碳纳米管的硬度与金刚石相当,却拥有良好的柔韧性,可以拉伸,我国某物理所研究组已研制出直径为0.5nm的碳纳米管,1nm=0.000
000
001m,则0.5nm用科学记数法表示为( )
A.0.5×10﹣9
m
B.5×10﹣8
m
C.5×10﹣9
m
D.5×10﹣10
m
3.下列式子的计算中正确的个数是( )
①100÷10﹣1=10;
②10﹣4×(2×7)0=1000;
③(﹣0.1)0÷(﹣2﹣1)﹣3=8;
④(﹣10)﹣1÷(﹣10﹣1)﹣1=﹣1
A.4
B.3
C.2
D.1
4.
计算(﹣2)﹣99+(﹣4)﹣50,所得的结果为( )
A.2﹣99
B.2﹣100
C.﹣2﹣99
D.﹣2﹣100
当堂检测
5.写出原数:2.013×10﹣7=
;
用科学记数法表示:﹣0.000103=
.
6.若5a=12.5,5b=
,则3a÷3b=
.
当堂检测
8.3 同底数幂的除法(3)
谈谈本节课收获的知识与方法.
确定n的值的规律
类比
很大的数
(比1大)
很小的数
(比1小)
科学记数法
,1
≤a<10,n是整数.
8.3
同底数数幂的除法(3)
知识回顾
1.零指数幂
符号语言:
文字语言:任何不等于0的数的0次幂等于0.
2.负整数指数幂
符号语言:
文字语言:任何不等于0的数的-n次幂等于这个数的n次幂的倒数.
做一做
个0
n
个0
n
(n为正整数)
请细心观察
结论:
(n为正整数)
一般地,用科学记数法可以把一个正数写成a×10n的形式,其中1≤a<10,n是整数.
结论:
说明:以前n是正整数,现在可以是0和负整数了.
例1:人体中红细胞的直径约为0.000
0077m,而流感病毒的直径约为0.000
000
08m,用科学记数法表示这两个量.
解:
0.000
0077m=7.7×10-6m
0.000
000
08m=8×10-8m
规律
小数点向右移几位,指数就是负几.
交流规律:
如何确定指数n的值?
例2:
光在真空中走30cm需要多少时间?
解:光的速度是300
000
000m/s,即3×108
m/s.
30cm,即3×10-1m.
所以,光在真空中走30cm需要的时间
为
即 光在真空中走30cm需要10-9s.
1.用科学记数法表示下列各数:
(1)0.000
0032=
(2)-0.000
00014=
(3)-680
000
000=
(4)314
000
000
000=
3.2×10-6
-1.4×10-7
-6.8×108
3.14×1011
练习:
2.写出下列用科学记数法表示的数的原来的数.
(1)2.718×106=
(2)-1.414×10-4=
2718000
-0.0001414
3.填空:
(1)若67
950
000=6.975×10m,
则m=
;
(2)若0.000
010
2=1.02×10n,
则n= .
7
-5
4.计算:
5.美国旅行者一号太空飞行器在1ns(十亿分之一秒)的时间里能飞行0.017mm,求飞行器的速度是多少m/s?
当堂检测
1.用科学记数法表示﹣0.0000059记为( )
A.﹣0.59×10﹣4
B.59×10﹣7
C.﹣5.9×10﹣6
D.﹣5.9×10﹣8
2.碳纳米管的硬度与金刚石相当,却拥有良好的柔韧性,可以拉伸,我国某物理所研究组已研制出直径为0.5nm的碳纳米管,1nm=0.000
000
001m,则0.5nm用科学记数法表示为( )
A.0.5×10﹣9
m
B.5×10﹣8
m
C.5×10﹣9
m
D.5×10﹣10
m
3.下列式子的计算中正确的个数是( )
①100÷10﹣1=10;
②10﹣4×(2×7)0=1000;
③(﹣0.1)0÷(﹣2﹣1)﹣3=8;
④(﹣10)﹣1÷(﹣10﹣1)﹣1=﹣1
A.4
B.3
C.2
D.1
4.
计算(﹣2)﹣99+(﹣4)﹣50,所得的结果为( )
A.2﹣99
B.2﹣100
C.﹣2﹣99
D.﹣2﹣100
当堂检测
5.写出原数:2.013×10﹣7=
;
用科学记数法表示:﹣0.000103=
.
6.若5a=12.5,5b=
,则3a÷3b=
.
当堂检测
8.3 同底数幂的除法(3)
谈谈本节课收获的知识与方法.
确定n的值的规律
类比
很大的数
(比1大)
很小的数
(比1小)
科学记数法
,1
≤a<10,n是整数.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
