2020-2021学年七年级数学湘教版下册《第2章整式的乘法》高频易错专题突破训练(word版含解析)
文档属性
| 名称 | 2020-2021学年七年级数学湘教版下册《第2章整式的乘法》高频易错专题突破训练(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 51.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 10:55:07 | ||
图片预览


文档简介
2021年度湘教版七年级数学下册《第2章整式的乘法》高频易错专题突破训练(附答案)
1.a12可以写成( )
A.a6+a6
B.a2?a6
C.a6?a6
D.a12÷a
2.下列运算正确的是( )
A.a+a=a2
B.(ab)2=ab2
C.a2?a3=a5
D.(a2)3=a5
3.下列运算正确的是( )
A.x2?x3=x6
B.x2+x2=2x4
C.(﹣3a3)?(﹣5a5)=15a8
D.(﹣2x)2=﹣4x2
4.已知实数m,n,p,q满足m+n=p+q=4,mp+nq=4,则(m2+n2)pq+mn(p2+q2)=( )
A.48
B.36
C.96
D.无法计算
5.如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3
B.3
C.0
D.1
6.下列从左到右的变形,错误的是( )
A.﹣m+n=﹣(m+n)
B.﹣a﹣b=﹣(a+b)
C.(m﹣n)3=﹣(n﹣m)3
D.(y﹣x)2=(x﹣y)2
7.如图,矩形ABCD的周长是10cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为17cm2,那么矩形ABCD的面积是( )
A.3cm2
B.4cm2
C.5cm2
D.6cm2
8.已知多项式x2+4x+k2是一个完全平方式,则k的值为( )
A.2
B.4
C.2或﹣2
D.4或﹣4
9.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(2x+y)(2y﹣x)
B.(x+1)(﹣x﹣1)
C.(3x﹣y)(3x+y)
D.(x﹣y)(﹣x+y)
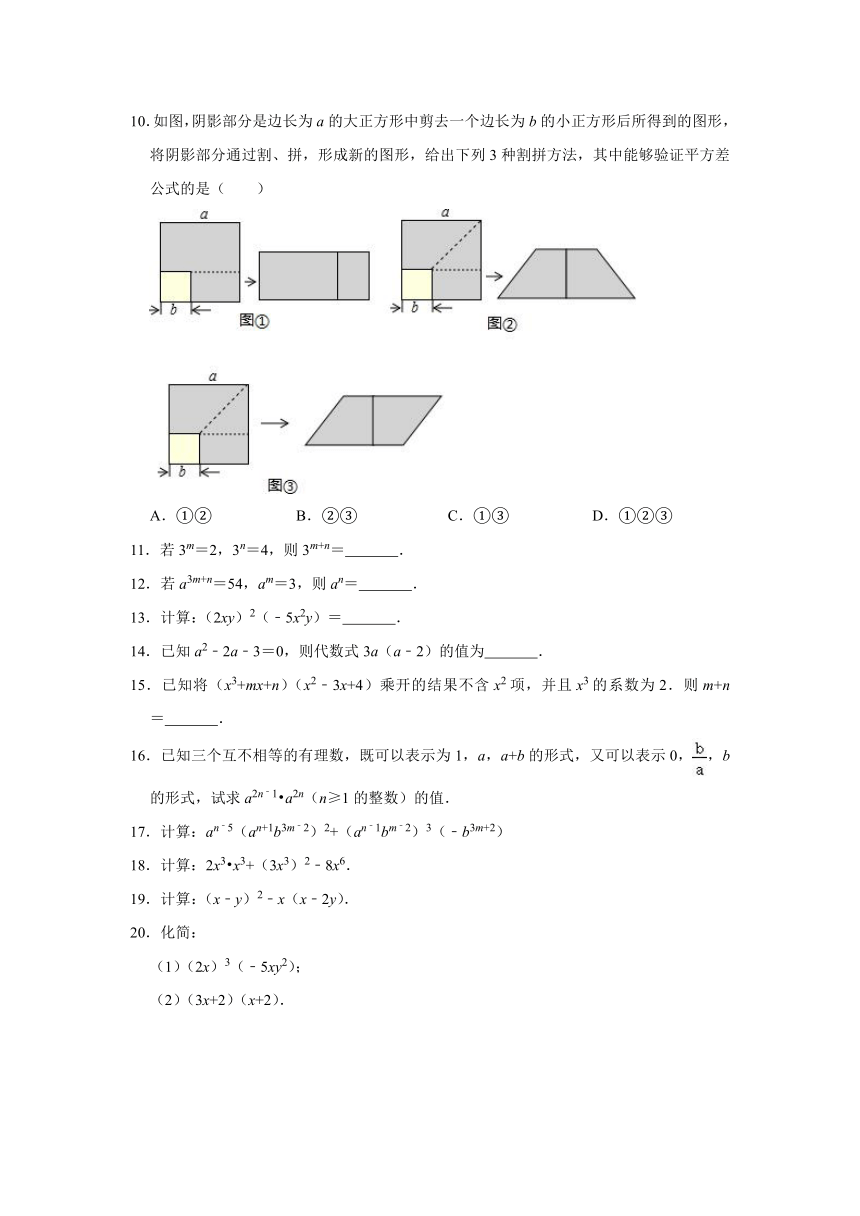
10.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )
A.①②
B.②③
C.①③
D.①②③
11.若3m=2,3n=4,则3m+n=
.
12.若a3m+n=54,am=3,则an=
.
13.计算:(2xy)2(﹣5x2y)=
.
14.已知a2﹣2a﹣3=0,则代数式3a(a﹣2)的值为
.
15.已知将(x3+mx+n)(x2﹣3x+4)乘开的结果不含x2项,并且x3的系数为2.则m+n=
.
16.已知三个互不相等的有理数,既可以表示为1,a,a+b的形式,又可以表示0,,b的形式,试求a2n﹣1?a2n(n≥1的整数)的值.
17.计算:an﹣5(an+1b3m﹣2)2+(an﹣1bm﹣2)3(﹣b3m+2)
18.计算:2x3?x3+(3x3)2﹣8x6.
19.计算:(x﹣y)2﹣x(x﹣2y).
20.化简:
(1)(2x)3(﹣5xy2);
(2)(3x+2)(x+2).
参考答案
1.解:A、a6+a6=2a6,故本选项不合题意;
B、a2?a6=a8,故本选项不合题意;
C、a6?a6=a12,故本选项符合题意;
D、a12÷a=a11,故本选项不合题意;
故选:C.
2.解:A、a+a=2a,故本选项不合题意;
B、(ab)2=a2b2,故本选项不合题意;
C、a2?a3=a5,故本选项符合题意;
D、(a2)3=a6,故本选项不合题意.
故选:C.
3.解:A、x2?x3=x5,故此选项错误;
B、x2+x2=2x2,故此选项错误;
C、(﹣3a3)?(﹣5a5)=15a8,故此选项正确;
D、(﹣2x)2=4x2,故此选项错误;
故选:C.
4.解:∵m+n=p+q=4,
∴(m+n)(p+q)=4×4=16,
∵(m+n)(p+q)=mp+mq+np+nq,
∴mp+mq+np+nq=16,
∵mp+nq=4,
∴mq+np=12,
∴(m2+n2)pq+mn(p2+q2),
=m2pq+n2pq+mnp2+mnq2,
=mp?mq+np?nq+mp?np+nq?mq,
=mp?mq+mp?np+np?nq+nq?mq,
=mp(mq+np)+nq(np+mq),
=(mp+nq)(np+mq),
=4×12,
=48,
故选:A.
5.解:∵(x+m)(x+3)=x2+3x+mx+3m=x2+(3+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴3+m=0,
解得m=﹣3.
故选:A.
6.解:A、﹣m+n=﹣(m﹣n),原变形错误,故本选项符合题意;
B、﹣a﹣b=﹣(a+b),原变形正确,故本选项不符合题意;
C、(m﹣n)3=(m﹣n)(n﹣m)2=﹣(n﹣m)(n﹣m)2=﹣(n﹣m)3,原变形正确,故本选项不符合题意;
D、(y﹣x)2=y2﹣2xy+x2=(x﹣y)2,原变形正确,故本选项不符合题意.
故选:A.
7.解:设AB=x,AD=y,
∵正方形ABEF和ADGH的面积之和为17cm2
∴x2+y2=17,
∵矩形ABCD的周长是10cm
∴2(x+y)=10,
∵(x+y)2=x2+2xy+y2,
∴25=17+2xy,
∴xy=4,
∴矩形ABCD的面积为:xy=4cm2,
故选:B.
8.解:∵多项式x2+4x+k2是一个完全平方式,
∴k=±2,
即k=2或﹣2.
故选:C.
9.解:A、(2x+y)(2y﹣x),不能用平方差公式进行计算,故本选项不符合题意;
B、(x+1)(﹣x﹣1),不能用平方差公式进行计算,故本选项不符合题意;
C、(3x﹣y)(3x+y),能用平方差公式进行计算,故本选项符合题意;
D、(x﹣y)(﹣x+y)不能用平方差公式进行计算,故本选项不符合题意;
故选:C.
10.解:在图①中,左边的图形阴影部分的面积=a2﹣b2,右边图形中阴影部分的面积=(a+b)(a﹣b),故可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;
在图②中,阴影部分的面积相等,左边阴影部分的面积=a2﹣b2,右边阴影部分面积=(2b+2a)?(a﹣b)=(a+b)(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;
在图③中,阴影部分的面积相等,左边阴影部分的面积=a2﹣b2,右边阴影部分面积=(a+b)?(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式.
故选:D.
11.解:∵3m=2,3n=4,
∴3m+n=3m?3n=2×4=8.
故答案为:8.
12.解:∵a3m+n=(am)3?an=54,am=3,
∴.
故答案为:2
13.解:原式=4x2y2?(﹣5x2y)=﹣20x4y3.
故答案为:﹣20x4y3.
14.解:∵a2﹣2a﹣3=0,
∴a2﹣2a=3,
∴3a(a﹣2)=3(a2﹣2a)=3×3=9.
故答案为:9.
15.解:(x3+mx+n)(x2﹣3x+4)
=x5﹣3x4+4x3+mx3﹣3mx2+4mx+nx2﹣3nx+4n
=x5﹣3x4+(4+m)x3+(﹣3m+n)x2+4mx﹣3nx+4n,
∵结果不含x2项,并且x3的系数为2,
∴﹣3m+n=0,4+m=2,
∴m=﹣2,n=﹣6,
∴m+n=﹣2﹣6=﹣8,
故答案为:﹣8.
16.解:由题可得:a≠0,a+b=0,
∴=﹣1,b=1,
∴a=﹣1,
又∵2n﹣1为奇数,﹣1的奇数次方得﹣1;2n为偶数,﹣1的偶数次方得1,
∴a2n﹣1?a2n=(﹣1)2n﹣1×(﹣1)2n=﹣1×1=﹣1.
17.解:原式=an﹣5(a2n+2b6m﹣4)+a3n﹣3b3m﹣6(﹣b3m+2),
=a3n﹣3b6m﹣4+a3n﹣3(﹣b6m﹣4),=a3n﹣3b6m﹣4﹣a3n﹣3b6m﹣4,=0.
18.解:2x3?x3+(3x3)2﹣8x6=2x6+9x6﹣8x6=3x6.
19.解:(x﹣y)2﹣x(x﹣2y)=x2﹣2xy+y2﹣x2+2xy=y2.
20.解:(1)原式=8x3?(﹣5xy2)=﹣8x3?5xy2=﹣40x4y2;
(2)原式=3x2+6x+2x+4=3x2+8x+4.
1.a12可以写成( )
A.a6+a6
B.a2?a6
C.a6?a6
D.a12÷a
2.下列运算正确的是( )
A.a+a=a2
B.(ab)2=ab2
C.a2?a3=a5
D.(a2)3=a5
3.下列运算正确的是( )
A.x2?x3=x6
B.x2+x2=2x4
C.(﹣3a3)?(﹣5a5)=15a8
D.(﹣2x)2=﹣4x2
4.已知实数m,n,p,q满足m+n=p+q=4,mp+nq=4,则(m2+n2)pq+mn(p2+q2)=( )
A.48
B.36
C.96
D.无法计算
5.如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3
B.3
C.0
D.1
6.下列从左到右的变形,错误的是( )
A.﹣m+n=﹣(m+n)
B.﹣a﹣b=﹣(a+b)
C.(m﹣n)3=﹣(n﹣m)3
D.(y﹣x)2=(x﹣y)2
7.如图,矩形ABCD的周长是10cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为17cm2,那么矩形ABCD的面积是( )
A.3cm2
B.4cm2
C.5cm2
D.6cm2
8.已知多项式x2+4x+k2是一个完全平方式,则k的值为( )
A.2
B.4
C.2或﹣2
D.4或﹣4
9.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(2x+y)(2y﹣x)
B.(x+1)(﹣x﹣1)
C.(3x﹣y)(3x+y)
D.(x﹣y)(﹣x+y)
10.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )
A.①②
B.②③
C.①③
D.①②③
11.若3m=2,3n=4,则3m+n=
.
12.若a3m+n=54,am=3,则an=
.
13.计算:(2xy)2(﹣5x2y)=
.
14.已知a2﹣2a﹣3=0,则代数式3a(a﹣2)的值为
.
15.已知将(x3+mx+n)(x2﹣3x+4)乘开的结果不含x2项,并且x3的系数为2.则m+n=
.
16.已知三个互不相等的有理数,既可以表示为1,a,a+b的形式,又可以表示0,,b的形式,试求a2n﹣1?a2n(n≥1的整数)的值.
17.计算:an﹣5(an+1b3m﹣2)2+(an﹣1bm﹣2)3(﹣b3m+2)
18.计算:2x3?x3+(3x3)2﹣8x6.
19.计算:(x﹣y)2﹣x(x﹣2y).
20.化简:
(1)(2x)3(﹣5xy2);
(2)(3x+2)(x+2).
参考答案
1.解:A、a6+a6=2a6,故本选项不合题意;
B、a2?a6=a8,故本选项不合题意;
C、a6?a6=a12,故本选项符合题意;
D、a12÷a=a11,故本选项不合题意;
故选:C.
2.解:A、a+a=2a,故本选项不合题意;
B、(ab)2=a2b2,故本选项不合题意;
C、a2?a3=a5,故本选项符合题意;
D、(a2)3=a6,故本选项不合题意.
故选:C.
3.解:A、x2?x3=x5,故此选项错误;
B、x2+x2=2x2,故此选项错误;
C、(﹣3a3)?(﹣5a5)=15a8,故此选项正确;
D、(﹣2x)2=4x2,故此选项错误;
故选:C.
4.解:∵m+n=p+q=4,
∴(m+n)(p+q)=4×4=16,
∵(m+n)(p+q)=mp+mq+np+nq,
∴mp+mq+np+nq=16,
∵mp+nq=4,
∴mq+np=12,
∴(m2+n2)pq+mn(p2+q2),
=m2pq+n2pq+mnp2+mnq2,
=mp?mq+np?nq+mp?np+nq?mq,
=mp?mq+mp?np+np?nq+nq?mq,
=mp(mq+np)+nq(np+mq),
=(mp+nq)(np+mq),
=4×12,
=48,
故选:A.
5.解:∵(x+m)(x+3)=x2+3x+mx+3m=x2+(3+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴3+m=0,
解得m=﹣3.
故选:A.
6.解:A、﹣m+n=﹣(m﹣n),原变形错误,故本选项符合题意;
B、﹣a﹣b=﹣(a+b),原变形正确,故本选项不符合题意;
C、(m﹣n)3=(m﹣n)(n﹣m)2=﹣(n﹣m)(n﹣m)2=﹣(n﹣m)3,原变形正确,故本选项不符合题意;
D、(y﹣x)2=y2﹣2xy+x2=(x﹣y)2,原变形正确,故本选项不符合题意.
故选:A.
7.解:设AB=x,AD=y,
∵正方形ABEF和ADGH的面积之和为17cm2
∴x2+y2=17,
∵矩形ABCD的周长是10cm
∴2(x+y)=10,
∵(x+y)2=x2+2xy+y2,
∴25=17+2xy,
∴xy=4,
∴矩形ABCD的面积为:xy=4cm2,
故选:B.
8.解:∵多项式x2+4x+k2是一个完全平方式,
∴k=±2,
即k=2或﹣2.
故选:C.
9.解:A、(2x+y)(2y﹣x),不能用平方差公式进行计算,故本选项不符合题意;
B、(x+1)(﹣x﹣1),不能用平方差公式进行计算,故本选项不符合题意;
C、(3x﹣y)(3x+y),能用平方差公式进行计算,故本选项符合题意;
D、(x﹣y)(﹣x+y)不能用平方差公式进行计算,故本选项不符合题意;
故选:C.
10.解:在图①中,左边的图形阴影部分的面积=a2﹣b2,右边图形中阴影部分的面积=(a+b)(a﹣b),故可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;
在图②中,阴影部分的面积相等,左边阴影部分的面积=a2﹣b2,右边阴影部分面积=(2b+2a)?(a﹣b)=(a+b)(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;
在图③中,阴影部分的面积相等,左边阴影部分的面积=a2﹣b2,右边阴影部分面积=(a+b)?(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式.
故选:D.
11.解:∵3m=2,3n=4,
∴3m+n=3m?3n=2×4=8.
故答案为:8.
12.解:∵a3m+n=(am)3?an=54,am=3,
∴.
故答案为:2
13.解:原式=4x2y2?(﹣5x2y)=﹣20x4y3.
故答案为:﹣20x4y3.
14.解:∵a2﹣2a﹣3=0,
∴a2﹣2a=3,
∴3a(a﹣2)=3(a2﹣2a)=3×3=9.
故答案为:9.
15.解:(x3+mx+n)(x2﹣3x+4)
=x5﹣3x4+4x3+mx3﹣3mx2+4mx+nx2﹣3nx+4n
=x5﹣3x4+(4+m)x3+(﹣3m+n)x2+4mx﹣3nx+4n,
∵结果不含x2项,并且x3的系数为2,
∴﹣3m+n=0,4+m=2,
∴m=﹣2,n=﹣6,
∴m+n=﹣2﹣6=﹣8,
故答案为:﹣8.
16.解:由题可得:a≠0,a+b=0,
∴=﹣1,b=1,
∴a=﹣1,
又∵2n﹣1为奇数,﹣1的奇数次方得﹣1;2n为偶数,﹣1的偶数次方得1,
∴a2n﹣1?a2n=(﹣1)2n﹣1×(﹣1)2n=﹣1×1=﹣1.
17.解:原式=an﹣5(a2n+2b6m﹣4)+a3n﹣3b3m﹣6(﹣b3m+2),
=a3n﹣3b6m﹣4+a3n﹣3(﹣b6m﹣4),=a3n﹣3b6m﹣4﹣a3n﹣3b6m﹣4,=0.
18.解:2x3?x3+(3x3)2﹣8x6=2x6+9x6﹣8x6=3x6.
19.解:(x﹣y)2﹣x(x﹣2y)=x2﹣2xy+y2﹣x2+2xy=y2.
20.解:(1)原式=8x3?(﹣5xy2)=﹣8x3?5xy2=﹣40x4y2;
(2)原式=3x2+6x+2x+4=3x2+8x+4.
