2020—2021学年人教版数学八年级下册18.2.1矩形课件(共14张ppt)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册18.2.1矩形课件(共14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
第十八章
平行四边形
18.2
特殊的平行四边形
18.2.1
矩
形
细心观察
矩形的定义和性质
在推动平行四边形的过程中,什么发生变化了?什么没变?有没有熟悉的、特殊的图形?
矩形的定义和性质
学习新知
矩形的定义:
有一个角是直角的平行四边形是矩形
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
学习探究
思考:矩形具有平行四边形所有的性质外,还有哪些特有的性质?
矩形的四个角都是直角
矩形的对角线相等
提出猜想:
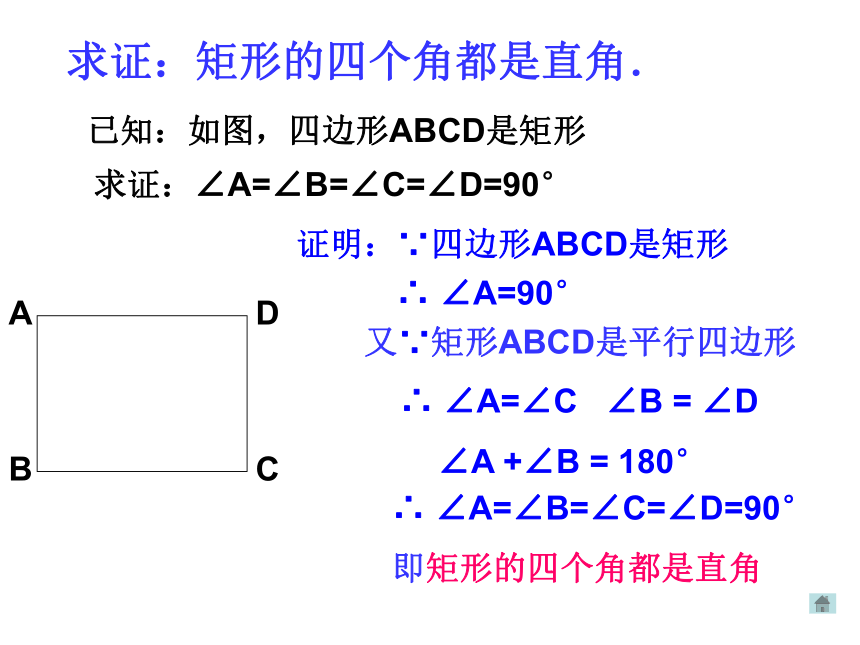
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:∵四边形ABCD是矩形
∴
∠A=90°
又∵矩形ABCD是平行四边形
∴
∠A=∠C
∠B
=
∠D
∠A
+∠B
=
180°
∴
∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
A
O
D
C
B
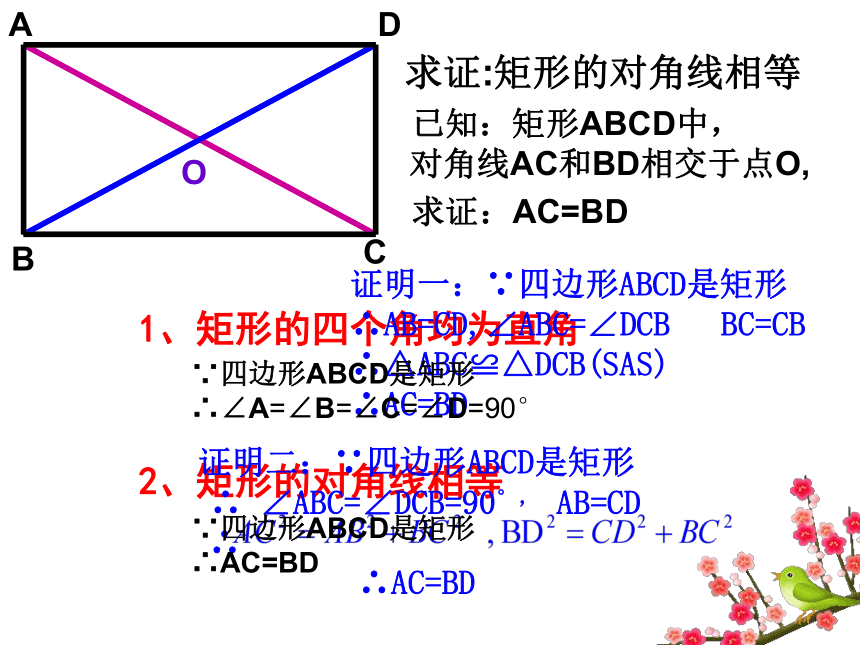
求证:矩形的对角线相等
已知:矩形ABCD中,
对角线AC和BD相交于点O,
求证:AC=BD
1、矩形的四个角均为直角
2、矩形的对角线相等
证明二:∵四边形ABCD是矩形
∴
∠ABC=∠DCB=90°,
AB=CD
∴
∴AC=BD
证明一:∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB
BC=CB
∴△ABC≌△DCB(SAS)
∴AC=BD
∵四边形ABCD是矩形∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是矩形∴AC=BD
A
B
C
D
O
◆
两对全等的等腰三角形.
你在矩形中还发现了哪些基本图形?
◆
四个全等的直角三角形.
学以致用
矩形的定义和性质
1.
矩形具有而一般平行四边形不具有的性质是(
).
A、对角线相等
B、对边相等
C、对角相等
D、对角线互相平分
2、
矩形的一组邻边长分别是3cm和4cm,
则它的对角线长是
cm.
A
5
A
O
D
C
B
矩形的定义和性质
学有所得
观察图中的Rt△ABC,
在Rt△ABC中,BO是
斜边AC上的中线,BO
与AC有什么关系?
根据矩形的性质,可以得到:
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
学例题,知方法
矩形的定义和性质
C
O
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.
∴OA=OB,
∵∠COD=∠AOB=60°,
∴OA=AB=4
∴矩形的对角线AC=BD=2OA=8
∴△AOB是等边三角形
已知:
如图,矩形ABCD的
两条对角线交于点O,
AB=
4,∠COD=60°。
求矩形对角线的长。
A
B
D
试一试,你能行
矩形的定义和性质
1、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____
A
D
C
B
O
16
矩形的定义和性质
3、直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;
1、矩形定义:
有一个角是直角的平行四边形叫矩形
边:矩形的对边平行且相等
角:矩形的四个角均为直角
2、矩形
对角线:矩形的对角线互相平分且相等
课堂小结
作
业
1、
习题18.2
19
矩形
1、2、3
P53练习题
练习册
第十八章
平行四边形
18.2
特殊的平行四边形
18.2.1
矩
形
细心观察
矩形的定义和性质
在推动平行四边形的过程中,什么发生变化了?什么没变?有没有熟悉的、特殊的图形?
矩形的定义和性质
学习新知
矩形的定义:
有一个角是直角的平行四边形是矩形
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
学习探究
思考:矩形具有平行四边形所有的性质外,还有哪些特有的性质?
矩形的四个角都是直角
矩形的对角线相等
提出猜想:
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:∵四边形ABCD是矩形
∴
∠A=90°
又∵矩形ABCD是平行四边形
∴
∠A=∠C
∠B
=
∠D
∠A
+∠B
=
180°
∴
∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
A
O
D
C
B
求证:矩形的对角线相等
已知:矩形ABCD中,
对角线AC和BD相交于点O,
求证:AC=BD
1、矩形的四个角均为直角
2、矩形的对角线相等
证明二:∵四边形ABCD是矩形
∴
∠ABC=∠DCB=90°,
AB=CD
∴
∴AC=BD
证明一:∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB
BC=CB
∴△ABC≌△DCB(SAS)
∴AC=BD
∵四边形ABCD是矩形∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是矩形∴AC=BD
A
B
C
D
O
◆
两对全等的等腰三角形.
你在矩形中还发现了哪些基本图形?
◆
四个全等的直角三角形.
学以致用
矩形的定义和性质
1.
矩形具有而一般平行四边形不具有的性质是(
).
A、对角线相等
B、对边相等
C、对角相等
D、对角线互相平分
2、
矩形的一组邻边长分别是3cm和4cm,
则它的对角线长是
cm.
A
5
A
O
D
C
B
矩形的定义和性质
学有所得
观察图中的Rt△ABC,
在Rt△ABC中,BO是
斜边AC上的中线,BO
与AC有什么关系?
根据矩形的性质,可以得到:
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
学例题,知方法
矩形的定义和性质
C
O
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.
∴OA=OB,
∵∠COD=∠AOB=60°,
∴OA=AB=4
∴矩形的对角线AC=BD=2OA=8
∴△AOB是等边三角形
已知:
如图,矩形ABCD的
两条对角线交于点O,
AB=
4,∠COD=60°。
求矩形对角线的长。
A
B
D
试一试,你能行
矩形的定义和性质
1、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____
A
D
C
B
O
16
矩形的定义和性质
3、直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;
1、矩形定义:
有一个角是直角的平行四边形叫矩形
边:矩形的对边平行且相等
角:矩形的四个角均为直角
2、矩形
对角线:矩形的对角线互相平分且相等
课堂小结
作
业
1、
习题18.2
19
矩形
1、2、3
P53练习题
练习册
