3.1.2圆周角导学案
图片预览
文档简介
编号05 九年级数学(下)导学案
课题:3.1.2圆周角 九年级数学 执笔人:
学习目标:理解圆周角的概念及它与圆心角、弧、弦的关系
学习内容 学习方式、方法
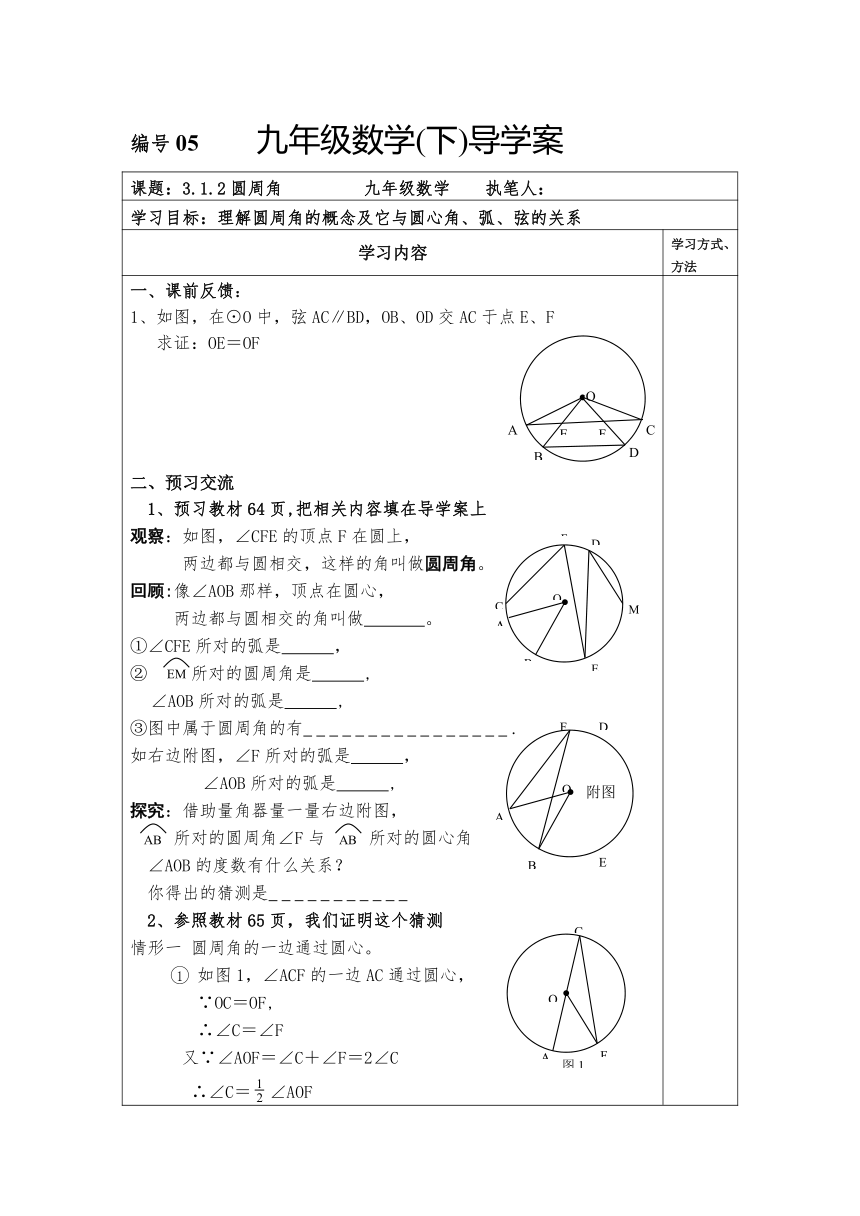
一、课前反馈:1、如图,在⊙O中,弦AC∥BD,OB、OD交AC于点E、F 求证:OE=OF二、预习交流 1、预习教材64页,把相关内容填在导学案上观察:如图,∠CFE的顶点F在圆上,两边都与圆相交,这样的角叫做圆周角。回顾:像∠AOB那样,顶点在圆心,两边都与圆相交的角叫做 。①∠CFE所对的弧是 ,② 所对的圆周角是 , ∠AOB所对的弧是 ,③图中属于圆周角的有 .如右边附图,∠F所对的弧是 , ∠AOB所对的弧是 ,探究:借助量角器量一量右边附图, 所对的圆周角∠F与 所对的圆心角∠AOB的度数有什么关系? 你得出的猜测是 2、参照教材65页,我们证明这个猜测情形一 圆周角的一边通过圆心。如图1,∠ACF的一边AC通过圆心,∵OC=OF,∴∠C=∠F 又∵∠AOF=∠C+∠F=2∠C ∴∠C=∠AOF
学习内容 学习方式、方法
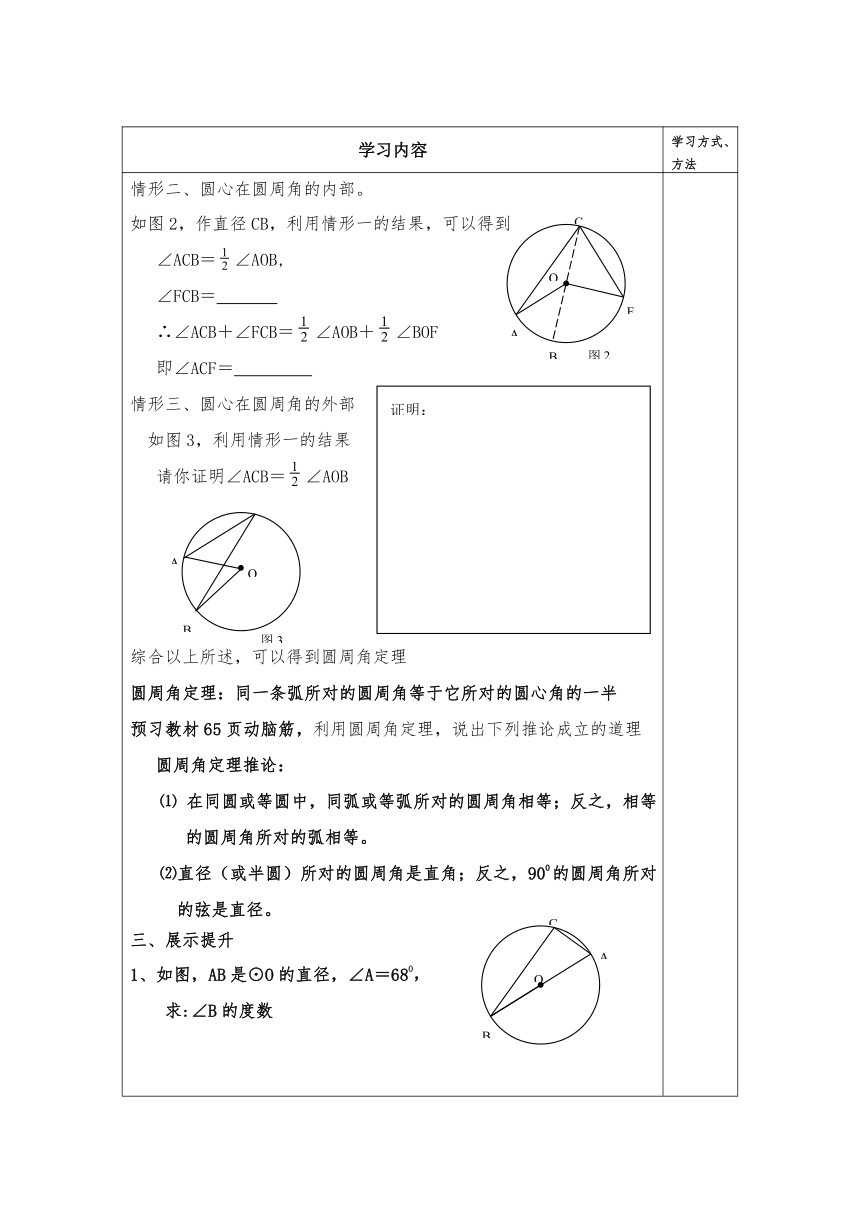
情形二、圆心在圆周角的内部。如图2,作直径CB,利用情形一的结果,可以得到 ∠ACB=∠AOB, ∠FCB= ∴∠ACB+∠FCB=∠AOB+∠BOF 即∠ACF= 情形三、圆心在圆周角的外部如图3,利用情形一的结果请你证明∠ACB=∠AOB 综合以上所述,可以得到圆周角定理圆周角定理:同一条弧所对的圆周角等于它所对的圆心角的一半预习教材65页动脑筋,利用圆周角定理,说出下列推论成立的道理圆周角定理推论:⑴ 在同圆或等圆中,同弧或等弧所对的圆周角相等;反之,相等的圆周角所对的弧相等。⑵直径(或半圆)所对的圆周角是直角;反之,90O的圆周角所对的弦是直径。三、展示提升1、如图,AB是⊙O的直径,∠A=68O,求:∠B的度数 2、如图5,弦AF∥DB,求证:∠C=∠E3、如图,AC是⊙O的直径,弦AD=AB,求证:CD=CB四、梳理巩固:1、同一条弧所对的圆周角等于 一半;①直径所对的圆周角是直角;90O的圆周角所对的弦是 。②在同圆或等圆中,同弧或等弧所对的圆周角相等;反之,相等的圆周角所对的弧相等。2、 叫做等圆;3、圆既是旋转对称图形,绕圆心旋转 ,都能与自身重合;又是 ,圆心是它的对称中心;圆有 条对称轴,任意一条 都是它的对称轴。4、在同圆或等圆中,两个圆心角、两条弧、两条弦,如果有一组量相等,那么它们对应的其余各组量也 。5、 直径平分这条弦,并且平分 优弧和劣弧。6、圆的两条平行线所夹的弧 。五、当堂检测:1、如图,点A,B,C,在圆O上,∠A=70O,求∠OCB的度数2、如图6,△ABC的顶点在圆上,AD为直径,AD⊥CE,垂足为F,求证:AC2=AB·AE3、如图⊙O的两条弦AB、CD相交于点F,求证:FA·FB=FC·FD (这个结论被称为相交弦定理)4、已知⊙O的半径为17cm,弦AB⊥CD,垂足为F,AF=18cm,BF=12cm,求:OF的长度、CD的长度
自留地
C
B
D
A
O
E
F
A
F
E
C
B
O
M
D
EM
F
E
B
O
附图
A
D
F
E
B
O
附图
A
D
AB
AB
图1
F
A
C
O
B
图2
F
A
C
O
证明:
B
图3
A
C
O
B
A
C
O
E
D
图5
F
A
C
O
B
D
B
A
C
O
B
A
C
O
B
E
图6
F
A
C
O
D
A
B
D
O
C
F
A
B
D
O
C
F
课题:3.1.2圆周角 九年级数学 执笔人:
学习目标:理解圆周角的概念及它与圆心角、弧、弦的关系
学习内容 学习方式、方法
一、课前反馈:1、如图,在⊙O中,弦AC∥BD,OB、OD交AC于点E、F 求证:OE=OF二、预习交流 1、预习教材64页,把相关内容填在导学案上观察:如图,∠CFE的顶点F在圆上,两边都与圆相交,这样的角叫做圆周角。回顾:像∠AOB那样,顶点在圆心,两边都与圆相交的角叫做 。①∠CFE所对的弧是 ,② 所对的圆周角是 , ∠AOB所对的弧是 ,③图中属于圆周角的有 .如右边附图,∠F所对的弧是 , ∠AOB所对的弧是 ,探究:借助量角器量一量右边附图, 所对的圆周角∠F与 所对的圆心角∠AOB的度数有什么关系? 你得出的猜测是 2、参照教材65页,我们证明这个猜测情形一 圆周角的一边通过圆心。如图1,∠ACF的一边AC通过圆心,∵OC=OF,∴∠C=∠F 又∵∠AOF=∠C+∠F=2∠C ∴∠C=∠AOF
学习内容 学习方式、方法
情形二、圆心在圆周角的内部。如图2,作直径CB,利用情形一的结果,可以得到 ∠ACB=∠AOB, ∠FCB= ∴∠ACB+∠FCB=∠AOB+∠BOF 即∠ACF= 情形三、圆心在圆周角的外部如图3,利用情形一的结果请你证明∠ACB=∠AOB 综合以上所述,可以得到圆周角定理圆周角定理:同一条弧所对的圆周角等于它所对的圆心角的一半预习教材65页动脑筋,利用圆周角定理,说出下列推论成立的道理圆周角定理推论:⑴ 在同圆或等圆中,同弧或等弧所对的圆周角相等;反之,相等的圆周角所对的弧相等。⑵直径(或半圆)所对的圆周角是直角;反之,90O的圆周角所对的弦是直径。三、展示提升1、如图,AB是⊙O的直径,∠A=68O,求:∠B的度数 2、如图5,弦AF∥DB,求证:∠C=∠E3、如图,AC是⊙O的直径,弦AD=AB,求证:CD=CB四、梳理巩固:1、同一条弧所对的圆周角等于 一半;①直径所对的圆周角是直角;90O的圆周角所对的弦是 。②在同圆或等圆中,同弧或等弧所对的圆周角相等;反之,相等的圆周角所对的弧相等。2、 叫做等圆;3、圆既是旋转对称图形,绕圆心旋转 ,都能与自身重合;又是 ,圆心是它的对称中心;圆有 条对称轴,任意一条 都是它的对称轴。4、在同圆或等圆中,两个圆心角、两条弧、两条弦,如果有一组量相等,那么它们对应的其余各组量也 。5、 直径平分这条弦,并且平分 优弧和劣弧。6、圆的两条平行线所夹的弧 。五、当堂检测:1、如图,点A,B,C,在圆O上,∠A=70O,求∠OCB的度数2、如图6,△ABC的顶点在圆上,AD为直径,AD⊥CE,垂足为F,求证:AC2=AB·AE3、如图⊙O的两条弦AB、CD相交于点F,求证:FA·FB=FC·FD (这个结论被称为相交弦定理)4、已知⊙O的半径为17cm,弦AB⊥CD,垂足为F,AF=18cm,BF=12cm,求:OF的长度、CD的长度
自留地
C
B
D
A
O
E
F
A
F
E
C
B
O
M
D
EM
F
E
B
O
附图
A
D
F
E
B
O
附图
A
D
AB
AB
图1
F
A
C
O
B
图2
F
A
C
O
证明:
B
图3
A
C
O
B
A
C
O
E
D
图5
F
A
C
O
B
D
B
A
C
O
B
A
C
O
B
E
图6
F
A
C
O
D
A
B
D
O
C
F
A
B
D
O
C
F
