3.3圆与圆的位置关系导学案
图片预览

文档简介
编号012 九年级数学(下)导学案
课题:3.3 圆与圆的位置关系 九年级数学 执笔人:
学习目标:会判断圆与圆的位置关系
学习内容 学习方式、方法
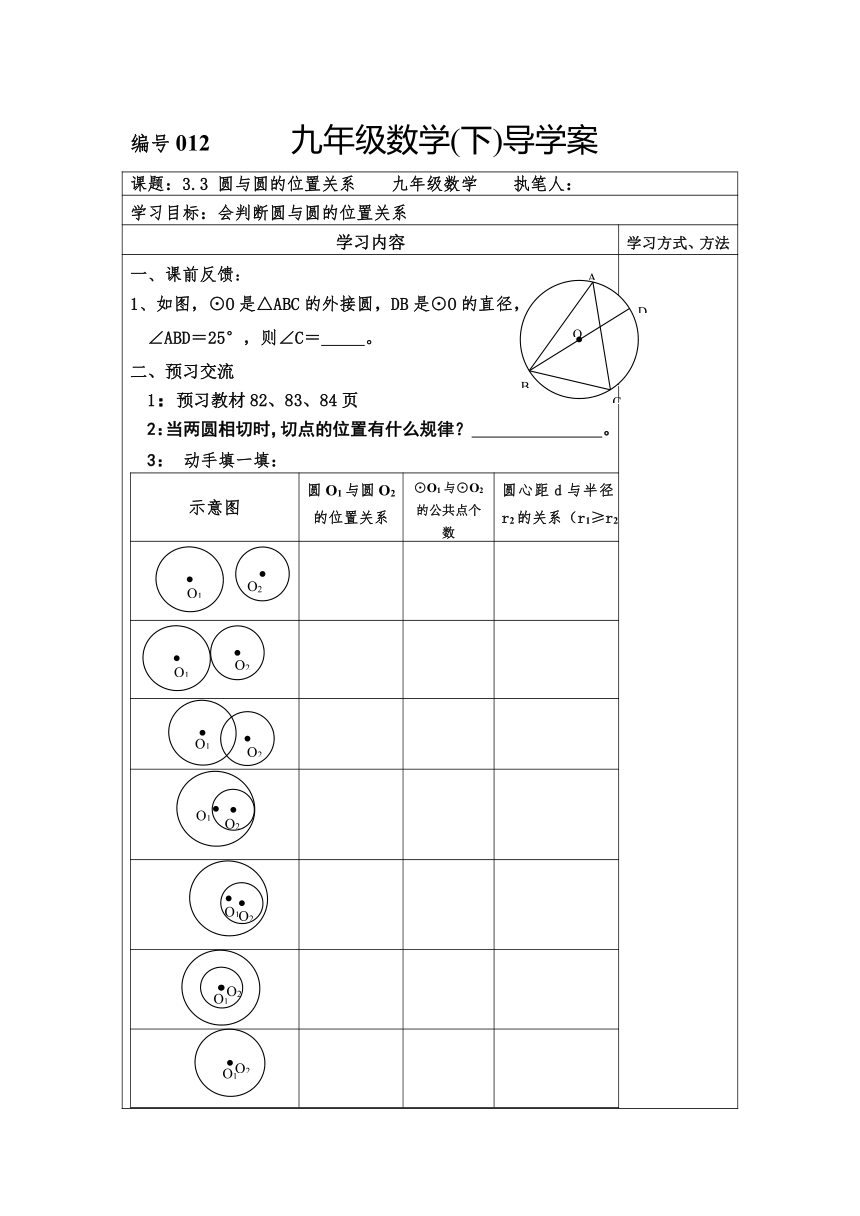
一、课前反馈:1、如图,⊙O是△ABC的外接圆,DB是⊙O的直径,∠ABD=25°,则∠C= 。二、预习交流1:预习教材82、83、84页2:当两圆相切时,切点的位置有什么规律? 。3: 动手填一填:示意图圆O1与圆O2的位置关系⊙O1与⊙O2的公共点个数圆心距d与半径r1、r2的关系(r1≥r2)
学习内容 学习方式、方法
三、展示提升1、已知⊙O1与⊙O2外切,圆心距d=15cm,半径r1=4cm,则r2= 。2、⊙O1与⊙O2的半径r1为4 cm、r2为9 cm,当圆心距d分别为下列值时,判断两圆的位置关系。① d=16cm ② d=7cm ③ d=5cm3、已知⊙O1与⊙O2内切,半径r1=14cm,r2=8 cm,连心线与⊙O1交于点A、C,与⊙O2交于点A、B,求:线段BC的长度。四、梳理巩固:1、⊙O1与⊙O2的圆心距为d,半径分别为r1、r2,(r1≥r2),当⊙O1与圆O2只有一个公共点时,圆心距d与半径r1、r2的关系是 。2、如果上述两圆相交,则d与r1、r2的关系是 。五、复习与检测:1、如图,⊙O与△ABC相切于点F、K、E,且点A、B、C都在⊙P上 那么⊙O叫做△ABC的 ,△ABC叫做⊙O的 .⊙P叫做△ABC的 ,△ABC叫做⊙P的 .点O、P分别叫做△ABC的 、 。2、如图,△ABC内接于⊙O,∠CAE=∠B,求证:直线AE是⊙O的切线。3、AB是⊙O的直径,C是⊙O上的一点,过点C作⊙O的切线CD,作BD⊥CD,交AC的延长线于点E,求证:AB=BE4、如图,已知⊙O是△ABC的内切圆,∠C=90O,AC=4cm,BC=3cm,求:内切圆⊙O的面积5、如图AF是⊙O的半径,BC切⊙O于点B,CE垂直于AF,垂足为E,交AB于点D,求证:CD=CB6、如图,已知两个同心圆O,AB切大圆于点B,AC切小圆于点C,交大圆于点D、E,AB=24,AO=30,AD=16. 求:大圆、小圆的半径7、在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长与BC的延长线交于点F。⑴ 求证:BD=BF;⑵ 如果BC=6,AD=4,求⊙O的面积
自留地
B
C
A
O
D
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
A
B
C
K
C
B
E
A
O
F
P
B
A
O
E
C
A
D
B
E
C
O
B
C
A
o
A
D
B
E
C
O
E
D
B
A
O
C
B
A
D
O
C
E
F
课题:3.3 圆与圆的位置关系 九年级数学 执笔人:
学习目标:会判断圆与圆的位置关系
学习内容 学习方式、方法
一、课前反馈:1、如图,⊙O是△ABC的外接圆,DB是⊙O的直径,∠ABD=25°,则∠C= 。二、预习交流1:预习教材82、83、84页2:当两圆相切时,切点的位置有什么规律? 。3: 动手填一填:示意图圆O1与圆O2的位置关系⊙O1与⊙O2的公共点个数圆心距d与半径r1、r2的关系(r1≥r2)
学习内容 学习方式、方法
三、展示提升1、已知⊙O1与⊙O2外切,圆心距d=15cm,半径r1=4cm,则r2= 。2、⊙O1与⊙O2的半径r1为4 cm、r2为9 cm,当圆心距d分别为下列值时,判断两圆的位置关系。① d=16cm ② d=7cm ③ d=5cm3、已知⊙O1与⊙O2内切,半径r1=14cm,r2=8 cm,连心线与⊙O1交于点A、C,与⊙O2交于点A、B,求:线段BC的长度。四、梳理巩固:1、⊙O1与⊙O2的圆心距为d,半径分别为r1、r2,(r1≥r2),当⊙O1与圆O2只有一个公共点时,圆心距d与半径r1、r2的关系是 。2、如果上述两圆相交,则d与r1、r2的关系是 。五、复习与检测:1、如图,⊙O与△ABC相切于点F、K、E,且点A、B、C都在⊙P上 那么⊙O叫做△ABC的 ,△ABC叫做⊙O的 .⊙P叫做△ABC的 ,△ABC叫做⊙P的 .点O、P分别叫做△ABC的 、 。2、如图,△ABC内接于⊙O,∠CAE=∠B,求证:直线AE是⊙O的切线。3、AB是⊙O的直径,C是⊙O上的一点,过点C作⊙O的切线CD,作BD⊥CD,交AC的延长线于点E,求证:AB=BE4、如图,已知⊙O是△ABC的内切圆,∠C=90O,AC=4cm,BC=3cm,求:内切圆⊙O的面积5、如图AF是⊙O的半径,BC切⊙O于点B,CE垂直于AF,垂足为E,交AB于点D,求证:CD=CB6、如图,已知两个同心圆O,AB切大圆于点B,AC切小圆于点C,交大圆于点D、E,AB=24,AO=30,AD=16. 求:大圆、小圆的半径7、在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长与BC的延长线交于点F。⑴ 求证:BD=BF;⑵ 如果BC=6,AD=4,求⊙O的面积
自留地
B
C
A
O
D
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
A
B
C
K
C
B
E
A
O
F
P
B
A
O
E
C
A
D
B
E
C
O
B
C
A
o
A
D
B
E
C
O
E
D
B
A
O
C
B
A
D
O
C
E
F
