9.2.1向量的加减法-【新教材】2020-2021学年苏教版(2019)高中数学必修第二册同步教案(学生版+教师版)
文档属性
| 名称 | 9.2.1向量的加减法-【新教材】2020-2021学年苏教版(2019)高中数学必修第二册同步教案(学生版+教师版) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 18:49:54 | ||
图片预览




文档简介
编号:002
课题:§9.2.1
向量的加减法
目标要求
1、理解并掌握向量的概念.
2、理解并掌握零向量与单位向量.
3、理解并掌握相等向量与共线向量.
4、理解并掌握向量的应用.
学科素养目标
向量注重“形”,是几何学的基础,广泛应用于实际生活和生产中.通过数形结合,了解向量知识在高中阶段的作用.
重点难点
重点:相等向量与共线向量;
难点:向量的应用.
教学过程
基础知识点
1.向量加法的定义
求____________________的运算,叫作向量的加法.
2.求向量和的方法
(1)三角形法则与平行四边形法则
三角
形法
则
作法
已知向量和,在平面内任取一点O,
作,则向量叫作与
的和,记作,即.
图示
平行
四边
形法
则
作法
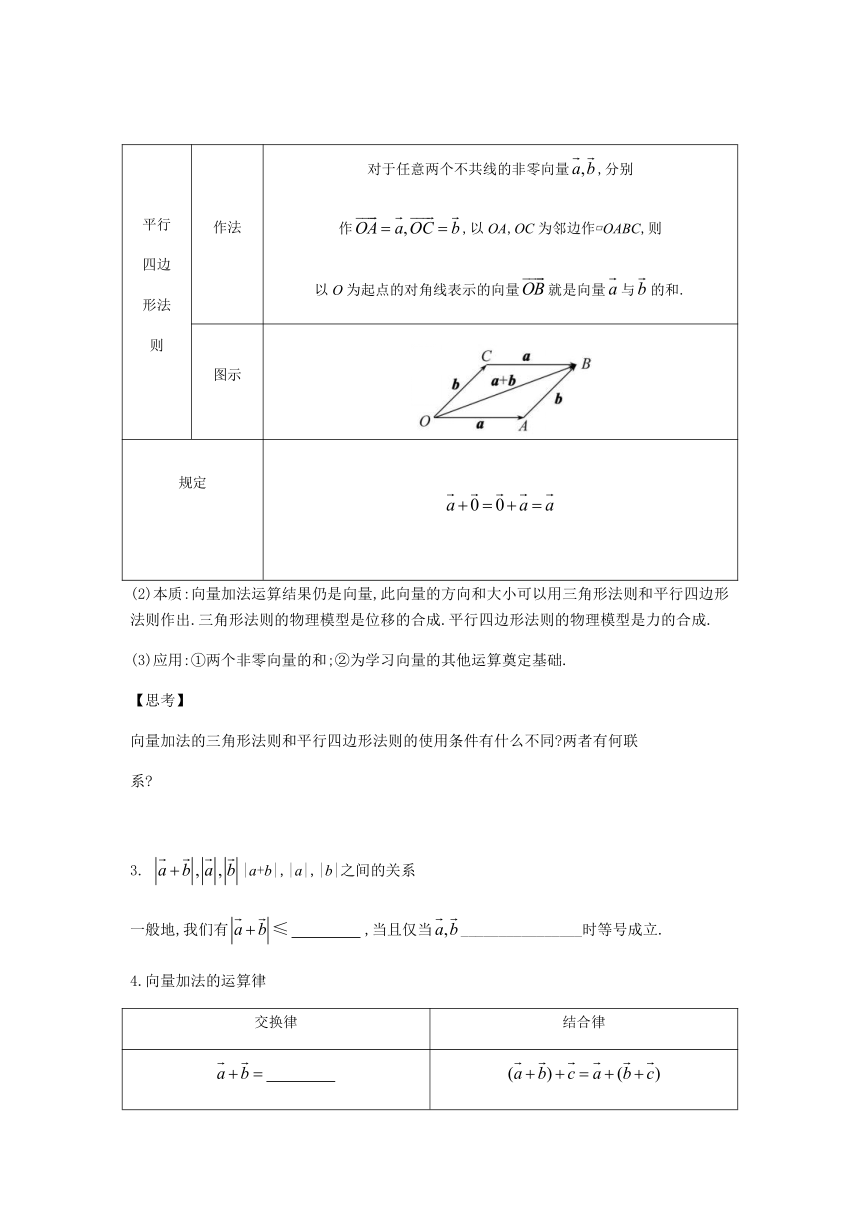
对于任意两个不共线的非零向量,分别
作,以OA,OC为邻边作?OABC,则
以O为起点的对角线表示的向量就是向量与的和.
图示
规定
(2)本质:向量加法运算结果仍是向量,此向量的方向和大小可以用三角形法则和平行四边形法则作出.三角形法则的物理模型是位移的合成.平行四边形法则的物理模型是力的合成.
(3)应用:①两个非零向量的和;②为学习向量的其他运算奠定基础.
【思考】
向量加法的三角形法则和平行四边形法则的使用条件有什么不同?两者有何联
系?
3.
|a+b|,|a|,|b|之间的关系
一般地,我们有,当且仅当________________时等号成立.
4.向量加法的运算律
交换律
结合律
5.向量的减法
(1)本质:向量的减法是向量加法的逆运算.
(2)定义:若,则向量叫作与的差,记为.求两个向量差的运算,叫作
向量的减法.
(3)应用:①求两个向量的差;②为向量的综合运算奠定基础.
6.向量减法的几何意义
作法
已知向量,在平面内任取一点O,作,则
图示
(1)已知是不共线的向量,如何在同一个平行四边形中作出和?
(2)在代数运算中的移项法则,在向量中是否仍然成立?
【课前基础演练】
题1.(多选)下列命题正确的是
(
)
A.
存在向量,使得是一个实数.
B.
在平行四边形ABCD中,.
C.
.
D.
相反向量不一定是平行向量,平行向量一定是相反向量.
题2.在平行四边形ABCD中,下列结论错误的是
(
)
A.
B.
C.
D.
题3.若表示“向东走8
km”,
表示“向北走8
km”,则________,的方向是________.
关键能力·合作学习
类型一
三角形法则、平行四边形法则的应用(直观想象)
【题组训练】
题4.下列等式错误的是
(
)
A.
B.
C.
D.在?ABCD中,
题5.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则
(
)
A.
B.
C.
D.
题6.如图,已知向量.
(1)用平行四边形法则作出向量;
(2)用三角形法则作出向量.
【补偿训练】
题7.向量等于
(
)
A.
B.
C.
D.
题8.如图,已知?ABCD,O是两条对角线的交点,E是CD的一个三等分点,求作:
(1)
;
(2)
.
题9.已知,则___________.
【补偿训练】题10.如图,已知三个向量,试用三角形法则和平行四边形法则分别作向量.
类型二
向量减法的几何意义(直观想象)
【典例】题11.如图,已知向量不共线,求作向量.
【变式探究】
题12.如图,已知向量不共线,求作向量:
.
【跟踪训练】
题13.如图所示,O为△ABC内一点,
,求作:
.
【补偿训练】
题14.如图,已知向量,求作.
类型三
向量加减法的运算(数学运算)
【典例】题15.化简:
(1)
;
(2)
.
2.化简:(1)
;
(2)
;
(3)
;
(4)
;
(5)
;
(6)
.
【跟踪训练】
题16.设E是平行四边形ABCD外一点,如图所示,化简下列各式:
(1)________;
(2)________;
(3)________;
(4)________.
【补偿训练】
题17.在平行四边形ABCD中(如图),对角线AC,BD交于点O,则
①________.
②________.
③________.
④________.
题18.化简下列各式:(1);
(2).
【补偿训练】
题19.下列各式中不能化简为的是
(
)
A.
B.
C.
D.
类型四
向量加减法的综合应用(逻辑推理、数学运算)
角度1
与平面几何知识综合应用
【典例】题20.已知四边形ABCD的对角线AC与BD相交于点O,且.
求证:四边形ABCD是平行四边形.
【变式探究】
题21.四边形ABCD中,,且,求证四边形ABCD为矩形.
角度2
与物理知识综合
【典例】题22.一艘船以5
km/h的速度向垂直于对岸方向行驶,航船实际航行方向与
水流方向成30°角,求水流速度和船实际速度.
【思路导引】画出示意图,根据向量加法的几何意义分析水流速度、船垂直于对岸的方向行驶的速度和船实际航行的速度之间的关系,解直角三角形求有关线段和角的大小.
【题组训练】
题23.已知点G是△ABC的重心,则________.
题24.一架直升飞机从A地沿北偏东60°方向飞行了40
km到B地,再由B地沿正北方
向飞行40
km到达C地,求此时直升飞机与A地的相对位置.
【补偿训练】
题25.如图所示,P,Q是△ABC的边BC上两点,且.求证:.
题26.如图所示,在正八边形ABCDEFGH中,,
(1)试用已知向量表示;
(2)试用已知向量表示.
课堂检测·素养达标
题27.若C是线段AB的中点,则等于
(
)
A.
B.
C.
D.以上均不正确
题28.下列运算中正确的是
(
)
A.
B.
C.
D.
题29.化简:(1)________;
(2)________.
题30.根据下图填空:
.
题31.河水从东向西流,流速为2
m/s,一小船以2
m/s垂直水流方向向北横渡,求小
船实际航行的方向和航速(结果保留小数点后一位).
编号:002
课题:§9.2.1
向量的加减法
目标要求
1、理解并掌握向量的概念.
2、理解并掌握零向量与单位向量.
3、理解并掌握相等向量与共线向量.
4、理解并掌握向量的应用.
学科素养目标
向量注重“形”,是几何学的基础,广泛应用于实际生活和生产中.通过数形结合,了解向量知识在高中阶段的作用.
重点难点
重点:相等向量与共线向量;
难点:向量的应用.
教学过程
基础知识点
1.向量加法的定义
求___两个向量和__的运算,叫作向量的加法.
2.求向量和的方法
(1)三角形法则与平行四边形法则
三角
形法
则
作法
已知向量和,在平面内任取一点O,
作,则向量叫作与
的和,记作,即.
图示
平行
四边
形法
则
作法
对于任意两个不共线的非零向量,分别
作,以OA,OC为邻边作?OABC,则
以O为起点的对角线表示的向量就是向量与的和.
图示
规定
(2)本质:向量加法运算结果仍是向量,此向量的方向和大小可以用三角形法则和平行四边形法则作出.三角形法则的物理模型是位移的合成.平行四边形法则的物理模型是力的合成.
(3)应用:①两个非零向量的和;②为学习向量的其他运算奠定基础.
【思考】
向量加法的三角形法则和平行四边形法则的使用条件有什么不同?两者有何联
系?
提示:(1)三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于
两个不共线的向量求和.
(2)当两个向量不共线时,两个法则是一致的.
如图所示,(平行四边形法则),
又因为,
所以(三角形法则).
3.
|a+b|,|a|,|b|之间的关系
一般地,我们有,当且仅当__方向相同__时等号成立.
4.向量加法的运算律
交换律
结合律
5.向量的减法
(1)本质:向量的减法是向量加法的逆运算.
(2)定义:若,则向量叫作与的差,记为.求两个向量差的运算,叫作
向量的减法.
(3)应用:①求两个向量的差;②为向量的综合运算奠定基础.
6.向量减法的几何意义
作法
已知向量,在平面内任取一点O,作,则
图示
(1)已知是不共线的向量,如何在同一个平行四边形中作出和?
提示:如图所示,作平行四边形OACB,设,
根据向量加法的平行四边形法则和向量减法的三角形法则,有.
(2)在代数运算中的移项法则,在向量中是否仍然成立?
提示:成立.在向量等式的两边都加上或减去同一个向量仍得到向量等式,因此移项法则对向量等式也是适用的.
【课前基础演练】
题1.(多选)下列命题正确的是
(
)
A.
存在向量,使得是一个实数.
B.
在平行四边形ABCD中,.
C.
.
D.
相反向量不一定是平行向量,平行向量一定是相反向量.
【答案】选BC
提示:A×.两个向量的和仍是一个向量.
B√.由向量加法的平行四边形法则可知.
C√.由向量加法的交换律、结合律知,a+(b+c)=(a+b)+c=c+(a+b).
D×.由平行向量与相反向量的定义可知,相反向量必为平行向量,平行向量
不一定是相反向量.
故选BC.
题2.在平行四边形ABCD中,下列结论错误的是
(
)
A.
B.
C.
D.
【解析】选C.因为四边形ABCD是平行四边形,
所以,所以,A正确;
,由向量加法的平行四边形法则可知,,B正确;
,C错误;
因为四边形ABCD是平行四边形,所以与互为相反向量,所以,
D正确.
题3.若表示“向东走8
km”,
表示“向北走8
km”,则________,的方向是________.
【解析】如图所示,作,
则.
所以(km),
因为∠AOB=45°,
所以的方向是东北方向.
答案:
km
东北方向
关键能力·合作学习
类型一
三角形法则、平行四边形法则的应用(直观想象)
【题组训练】
题4.下列等式错误的是
(
)
A.
B.
C.
D.在?ABCD中,
【解析】选A.由向量加法可知.
题5.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则
(
)
A.
B.
C.
D.
【解析】选C.设,利用平行四边形法则作出向量,再平移即发现.
题6.如图,已知向量.
(1)用平行四边形法则作出向量;
(2)用三角形法则作出向量.
【解析】(1)如图,在平面内任取一点O,作,以OA,OB为邻边作?OACB,连接OC,则.
(2)如图,在平面内任取一点O',作,连接O'E,则.
【解题策略】
1.应用三角形法则应注意的问题
使用三角形法则求两个向量的和时,应注意“首尾相连,起点指终点”,即首尾
相连的两个向量的和对应的向量是第一个向量的起点指向第二个向量的终点.
2.应用平行四边形法则应注意的问题
(1)平行四边形法则只适用于求不共线的两个向量的和.
(2)基本步骤可简述为:共起点两向量所在线段为邻边作平行四边形,找共起点
的对角线对应的向量.
【补偿训练】
题7.向量等于
(
)
A.
B.
C.
D.
【解析】选C.
.
题8.如图,已知?ABCD,O是两条对角线的交点,E是CD的一个三等分点,求作:
(1)
;
(2)
.
【解析】(1)延长AC,在延长线上截取CF=AO,则向量即为所求.
(2)在AB上取点G,使AG=AB,则向量即为所求.
【拓展延伸】向量加法的多边形法则
向量加法的三角形法则可以推广为多个向量求和的多边形法则,即把每个向量
平移,使这些向量首尾相连,则由第一个向量的起点指向最后一个向量终点的向
量就是这些向量的和向量.
即:.或.
这是一个极其简单却非常有用的结论(如图).
利用向量加法的多边形法则化简多个向量的和有时非常有效.
【拓展训练】
题9.已知,则___________.
【解析】.
答案:
【补偿训练】题10.如图,已知三个向量,试用三角形法则和平行四边形法则分别作向量.
【解析】利用三角形法则作a+b+c,如图①所示,作,以A为起点,作,
再以B为起点,作,则.利用平行四边形法则作,如图②所示,作,以为邻边作?OADB,则,再以为邻边作?ODEC,则.
类型二
向量减法的几何意义(直观想象)
【典例】题11.如图,已知向量不共线,求作向量.
【思路导引】先作,再作.作向量的差时,可以依据定义也可以依据向量减法的三角形法则.
【解析】方法一:如图所示,在平面内任取一点O,作,则,再作,则.
方法二:如图所示,在平面内任取一点O,作,则,
再作,连接OC,则.
【变式探究】
题12.如图,已知向量不共线,求作向量:
.
【解析】如图所示:
【解题策略】
作两个向量的差的两种方法
(1)用向量减法的三角形法则
①步骤
②口诀:共起点,连终点,指向被减.
(2)用向量减法的定义
根据转化为向量加法运算,再作图.
【跟踪训练】
题13.如图所示,O为△ABC内一点,
,求作:
.
【解析】方法一:以为邻边作平行四边形OBDC,连接OD,AD,则.
方法二:作,连接AD,则.
【补偿训练】
题14.如图,已知向量,求作.
【解析】如图,以A为起点分别作向量和,使.连接CB,得向
量,再以C为起点作向量,使.连接DB,得向量.则向量即为所
求作的向量.
类型三
向量加减法的运算(数学运算)
【典例】题15.化简:
(1)
;
(2)
.
【解析】(1)
.
(2)
.
2.化简:(1)
;
(2)
;
(3)
;
(4)
;
(5)
;
(6)
.
【思路导引】1.综合利用向量加法的运算律和三角形法则解答.
2.首先用向量加法的运算律或向量减法的定义进行恰当转化,然后用向量加法(或减法)的三角形法则化简.
【解析】(1);
(2);
(3);
(4);
(5);
(6)方法一:.
方法二:
.
【解题策略】
1.向量与非零向量的模及方向的联系
(1)当向量与不共线时,向量的方向与都不相同,且,几何意义是三角形两边之和大于第三边.
(2)当向量与同向时,向量,方向相同,且.
(3)当向量与反向时,若时,则的方向与相同,且;
若时,则;若时,则\的方向与相同,且.
2.向量加法运算律的意义和应用原则
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现恰当利用向量
加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向
量的加法运算可以按照任意的次序、任意的组合来进行.
(2)应用原则:利用代数方法通过向量加法的交换律,使各向量“首尾相连”,
通过向量加法的结合律调整向量相加的顺序.
3.向量减法运算的常用方法
(1)可以通过相反向量,把向量减法的运算转化为加法运算.
(2)运用向量减法的三角形法则,此时要注意两个向量要有共同的起点.
(3)引入点O,逆用向量减法的三角形法则,将各向量起点统一.
【跟踪训练】
题16.设E是平行四边形ABCD外一点,如图所示,化简下列各式:
(1)________;
(2)________;
(3)________;
(4)________.
答案:(1);
(2);
(3);
(4)
【补偿训练】
题17.在平行四边形ABCD中(如图),对角线AC,BD交于点O,则
①________.
②________.
③________.
④________.
【解析】①
.
②.
③.
④.
答案:①;
②;
③;
④
题18.化简下列各式:(1);
(2).
【解析】(1).
(2).
【补偿训练】
题19.下列各式中不能化简为的是
(
)
A.
B.
C.
D.
【解析】选D.选项A中,;选项B
中,;选项C中,
.选项D中,
.
类型四
向量加减法的综合应用(逻辑推理、数学运算)
角度1
与平面几何知识综合应用
【典例】题20.已知四边形ABCD的对角线AC与BD相交于点O,且.
求证:四边形ABCD是平行四边形.
【思路导引】利用向量加法结合题目条件推证.
【证明】如图,,
又因为,所以.所以AB=DC且AB∥DC.所以四边形ABCD
为平行四边形.
【变式探究】
题21.四边形ABCD中,,且,求证四边形ABCD为矩形.
【证明】因为四边形ABCD中,,
所以四边形ABCD为平行四边形,如图.
所以,
因为,所以,
即平行四边形对角线相等,故四边形ABCD为矩形.
角度2
与物理知识综合
【典例】题22.一艘船以5
km/h的速度向垂直于对岸方向行驶,航船实际航行方向与
水流方向成30°角,求水流速度和船实际速度.
【思路导引】画出示意图,根据向量加法的几何意义分析水流速度、船垂直于对岸的方向行驶的速度和船实际航行的速度之间的关系,解直角三角形求有关线段和角的大小.
【解析】如图所示,表示水流速度,表示船垂直于对岸的方向行驶的速度,表示船实际航行的速度,∠AOC=30°,.
因为四边形OACB为矩形,所以.
所以水流速度大小为km/h,船实际速度为10
km/h.
【解题策略】
1.利用向量解决几何问题的方法
用向量法证明几何问题的关键是把几何中的线段转化为向量,通过向量的运算得到结论,然后把向量问题还原为几何问题.
2.利用向量的加法解决实际应用题的三个步骤
【题组训练】
题23.已知点G是△ABC的重心,则________.
【解析】如图所示,连接AG并延长交BC于E点,点E为BC的中点,延长AE到D点,使
GE=ED,则,所以.
答案:
题24.一架直升飞机从A地沿北偏东60°方向飞行了40
km到B地,再由B地沿正北方
向飞行40
km到达C地,求此时直升飞机与A地的相对位置.
【解析】如图所示,设分别是直升飞机两次位移,则表示两次位移的合位移,即.在Rt△ABD中,20
km,
km,在Rt△ACD中,,即此时直升飞机位于A地北偏东30°,且距离A地
km处.
【补偿训练】
题25.如图所示,P,Q是△ABC的边BC上两点,且.求证:.
【证明】因为,
所以.
又因为,所以.
题26.如图所示,在正八边形ABCDEFGH中,,
(1)试用已知向量表示;
(2)试用已知向量表示.
【解析】(1)由题图可知;
(2)由题图可知,.
课堂检测·素养达标
题27.若C是线段AB的中点,则等于
(
)
A.
B.
C.
D.以上均不正确
【解析】选C.与模相等而方向相反,因此.
题28.下列运算中正确的是
(
)
A.
B.
C.
D.
【解析】选C.根据向量减法的几何意义,知,所以C正确,A错误;B
显然错误;对于D,应该等于,而不是0.
题29.化简:(1)________;
(2)________.
【解析】(1)原式=.
(2)原式=.
答案:(1)
(2)
题30.根据下图填空:
.
【解析】根据向量加法的运算法则可知
.
答案:
题31.河水从东向西流,流速为2
m/s,一小船以2
m/s垂直水流方向向北横渡,求小
船实际航行的方向和航速(结果保留小数点后一位).
【解析】如图,表示船速,表示河水速度,以AB,AD为邻边作?ABCD,则表示小船实际航行的速度,在Rt△ABC中,,
于是≈2.8(m/s)
由,可得的方向为西北方向.
所以小船实际航行速度为向西北方向,2.8
m/s.
课题:§9.2.1
向量的加减法
目标要求
1、理解并掌握向量的概念.
2、理解并掌握零向量与单位向量.
3、理解并掌握相等向量与共线向量.
4、理解并掌握向量的应用.
学科素养目标
向量注重“形”,是几何学的基础,广泛应用于实际生活和生产中.通过数形结合,了解向量知识在高中阶段的作用.
重点难点
重点:相等向量与共线向量;
难点:向量的应用.
教学过程
基础知识点
1.向量加法的定义
求____________________的运算,叫作向量的加法.
2.求向量和的方法
(1)三角形法则与平行四边形法则
三角
形法
则
作法
已知向量和,在平面内任取一点O,
作,则向量叫作与
的和,记作,即.
图示
平行
四边
形法
则
作法
对于任意两个不共线的非零向量,分别
作,以OA,OC为邻边作?OABC,则
以O为起点的对角线表示的向量就是向量与的和.
图示
规定
(2)本质:向量加法运算结果仍是向量,此向量的方向和大小可以用三角形法则和平行四边形法则作出.三角形法则的物理模型是位移的合成.平行四边形法则的物理模型是力的合成.
(3)应用:①两个非零向量的和;②为学习向量的其他运算奠定基础.
【思考】
向量加法的三角形法则和平行四边形法则的使用条件有什么不同?两者有何联
系?
3.
|a+b|,|a|,|b|之间的关系
一般地,我们有,当且仅当________________时等号成立.
4.向量加法的运算律
交换律
结合律
5.向量的减法
(1)本质:向量的减法是向量加法的逆运算.
(2)定义:若,则向量叫作与的差,记为.求两个向量差的运算,叫作
向量的减法.
(3)应用:①求两个向量的差;②为向量的综合运算奠定基础.
6.向量减法的几何意义
作法
已知向量,在平面内任取一点O,作,则
图示
(1)已知是不共线的向量,如何在同一个平行四边形中作出和?
(2)在代数运算中的移项法则,在向量中是否仍然成立?
【课前基础演练】
题1.(多选)下列命题正确的是
(
)
A.
存在向量,使得是一个实数.
B.
在平行四边形ABCD中,.
C.
.
D.
相反向量不一定是平行向量,平行向量一定是相反向量.
题2.在平行四边形ABCD中,下列结论错误的是
(
)
A.
B.
C.
D.
题3.若表示“向东走8
km”,
表示“向北走8
km”,则________,的方向是________.
关键能力·合作学习
类型一
三角形法则、平行四边形法则的应用(直观想象)
【题组训练】
题4.下列等式错误的是
(
)
A.
B.
C.
D.在?ABCD中,
题5.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则
(
)
A.
B.
C.
D.
题6.如图,已知向量.
(1)用平行四边形法则作出向量;
(2)用三角形法则作出向量.
【补偿训练】
题7.向量等于
(
)
A.
B.
C.
D.
题8.如图,已知?ABCD,O是两条对角线的交点,E是CD的一个三等分点,求作:
(1)
;
(2)
.
题9.已知,则___________.
【补偿训练】题10.如图,已知三个向量,试用三角形法则和平行四边形法则分别作向量.
类型二
向量减法的几何意义(直观想象)
【典例】题11.如图,已知向量不共线,求作向量.
【变式探究】
题12.如图,已知向量不共线,求作向量:
.
【跟踪训练】
题13.如图所示,O为△ABC内一点,
,求作:
.
【补偿训练】
题14.如图,已知向量,求作.
类型三
向量加减法的运算(数学运算)
【典例】题15.化简:
(1)
;
(2)
.
2.化简:(1)
;
(2)
;
(3)
;
(4)
;
(5)
;
(6)
.
【跟踪训练】
题16.设E是平行四边形ABCD外一点,如图所示,化简下列各式:
(1)________;
(2)________;
(3)________;
(4)________.
【补偿训练】
题17.在平行四边形ABCD中(如图),对角线AC,BD交于点O,则
①________.
②________.
③________.
④________.
题18.化简下列各式:(1);
(2).
【补偿训练】
题19.下列各式中不能化简为的是
(
)
A.
B.
C.
D.
类型四
向量加减法的综合应用(逻辑推理、数学运算)
角度1
与平面几何知识综合应用
【典例】题20.已知四边形ABCD的对角线AC与BD相交于点O,且.
求证:四边形ABCD是平行四边形.
【变式探究】
题21.四边形ABCD中,,且,求证四边形ABCD为矩形.
角度2
与物理知识综合
【典例】题22.一艘船以5
km/h的速度向垂直于对岸方向行驶,航船实际航行方向与
水流方向成30°角,求水流速度和船实际速度.
【思路导引】画出示意图,根据向量加法的几何意义分析水流速度、船垂直于对岸的方向行驶的速度和船实际航行的速度之间的关系,解直角三角形求有关线段和角的大小.
【题组训练】
题23.已知点G是△ABC的重心,则________.
题24.一架直升飞机从A地沿北偏东60°方向飞行了40
km到B地,再由B地沿正北方
向飞行40
km到达C地,求此时直升飞机与A地的相对位置.
【补偿训练】
题25.如图所示,P,Q是△ABC的边BC上两点,且.求证:.
题26.如图所示,在正八边形ABCDEFGH中,,
(1)试用已知向量表示;
(2)试用已知向量表示.
课堂检测·素养达标
题27.若C是线段AB的中点,则等于
(
)
A.
B.
C.
D.以上均不正确
题28.下列运算中正确的是
(
)
A.
B.
C.
D.
题29.化简:(1)________;
(2)________.
题30.根据下图填空:
.
题31.河水从东向西流,流速为2
m/s,一小船以2
m/s垂直水流方向向北横渡,求小
船实际航行的方向和航速(结果保留小数点后一位).
编号:002
课题:§9.2.1
向量的加减法
目标要求
1、理解并掌握向量的概念.
2、理解并掌握零向量与单位向量.
3、理解并掌握相等向量与共线向量.
4、理解并掌握向量的应用.
学科素养目标
向量注重“形”,是几何学的基础,广泛应用于实际生活和生产中.通过数形结合,了解向量知识在高中阶段的作用.
重点难点
重点:相等向量与共线向量;
难点:向量的应用.
教学过程
基础知识点
1.向量加法的定义
求___两个向量和__的运算,叫作向量的加法.
2.求向量和的方法
(1)三角形法则与平行四边形法则
三角
形法
则
作法
已知向量和,在平面内任取一点O,
作,则向量叫作与
的和,记作,即.
图示
平行
四边
形法
则
作法
对于任意两个不共线的非零向量,分别
作,以OA,OC为邻边作?OABC,则
以O为起点的对角线表示的向量就是向量与的和.
图示
规定
(2)本质:向量加法运算结果仍是向量,此向量的方向和大小可以用三角形法则和平行四边形法则作出.三角形法则的物理模型是位移的合成.平行四边形法则的物理模型是力的合成.
(3)应用:①两个非零向量的和;②为学习向量的其他运算奠定基础.
【思考】
向量加法的三角形法则和平行四边形法则的使用条件有什么不同?两者有何联
系?
提示:(1)三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于
两个不共线的向量求和.
(2)当两个向量不共线时,两个法则是一致的.
如图所示,(平行四边形法则),
又因为,
所以(三角形法则).
3.
|a+b|,|a|,|b|之间的关系
一般地,我们有,当且仅当__方向相同__时等号成立.
4.向量加法的运算律
交换律
结合律
5.向量的减法
(1)本质:向量的减法是向量加法的逆运算.
(2)定义:若,则向量叫作与的差,记为.求两个向量差的运算,叫作
向量的减法.
(3)应用:①求两个向量的差;②为向量的综合运算奠定基础.
6.向量减法的几何意义
作法
已知向量,在平面内任取一点O,作,则
图示
(1)已知是不共线的向量,如何在同一个平行四边形中作出和?
提示:如图所示,作平行四边形OACB,设,
根据向量加法的平行四边形法则和向量减法的三角形法则,有.
(2)在代数运算中的移项法则,在向量中是否仍然成立?
提示:成立.在向量等式的两边都加上或减去同一个向量仍得到向量等式,因此移项法则对向量等式也是适用的.
【课前基础演练】
题1.(多选)下列命题正确的是
(
)
A.
存在向量,使得是一个实数.
B.
在平行四边形ABCD中,.
C.
.
D.
相反向量不一定是平行向量,平行向量一定是相反向量.
【答案】选BC
提示:A×.两个向量的和仍是一个向量.
B√.由向量加法的平行四边形法则可知.
C√.由向量加法的交换律、结合律知,a+(b+c)=(a+b)+c=c+(a+b).
D×.由平行向量与相反向量的定义可知,相反向量必为平行向量,平行向量
不一定是相反向量.
故选BC.
题2.在平行四边形ABCD中,下列结论错误的是
(
)
A.
B.
C.
D.
【解析】选C.因为四边形ABCD是平行四边形,
所以,所以,A正确;
,由向量加法的平行四边形法则可知,,B正确;
,C错误;
因为四边形ABCD是平行四边形,所以与互为相反向量,所以,
D正确.
题3.若表示“向东走8
km”,
表示“向北走8
km”,则________,的方向是________.
【解析】如图所示,作,
则.
所以(km),
因为∠AOB=45°,
所以的方向是东北方向.
答案:
km
东北方向
关键能力·合作学习
类型一
三角形法则、平行四边形法则的应用(直观想象)
【题组训练】
题4.下列等式错误的是
(
)
A.
B.
C.
D.在?ABCD中,
【解析】选A.由向量加法可知.
题5.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则
(
)
A.
B.
C.
D.
【解析】选C.设,利用平行四边形法则作出向量,再平移即发现.
题6.如图,已知向量.
(1)用平行四边形法则作出向量;
(2)用三角形法则作出向量.
【解析】(1)如图,在平面内任取一点O,作,以OA,OB为邻边作?OACB,连接OC,则.
(2)如图,在平面内任取一点O',作,连接O'E,则.
【解题策略】
1.应用三角形法则应注意的问题
使用三角形法则求两个向量的和时,应注意“首尾相连,起点指终点”,即首尾
相连的两个向量的和对应的向量是第一个向量的起点指向第二个向量的终点.
2.应用平行四边形法则应注意的问题
(1)平行四边形法则只适用于求不共线的两个向量的和.
(2)基本步骤可简述为:共起点两向量所在线段为邻边作平行四边形,找共起点
的对角线对应的向量.
【补偿训练】
题7.向量等于
(
)
A.
B.
C.
D.
【解析】选C.
.
题8.如图,已知?ABCD,O是两条对角线的交点,E是CD的一个三等分点,求作:
(1)
;
(2)
.
【解析】(1)延长AC,在延长线上截取CF=AO,则向量即为所求.
(2)在AB上取点G,使AG=AB,则向量即为所求.
【拓展延伸】向量加法的多边形法则
向量加法的三角形法则可以推广为多个向量求和的多边形法则,即把每个向量
平移,使这些向量首尾相连,则由第一个向量的起点指向最后一个向量终点的向
量就是这些向量的和向量.
即:.或.
这是一个极其简单却非常有用的结论(如图).
利用向量加法的多边形法则化简多个向量的和有时非常有效.
【拓展训练】
题9.已知,则___________.
【解析】.
答案:
【补偿训练】题10.如图,已知三个向量,试用三角形法则和平行四边形法则分别作向量.
【解析】利用三角形法则作a+b+c,如图①所示,作,以A为起点,作,
再以B为起点,作,则.利用平行四边形法则作,如图②所示,作,以为邻边作?OADB,则,再以为邻边作?ODEC,则.
类型二
向量减法的几何意义(直观想象)
【典例】题11.如图,已知向量不共线,求作向量.
【思路导引】先作,再作.作向量的差时,可以依据定义也可以依据向量减法的三角形法则.
【解析】方法一:如图所示,在平面内任取一点O,作,则,再作,则.
方法二:如图所示,在平面内任取一点O,作,则,
再作,连接OC,则.
【变式探究】
题12.如图,已知向量不共线,求作向量:
.
【解析】如图所示:
【解题策略】
作两个向量的差的两种方法
(1)用向量减法的三角形法则
①步骤
②口诀:共起点,连终点,指向被减.
(2)用向量减法的定义
根据转化为向量加法运算,再作图.
【跟踪训练】
题13.如图所示,O为△ABC内一点,
,求作:
.
【解析】方法一:以为邻边作平行四边形OBDC,连接OD,AD,则.
方法二:作,连接AD,则.
【补偿训练】
题14.如图,已知向量,求作.
【解析】如图,以A为起点分别作向量和,使.连接CB,得向
量,再以C为起点作向量,使.连接DB,得向量.则向量即为所
求作的向量.
类型三
向量加减法的运算(数学运算)
【典例】题15.化简:
(1)
;
(2)
.
【解析】(1)
.
(2)
.
2.化简:(1)
;
(2)
;
(3)
;
(4)
;
(5)
;
(6)
.
【思路导引】1.综合利用向量加法的运算律和三角形法则解答.
2.首先用向量加法的运算律或向量减法的定义进行恰当转化,然后用向量加法(或减法)的三角形法则化简.
【解析】(1);
(2);
(3);
(4);
(5);
(6)方法一:.
方法二:
.
【解题策略】
1.向量与非零向量的模及方向的联系
(1)当向量与不共线时,向量的方向与都不相同,且,几何意义是三角形两边之和大于第三边.
(2)当向量与同向时,向量,方向相同,且.
(3)当向量与反向时,若时,则的方向与相同,且;
若时,则;若时,则\的方向与相同,且.
2.向量加法运算律的意义和应用原则
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现恰当利用向量
加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向
量的加法运算可以按照任意的次序、任意的组合来进行.
(2)应用原则:利用代数方法通过向量加法的交换律,使各向量“首尾相连”,
通过向量加法的结合律调整向量相加的顺序.
3.向量减法运算的常用方法
(1)可以通过相反向量,把向量减法的运算转化为加法运算.
(2)运用向量减法的三角形法则,此时要注意两个向量要有共同的起点.
(3)引入点O,逆用向量减法的三角形法则,将各向量起点统一.
【跟踪训练】
题16.设E是平行四边形ABCD外一点,如图所示,化简下列各式:
(1)________;
(2)________;
(3)________;
(4)________.
答案:(1);
(2);
(3);
(4)
【补偿训练】
题17.在平行四边形ABCD中(如图),对角线AC,BD交于点O,则
①________.
②________.
③________.
④________.
【解析】①
.
②.
③.
④.
答案:①;
②;
③;
④
题18.化简下列各式:(1);
(2).
【解析】(1).
(2).
【补偿训练】
题19.下列各式中不能化简为的是
(
)
A.
B.
C.
D.
【解析】选D.选项A中,;选项B
中,;选项C中,
.选项D中,
.
类型四
向量加减法的综合应用(逻辑推理、数学运算)
角度1
与平面几何知识综合应用
【典例】题20.已知四边形ABCD的对角线AC与BD相交于点O,且.
求证:四边形ABCD是平行四边形.
【思路导引】利用向量加法结合题目条件推证.
【证明】如图,,
又因为,所以.所以AB=DC且AB∥DC.所以四边形ABCD
为平行四边形.
【变式探究】
题21.四边形ABCD中,,且,求证四边形ABCD为矩形.
【证明】因为四边形ABCD中,,
所以四边形ABCD为平行四边形,如图.
所以,
因为,所以,
即平行四边形对角线相等,故四边形ABCD为矩形.
角度2
与物理知识综合
【典例】题22.一艘船以5
km/h的速度向垂直于对岸方向行驶,航船实际航行方向与
水流方向成30°角,求水流速度和船实际速度.
【思路导引】画出示意图,根据向量加法的几何意义分析水流速度、船垂直于对岸的方向行驶的速度和船实际航行的速度之间的关系,解直角三角形求有关线段和角的大小.
【解析】如图所示,表示水流速度,表示船垂直于对岸的方向行驶的速度,表示船实际航行的速度,∠AOC=30°,.
因为四边形OACB为矩形,所以.
所以水流速度大小为km/h,船实际速度为10
km/h.
【解题策略】
1.利用向量解决几何问题的方法
用向量法证明几何问题的关键是把几何中的线段转化为向量,通过向量的运算得到结论,然后把向量问题还原为几何问题.
2.利用向量的加法解决实际应用题的三个步骤
【题组训练】
题23.已知点G是△ABC的重心,则________.
【解析】如图所示,连接AG并延长交BC于E点,点E为BC的中点,延长AE到D点,使
GE=ED,则,所以.
答案:
题24.一架直升飞机从A地沿北偏东60°方向飞行了40
km到B地,再由B地沿正北方
向飞行40
km到达C地,求此时直升飞机与A地的相对位置.
【解析】如图所示,设分别是直升飞机两次位移,则表示两次位移的合位移,即.在Rt△ABD中,20
km,
km,在Rt△ACD中,,即此时直升飞机位于A地北偏东30°,且距离A地
km处.
【补偿训练】
题25.如图所示,P,Q是△ABC的边BC上两点,且.求证:.
【证明】因为,
所以.
又因为,所以.
题26.如图所示,在正八边形ABCDEFGH中,,
(1)试用已知向量表示;
(2)试用已知向量表示.
【解析】(1)由题图可知;
(2)由题图可知,.
课堂检测·素养达标
题27.若C是线段AB的中点,则等于
(
)
A.
B.
C.
D.以上均不正确
【解析】选C.与模相等而方向相反,因此.
题28.下列运算中正确的是
(
)
A.
B.
C.
D.
【解析】选C.根据向量减法的几何意义,知,所以C正确,A错误;B
显然错误;对于D,应该等于,而不是0.
题29.化简:(1)________;
(2)________.
【解析】(1)原式=.
(2)原式=.
答案:(1)
(2)
题30.根据下图填空:
.
【解析】根据向量加法的运算法则可知
.
答案:
题31.河水从东向西流,流速为2
m/s,一小船以2
m/s垂直水流方向向北横渡,求小
船实际航行的方向和航速(结果保留小数点后一位).
【解析】如图,表示船速,表示河水速度,以AB,AD为邻边作?ABCD,则表示小船实际航行的速度,在Rt△ABC中,,
于是≈2.8(m/s)
由,可得的方向为西北方向.
所以小船实际航行速度为向西北方向,2.8
m/s.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
