2020-2021学年苏科版八年级下册 第9章:中心对称图形——平行四边形 重难点题型训练试卷(二)(Word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级下册 第9章:中心对称图形——平行四边形 重难点题型训练试卷(二)(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 222.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 07:37:00 | ||
图片预览


文档简介
八年级下册
第9章:中心对称图形——平行四边形
重难点题型训练(二)
1.如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
(1)求证:BE=DF;
(2)线段OE满足什么条件时,四边形BEDF为矩形(不必证明).
2.如图所示△ABC中,∠C=90°,∠A,∠B的平分线交于D点,DE⊥BC于点E,DF⊥AC于点F.
(1)求证:四边形CEDF为正方形;
(2)若AC=6,BC=8,求CE的长.
3.如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE.与BF相交于O,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=6,CE=3,求ABCD的面积.
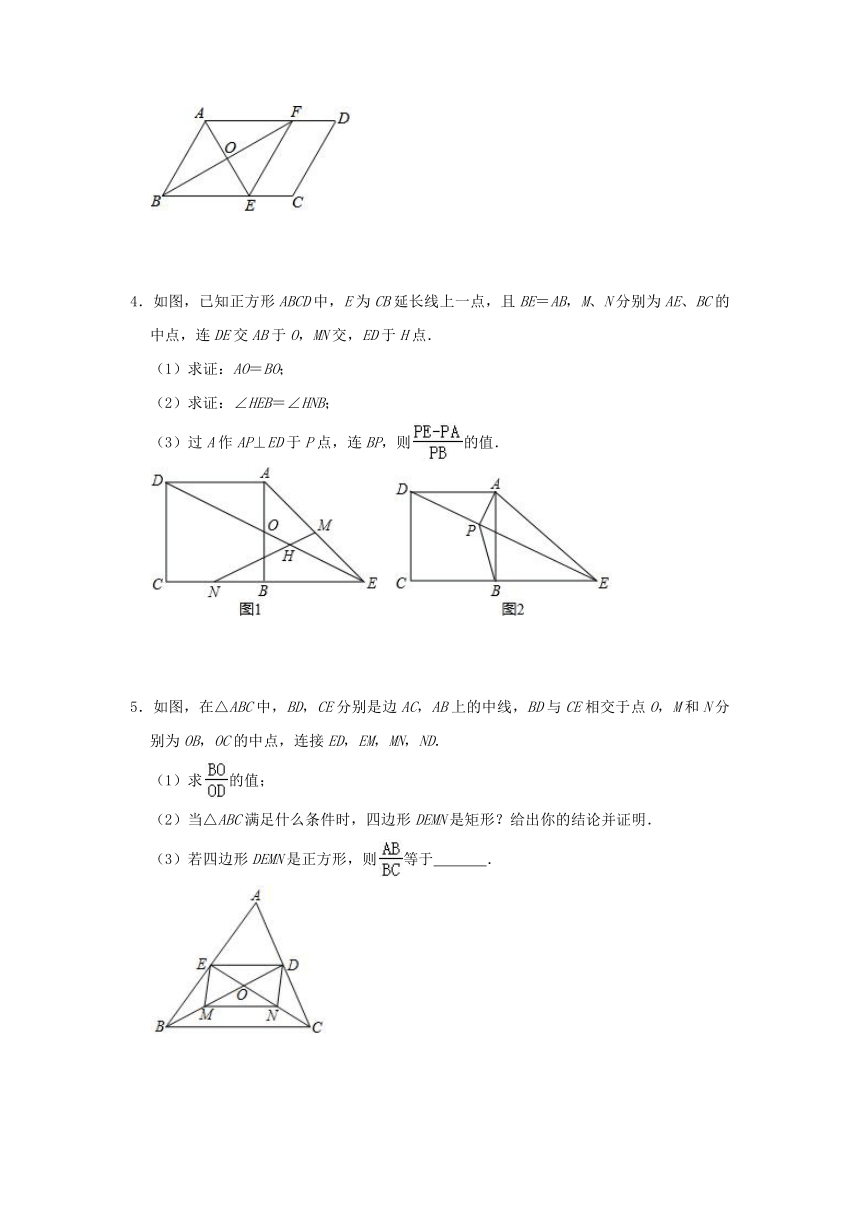
4.如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
5.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,M和N分别为OB,OC的中点,连接ED,EM,MN,ND.
(1)求的值;
(2)当△ABC满足什么条件时,四边形DEMN是矩形?给出你的结论并证明.
(3)若四边形DEMN是正方形,则等于
.
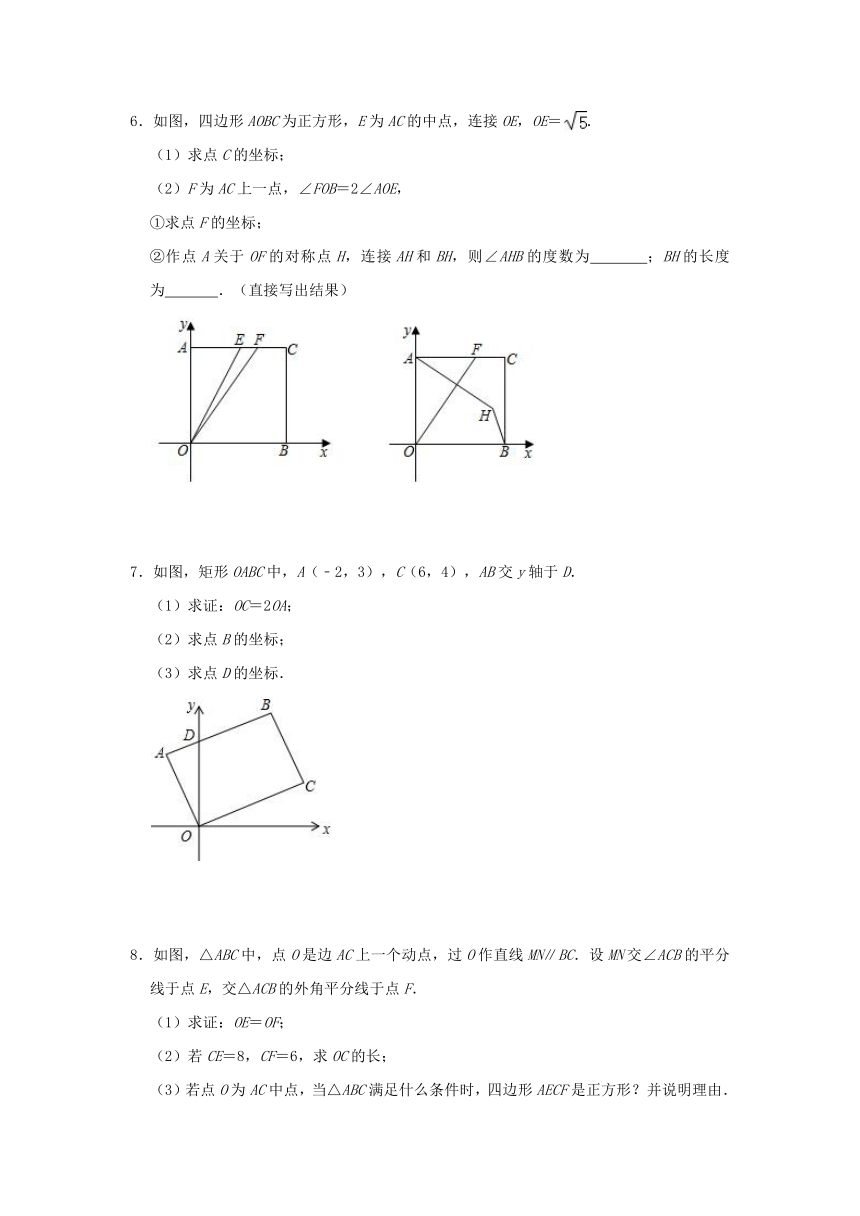
6.如图,四边形AOBC为正方形,E为AC的中点,连接OE,OE=.
(1)求点C的坐标;
(2)F为AC上一点,∠FOB=2∠AOE,
①求点F的坐标;
②作点A关于OF的对称点H,连接AH和BH,则∠AHB的度数为
;BH的长度为
.(直接写出结果)
7.如图,矩形OABC中,A(﹣2,3),C(6,4),AB交y轴于D.
(1)求证:OC=2OA;
(2)求点B的坐标;
(3)求点D的坐标.
8.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交△ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)若点O为AC中点,当△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
9.如图所示,在平行四边形ABCD中,CE交BA的延长线于F.
(1)若CE平分∠BCD,证明:BC=BF.
(2)若E为AD中点,证明:AF=AB.
10.如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.
(1)求证:DC=BE;
(2)若∠AEC=66°,求∠BCE的度数.
11.已知正方形ABCD中,点E和点G分别在边AD和BC上,连接AG交BE于点F,交BD于点K,若∠AKD=∠FBG.
(1)如图1,求证:∠BAG=∠EBD;
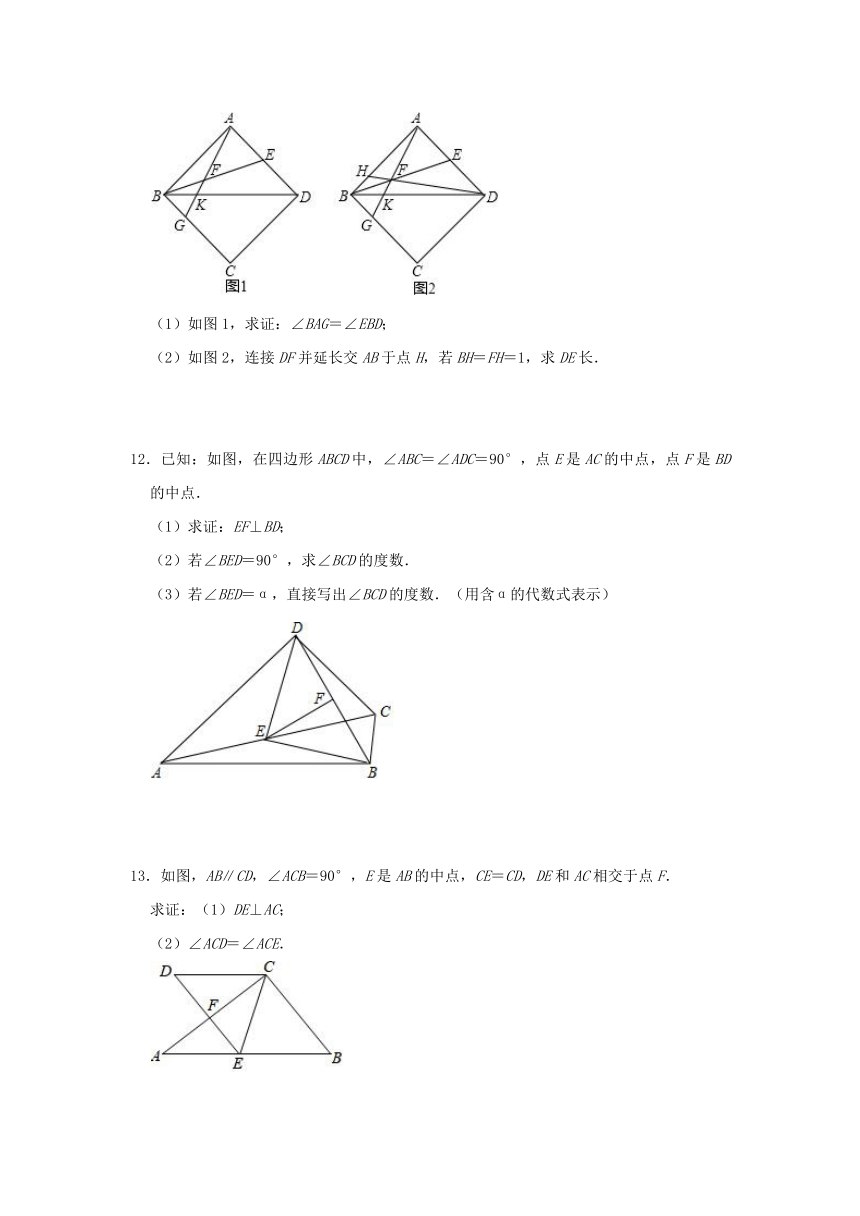
(2)如图2,连接DF并延长交AB于点H,若BH=FH=1,求DE长.
12.已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点,点F是BD的中点.
(1)求证:EF⊥BD;
(2)若∠BED=90°,求∠BCD的度数.
(3)若∠BED=α,直接写出∠BCD的度数.(用含α的代数式表示)
13.如图,AB∥CD,∠ACB=90°,E是AB的中点,CE=CD,DE和AC相交于点F.
求证:(1)DE⊥AC;
(2)∠ACD=∠ACE.
14.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=5,BC=12,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=70°,求∠FME的度数.
15.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,
(1)求证:DE∥BC;
(2)若AB=6,AC=10,点P为线段BC上一点,求BP长为多少时△DEP为等腰三角形?
参考答案
1.(1)证明:连接BE、DF,
∵四边形ABCD是平行四边形,
∴DO=BO,
∵OE=OF,
∴四边形DEBF是平行四边形,
∴DF=BE;
(2)解:当OE=DO时,四边形BEDF为矩形.
2.(1)证明:过点D作DN⊥AB于点N,
∵∠C=90°,DE⊥BC于点E,DF⊥AC于点F,
∴四边形FCED是矩形,
又∵∠A,∠B的平分线交于D点,
∴DF=DE=DN,
∴矩形FCED是正方形;
(2)解:∵AC=6,BC=8,∠C=90°,
∴AB=10,
∵四边形CEDF为正方形,
∴DF=DE=DN,
∴DF×AC+DE×BC+DN×AB=AC×BC,
则EC(AC+BC+AB)=AC×BC,
故EC==2.
3.证明:(1)∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,
同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF.
∴四边形ABEF是菱形.
(2)作FG⊥BC于G,
∵四边形ABEF是菱形,AE=6,BF=6,
∴AE⊥BF,OE=AE=3,OB=BF=3,
∴BE=,
∵S菱形ABEF=?AE?BF=BE?FG,
∴GF=3,
∴S平行四边形ABCD=BC?FG=27.
4.(1)证明:∵四边形ABCD是正方形,
∴AD=AB,AD∥BC,
∴∠DAB=∠ABE,∠ADO=∠BCO,
∵AB=BE,
∴AD=BE,
∴△ADO≌△BEO(ASA),
∴AO=BO;
(2)证明:延长BC至F,且使CF=BE,连接AF、DF,如图1所示:
则BF=CE,
∵四边形ABCD是矩形,
∴AB=DC,AD∥BC,∠BAD=∠ABC=∠DCB=90°,
在△ABF和△DCE中,,
∴△ABF≌△DCE(SAS),
∴∠DEC=∠AFB,
∵EB=CF,BN=CN,
∴N为EF的中点,
∴MN为△AEF的中位线,
∴MN∥AF,
∴∠HNB=∠AFB=∠HEB;
(3)解:过点B作BQ⊥BP交DE于Q,如图2所示:
则∠PBQ=90°,
∵∠ABE=180°﹣∠ABC=90°,
∴∠EBQ=∠ABP,
∵AD∥BC,
∴∠ADP=∠BEQ,
∵AP⊥DE,∠BAD=90°,
由角的互余关系得:∠BAP=∠ADP,
∴∠BEQ=∠BAP,
在△BEQ和△BAP中,,
∴△BEQ≌△BAP(ASA),
∴PA=QE,QB=PB,
∴△PBQ是等腰直角三角形,
∴PQ=PB,
∴==.
5.(1)解:∵D、E、M、N分别为AC、AB、OB、OC的中点,
∴DE∥BC,DE=BC,MN∥BC,MN=BC,
∴DE∥MN,DE=MN,
∴四边形EMND为平行四边形,
∴OM=OD,
∵OM=BM,
∴OB=2OM=2OD,
∴=2;
(2)当AB=AC时,四边形DEMN为矩形,
理由如下:∵D、E为AC、AB的中点,
∴AD=AC,AE=AB,
∴AD=AE,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(AAS),
∴BD=CE,
∵OD=OM=BM,
∴MD=BD,同理EN=EC,
∴MD=EN,
∴四边形DEMN为矩形;
(3)设DE=x,
∴BC=2x,
∵四边形DEMN是正方形,
∴OE=OD,OE⊥OD,
∴OE=OD=x,OB=x,
∴BE==x,
∴AB=x,
则==,
故答案为:.
6.解:(1)∵四边形AOBC为正方形,
∴OA=AC=CB=BO,∠OAC=∠ACB=∠CBO=∠BOA=90°,
∵E为AC的中点,
∴AE=EC=x,则AC=AO=2x,
在Rt△AOE中:,解得:x=1,
∴OA=AC=2,
∴C(2,2).
(2)①取BC中点M,延长OM交AC延长线于点N,
∵OA=OB,∠OAE=∠OBM,AE=BM,
∴△AOE≌△OBM(SAS),
∴∠AOE=∠BOM
又∵∠FOB=2∠AOE,
∴∠FOM=∠BOM=∠AOE,
又∵CN∥OB,
∴∠BOM=∠CNM,
∴∠FOM=∠FNO,
∴FO=FN,
∵BM=MC,∠MCN=∠MBO=90°,∠BOM=∠CNM,
∴△CMN≌△BMO(AAS),
∴CN=OB=2,
设CF=x,则AF=2﹣x,NF=2+x=FO,
在Rt△AOF中:AF2+AO2=OF2,
∴(2﹣x)2+22=(2+x)2,解得:x=0.5,
∴F(1.5,2).
②如图2,连接OH,AB,则AB=AC=2.
∵A与H关于AF对称,
∴∠AOF=∠HOF,OH=OA=OB,OF垂直平分AH,
作OP⊥BH于P,则∠BOP=∠HOP,
∵∠AOH+∠BOH=∠AOB=90°,
∴∠FOP=45°,
∵∠OQH=∠OPH=90°,
∴∠AHB=180°﹣∠FOP=135°,
∵F(1.5,2),
∴AF=1.5,
∴OF=2.5,
∴AH=2AQ===,
作BN⊥AH于N,则∠BHN=∠HBN=45°,
∴BN=HN=x,
∴BH=x,AN=AH+HN=+x,
在Rt△ANB中:AB2=AN2+BN2,
∴8=+x2,解得,(舍),
∴BH=.
7.解:(1)过A作AM⊥x轴于M,过C作CN⊥x轴于N,
∵A(﹣2,3),C(6,4),
∴AM=3ON=6,
∵矩形OABC中,∠AOC=90°,
∴∠MAO+∠AOM=∠AOM+∠CON=90°,
∴∠MAO=∠CON,
∴△AOM∽△OCN,
∴,
∴OC=2OA;
(2)过B作BH⊥x轴于H,过C作CE⊥BH于E,
则△AOM≌△BCE(AAS),
∴BE=AM=3,CE=OM=2,
∴BH=3+4=7,OH=6﹣2=4,
∴B(4,7);
(3)过A作AG⊥y轴于G,
∴OG=AM=3,
∵∠OAD=90°,
∴AO2=OG?OD,
∴AM2+OM2=13=3×OD,
∴OD=,
∴D(0,).
8.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,
∴∠ECF=∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF==10,
∴OC=EF=5;
(3)当△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
证明:∵O为AC中点,
∴OA=OC,
∵由(1)知OE=OF,
∴AO=EO=CO=FO,
∴?AECF为矩形,
又∵MN∥BC,∠ACB=90°,
∴∠AOE=∠ACB=90°,
∴AC⊥EF.
∴四边形AECF是正方形.
∴当△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
9.证明:(1)∵CE平分∠BCD,
∴∠ECD=∠FCB,
∵四边形ABCD是平行四边形,
∴∠FCD=∠BFC,
∴∠FCB=∠BFC,
∴BC=BF.
(2)∵E为AD中点,
∴DE=AE,
在△DEC与△AEF中,
∴△DEC≌△AEF(AAS),
∴AF=AB.
10.(1)证明:连接DE.
∵AD⊥BC,
∴∠ADB=90°,
∵AE=EB,
∴DE=EB=EA,
∵DG⊥EC,EG=GC,
∴DE=CD,
∴DC=BE.
(2)设∠BCE=x.
∵EB=DE=DC,
∴∠DCE=∠DEC=x,
∴∠EBD=∠BDE=∠DEC+∠DCE=2x,
∵∠AEC=∠EBD+∠ECD,
∴66°=3x,
∴x=22°,
∴∠BCE=22°.
11.(1)证明:如图1中,
∵四边形ABCD是正方形,
∴∠ABD=∠DBC=45°,
∵∠AKD=∠FBG,
∴∠ABD+∠BAG=∠DBC+∠EBD,
∴∠BAG=∠EBD.
(2)解:如图2中,作EP∥BD交AB于P,连接PF.AF交AF于O.
∵四边形ABCD是正方形,
∴∠ABD=∠ADB=45°,
∵EP∥BD,
∴∠APE=∠ABD,∠AEP=∠ADB,
∴∠APE=∠AEP=45°,
∴AP=AE,
∵AB=AD,
∴PB=DE,
∵∠OFE=∠ABF+∠BAF=∠ABF+∠EBD=45°,
∴∠APO=∠EFO,∵∠AOP=∠EOF,
∴△AOP∽△EOF,
∴=,
∴=,∵∠AOE=∠POF,
∴△AOE∽△POF,
∴∠PEO=∠AEO=45°,
∴∠PFE=∠BFP=90°,
∵BH=FH,
∴∠HBF=∠HFB,
∵∠HFB+∠BPF=90°,∠HFB+∠PFH=90°,
∴∠HPF=∠HFP,
∴FH=PH=BH=1,
∴PB=2,
∴DE=PB=2,
12.(1)证明:∵∠ABC=∠ADC=90°,点E是AC的中点,
∴DE=AC,BE=AC,
∴DE=BE,
∵点F是BD的中点,
∴EF⊥BD;
(2)解:∵∠ABC=∠ADC=90°,点E是AC的中点,
∴DE=AC=EC,BE=AC=EC,
∴∠EDC=∠DCE,∠EBC=∠ECB,
∵在四边形DEBC中,∠EDC+∠DCE+∠ECB+∠EBC+∠DEB=360°,
∵∠DEB=90°,
∵∠EDC+∠DCE+∠ECB+∠EBC=360°﹣∠DEB=360°﹣90°=270°,
∴2∠DCE+2∠ECB=270°,
∴∠DCE+∠ECB=135°,
即∠BCD=135°;
(3)若∠BED=α,则∠BCD=180°﹣,
理由是:∵∠ABC=∠ADC=90°,点E是AC的中点,
∴DE=AC=EC,BE=AC=EC,
∴∠EDC=∠DCE,∠EBC=∠ECB,
∵在四边形DEBC中,∠EDC+∠DCE+∠ECB+∠EBC+∠BED=360°,
∵∠BED=α,
∵∠EDC+∠DCE+∠ECB+∠EBC=360°﹣∠BED=360°﹣α,
∴2∠DCE+2∠ECB=360°﹣α,
∴∠DCE+∠ECB=180°﹣,
即∠BCD=180α.
13.证明:(1)直角三角形ACB中,
∵CE是斜边AB的中线,
∴CE=AE=BE=CD,
又∵AB∥CD,
∴BCDE为平行四边形,
∴BC∥DE,
∵AC⊥BC,
∴DE⊥AC.
(2)∵CD∥AB,
∴∠ACD=∠CAE.
由(1)知EC=EA,
∴∠A=∠ACE.
∴∠ACD=∠ACE.
14.解:(1)∵CF⊥AB于F,M为BC的中点,
∴ME=MC=BC=×12=6,
同理MF=MB=BC=×12=6,
∴△EFM的周长=6+6+5=17;
(2)∵MF=MB,
∴∠ABC=∠MFB=50°,
同理∠ACB=∠MEC=70°,
∴∠BMF=180°﹣50°﹣50°=80°,
∠EMC=180°﹣70°﹣70°=40°,
∴∠FME=180°﹣80°﹣40°=60°.
15.(1)证明:∵∠ABC=90°,点D是AC的中点,
∴BD=AD=AC,
∵DE是∠ADB的角平分线,
∴DE⊥AB,
又∵∠ABC=90°,
∴DE∥BC;
(2)解:由(1)知,DE∥BC,
又点D是AC的中点,
∴DE是△ABC的中位线,
∵AB=6,AC=10,
∴AE=3,AD=5,DE⊥AB,
∴DE===4,
∵DE⊥AB,AD=BD,
∴BE=AE=3,
①DE=EP时,BP==,
②DP=EP时,BP=DE=×4=2,
③DE=DP时,过点D作DF⊥BC于F,
则DF=BE=3,
由勾股定理得,FP==,
点P在F下边时,BP=4﹣,
点P在F上边时,BP=4+,
综上所述,BP的值为,2,4﹣,4+.
第9章:中心对称图形——平行四边形
重难点题型训练(二)
1.如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
(1)求证:BE=DF;
(2)线段OE满足什么条件时,四边形BEDF为矩形(不必证明).
2.如图所示△ABC中,∠C=90°,∠A,∠B的平分线交于D点,DE⊥BC于点E,DF⊥AC于点F.
(1)求证:四边形CEDF为正方形;
(2)若AC=6,BC=8,求CE的长.
3.如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE.与BF相交于O,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=6,CE=3,求ABCD的面积.
4.如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
5.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,M和N分别为OB,OC的中点,连接ED,EM,MN,ND.
(1)求的值;
(2)当△ABC满足什么条件时,四边形DEMN是矩形?给出你的结论并证明.
(3)若四边形DEMN是正方形,则等于
.
6.如图,四边形AOBC为正方形,E为AC的中点,连接OE,OE=.
(1)求点C的坐标;
(2)F为AC上一点,∠FOB=2∠AOE,
①求点F的坐标;
②作点A关于OF的对称点H,连接AH和BH,则∠AHB的度数为
;BH的长度为
.(直接写出结果)
7.如图,矩形OABC中,A(﹣2,3),C(6,4),AB交y轴于D.
(1)求证:OC=2OA;
(2)求点B的坐标;
(3)求点D的坐标.
8.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交△ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)若点O为AC中点,当△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
9.如图所示,在平行四边形ABCD中,CE交BA的延长线于F.
(1)若CE平分∠BCD,证明:BC=BF.
(2)若E为AD中点,证明:AF=AB.
10.如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.
(1)求证:DC=BE;
(2)若∠AEC=66°,求∠BCE的度数.
11.已知正方形ABCD中,点E和点G分别在边AD和BC上,连接AG交BE于点F,交BD于点K,若∠AKD=∠FBG.
(1)如图1,求证:∠BAG=∠EBD;
(2)如图2,连接DF并延长交AB于点H,若BH=FH=1,求DE长.
12.已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点,点F是BD的中点.
(1)求证:EF⊥BD;
(2)若∠BED=90°,求∠BCD的度数.
(3)若∠BED=α,直接写出∠BCD的度数.(用含α的代数式表示)
13.如图,AB∥CD,∠ACB=90°,E是AB的中点,CE=CD,DE和AC相交于点F.
求证:(1)DE⊥AC;
(2)∠ACD=∠ACE.
14.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=5,BC=12,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=70°,求∠FME的度数.
15.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,
(1)求证:DE∥BC;
(2)若AB=6,AC=10,点P为线段BC上一点,求BP长为多少时△DEP为等腰三角形?
参考答案
1.(1)证明:连接BE、DF,
∵四边形ABCD是平行四边形,
∴DO=BO,
∵OE=OF,
∴四边形DEBF是平行四边形,
∴DF=BE;
(2)解:当OE=DO时,四边形BEDF为矩形.
2.(1)证明:过点D作DN⊥AB于点N,
∵∠C=90°,DE⊥BC于点E,DF⊥AC于点F,
∴四边形FCED是矩形,
又∵∠A,∠B的平分线交于D点,
∴DF=DE=DN,
∴矩形FCED是正方形;
(2)解:∵AC=6,BC=8,∠C=90°,
∴AB=10,
∵四边形CEDF为正方形,
∴DF=DE=DN,
∴DF×AC+DE×BC+DN×AB=AC×BC,
则EC(AC+BC+AB)=AC×BC,
故EC==2.
3.证明:(1)∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,
同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF.
∴四边形ABEF是菱形.
(2)作FG⊥BC于G,
∵四边形ABEF是菱形,AE=6,BF=6,
∴AE⊥BF,OE=AE=3,OB=BF=3,
∴BE=,
∵S菱形ABEF=?AE?BF=BE?FG,
∴GF=3,
∴S平行四边形ABCD=BC?FG=27.
4.(1)证明:∵四边形ABCD是正方形,
∴AD=AB,AD∥BC,
∴∠DAB=∠ABE,∠ADO=∠BCO,
∵AB=BE,
∴AD=BE,
∴△ADO≌△BEO(ASA),
∴AO=BO;
(2)证明:延长BC至F,且使CF=BE,连接AF、DF,如图1所示:
则BF=CE,
∵四边形ABCD是矩形,
∴AB=DC,AD∥BC,∠BAD=∠ABC=∠DCB=90°,
在△ABF和△DCE中,,
∴△ABF≌△DCE(SAS),
∴∠DEC=∠AFB,
∵EB=CF,BN=CN,
∴N为EF的中点,
∴MN为△AEF的中位线,
∴MN∥AF,
∴∠HNB=∠AFB=∠HEB;
(3)解:过点B作BQ⊥BP交DE于Q,如图2所示:
则∠PBQ=90°,
∵∠ABE=180°﹣∠ABC=90°,
∴∠EBQ=∠ABP,
∵AD∥BC,
∴∠ADP=∠BEQ,
∵AP⊥DE,∠BAD=90°,
由角的互余关系得:∠BAP=∠ADP,
∴∠BEQ=∠BAP,
在△BEQ和△BAP中,,
∴△BEQ≌△BAP(ASA),
∴PA=QE,QB=PB,
∴△PBQ是等腰直角三角形,
∴PQ=PB,
∴==.
5.(1)解:∵D、E、M、N分别为AC、AB、OB、OC的中点,
∴DE∥BC,DE=BC,MN∥BC,MN=BC,
∴DE∥MN,DE=MN,
∴四边形EMND为平行四边形,
∴OM=OD,
∵OM=BM,
∴OB=2OM=2OD,
∴=2;
(2)当AB=AC时,四边形DEMN为矩形,
理由如下:∵D、E为AC、AB的中点,
∴AD=AC,AE=AB,
∴AD=AE,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(AAS),
∴BD=CE,
∵OD=OM=BM,
∴MD=BD,同理EN=EC,
∴MD=EN,
∴四边形DEMN为矩形;
(3)设DE=x,
∴BC=2x,
∵四边形DEMN是正方形,
∴OE=OD,OE⊥OD,
∴OE=OD=x,OB=x,
∴BE==x,
∴AB=x,
则==,
故答案为:.
6.解:(1)∵四边形AOBC为正方形,
∴OA=AC=CB=BO,∠OAC=∠ACB=∠CBO=∠BOA=90°,
∵E为AC的中点,
∴AE=EC=x,则AC=AO=2x,
在Rt△AOE中:,解得:x=1,
∴OA=AC=2,
∴C(2,2).
(2)①取BC中点M,延长OM交AC延长线于点N,
∵OA=OB,∠OAE=∠OBM,AE=BM,
∴△AOE≌△OBM(SAS),
∴∠AOE=∠BOM
又∵∠FOB=2∠AOE,
∴∠FOM=∠BOM=∠AOE,
又∵CN∥OB,
∴∠BOM=∠CNM,
∴∠FOM=∠FNO,
∴FO=FN,
∵BM=MC,∠MCN=∠MBO=90°,∠BOM=∠CNM,
∴△CMN≌△BMO(AAS),
∴CN=OB=2,
设CF=x,则AF=2﹣x,NF=2+x=FO,
在Rt△AOF中:AF2+AO2=OF2,
∴(2﹣x)2+22=(2+x)2,解得:x=0.5,
∴F(1.5,2).
②如图2,连接OH,AB,则AB=AC=2.
∵A与H关于AF对称,
∴∠AOF=∠HOF,OH=OA=OB,OF垂直平分AH,
作OP⊥BH于P,则∠BOP=∠HOP,
∵∠AOH+∠BOH=∠AOB=90°,
∴∠FOP=45°,
∵∠OQH=∠OPH=90°,
∴∠AHB=180°﹣∠FOP=135°,
∵F(1.5,2),
∴AF=1.5,
∴OF=2.5,
∴AH=2AQ===,
作BN⊥AH于N,则∠BHN=∠HBN=45°,
∴BN=HN=x,
∴BH=x,AN=AH+HN=+x,
在Rt△ANB中:AB2=AN2+BN2,
∴8=+x2,解得,(舍),
∴BH=.
7.解:(1)过A作AM⊥x轴于M,过C作CN⊥x轴于N,
∵A(﹣2,3),C(6,4),
∴AM=3ON=6,
∵矩形OABC中,∠AOC=90°,
∴∠MAO+∠AOM=∠AOM+∠CON=90°,
∴∠MAO=∠CON,
∴△AOM∽△OCN,
∴,
∴OC=2OA;
(2)过B作BH⊥x轴于H,过C作CE⊥BH于E,
则△AOM≌△BCE(AAS),
∴BE=AM=3,CE=OM=2,
∴BH=3+4=7,OH=6﹣2=4,
∴B(4,7);
(3)过A作AG⊥y轴于G,
∴OG=AM=3,
∵∠OAD=90°,
∴AO2=OG?OD,
∴AM2+OM2=13=3×OD,
∴OD=,
∴D(0,).
8.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,
∴∠ECF=∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF==10,
∴OC=EF=5;
(3)当△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
证明:∵O为AC中点,
∴OA=OC,
∵由(1)知OE=OF,
∴AO=EO=CO=FO,
∴?AECF为矩形,
又∵MN∥BC,∠ACB=90°,
∴∠AOE=∠ACB=90°,
∴AC⊥EF.
∴四边形AECF是正方形.
∴当△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
9.证明:(1)∵CE平分∠BCD,
∴∠ECD=∠FCB,
∵四边形ABCD是平行四边形,
∴∠FCD=∠BFC,
∴∠FCB=∠BFC,
∴BC=BF.
(2)∵E为AD中点,
∴DE=AE,
在△DEC与△AEF中,
∴△DEC≌△AEF(AAS),
∴AF=AB.
10.(1)证明:连接DE.
∵AD⊥BC,
∴∠ADB=90°,
∵AE=EB,
∴DE=EB=EA,
∵DG⊥EC,EG=GC,
∴DE=CD,
∴DC=BE.
(2)设∠BCE=x.
∵EB=DE=DC,
∴∠DCE=∠DEC=x,
∴∠EBD=∠BDE=∠DEC+∠DCE=2x,
∵∠AEC=∠EBD+∠ECD,
∴66°=3x,
∴x=22°,
∴∠BCE=22°.
11.(1)证明:如图1中,
∵四边形ABCD是正方形,
∴∠ABD=∠DBC=45°,
∵∠AKD=∠FBG,
∴∠ABD+∠BAG=∠DBC+∠EBD,
∴∠BAG=∠EBD.
(2)解:如图2中,作EP∥BD交AB于P,连接PF.AF交AF于O.
∵四边形ABCD是正方形,
∴∠ABD=∠ADB=45°,
∵EP∥BD,
∴∠APE=∠ABD,∠AEP=∠ADB,
∴∠APE=∠AEP=45°,
∴AP=AE,
∵AB=AD,
∴PB=DE,
∵∠OFE=∠ABF+∠BAF=∠ABF+∠EBD=45°,
∴∠APO=∠EFO,∵∠AOP=∠EOF,
∴△AOP∽△EOF,
∴=,
∴=,∵∠AOE=∠POF,
∴△AOE∽△POF,
∴∠PEO=∠AEO=45°,
∴∠PFE=∠BFP=90°,
∵BH=FH,
∴∠HBF=∠HFB,
∵∠HFB+∠BPF=90°,∠HFB+∠PFH=90°,
∴∠HPF=∠HFP,
∴FH=PH=BH=1,
∴PB=2,
∴DE=PB=2,
12.(1)证明:∵∠ABC=∠ADC=90°,点E是AC的中点,
∴DE=AC,BE=AC,
∴DE=BE,
∵点F是BD的中点,
∴EF⊥BD;
(2)解:∵∠ABC=∠ADC=90°,点E是AC的中点,
∴DE=AC=EC,BE=AC=EC,
∴∠EDC=∠DCE,∠EBC=∠ECB,
∵在四边形DEBC中,∠EDC+∠DCE+∠ECB+∠EBC+∠DEB=360°,
∵∠DEB=90°,
∵∠EDC+∠DCE+∠ECB+∠EBC=360°﹣∠DEB=360°﹣90°=270°,
∴2∠DCE+2∠ECB=270°,
∴∠DCE+∠ECB=135°,
即∠BCD=135°;
(3)若∠BED=α,则∠BCD=180°﹣,
理由是:∵∠ABC=∠ADC=90°,点E是AC的中点,
∴DE=AC=EC,BE=AC=EC,
∴∠EDC=∠DCE,∠EBC=∠ECB,
∵在四边形DEBC中,∠EDC+∠DCE+∠ECB+∠EBC+∠BED=360°,
∵∠BED=α,
∵∠EDC+∠DCE+∠ECB+∠EBC=360°﹣∠BED=360°﹣α,
∴2∠DCE+2∠ECB=360°﹣α,
∴∠DCE+∠ECB=180°﹣,
即∠BCD=180α.
13.证明:(1)直角三角形ACB中,
∵CE是斜边AB的中线,
∴CE=AE=BE=CD,
又∵AB∥CD,
∴BCDE为平行四边形,
∴BC∥DE,
∵AC⊥BC,
∴DE⊥AC.
(2)∵CD∥AB,
∴∠ACD=∠CAE.
由(1)知EC=EA,
∴∠A=∠ACE.
∴∠ACD=∠ACE.
14.解:(1)∵CF⊥AB于F,M为BC的中点,
∴ME=MC=BC=×12=6,
同理MF=MB=BC=×12=6,
∴△EFM的周长=6+6+5=17;
(2)∵MF=MB,
∴∠ABC=∠MFB=50°,
同理∠ACB=∠MEC=70°,
∴∠BMF=180°﹣50°﹣50°=80°,
∠EMC=180°﹣70°﹣70°=40°,
∴∠FME=180°﹣80°﹣40°=60°.
15.(1)证明:∵∠ABC=90°,点D是AC的中点,
∴BD=AD=AC,
∵DE是∠ADB的角平分线,
∴DE⊥AB,
又∵∠ABC=90°,
∴DE∥BC;
(2)解:由(1)知,DE∥BC,
又点D是AC的中点,
∴DE是△ABC的中位线,
∵AB=6,AC=10,
∴AE=3,AD=5,DE⊥AB,
∴DE===4,
∵DE⊥AB,AD=BD,
∴BE=AE=3,
①DE=EP时,BP==,
②DP=EP时,BP=DE=×4=2,
③DE=DP时,过点D作DF⊥BC于F,
则DF=BE=3,
由勾股定理得,FP==,
点P在F下边时,BP=4﹣,
点P在F上边时,BP=4+,
综上所述,BP的值为,2,4﹣,4+.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
