2020-2021学年苏科版七年级数学下册《第7章平面图形的认识二》高频易错题型优生辅导训练试卷(Word版附答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册《第7章平面图形的认识二》高频易错题型优生辅导训练试卷(Word版附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 230.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 07:39:29 | ||
图片预览



文档简介
2021年度苏科版七年级数学下册《第7章平面图形的认识二》
高频易错题型优生辅导训练(附答案)
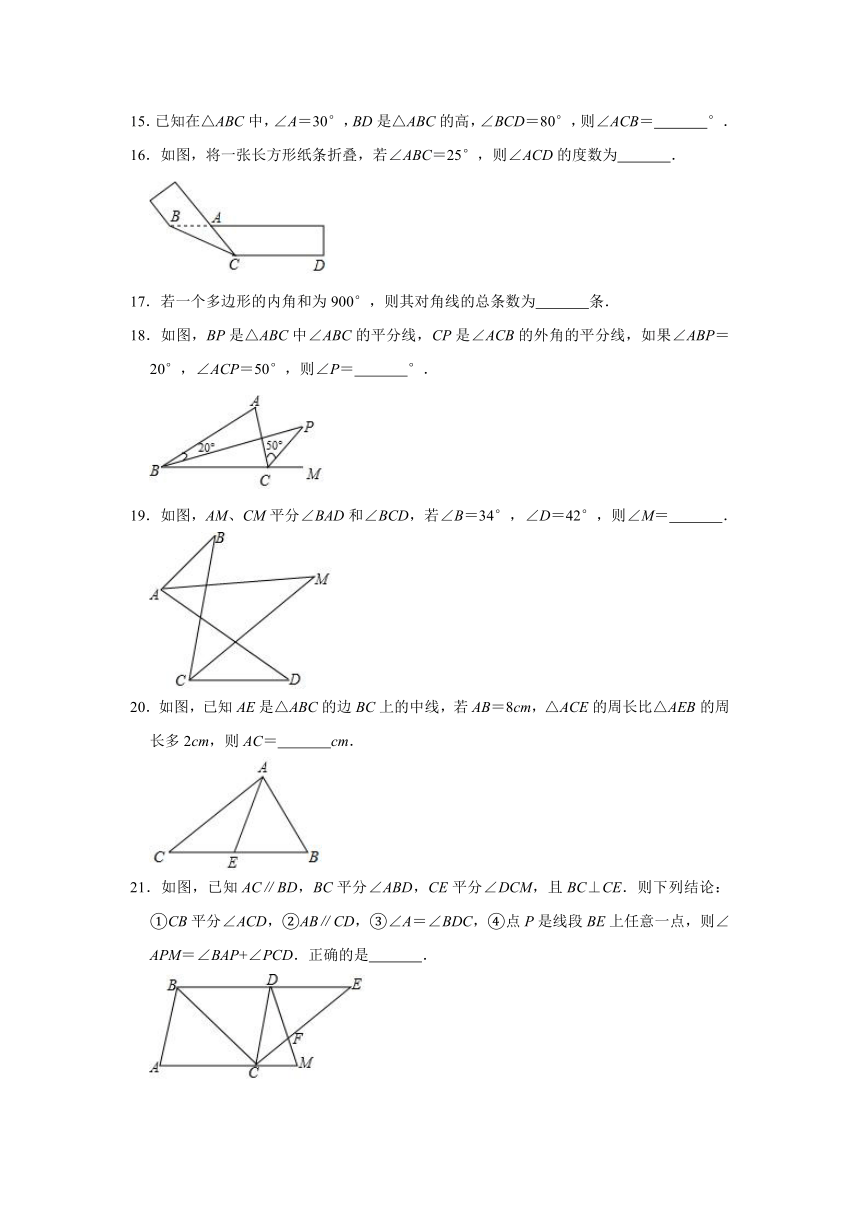
1.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;②∠BDC=∠BAC;③∠ADC=90°﹣∠ABD;④BD平分∠ADC.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
2.如图,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠2=44°,则∠1的大小为( )
A.14°
B.16°
C.24°
D.30°
3.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2
B.∠1+∠2
C.∠2﹣∠1
D.180°+∠2﹣2∠1
4.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )
A.50°、130°
B.都是10°
C.50°、130°或10°、10°
D.以上都不对
5.如图,已知AB∥CD,HI∥FG,EF⊥CD于F,∠1=40°,那么∠EHI=( )
A.60°
B.50°
C.45°
D.40°
6.下列说法:
①相等的角是对顶角;②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;④同角或等角的余角相等,
其中正确的说法有( )
A.4
个
B.3
个
C.2
个
D.1
个
7.如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列结论中:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BCD;④∠ABF=∠BCD,正确的有( )
A.1个
B.2个
C.3个
D.4个
8.在△ABC中,∠B、∠C的平分线交于点O,若∠BOC=132°,则∠A的度数为( )
A.42°
B.48°
C.84°
D.100°
9.如图,下面推理过程正确的是( )
A.因为∠B=∠BCD,所以AB∥CD
B.因为∠1=∠2,所以AB∥CD
C.因为∠BAD+∠B=180°,所以AD∥BC
D.因为∠1=∠B,所以AD∥BC
10.如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;②AC∥BE;③∠CBE+∠D=90°;④∠DEB=2∠ABC,
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
11.在△ABC中,2(∠A+∠B)=3∠C,则∠C的补角等于( )
A.36°
B.72°
C.108°
D.144°
12.如图,一条公路修到湖边时,需拐弯绕湖而过,若第一次拐角∠A=130°,第二次拐角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C为( )
A.170°
B.160°
C.150°
D.140°
13.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为
度.
14.如图,AB∥CD,CE交AB于F,∠C=55°,∠AEC=18°,则∠A=
°.
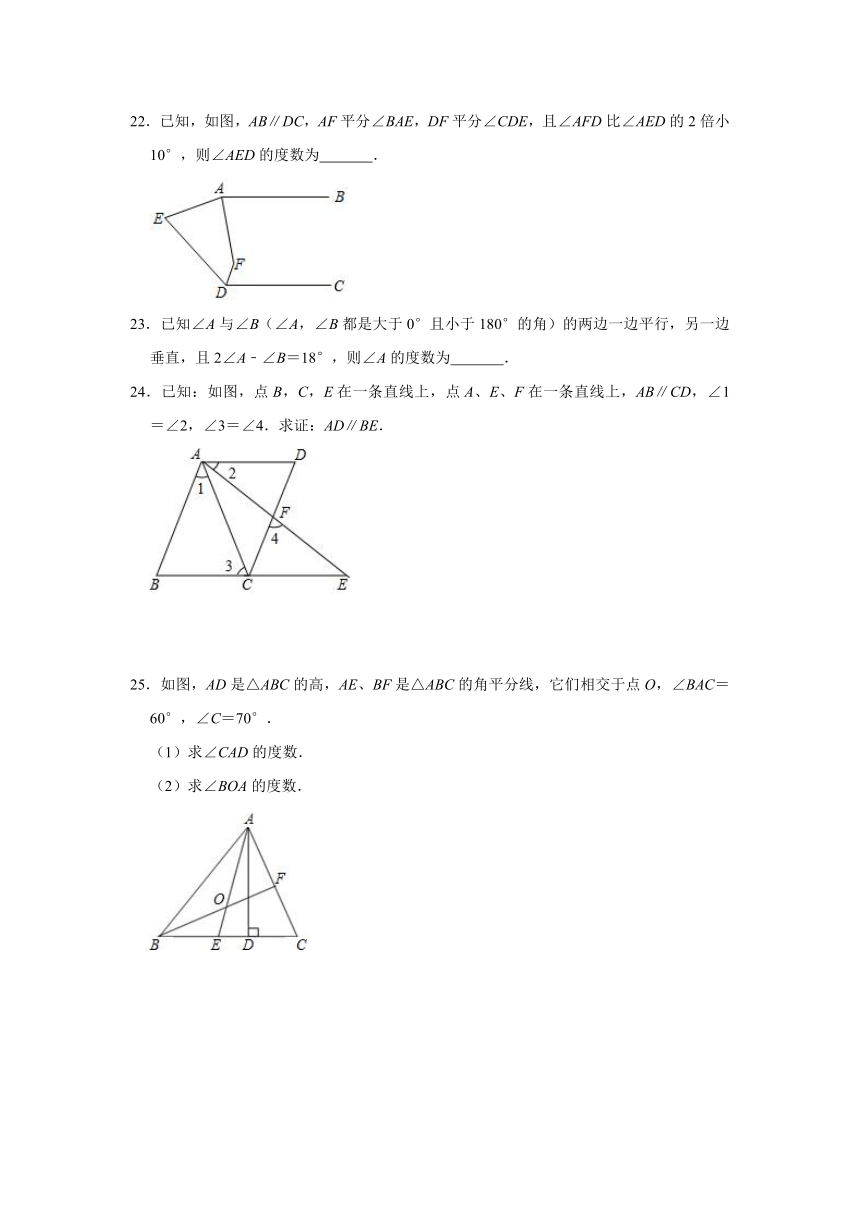
15.已知在△ABC中,∠A=30°,BD是△ABC的高,∠BCD=80°,则∠ACB=
°.
16.如图,将一张长方形纸条折叠,若∠ABC=25°,则∠ACD的度数为
.
17.若一个多边形的内角和为900°,则其对角线的总条数为
条.
18.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=
°.
19.如图,AM、CM平分∠BAD和∠BCD,若∠B=34°,∠D=42°,则∠M=
.
20.如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC=
cm.
21.如图,已知AC∥BD,BC平分∠ABD,CE平分∠DCM,且BC⊥CE.则下列结论:①CB平分∠ACD,②AB∥CD,③∠A=∠BDC,④点P是线段BE上任意一点,则∠APM=∠BAP+∠PCD.正确的是
.
22.已知,如图,AB∥DC,AF平分∠BAE,DF平分∠CDE,且∠AFD比∠AED的2倍小10°,则∠AED的度数为
.
23.已知∠A与∠B(∠A,∠B都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且2∠A﹣∠B=18°,则∠A的度数为
.
24.已知:如图,点B,C,E在一条直线上,点A、E、F在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.
25.如图,AD是△ABC的高,AE、BF是△ABC的角平分线,它们相交于点O,∠BAC=60°,∠C=70°.
(1)求∠CAD的度数.
(2)求∠BOA的度数.
26.如图,①∠D=∠B;②∠1=∠2;③∠3=∠4;④∠B+∠2+∠4=180°;⑤∠B+∠1+∠3=180°.
(1)指出上述各项中哪一项能作为题设来说明∠E=∠F;
(2)选出其中的一项加以说明.
27.众所周知,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等,如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射,若被b反射出的光线n与光线m平行,
(1)若∠1=50°,则∠2=
,∠3=
;
(2)若∠1=α,则∠2=
,∠3=
;
(3)结合(1)和(2),猜想:当两平面镜a、b的夹角∠3=
时,总有m∥n,并给出详细证明过程?
28.已知点F、G分别在直线AB、CD上,且知AB∥CD.
(1)如图1,请用等式表示∠GEF、∠BFE、∠CGE之间的数量关系并给出证明;
(2)如图2,∠BFE的平分线FQ所在的直线与∠CGE的平分线相交于点P,探究∠GPQ与∠GEF之间的数量关系,请直接写出你的结论:
.
参考答案
1.解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,即①正确;
∵BD、CD分别平分∠ABC、∠ACF
∴∠DCF=∠ACF,∠DBC=∠ABC,
∵∠DCF是△BCD的外角,
∴∠BDC=∠DCF﹣∠DBC=∠ACF﹣∠ABC=(∠ACF﹣∠ABC)=∠BAC,即②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=∠EAC,∠DCA=∠ACF,
∵∠EAC=∠ACB+∠ABC,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°﹣(∠DAC+∠ACD)
=180°﹣(∠EAC+∠ACF)=180°﹣(∠ABC+∠ACB+∠ABC+∠BAC)
=180°﹣(180°+∠ABC)=90°﹣∠ABC=90°﹣∠ABD,即③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°﹣∠ABC,
∴∠ADB不等于∠CDB,即④错误;
∴正确的有3个,
故选:C.
2.解:如图:
∵矩形的对边平行,
∴∠2=∠3=44°,
根据三角形外角性质,可得∠3=∠1+30°,
∴∠1=44°﹣30°=14°,
故选:A.
3.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
4.解:∵两个角的两边分别平行,
∴这两个角相等或互补.
设其中一角为x°,
若这两个角相等,则x=3x﹣20,
解得:x=10,
∴这两个角的度数是10°和10°;
若这两个角互补,
则180﹣x=3x﹣20,解得:x=50,
∴这两个角的度数是50°和130°.
∴这两个角的度数是50°、130°或10°、10°.故选:C.
5.解:∵AB∥CD,∠1=40°,
∴∠GFD=∠1=40°,
∵EF⊥CD,
∴∠EFD=90°,
∴∠EFG=∠EFD﹣∠GFD=90°﹣40°=50°,
又∵HI∥FG,
∴∠EHI=∠EFG=50°,
故选:B.
6.解:①相等的角不一定是对顶角,原说法错误;
②平面内,过一点有且只有一条直线与已知直线垂直,原说法正确;
③平行于同一条直线的两条直线互相平行,原说法正确;
④同角或等角的余角相等,原说法正确.
正确的说法有3个,
故选:B.
7.解:∵BC∥DE,
∴∠ACB=∠E,故①正确;
∵BC∥DE,
∴∠ABC=∠ADE,
∵BF平分∠ABC,DC平分∠ADE,
∴∠ABF=∠CBF=∠ABC,∠ADC=∠EDC=∠ADE,
∴∠ABF=∠CBF=∠ADC=∠EDC,
∴BF∥DC,
∴∠BFD=∠FDC,
根据已知不能得出∠ADF=∠CDF,
即不能得出DF平分∠ADC,故②错误;
∵∠FDC≠∠BCD,
∴∠BFD≠∠BCD,③错误;
∵∠ABF=∠ADC,∠ADC=∠EDC,
∴∠ABF=∠EDC,
∵DE∥BC,
∴∠BCD=∠EDC,
∴∠ABF=∠BCD,故④正确;
即正确的有2个,
故选:B.
8.解:如图:∵∠BOC=132°,∠BOC+∠OBC+∠OCB=180°,
∴∠OBC+∠OCB=180°﹣132°=48°,
∵∠ABC与∠ACB的平分线相交于点O,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=96°,
∴∠A=180°﹣96°=84°,
故选:C.
9.解:A、因为∠B+∠BCD=180°,所以AB∥CD,原说法错误,故此选项不符合题意;
B、因为∠1=∠2,所以AD∥BC,原说法错误,故此选项不符合题意;
C、因为∠BAD+∠B=180°,所以AD∥BC,原说法正确,故此选项符合题意;
D、因为∠1=∠2,所以AD∥BC,原说法错误,故此选项不符合题意;
故选:C.
10.解:∵AF∥CD,
∴∠ABC=∠ECB,∠EDB=∠DBF,∠DEB=∠EBA,
∵CB平分∠ACD,BD平分∠EBF,
∴∠ECB=∠BCA,∠EBD=∠DBF,
∴∠EDB=∠DBE,
∵BC⊥BD,
∴∠EDB+∠ECB=90°,∠DBE+∠EBC=90°,
∴∠ECB=∠EBC,
∴∠ECB=∠EBC=∠ABC=∠BCA,
∴BC平分∠ABE,①正确;
∵∠EBC=∠BCA,
∴AC∥BE,②正确;
∴∠CBE+∠EDB=90°,③正确;
∵∠DEB=∠EBA=2∠ABC,故④正确;
故选:D.
11.解:∵2(∠A+∠B)=3∠C,∠A+∠B=180°﹣∠C,
∴2(180°﹣∠C)=3∠C,
∴∠C=72°,
∴∠C的补角等于108°,
故选:C.
12.解:如图,过点B作BD∥AE,
由已知可得:AE∥CF,
∴AE∥BD∥CF,
∴∠ABD=∠A=130°,∠DBC+∠C=180°,
∴∠DBC=∠ABC﹣∠ABD=150°﹣130°=20°,
∴∠C=180°﹣∠DBC=180°﹣20°=160°.
故选:B.
13.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
14.解:∵AB∥CD,∠C=55°,
∴∠EFB=∠C=55°,
∴∠AFE=180°﹣∠EFB=125°,
∵∠AEC=18°,
∴∠A=180°﹣∠AFE﹣∠AEC=37°,
故答案为:37.
15.解:(1)如图,当△ABC为锐角三角形时,
∠ACB=∠BCD=80°,
(2)如图,当△ABC为钝角三角形时,
∠ACB=180°﹣∠BCD=100°.
故答案为:80°或100.
16.解:延长DC到点E,如图:
∵AB∥CD,
∴∠BCE=∠ABC=25°,
由折叠可得:∠ACB=∠BCE=25°,
∵∠BCE+∠ACB+∠ACD=180°,
∴∠ACD=180°﹣∠BCE﹣∠ACB=180°﹣25°﹣25°=130°,
故答案为:130°.
17.解:设这个多边形的边数为n,
则(n﹣2)×180°=900°,
解得,n=7,
∴七边形的对角线的总条数为:×7×4=14,
故答案为:14.
18.解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,
∵∠PCM是△BCP的外角,
∴∠P=∠PCM﹣∠CBP=50°﹣20°=30°,
故答案为:30°.
19.解:∵∠B+∠BAM=∠M+∠BCM,
∴∠BAM﹣∠BCM=∠M﹣∠B,
同理,∠MAD﹣∠MCD=∠D﹣∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M﹣∠B=∠D﹣∠M,
∴∠M=(∠B+∠D)=(34°+42°)=38°.
故答案为38°.
20.解:∵AE是△ABC的边BC上的中线,
∴CE=BE,
又∵AE=AE,△ACE的周长比△AEB的周长多2cm,
∴AC﹣AB=2cm,
即AC﹣8=2cm,
∴AC=10cm,
故答案为:10;
21.解:如图,
∵AC∥BD,
∵∠2=∠3
∵BC平分∠ABD,
∴∠1=∠2,
∴∠1=∠3,
∵CE平分∠DCM,
∴∠4=∠5,
∵BC⊥CE.
∴∠4+∠6=90°,
∴∠5+∠6=90°,
∵∠3+∠5=90°,
∴∠3=∠6,
∴CB平分∠ACD,故①正确;
∴∠1=∠6,
AB∥CD,故②正确;
∴四边形ABCD是平行四边形,
∴∠A=∠BDC,故③正确;
如图,点P是线段BE上任意一点,
∵AB与PC不平行,CD与PM不平行,
∴∠BAP≠∠APC,∠PCD≠∠CPM,
∴∠APM≠∠BAP+∠PCD.故④不正确.
所以正确的是①②③.
故答案为:①②③.
22.解:如图所示,过F作FG∥AB,
∵AB∥DC,
∴AB∥GF∥CD,
∴∠1=∠DFG,∠2=∠AFG,
∴∠AFD=∠1+∠2,
∵AF平分∠BAE,DF平分∠CDE,
∴∠1=∠3,∠2=∠4,
设∠E=α,则∠AFD=2α﹣10°,
∴∠AFD=∠3+∠4=2α﹣10°,
∵四边形AEDF中,∠E+∠3+∠4+∠AFD=360°,
∴α+2(2α﹣10°)=360°,
解得α=76°,
故答案为:76°.
23.解:①如图所示,∵AD∥BE,∠ACB=90°,
∴∠A+∠B=90°,
又∵2∠A﹣∠B=18°,
∴3∠A=108°,
∴∠A=36°;
②如图所示,∵AD∥BE,∠ACB=90°,
∴∠A+∠B=360°﹣90°=270°,
又∵2∠A﹣∠B=18°,
∴3∠A=288°,
∴∠A=96°;
综上所述,∠A的度数为36°或96°,
故答案为:36°或96°.
24.证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠2=∠ACD,
∴∠2+∠CAE=∠ACD+∠CAE,
∴∠DAC=∠4,
∵∠3=∠4,
∴∠DAC=∠3,
∴AD∥BE.
25.解:(1)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣90°﹣70°=20°;
(2)∵∠BAC=60°,∠C=70°,
∴∠BAO=30°,∠ABC=50°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣30°﹣25°=125°.
26.解:(1)②∠1=∠2,或⑤∠B+∠1+∠3=180°.
(2)选∠1=∠2加以说明.
∵∠1=∠2,
∴AD∥CB(内错角相等,两直线平行),
∴∠E=∠F(两直线平行,内错角相等).
27.解:(1)∵∠1=∠4=50°,
∴∠5=180°﹣2×50°=80°,
∵m∥n,
∴∠2+∠5=180°,
∴∠2=100°,
∴∠6=(180°﹣∠2)=40°,
∴∠3=180°﹣∠4﹣∠6=90°;
(2)∵∠1=∠4=α,
∴∠5=180°﹣2α,
∵m∥n,
∴∠2+∠5=180°,
∴∠2=2α,
∴∠6=(180°﹣∠2)=90°﹣α,
∴∠3=180°﹣∠4﹣∠6=90°;
(3)当∠3=90°时,m∥n.理由如下:
∵∠3=90°,
∴∠4+∠6=90°,
∴2∠4+2∠6=180°,
∴∠2+∠5=180°,
∴m∥n.
故答案为:100°,90°;2α,90°;90°.
28.解:(1)∠GEF=∠BFE+180°﹣∠CGE,证明如下:
如图1,过E作EH∥AB,
∵AB∥CD
∴AB∥CD∥EH,
∴∠HEF=∠BFE,∠HEG+∠CGE=180°,
∴∠HEF+∠HEG=∠BFE+180°﹣∠CGE,
∴∠GEF=∠BFE+180°﹣∠CGE;
(2)∠GPQ+∠GEF=90°,理由是:
∵FQ平分∠BFE,GP平分∠CGE,
∴∠BFQ=∠BFE,∠CGP=∠CGE,
△PMF中,∠GPQ=∠GMF﹣∠PFM=∠CGP﹣∠BFQ,
∴∠GPQ+∠GEF=∠CGE﹣∠BFE+∠GEF=×180°=90°.
故答案为:∠GPQ+∠GEF=90°
高频易错题型优生辅导训练(附答案)
1.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;②∠BDC=∠BAC;③∠ADC=90°﹣∠ABD;④BD平分∠ADC.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
2.如图,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠2=44°,则∠1的大小为( )
A.14°
B.16°
C.24°
D.30°
3.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2
B.∠1+∠2
C.∠2﹣∠1
D.180°+∠2﹣2∠1
4.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )
A.50°、130°
B.都是10°
C.50°、130°或10°、10°
D.以上都不对
5.如图,已知AB∥CD,HI∥FG,EF⊥CD于F,∠1=40°,那么∠EHI=( )
A.60°
B.50°
C.45°
D.40°
6.下列说法:
①相等的角是对顶角;②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;④同角或等角的余角相等,
其中正确的说法有( )
A.4
个
B.3
个
C.2
个
D.1
个
7.如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列结论中:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BCD;④∠ABF=∠BCD,正确的有( )
A.1个
B.2个
C.3个
D.4个
8.在△ABC中,∠B、∠C的平分线交于点O,若∠BOC=132°,则∠A的度数为( )
A.42°
B.48°
C.84°
D.100°
9.如图,下面推理过程正确的是( )
A.因为∠B=∠BCD,所以AB∥CD
B.因为∠1=∠2,所以AB∥CD
C.因为∠BAD+∠B=180°,所以AD∥BC
D.因为∠1=∠B,所以AD∥BC
10.如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;②AC∥BE;③∠CBE+∠D=90°;④∠DEB=2∠ABC,
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
11.在△ABC中,2(∠A+∠B)=3∠C,则∠C的补角等于( )
A.36°
B.72°
C.108°
D.144°
12.如图,一条公路修到湖边时,需拐弯绕湖而过,若第一次拐角∠A=130°,第二次拐角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C为( )
A.170°
B.160°
C.150°
D.140°
13.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为
度.
14.如图,AB∥CD,CE交AB于F,∠C=55°,∠AEC=18°,则∠A=
°.
15.已知在△ABC中,∠A=30°,BD是△ABC的高,∠BCD=80°,则∠ACB=
°.
16.如图,将一张长方形纸条折叠,若∠ABC=25°,则∠ACD的度数为
.
17.若一个多边形的内角和为900°,则其对角线的总条数为
条.
18.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=
°.
19.如图,AM、CM平分∠BAD和∠BCD,若∠B=34°,∠D=42°,则∠M=
.
20.如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC=
cm.
21.如图,已知AC∥BD,BC平分∠ABD,CE平分∠DCM,且BC⊥CE.则下列结论:①CB平分∠ACD,②AB∥CD,③∠A=∠BDC,④点P是线段BE上任意一点,则∠APM=∠BAP+∠PCD.正确的是
.
22.已知,如图,AB∥DC,AF平分∠BAE,DF平分∠CDE,且∠AFD比∠AED的2倍小10°,则∠AED的度数为
.
23.已知∠A与∠B(∠A,∠B都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且2∠A﹣∠B=18°,则∠A的度数为
.
24.已知:如图,点B,C,E在一条直线上,点A、E、F在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.
25.如图,AD是△ABC的高,AE、BF是△ABC的角平分线,它们相交于点O,∠BAC=60°,∠C=70°.
(1)求∠CAD的度数.
(2)求∠BOA的度数.
26.如图,①∠D=∠B;②∠1=∠2;③∠3=∠4;④∠B+∠2+∠4=180°;⑤∠B+∠1+∠3=180°.
(1)指出上述各项中哪一项能作为题设来说明∠E=∠F;
(2)选出其中的一项加以说明.
27.众所周知,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等,如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射,若被b反射出的光线n与光线m平行,
(1)若∠1=50°,则∠2=
,∠3=
;
(2)若∠1=α,则∠2=
,∠3=
;
(3)结合(1)和(2),猜想:当两平面镜a、b的夹角∠3=
时,总有m∥n,并给出详细证明过程?
28.已知点F、G分别在直线AB、CD上,且知AB∥CD.
(1)如图1,请用等式表示∠GEF、∠BFE、∠CGE之间的数量关系并给出证明;
(2)如图2,∠BFE的平分线FQ所在的直线与∠CGE的平分线相交于点P,探究∠GPQ与∠GEF之间的数量关系,请直接写出你的结论:
.
参考答案
1.解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,即①正确;
∵BD、CD分别平分∠ABC、∠ACF
∴∠DCF=∠ACF,∠DBC=∠ABC,
∵∠DCF是△BCD的外角,
∴∠BDC=∠DCF﹣∠DBC=∠ACF﹣∠ABC=(∠ACF﹣∠ABC)=∠BAC,即②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=∠EAC,∠DCA=∠ACF,
∵∠EAC=∠ACB+∠ABC,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°﹣(∠DAC+∠ACD)
=180°﹣(∠EAC+∠ACF)=180°﹣(∠ABC+∠ACB+∠ABC+∠BAC)
=180°﹣(180°+∠ABC)=90°﹣∠ABC=90°﹣∠ABD,即③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°﹣∠ABC,
∴∠ADB不等于∠CDB,即④错误;
∴正确的有3个,
故选:C.
2.解:如图:
∵矩形的对边平行,
∴∠2=∠3=44°,
根据三角形外角性质,可得∠3=∠1+30°,
∴∠1=44°﹣30°=14°,
故选:A.
3.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
4.解:∵两个角的两边分别平行,
∴这两个角相等或互补.
设其中一角为x°,
若这两个角相等,则x=3x﹣20,
解得:x=10,
∴这两个角的度数是10°和10°;
若这两个角互补,
则180﹣x=3x﹣20,解得:x=50,
∴这两个角的度数是50°和130°.
∴这两个角的度数是50°、130°或10°、10°.故选:C.
5.解:∵AB∥CD,∠1=40°,
∴∠GFD=∠1=40°,
∵EF⊥CD,
∴∠EFD=90°,
∴∠EFG=∠EFD﹣∠GFD=90°﹣40°=50°,
又∵HI∥FG,
∴∠EHI=∠EFG=50°,
故选:B.
6.解:①相等的角不一定是对顶角,原说法错误;
②平面内,过一点有且只有一条直线与已知直线垂直,原说法正确;
③平行于同一条直线的两条直线互相平行,原说法正确;
④同角或等角的余角相等,原说法正确.
正确的说法有3个,
故选:B.
7.解:∵BC∥DE,
∴∠ACB=∠E,故①正确;
∵BC∥DE,
∴∠ABC=∠ADE,
∵BF平分∠ABC,DC平分∠ADE,
∴∠ABF=∠CBF=∠ABC,∠ADC=∠EDC=∠ADE,
∴∠ABF=∠CBF=∠ADC=∠EDC,
∴BF∥DC,
∴∠BFD=∠FDC,
根据已知不能得出∠ADF=∠CDF,
即不能得出DF平分∠ADC,故②错误;
∵∠FDC≠∠BCD,
∴∠BFD≠∠BCD,③错误;
∵∠ABF=∠ADC,∠ADC=∠EDC,
∴∠ABF=∠EDC,
∵DE∥BC,
∴∠BCD=∠EDC,
∴∠ABF=∠BCD,故④正确;
即正确的有2个,
故选:B.
8.解:如图:∵∠BOC=132°,∠BOC+∠OBC+∠OCB=180°,
∴∠OBC+∠OCB=180°﹣132°=48°,
∵∠ABC与∠ACB的平分线相交于点O,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=96°,
∴∠A=180°﹣96°=84°,
故选:C.
9.解:A、因为∠B+∠BCD=180°,所以AB∥CD,原说法错误,故此选项不符合题意;
B、因为∠1=∠2,所以AD∥BC,原说法错误,故此选项不符合题意;
C、因为∠BAD+∠B=180°,所以AD∥BC,原说法正确,故此选项符合题意;
D、因为∠1=∠2,所以AD∥BC,原说法错误,故此选项不符合题意;
故选:C.
10.解:∵AF∥CD,
∴∠ABC=∠ECB,∠EDB=∠DBF,∠DEB=∠EBA,
∵CB平分∠ACD,BD平分∠EBF,
∴∠ECB=∠BCA,∠EBD=∠DBF,
∴∠EDB=∠DBE,
∵BC⊥BD,
∴∠EDB+∠ECB=90°,∠DBE+∠EBC=90°,
∴∠ECB=∠EBC,
∴∠ECB=∠EBC=∠ABC=∠BCA,
∴BC平分∠ABE,①正确;
∵∠EBC=∠BCA,
∴AC∥BE,②正确;
∴∠CBE+∠EDB=90°,③正确;
∵∠DEB=∠EBA=2∠ABC,故④正确;
故选:D.
11.解:∵2(∠A+∠B)=3∠C,∠A+∠B=180°﹣∠C,
∴2(180°﹣∠C)=3∠C,
∴∠C=72°,
∴∠C的补角等于108°,
故选:C.
12.解:如图,过点B作BD∥AE,
由已知可得:AE∥CF,
∴AE∥BD∥CF,
∴∠ABD=∠A=130°,∠DBC+∠C=180°,
∴∠DBC=∠ABC﹣∠ABD=150°﹣130°=20°,
∴∠C=180°﹣∠DBC=180°﹣20°=160°.
故选:B.
13.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
14.解:∵AB∥CD,∠C=55°,
∴∠EFB=∠C=55°,
∴∠AFE=180°﹣∠EFB=125°,
∵∠AEC=18°,
∴∠A=180°﹣∠AFE﹣∠AEC=37°,
故答案为:37.
15.解:(1)如图,当△ABC为锐角三角形时,
∠ACB=∠BCD=80°,
(2)如图,当△ABC为钝角三角形时,
∠ACB=180°﹣∠BCD=100°.
故答案为:80°或100.
16.解:延长DC到点E,如图:
∵AB∥CD,
∴∠BCE=∠ABC=25°,
由折叠可得:∠ACB=∠BCE=25°,
∵∠BCE+∠ACB+∠ACD=180°,
∴∠ACD=180°﹣∠BCE﹣∠ACB=180°﹣25°﹣25°=130°,
故答案为:130°.
17.解:设这个多边形的边数为n,
则(n﹣2)×180°=900°,
解得,n=7,
∴七边形的对角线的总条数为:×7×4=14,
故答案为:14.
18.解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,
∵∠PCM是△BCP的外角,
∴∠P=∠PCM﹣∠CBP=50°﹣20°=30°,
故答案为:30°.
19.解:∵∠B+∠BAM=∠M+∠BCM,
∴∠BAM﹣∠BCM=∠M﹣∠B,
同理,∠MAD﹣∠MCD=∠D﹣∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M﹣∠B=∠D﹣∠M,
∴∠M=(∠B+∠D)=(34°+42°)=38°.
故答案为38°.
20.解:∵AE是△ABC的边BC上的中线,
∴CE=BE,
又∵AE=AE,△ACE的周长比△AEB的周长多2cm,
∴AC﹣AB=2cm,
即AC﹣8=2cm,
∴AC=10cm,
故答案为:10;
21.解:如图,
∵AC∥BD,
∵∠2=∠3
∵BC平分∠ABD,
∴∠1=∠2,
∴∠1=∠3,
∵CE平分∠DCM,
∴∠4=∠5,
∵BC⊥CE.
∴∠4+∠6=90°,
∴∠5+∠6=90°,
∵∠3+∠5=90°,
∴∠3=∠6,
∴CB平分∠ACD,故①正确;
∴∠1=∠6,
AB∥CD,故②正确;
∴四边形ABCD是平行四边形,
∴∠A=∠BDC,故③正确;
如图,点P是线段BE上任意一点,
∵AB与PC不平行,CD与PM不平行,
∴∠BAP≠∠APC,∠PCD≠∠CPM,
∴∠APM≠∠BAP+∠PCD.故④不正确.
所以正确的是①②③.
故答案为:①②③.
22.解:如图所示,过F作FG∥AB,
∵AB∥DC,
∴AB∥GF∥CD,
∴∠1=∠DFG,∠2=∠AFG,
∴∠AFD=∠1+∠2,
∵AF平分∠BAE,DF平分∠CDE,
∴∠1=∠3,∠2=∠4,
设∠E=α,则∠AFD=2α﹣10°,
∴∠AFD=∠3+∠4=2α﹣10°,
∵四边形AEDF中,∠E+∠3+∠4+∠AFD=360°,
∴α+2(2α﹣10°)=360°,
解得α=76°,
故答案为:76°.
23.解:①如图所示,∵AD∥BE,∠ACB=90°,
∴∠A+∠B=90°,
又∵2∠A﹣∠B=18°,
∴3∠A=108°,
∴∠A=36°;
②如图所示,∵AD∥BE,∠ACB=90°,
∴∠A+∠B=360°﹣90°=270°,
又∵2∠A﹣∠B=18°,
∴3∠A=288°,
∴∠A=96°;
综上所述,∠A的度数为36°或96°,
故答案为:36°或96°.
24.证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠2=∠ACD,
∴∠2+∠CAE=∠ACD+∠CAE,
∴∠DAC=∠4,
∵∠3=∠4,
∴∠DAC=∠3,
∴AD∥BE.
25.解:(1)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣90°﹣70°=20°;
(2)∵∠BAC=60°,∠C=70°,
∴∠BAO=30°,∠ABC=50°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣30°﹣25°=125°.
26.解:(1)②∠1=∠2,或⑤∠B+∠1+∠3=180°.
(2)选∠1=∠2加以说明.
∵∠1=∠2,
∴AD∥CB(内错角相等,两直线平行),
∴∠E=∠F(两直线平行,内错角相等).
27.解:(1)∵∠1=∠4=50°,
∴∠5=180°﹣2×50°=80°,
∵m∥n,
∴∠2+∠5=180°,
∴∠2=100°,
∴∠6=(180°﹣∠2)=40°,
∴∠3=180°﹣∠4﹣∠6=90°;
(2)∵∠1=∠4=α,
∴∠5=180°﹣2α,
∵m∥n,
∴∠2+∠5=180°,
∴∠2=2α,
∴∠6=(180°﹣∠2)=90°﹣α,
∴∠3=180°﹣∠4﹣∠6=90°;
(3)当∠3=90°时,m∥n.理由如下:
∵∠3=90°,
∴∠4+∠6=90°,
∴2∠4+2∠6=180°,
∴∠2+∠5=180°,
∴m∥n.
故答案为:100°,90°;2α,90°;90°.
28.解:(1)∠GEF=∠BFE+180°﹣∠CGE,证明如下:
如图1,过E作EH∥AB,
∵AB∥CD
∴AB∥CD∥EH,
∴∠HEF=∠BFE,∠HEG+∠CGE=180°,
∴∠HEF+∠HEG=∠BFE+180°﹣∠CGE,
∴∠GEF=∠BFE+180°﹣∠CGE;
(2)∠GPQ+∠GEF=90°,理由是:
∵FQ平分∠BFE,GP平分∠CGE,
∴∠BFQ=∠BFE,∠CGP=∠CGE,
△PMF中,∠GPQ=∠GMF﹣∠PFM=∠CGP﹣∠BFQ,
∴∠GPQ+∠GEF=∠CGE﹣∠BFE+∠GEF=×180°=90°.
故答案为:∠GPQ+∠GEF=90°
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
