2020-2021学年八年级数学人教版下册第16章二次根式课后巩固提升训练(word解析版)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第16章二次根式课后巩固提升训练(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 274.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 14:15:58 | ||
图片预览



文档简介
2021年度人教版版八年级数学下册《第16章二次根式》课后巩固提升训练(附答案)
1.下列计算正确的是( )
A.=
B.=×
C.4=3
D.=
2.若2<a<3,则等于( )
A.5﹣2a
B.1﹣2a
C.2a﹣5
D.2a﹣1
3.已知:a=,b=,则a与b的关系是( )
A.a﹣b=0
B.a+b=0
C.ab=1
D.a2=b2
4.计算(﹣3)2020(+3)2021的值为( )
A.1
B.+3
C.﹣3
D.3
5.若代数式有意义,则x的取值范围是( )
A.x>且x≠3
B.x≥
C.x≥且x≠3
D.x≤且x≠﹣3
6.下列根式中,与不是同类二次根式的是( )
A.
B.
C.
D.
7.把根号外的因式移入根号内得( )
A.
B.
C.
D.
8.下列各式中,一定是二次根式的个数为( )
,,,,,(a≥0),(a<)
A.3个
B.4个
C.5个
D.6个
9.在、、、、中,最简二次根式有( )
A.1个
B.2个
C.3个
D.4个
10.若式子有意义,则实数x的取值范围是
.
11.﹣=
.
12.=2,=3,=4,…观察下列各式:请你找出其中规律,并将第n(n≥1)个等式写出来
.
13.计算的结果为
.
14.已知0<a<1,化简=
.
15.若的值是整数,则自然数x的值为
.
16.若代数式有意义,则x的取值范围是
17.已知a,b在数轴上的位置如图,化简:=
.
18.不等式x﹣>0的解集是
.
19.若一直角三角形两直角边的长分别为,,则这个直角三角形斜边上的中线为
.
20.计算:
(1);
(2).
21.观察下列一组式的变形过程,然后回答问题:
例1:,
例2:,,
(1)=
;=
(2)请你用含n(n为正整数)的关系式表示上述各式子的变形规律.
(3)利用上面的结论,求下列式子的值..
22.计算:.
23.已知a=,b=.
(1)求a+b的值;
(2)设m是a小数部分,n是b整数部分,求代数式4m2+4mn+n2的值.
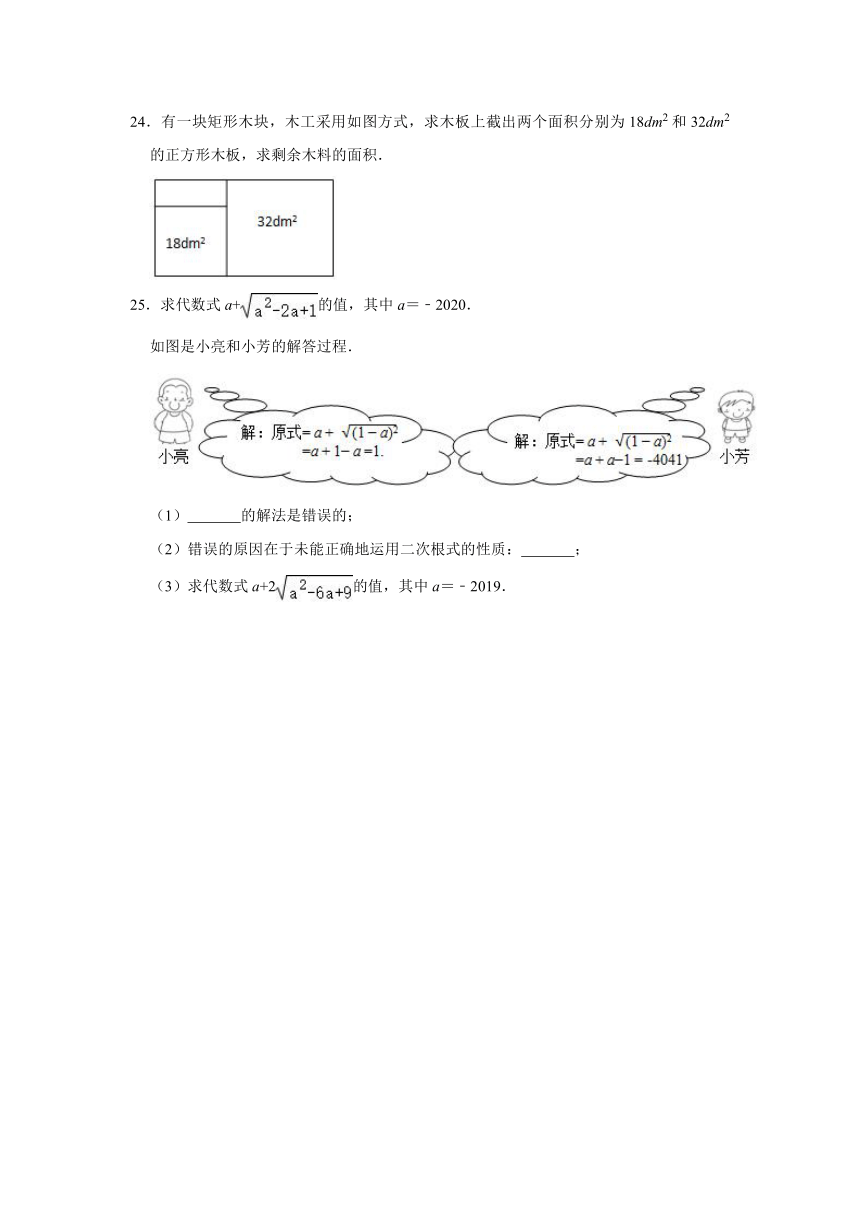
24.有一块矩形木块,木工采用如图方式,求木板上截出两个面积分别为18dm2和32dm2的正方形木板,求剩余木料的面积.
25.求代数式a+的值,其中a=﹣2020.
如图是小亮和小芳的解答过程.
(1)
的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质:
;
(3)求代数式a+2的值,其中a=﹣2019.
参考答案
1.解:A、+,无法计算,故此选项错误;
B、=×,故此选项错误;
C、4﹣=3,故此选项错误;
D、?=,故此选项正确.故选:D.
2.解:∵2<a<3,
∴=a﹣2﹣(3﹣a)=a﹣2﹣3+a=2a﹣5.故选:C.
3.解:分母有理化,可得a=2+,b=2﹣,
∴a﹣b=(2+)﹣(2﹣)=2,故A选项错误;
a+b=(2+)+(2﹣)=4,故B选项错误;
ab=(2+)×(2﹣)=4﹣3=1,故C选项正确;
∵a2=(2+)2=4+4+3=7+4,b2=(2﹣)2=4﹣4+3=7﹣4,
∴a2≠b2,故D选项错误;故选:C.
4.解:原式=(﹣3)2018(+3)2018×(+3)
=[(﹣3)(+3)]2018×(+3)
=(10﹣9)2018×(+3)=1×(+3)=+3,故选:B.
5.解:∵代数式有意义,
∴3x﹣2≥0,|x|﹣3≠0,
解得:x≥且x≠3.故选:C.
6.解:A、,与是同类二次根式;
B、,与是同类二次根式;
C、,与是同类二次根式;
D、与不是同类二次根式,故选:D.
7.解:∵成立,
∴﹣>0,即m<0,
∴原式=﹣=﹣.
故选:D.
8.解:一定是二次根式;
当m<0时,不是二次根式;
对于任意的数x,x2+1>0,则一定是二次根式;
是三次方根,不是二次根式;
﹣m2﹣1<0,则不是二次根式;
是二次根式;
当a<时,2a+1可能小于0,不是二次根式.
故选:A.
9.解:在、、、、中,最简二次根式为、.
故选:B.
10.解:∵式子有意义,
∴x+1≥0,x≠0,
解得:x≥﹣1且x≠0.
故答案为:x≥﹣1且x≠0.
11.解:原式=3﹣2=,
故答案为:.
12.解:由=2,=3,=4,…得
=(n+1),
故答案为:=(n+1).
13.解:原式=3﹣2=.
故答案为:.
14.解:∵0<a<1,
∴<,
∴原式=﹣
=﹣
=﹣()=2.
15.解:由题意得:x≤17,
当x=0时,原式=,不合题意;
当x=1时,原式==4;
当x=2时,原式=,不合题意;
当x=3时,原式=,不合题意;
当x=4时,原式=,不合题意;
当x=5时,原式==2,不合题意;
当x=6时,原式=,不合题意;
当x=7时,原式=,不合题意;
当x=8时,原式==3;
当x=9时,原式==2,不合题意;
当x=10时,原式=,不合题意;
当x=11时,原式=,不合题意;
当x=12时,原式=,不合题意;
当x=13时,原式==2;
当x=14时,原式=,不合题意;
当x=15时,原式=,不合题意;
当x=16时,原式=1;
当x=17时,原式=0.
综上所述,x=1、8、13、16或17.
16.解:若代数式有意义,
必有
解得﹣3≤x<且x≠﹣2.
17.解:由a,b在数轴上的位置可知:﹣2<a<﹣1,2<b<3,
∴=﹣(a+1)+2﹣b=1﹣a﹣b.
18.解:x﹣>0
,
故答案为:x.
19.解:∵一直角三角形两直角边的长分别为,,
∴斜边长为:=2,
∴这个直角三角形斜边上的中线为,
故答案为:.
20.解:(1)原式=﹣1+1﹣×4=﹣1+1﹣=0;
(2)原式=9﹣6+5+5﹣1=18﹣6.
21.解:(1)=;=
(2)
(3)
=,==10﹣1=9.
22.解:原式=2﹣+=.
23.解:(1)a===﹣2,b===+2.
a+b=﹣2++2=2,
(2)∵2<<3,
∴0<﹣2<1,4<+2<5,
∴m=﹣2,n=4,
∴4m2+4mn+n2=(2m+n)2=(2﹣4+4)2=20.
24.解:∵两个正方形木板的面积分别为18dm2和32dm2,
∴这两个正方形的边长分别为:=3(dm),=4(dm),
∴剩余木料的面积为:(4﹣3)×3=×3=6(dm2).
25.解:(1)∵a=﹣2020,
∴1﹣a=1﹣(﹣2020)=2021,
故小芳开方时,出现错误,
故答案为:小芳;
(2)错误的原因在于未能正确地运用二次根式的性质:=|a|,
故答案为:=|a|;
(3)a+2
=a+2,
∵a=﹣2019,
∴a﹣3<0,
∴原式=a+2(3﹣a)=a+6﹣2a=6﹣a=6﹣(﹣2019)=6+2019=2025,
即代数式a+2的值是2025.
1.下列计算正确的是( )
A.=
B.=×
C.4=3
D.=
2.若2<a<3,则等于( )
A.5﹣2a
B.1﹣2a
C.2a﹣5
D.2a﹣1
3.已知:a=,b=,则a与b的关系是( )
A.a﹣b=0
B.a+b=0
C.ab=1
D.a2=b2
4.计算(﹣3)2020(+3)2021的值为( )
A.1
B.+3
C.﹣3
D.3
5.若代数式有意义,则x的取值范围是( )
A.x>且x≠3
B.x≥
C.x≥且x≠3
D.x≤且x≠﹣3
6.下列根式中,与不是同类二次根式的是( )
A.
B.
C.
D.
7.把根号外的因式移入根号内得( )
A.
B.
C.
D.
8.下列各式中,一定是二次根式的个数为( )
,,,,,(a≥0),(a<)
A.3个
B.4个
C.5个
D.6个
9.在、、、、中,最简二次根式有( )
A.1个
B.2个
C.3个
D.4个
10.若式子有意义,则实数x的取值范围是
.
11.﹣=
.
12.=2,=3,=4,…观察下列各式:请你找出其中规律,并将第n(n≥1)个等式写出来
.
13.计算的结果为
.
14.已知0<a<1,化简=
.
15.若的值是整数,则自然数x的值为
.
16.若代数式有意义,则x的取值范围是
17.已知a,b在数轴上的位置如图,化简:=
.
18.不等式x﹣>0的解集是
.
19.若一直角三角形两直角边的长分别为,,则这个直角三角形斜边上的中线为
.
20.计算:
(1);
(2).
21.观察下列一组式的变形过程,然后回答问题:
例1:,
例2:,,
(1)=
;=
(2)请你用含n(n为正整数)的关系式表示上述各式子的变形规律.
(3)利用上面的结论,求下列式子的值..
22.计算:.
23.已知a=,b=.
(1)求a+b的值;
(2)设m是a小数部分,n是b整数部分,求代数式4m2+4mn+n2的值.
24.有一块矩形木块,木工采用如图方式,求木板上截出两个面积分别为18dm2和32dm2的正方形木板,求剩余木料的面积.
25.求代数式a+的值,其中a=﹣2020.
如图是小亮和小芳的解答过程.
(1)
的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质:
;
(3)求代数式a+2的值,其中a=﹣2019.
参考答案
1.解:A、+,无法计算,故此选项错误;
B、=×,故此选项错误;
C、4﹣=3,故此选项错误;
D、?=,故此选项正确.故选:D.
2.解:∵2<a<3,
∴=a﹣2﹣(3﹣a)=a﹣2﹣3+a=2a﹣5.故选:C.
3.解:分母有理化,可得a=2+,b=2﹣,
∴a﹣b=(2+)﹣(2﹣)=2,故A选项错误;
a+b=(2+)+(2﹣)=4,故B选项错误;
ab=(2+)×(2﹣)=4﹣3=1,故C选项正确;
∵a2=(2+)2=4+4+3=7+4,b2=(2﹣)2=4﹣4+3=7﹣4,
∴a2≠b2,故D选项错误;故选:C.
4.解:原式=(﹣3)2018(+3)2018×(+3)
=[(﹣3)(+3)]2018×(+3)
=(10﹣9)2018×(+3)=1×(+3)=+3,故选:B.
5.解:∵代数式有意义,
∴3x﹣2≥0,|x|﹣3≠0,
解得:x≥且x≠3.故选:C.
6.解:A、,与是同类二次根式;
B、,与是同类二次根式;
C、,与是同类二次根式;
D、与不是同类二次根式,故选:D.
7.解:∵成立,
∴﹣>0,即m<0,
∴原式=﹣=﹣.
故选:D.
8.解:一定是二次根式;
当m<0时,不是二次根式;
对于任意的数x,x2+1>0,则一定是二次根式;
是三次方根,不是二次根式;
﹣m2﹣1<0,则不是二次根式;
是二次根式;
当a<时,2a+1可能小于0,不是二次根式.
故选:A.
9.解:在、、、、中,最简二次根式为、.
故选:B.
10.解:∵式子有意义,
∴x+1≥0,x≠0,
解得:x≥﹣1且x≠0.
故答案为:x≥﹣1且x≠0.
11.解:原式=3﹣2=,
故答案为:.
12.解:由=2,=3,=4,…得
=(n+1),
故答案为:=(n+1).
13.解:原式=3﹣2=.
故答案为:.
14.解:∵0<a<1,
∴<,
∴原式=﹣
=﹣
=﹣()=2.
15.解:由题意得:x≤17,
当x=0时,原式=,不合题意;
当x=1时,原式==4;
当x=2时,原式=,不合题意;
当x=3时,原式=,不合题意;
当x=4时,原式=,不合题意;
当x=5时,原式==2,不合题意;
当x=6时,原式=,不合题意;
当x=7时,原式=,不合题意;
当x=8时,原式==3;
当x=9时,原式==2,不合题意;
当x=10时,原式=,不合题意;
当x=11时,原式=,不合题意;
当x=12时,原式=,不合题意;
当x=13时,原式==2;
当x=14时,原式=,不合题意;
当x=15时,原式=,不合题意;
当x=16时,原式=1;
当x=17时,原式=0.
综上所述,x=1、8、13、16或17.
16.解:若代数式有意义,
必有
解得﹣3≤x<且x≠﹣2.
17.解:由a,b在数轴上的位置可知:﹣2<a<﹣1,2<b<3,
∴=﹣(a+1)+2﹣b=1﹣a﹣b.
18.解:x﹣>0
,
故答案为:x.
19.解:∵一直角三角形两直角边的长分别为,,
∴斜边长为:=2,
∴这个直角三角形斜边上的中线为,
故答案为:.
20.解:(1)原式=﹣1+1﹣×4=﹣1+1﹣=0;
(2)原式=9﹣6+5+5﹣1=18﹣6.
21.解:(1)=;=
(2)
(3)
=,==10﹣1=9.
22.解:原式=2﹣+=.
23.解:(1)a===﹣2,b===+2.
a+b=﹣2++2=2,
(2)∵2<<3,
∴0<﹣2<1,4<+2<5,
∴m=﹣2,n=4,
∴4m2+4mn+n2=(2m+n)2=(2﹣4+4)2=20.
24.解:∵两个正方形木板的面积分别为18dm2和32dm2,
∴这两个正方形的边长分别为:=3(dm),=4(dm),
∴剩余木料的面积为:(4﹣3)×3=×3=6(dm2).
25.解:(1)∵a=﹣2020,
∴1﹣a=1﹣(﹣2020)=2021,
故小芳开方时,出现错误,
故答案为:小芳;
(2)错误的原因在于未能正确地运用二次根式的性质:=|a|,
故答案为:=|a|;
(3)a+2
=a+2,
∵a=﹣2019,
∴a﹣3<0,
∴原式=a+2(3﹣a)=a+6﹣2a=6﹣a=6﹣(﹣2019)=6+2019=2025,
即代数式a+2的值是2025.
