2020-2021学年人教版八年级下册第十九章一次函数与动点最值问题学案(word版试题无答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册第十九章一次函数与动点最值问题学案(word版试题无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 352.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 14:31:06 | ||
图片预览




文档简介
一次函数提优综合——最值与数形结合
一次函数与动点最值问题
知识导航
1.关于x的一次函数y=k(x-m)+n或y=kx-km+n一定过定点(m,n).
2.直线外一点与直线上各点的连线中,垂线段最短.
3.利用三角形两边之和大于第三边,两边之差小于第三边求最值.
4.利用平方数,绝对值,算术平方根的非负性求最值.
【板块一】过定点的直线
题型一
定点动直线
【例1】(1)一次函数y=kx一定经过点_________;若一次函数的图象经过原点,那么该一次函数的解析式可设为_________.
(2)一次函数y=kx+2一定经过点_________;若一次函数的图象经过点(0,-4),那么该一次函数的解析式可设为_________;
(3)一次函数y=kx-2k+1一定经过点_________;若一次函数的图象经过点(-2,4),该一次函数的解析式可设为_________.
题型二
动点定直线
【例2】利用坐标判断点在定直线上.
(1)点P(m,m+2)一定在直线_________上;
(2)点P(m+1,2m-3)一定在直线_________上.
针对练习1
1.过定点的动直线的应用:
已知一次函数y=2kx-k+2.
(1)其图象过定点_________;
(2)直线y=2kx-k+2和直线y=4x的交点是_________;
(3)若0<k<2,不等式2kx-k+2≤4x的解集是_________;
(4)当x=1时,y<0,则k的取值范围是_________;
(5)若A(,3),B(4,-3),该一次函数的图象与线段AB有交点,则k的取值范围是_________.
2.动点在定直线上的应用:
直线AB:y=2x+4交x轴于点A,交y轴于点B,C(1,0),点P为直线AB上一点,将线段PC绕点C顺时针旋转90°,得CQ.
(1)若点P横坐标为-1时,求点Q坐标;
(2)若点P横坐标为m,试用含m的式子表示点Q的坐标;
(3)当点P在直线AB上运动时,则点Q总在直线l上运动,求直线l的解析式.
【板块二】直线型动点最值问题
题型三
点到直线的距离最短
方法技巧
利用垂线段最短,可求定点到直线型动点的最小值问题.
【例1】点P是x轴上一点,A(0,4),将线段PA绕点A逆时针旋转90°得到线段AQ,求OQ的最小值.
【例2】如图,A(4,0),△OAB为等边三角形,点C为x轴上一动点,以BC为边在直线BC的右侧作等边△BCD,连接OD.
(1)点D在某一确定的函数图象上运动,其解析式为_________;
(2)OD的最小值为_________.
题型四
两线段或多线段的和差最值问题
方法技巧
利用两边之和大于第三边,两边之差小于第三边,求两线段或多线段的和差最大值或最小值;在平面直角坐标系中,常作一个定点的对称点,然后连接这一对称点与另一定点,求最值.这一方法也叫化折为直.
【例3】如图,A(-4,2),B(-1,1),在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.
【例4】如图,A(-4,2),B(-1,1),在x轴上找一点P,使|PA-PB|的值最大,并求此时点P的坐标.
针对练习2
1.一次函数y=k(x-1)+3k-4的图象与x轴交于点A,与y轴交于点B,则点O到该直线的距离的最大值是_________;
2.如图,B(0,3),点A为x轴上一动点,将线段AB绕点A顺时针旋转90°得线段AC,连接OC.
(1)设A(a,0),用含a的式子表示点C坐标_________;
(2)点C在某一确定的函数图象上运动,其解析式为_________;
(3)OC长度的最小值为_________.
3.如图,A(0,2),点B为x轴上一动点,将线段AB绕点A逆时针旋转60°,得线段AC,线段OC的最小值是_________.
第2题
第3题
第4题
第5题
4.如图,在△ABC中,∠ACB=90°,AC=BC=4,点M为AB的中点,点D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ME,点D在运动的过程中,ME的最小值为(
)
A.2
B.2
C.4
D.4
5.如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE的最小值为_________.
6.如图,直线y=x+4与坐标轴交于点A,B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.
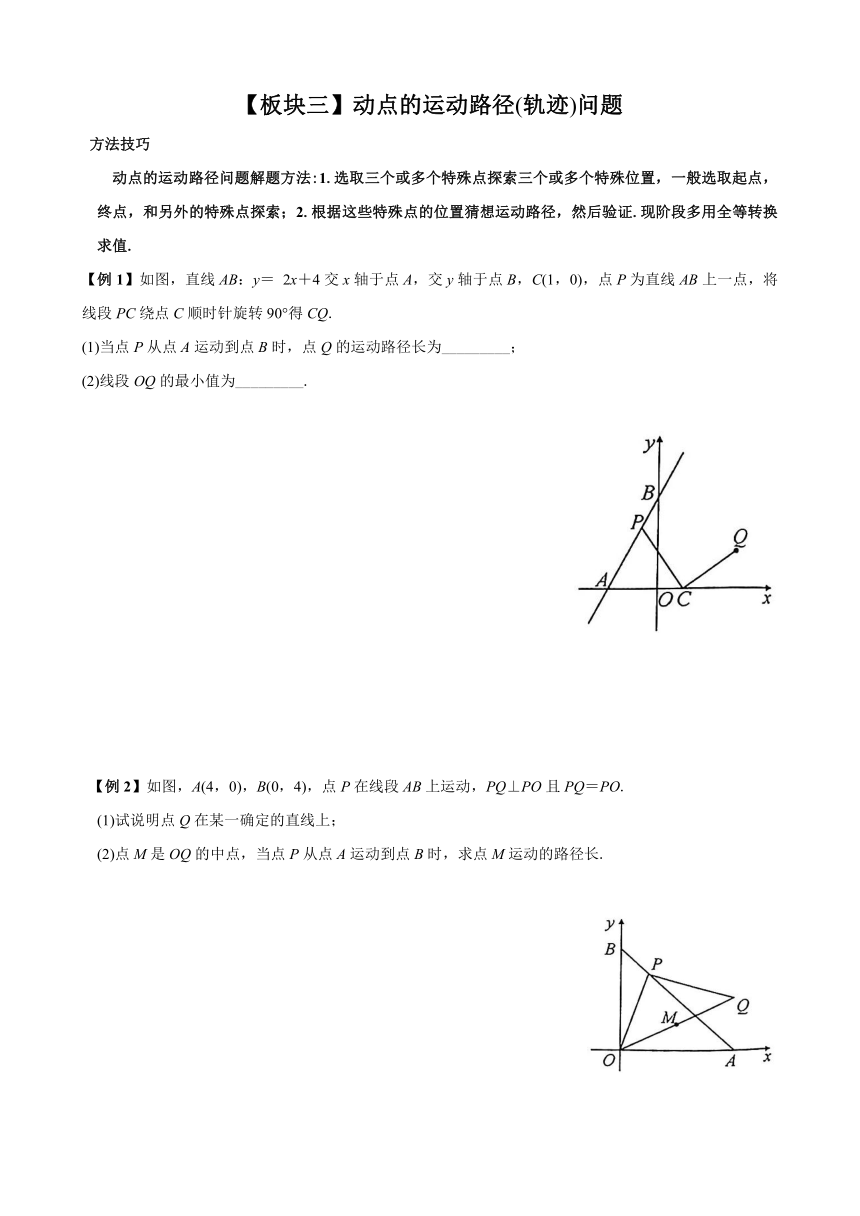
【板块三】动点的运动路径(轨迹)问题
方法技巧
动点的运动路径问题解题方法:1.选取三个或多个特殊点探索三个或多个特殊位置,一般选取起点,终点,和另外的特殊点探索;2.根据这些特殊点的位置猜想运动路径,然后验证.现阶段多用全等转换求值.
【例1】如图,直线AB:y=
2x+4交x轴于点A,交y轴于点B,C(1,0),点P为直线AB上一点,将线段PC绕点C顺时针旋转90°得CQ.
(1)当点P从点A运动到点B时,点Q的运动路径长为_________;
(2)线段OQ的最小值为_________.
【例2】如图,A(4,0),B(0,4),点P在线段AB上运动,PQ⊥PO且PQ=PO.
(1)试说明点Q在某一确定的直线上;
(2)点M是OQ的中点,当点P从点A运动到点B时,求点M运动的路径长.
针对练习3
1.在平面直角坐标系中,A(0,4),点B沿着某条路径运动,以点B为旋转中心,将点A逆时针旋转60°到点C(m,2).若-5≤m≤5,则点B运动的路径长为_________.
2.在平面直角坐标系中,已知点A(a,0),C(0,b),且a,b满足(a+1)2+=0.
(1)直接写出:a=_________,b=_________;
(2)如图1,点B为x轴正半轴上的一点,BE⊥AC于点E,交y轴于点D,连接OE.若OE平分∠AEB,求直线BE的解析式;
(3)如图2,在(2)的条件下,点M为直线BE上的一动点,连接OM,将线段OM绕点M逆时针旋转90°,点O的对应点为N,当点M运动时,判断点N的运动路线是什么图形,并说明理由.
图1
图2
3.如图1,直线y=-x+3分别与y轴、x轴交于点A,B,点C的坐标为(-3,0),点D为直线AB上的一动点,连接CD交y轴于点E.
(1)点B的坐标为_________,不等式-x+3>0的解集为_________;
(2)若S△COE=S△ADE,求点D的坐标;
(3)如图2,以CD为边作菱形CDFG,且∠CDF=60°,当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.
图1
图2
一次函数大综合——数形结合
1.已知点A(a,3),点B(b,6),点C(5,c),AC⊥x轴,CB⊥y轴,点B在第二象限且到两坐标轴的距离相等.
(1)写出A,B,C三点的坐标;
(2)求△ABC的面积;
(3)若点P为线段OB上的动点,当△BCP面积大于12小于16时,求点P的横坐标的取值范围.
2.
在平面直角坐标系中,A(a,b),B(c,d),且+|b-d-6|=0.
(1)直接写出a与c,b与d的关系式;
(2)如果b=c=0,点P(m,m+6),且m>0,S△PAB=4S△AOB,求点P的坐标;
(3)如果b=3,连接AB交x轴于点Q.
①直接写出点Q的坐标(用含a的式子表示);
②若S△AOB≤24,求a的取值范围.
3.
(2019黄陂区期末)如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴于点B.AC⊥y轴于点C,点A(4a,3a),且四边形ABOC的面积为48.
(1)如图1,直接写出点A的坐标为_________;
(2)如图2,点D从点O出发以每秒1个单位长度的速度沿y轴正半轴运动,同时,点E从点A出发,以每秒2个单位长度的速度沿射线BA运动,DE交线段AC于点F,设运动的时间为t秒,当S△AEF<S△CDF时,求t的取值范围;
(3)如图3,将线段BC平移,使点B的对应点M恰好落在y轴负半轴上,点C的对应点为N,连接BN交y轴轴于点P,当OM=3OP时,求点M的坐标.
4.
在平面直角坐标系中,已知点A(a,0),B(a,6),C(a-2,2).
(1)若a=2,则△ABC的面积为_________;
(2)将线段BC向右平移m个单位,若△ABC的面积小于4,求m的取值范围;
(3)若点D(a+8,8),连结AD,将线段BC向右平移n个单位,若线段BC与线段AD有公共点,请直接写出n的取值范围_________.
5.在平面直角坐标系中,点A(a,b),B(c,d),且+|b-d-4|=0.
(1)如果a=-1,b=-3,求A,B两点的坐标;
(2)如果a=-1,b=-3,求直线AB与x轴的交点M以及与y轴的交点N的坐标;
(3)如果点A在x轴上方平行于x轴,且在到x轴距离等于2的直线上运动,若△ABO的面积不超过21,求a的取值范围.
6.如图,在平面直角坐标系中,直线l交x轴于点A,交y轴于点B,下表列举的是直线l上的点P(x,y)的取值情况:
(1)直线l上的点P(x,y)的横、纵坐标之间的数量关系是_________(直接写出结果);
(2)若点P(-2,2),点Q(q,0),若以P,Q,O,B为顶点的四边形的面积大于5,求q的取值范围;
(3)已知坐标平面内第一象限的点M(m,n),N(m+4,n+4),若△PMN的面积是12,求m,n的数量关系.
一次函数与动点最值问题
知识导航
1.关于x的一次函数y=k(x-m)+n或y=kx-km+n一定过定点(m,n).
2.直线外一点与直线上各点的连线中,垂线段最短.
3.利用三角形两边之和大于第三边,两边之差小于第三边求最值.
4.利用平方数,绝对值,算术平方根的非负性求最值.
【板块一】过定点的直线
题型一
定点动直线
【例1】(1)一次函数y=kx一定经过点_________;若一次函数的图象经过原点,那么该一次函数的解析式可设为_________.
(2)一次函数y=kx+2一定经过点_________;若一次函数的图象经过点(0,-4),那么该一次函数的解析式可设为_________;
(3)一次函数y=kx-2k+1一定经过点_________;若一次函数的图象经过点(-2,4),该一次函数的解析式可设为_________.
题型二
动点定直线
【例2】利用坐标判断点在定直线上.
(1)点P(m,m+2)一定在直线_________上;
(2)点P(m+1,2m-3)一定在直线_________上.
针对练习1
1.过定点的动直线的应用:
已知一次函数y=2kx-k+2.
(1)其图象过定点_________;
(2)直线y=2kx-k+2和直线y=4x的交点是_________;
(3)若0<k<2,不等式2kx-k+2≤4x的解集是_________;
(4)当x=1时,y<0,则k的取值范围是_________;
(5)若A(,3),B(4,-3),该一次函数的图象与线段AB有交点,则k的取值范围是_________.
2.动点在定直线上的应用:
直线AB:y=2x+4交x轴于点A,交y轴于点B,C(1,0),点P为直线AB上一点,将线段PC绕点C顺时针旋转90°,得CQ.
(1)若点P横坐标为-1时,求点Q坐标;
(2)若点P横坐标为m,试用含m的式子表示点Q的坐标;
(3)当点P在直线AB上运动时,则点Q总在直线l上运动,求直线l的解析式.
【板块二】直线型动点最值问题
题型三
点到直线的距离最短
方法技巧
利用垂线段最短,可求定点到直线型动点的最小值问题.
【例1】点P是x轴上一点,A(0,4),将线段PA绕点A逆时针旋转90°得到线段AQ,求OQ的最小值.
【例2】如图,A(4,0),△OAB为等边三角形,点C为x轴上一动点,以BC为边在直线BC的右侧作等边△BCD,连接OD.
(1)点D在某一确定的函数图象上运动,其解析式为_________;
(2)OD的最小值为_________.
题型四
两线段或多线段的和差最值问题
方法技巧
利用两边之和大于第三边,两边之差小于第三边,求两线段或多线段的和差最大值或最小值;在平面直角坐标系中,常作一个定点的对称点,然后连接这一对称点与另一定点,求最值.这一方法也叫化折为直.
【例3】如图,A(-4,2),B(-1,1),在x轴上找一点P,使△PAB的周长最小,求这个最小值及点P的坐标.
【例4】如图,A(-4,2),B(-1,1),在x轴上找一点P,使|PA-PB|的值最大,并求此时点P的坐标.
针对练习2
1.一次函数y=k(x-1)+3k-4的图象与x轴交于点A,与y轴交于点B,则点O到该直线的距离的最大值是_________;
2.如图,B(0,3),点A为x轴上一动点,将线段AB绕点A顺时针旋转90°得线段AC,连接OC.
(1)设A(a,0),用含a的式子表示点C坐标_________;
(2)点C在某一确定的函数图象上运动,其解析式为_________;
(3)OC长度的最小值为_________.
3.如图,A(0,2),点B为x轴上一动点,将线段AB绕点A逆时针旋转60°,得线段AC,线段OC的最小值是_________.
第2题
第3题
第4题
第5题
4.如图,在△ABC中,∠ACB=90°,AC=BC=4,点M为AB的中点,点D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ME,点D在运动的过程中,ME的最小值为(
)
A.2
B.2
C.4
D.4
5.如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE的最小值为_________.
6.如图,直线y=x+4与坐标轴交于点A,B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.
【板块三】动点的运动路径(轨迹)问题
方法技巧
动点的运动路径问题解题方法:1.选取三个或多个特殊点探索三个或多个特殊位置,一般选取起点,终点,和另外的特殊点探索;2.根据这些特殊点的位置猜想运动路径,然后验证.现阶段多用全等转换求值.
【例1】如图,直线AB:y=
2x+4交x轴于点A,交y轴于点B,C(1,0),点P为直线AB上一点,将线段PC绕点C顺时针旋转90°得CQ.
(1)当点P从点A运动到点B时,点Q的运动路径长为_________;
(2)线段OQ的最小值为_________.
【例2】如图,A(4,0),B(0,4),点P在线段AB上运动,PQ⊥PO且PQ=PO.
(1)试说明点Q在某一确定的直线上;
(2)点M是OQ的中点,当点P从点A运动到点B时,求点M运动的路径长.
针对练习3
1.在平面直角坐标系中,A(0,4),点B沿着某条路径运动,以点B为旋转中心,将点A逆时针旋转60°到点C(m,2).若-5≤m≤5,则点B运动的路径长为_________.
2.在平面直角坐标系中,已知点A(a,0),C(0,b),且a,b满足(a+1)2+=0.
(1)直接写出:a=_________,b=_________;
(2)如图1,点B为x轴正半轴上的一点,BE⊥AC于点E,交y轴于点D,连接OE.若OE平分∠AEB,求直线BE的解析式;
(3)如图2,在(2)的条件下,点M为直线BE上的一动点,连接OM,将线段OM绕点M逆时针旋转90°,点O的对应点为N,当点M运动时,判断点N的运动路线是什么图形,并说明理由.
图1
图2
3.如图1,直线y=-x+3分别与y轴、x轴交于点A,B,点C的坐标为(-3,0),点D为直线AB上的一动点,连接CD交y轴于点E.
(1)点B的坐标为_________,不等式-x+3>0的解集为_________;
(2)若S△COE=S△ADE,求点D的坐标;
(3)如图2,以CD为边作菱形CDFG,且∠CDF=60°,当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.
图1
图2
一次函数大综合——数形结合
1.已知点A(a,3),点B(b,6),点C(5,c),AC⊥x轴,CB⊥y轴,点B在第二象限且到两坐标轴的距离相等.
(1)写出A,B,C三点的坐标;
(2)求△ABC的面积;
(3)若点P为线段OB上的动点,当△BCP面积大于12小于16时,求点P的横坐标的取值范围.
2.
在平面直角坐标系中,A(a,b),B(c,d),且+|b-d-6|=0.
(1)直接写出a与c,b与d的关系式;
(2)如果b=c=0,点P(m,m+6),且m>0,S△PAB=4S△AOB,求点P的坐标;
(3)如果b=3,连接AB交x轴于点Q.
①直接写出点Q的坐标(用含a的式子表示);
②若S△AOB≤24,求a的取值范围.
3.
(2019黄陂区期末)如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴于点B.AC⊥y轴于点C,点A(4a,3a),且四边形ABOC的面积为48.
(1)如图1,直接写出点A的坐标为_________;
(2)如图2,点D从点O出发以每秒1个单位长度的速度沿y轴正半轴运动,同时,点E从点A出发,以每秒2个单位长度的速度沿射线BA运动,DE交线段AC于点F,设运动的时间为t秒,当S△AEF<S△CDF时,求t的取值范围;
(3)如图3,将线段BC平移,使点B的对应点M恰好落在y轴负半轴上,点C的对应点为N,连接BN交y轴轴于点P,当OM=3OP时,求点M的坐标.
4.
在平面直角坐标系中,已知点A(a,0),B(a,6),C(a-2,2).
(1)若a=2,则△ABC的面积为_________;
(2)将线段BC向右平移m个单位,若△ABC的面积小于4,求m的取值范围;
(3)若点D(a+8,8),连结AD,将线段BC向右平移n个单位,若线段BC与线段AD有公共点,请直接写出n的取值范围_________.
5.在平面直角坐标系中,点A(a,b),B(c,d),且+|b-d-4|=0.
(1)如果a=-1,b=-3,求A,B两点的坐标;
(2)如果a=-1,b=-3,求直线AB与x轴的交点M以及与y轴的交点N的坐标;
(3)如果点A在x轴上方平行于x轴,且在到x轴距离等于2的直线上运动,若△ABO的面积不超过21,求a的取值范围.
6.如图,在平面直角坐标系中,直线l交x轴于点A,交y轴于点B,下表列举的是直线l上的点P(x,y)的取值情况:
(1)直线l上的点P(x,y)的横、纵坐标之间的数量关系是_________(直接写出结果);
(2)若点P(-2,2),点Q(q,0),若以P,Q,O,B为顶点的四边形的面积大于5,求q的取值范围;
(3)已知坐标平面内第一象限的点M(m,n),N(m+4,n+4),若△PMN的面积是12,求m,n的数量关系.
