全等三角形复习(1)
图片预览




文档简介
(共27张PPT)
全等三角形的复习(一)
复 习 课
新余四中 付伟华
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
想一想
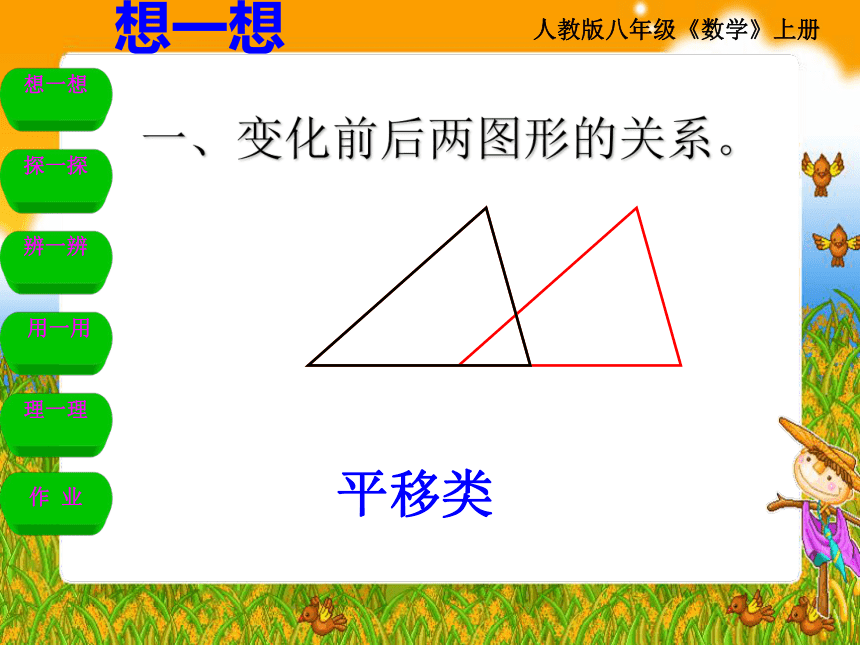
平移类
一、变化前后两图形的关系。
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
想一想
A
B
C
E
P
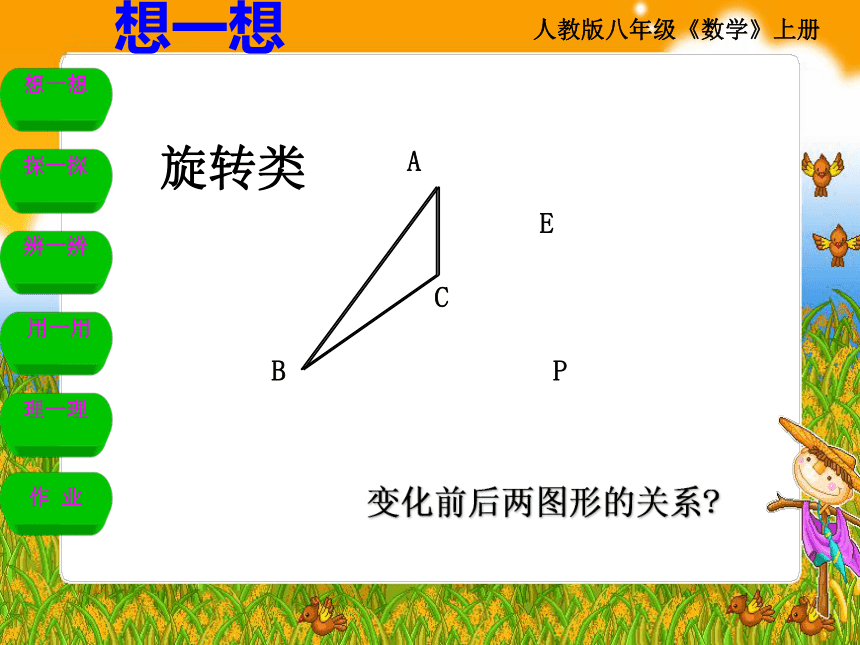
旋转类
变化前后两图形的关系
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
想一想
变化前后两图形的关系
翻折类
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
1、全等三角形的定义:
能够完全重合的两个三角形叫做
全等三角形。
2、全等三角形的性质:
全等三角形的对应边相等;
全等三角形的对应角相等;
探一探
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
探一探
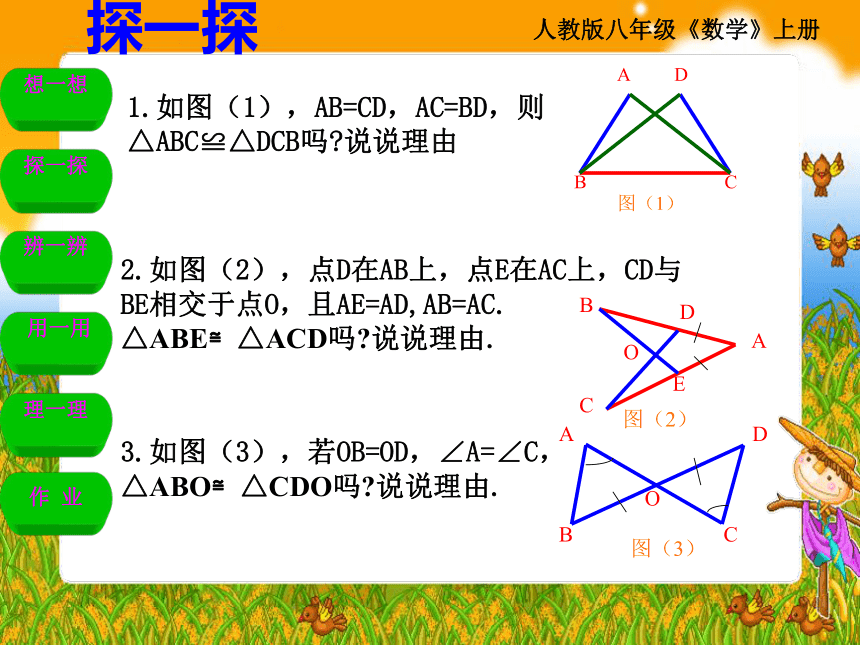
1.如图(1),AB=CD,AC=BD,则△ABC≌△DCB吗 说说理由
A
D
B
C
图(1)
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AE=AD,AB=AC. △ABE≌△ACD吗 说说理由.
B
C
O
D
E
A
图(2)
3.如图(3),若OB=OD,∠A=∠C, △ABO≌△CDO吗 说说理由.
A
D
B
C
O
图(3)
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
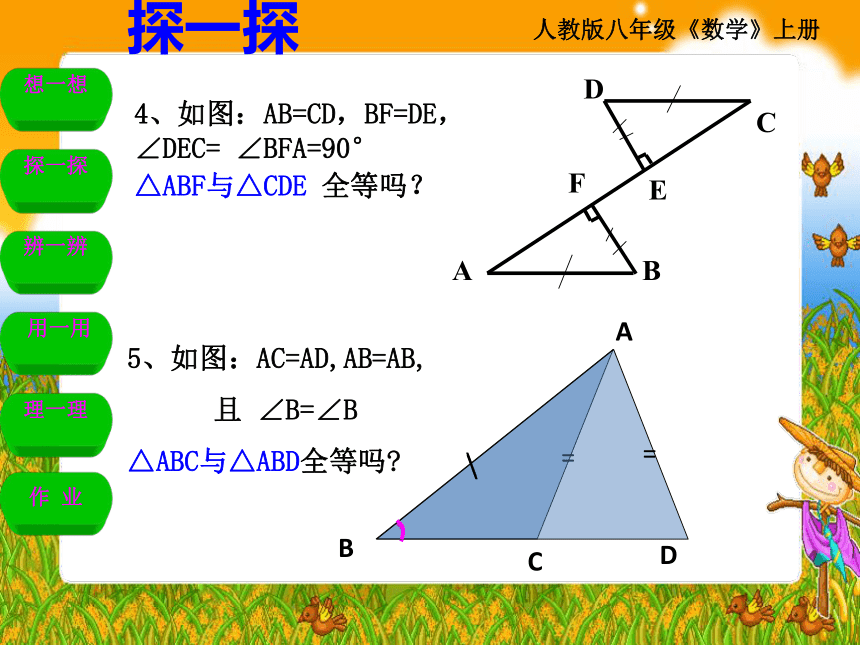
5、如图:AC=AD,AB=AB,
且 ∠B=∠B
△ABC与△ABD全等吗
\
=
\
=
A
B
C
D
4、如图:AB=CD,BF=DE,
∠DEC= ∠BFA=90°
△ABF与△CDE 全等吗?
探一探
C
D
E
A
B
F
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
①一般三角形全等的条件:
SAS、ASA、AAS、SSS
②直角三角形全等的条件:
SAS、ASA、AAS、SSS、HL
探一探
人教版八年级《数学》上册
辨一辨
想一想
探一探
辨一辨
用一用
理一理
作 业
A
B
E
C
D
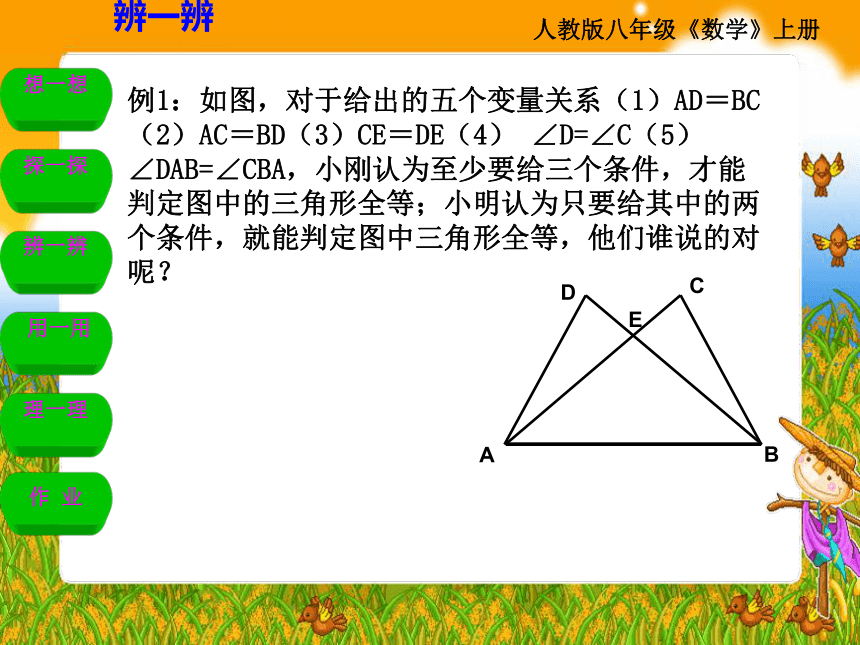
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
人教版八年级《数学》上册
辨一辨
A
B
E
C
D
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
人教版八年级《数学》上册
辨一辨
A
B
E
C
D
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
AD=BC
AC=BD
AB=BA
△ABD≌△BAC(SSS)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
AD=BC
DE=CE
SSA不可以判定全等。
∠1=∠2
A
B
E
C
D
1
2
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
AD=BC
∠D=∠C
∠1=∠2
△ADE≌△BCE(AAS)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
AD=BC
∠DAB=∠CBA
AB=BA
△ABD≌△BAC(SAS)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
∵AC=BD
∴AE=BE
DE=CE
DE=CE
∠1=∠2
AE=BE
△ADE≌△BCE(SAS)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
AC=BD
∠D=∠C
SSA不可以判定全等。
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
AC=BD
∠DAB=∠CBA
SSA不可以判定全等。
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
∠D=∠C
∠1=∠2
DE=CE
△ADE≌△BCE(ASA)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
DE=CE
∠DAB=∠CBA
没有形成全等的条件
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
∠D=∠C
∠DAB=∠CBA
AB=BA
△ABD≌△BAC(AAS)
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
例2. 如图,CA=CB,AD=BD,那么
∠A=∠B吗?请说明理由。
添加辅助线:构造全等三角形
变一变
A
C
D
B
∠A=∠B
解:
理由如下:
连结DC,
在△ACD和△BCD中
CA=CB
AD=BD
CD=CD
∴ △ACD≌△BCD(SSS)
∴ ∠A=∠B
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
例3. 如图,CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN。
变一变
A
C
D
B
M
N
证明:连结CD
在△ACD和△BCD中
CA=CB
AD=BD
CD=CD
∴ △ACD≌△BCD(SSS)
∴ ∠A=∠B
∵M、N分别是CA、CB的中点,AC=BC
∴ AM=BN
在△AMD和△BND中
AM=BN
∠A=∠B
AD=BD
∴ △AMD≌△BND(SAS)
∴ DM=DN。
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
1、如图:两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。
12米
12米
用一用
解:两个木桩离旗杆底部的距离相等
理由如下:
∵AD⊥BC ∴∠ADB=∠ADC=90°,
在Rt△ADB 和Rt△ADC中
AB=AC=12
AD=AD
∴Rt△ADB ≌Rt△ADC(HL)
∴ BD=CD
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
一、全等三角形的定义、性质、判定。
二、平移、旋转、翻折都是全等变换。
三、全等是证明线段相等、角相等的
重要方法.
理一理
作业一:
P64 6、12、14
作业二:如图,在△ABC中, ∠ C=90°,AD 平分 ∠CAB,BC=8,BD=5,问:点D到AB的距离是多少?
D
A
B
C
E
5
请用三角形全等的知识自行设计一种测量底
部不可到达物体的宽度(如河宽、池塘宽、山底部
宽等等)的方案。
作业三
谢谢!
全等三角形的复习(一)
复 习 课
新余四中 付伟华
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
想一想
平移类
一、变化前后两图形的关系。
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
想一想
A
B
C
E
P
旋转类
变化前后两图形的关系
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
想一想
变化前后两图形的关系
翻折类
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
1、全等三角形的定义:
能够完全重合的两个三角形叫做
全等三角形。
2、全等三角形的性质:
全等三角形的对应边相等;
全等三角形的对应角相等;
探一探
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
探一探
1.如图(1),AB=CD,AC=BD,则△ABC≌△DCB吗 说说理由
A
D
B
C
图(1)
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AE=AD,AB=AC. △ABE≌△ACD吗 说说理由.
B
C
O
D
E
A
图(2)
3.如图(3),若OB=OD,∠A=∠C, △ABO≌△CDO吗 说说理由.
A
D
B
C
O
图(3)
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
5、如图:AC=AD,AB=AB,
且 ∠B=∠B
△ABC与△ABD全等吗
\
=
\
=
A
B
C
D
4、如图:AB=CD,BF=DE,
∠DEC= ∠BFA=90°
△ABF与△CDE 全等吗?
探一探
C
D
E
A
B
F
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
①一般三角形全等的条件:
SAS、ASA、AAS、SSS
②直角三角形全等的条件:
SAS、ASA、AAS、SSS、HL
探一探
人教版八年级《数学》上册
辨一辨
想一想
探一探
辨一辨
用一用
理一理
作 业
A
B
E
C
D
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
人教版八年级《数学》上册
辨一辨
A
B
E
C
D
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
人教版八年级《数学》上册
辨一辨
A
B
E
C
D
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
AD=BC
AC=BD
AB=BA
△ABD≌△BAC(SSS)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
AD=BC
DE=CE
SSA不可以判定全等。
∠1=∠2
A
B
E
C
D
1
2
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
AD=BC
∠D=∠C
∠1=∠2
△ADE≌△BCE(AAS)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
AD=BC
∠DAB=∠CBA
AB=BA
△ABD≌△BAC(SAS)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
∵AC=BD
∴AE=BE
DE=CE
DE=CE
∠1=∠2
AE=BE
△ADE≌△BCE(SAS)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
AC=BD
∠D=∠C
SSA不可以判定全等。
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
AC=BD
∠DAB=∠CBA
SSA不可以判定全等。
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
∠D=∠C
∠1=∠2
DE=CE
△ADE≌△BCE(ASA)
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)DE=CE (4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
DE=CE
∠DAB=∠CBA
没有形成全等的条件
人教版八年级《数学》上册
辨一辨
例1:如图,对于给出的五个变量关系(1)AD=BC(2)AC=BD(3)CE=DE(4) ∠D=∠C(5)∠DAB=∠CBA,小刚认为至少要给三个条件,才能判定图中的三角形全等;小明认为只要给其中的两个条件,就能判定图中三角形全等,他们谁说的对呢?
(1)(2)
(1)(3)
(1)(4)
(1)(5)
(2)(3)
(2)(4)
(2)(5)
(3)(4)
(3)(5)
(4)(5)
A
B
E
C
D
1
2
∠D=∠C
∠DAB=∠CBA
AB=BA
△ABD≌△BAC(AAS)
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
例2. 如图,CA=CB,AD=BD,那么
∠A=∠B吗?请说明理由。
添加辅助线:构造全等三角形
变一变
A
C
D
B
∠A=∠B
解:
理由如下:
连结DC,
在△ACD和△BCD中
CA=CB
AD=BD
CD=CD
∴ △ACD≌△BCD(SSS)
∴ ∠A=∠B
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
例3. 如图,CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN。
变一变
A
C
D
B
M
N
证明:连结CD
在△ACD和△BCD中
CA=CB
AD=BD
CD=CD
∴ △ACD≌△BCD(SSS)
∴ ∠A=∠B
∵M、N分别是CA、CB的中点,AC=BC
∴ AM=BN
在△AMD和△BND中
AM=BN
∠A=∠B
AD=BD
∴ △AMD≌△BND(SAS)
∴ DM=DN。
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
1、如图:两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。
12米
12米
用一用
解:两个木桩离旗杆底部的距离相等
理由如下:
∵AD⊥BC ∴∠ADB=∠ADC=90°,
在Rt△ADB 和Rt△ADC中
AB=AC=12
AD=AD
∴Rt△ADB ≌Rt△ADC(HL)
∴ BD=CD
想一想
探一探
辨一辨
用一用
理一理
作 业
人教版八年级《数学》上册
一、全等三角形的定义、性质、判定。
二、平移、旋转、翻折都是全等变换。
三、全等是证明线段相等、角相等的
重要方法.
理一理
作业一:
P64 6、12、14
作业二:如图,在△ABC中, ∠ C=90°,AD 平分 ∠CAB,BC=8,BD=5,问:点D到AB的距离是多少?
D
A
B
C
E
5
请用三角形全等的知识自行设计一种测量底
部不可到达物体的宽度(如河宽、池塘宽、山底部
宽等等)的方案。
作业三
谢谢!
