2020-2021学年人教版八年级下册数学19.2一次函数同步提升训练题(word版含解析)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学19.2一次函数同步提升训练题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 14:34:49 | ||
图片预览



文档简介
2020-2021学年人教版八年级下册数学第19章19.2一次函数同步提升训练题
一、单选题
1.若函数是正比例函数,则的取值分别为(
)
A.
B.
C.
D.
2.下列函数①
y=x-6;②
y=;③
y=;④
y=7x中,y是x的一次函数的是
(
)
A.①②③
B.①③④
C.①②③④
D.②③④
3.已知直线与的交点的坐标为,则方程组的解是(
)
A.
B.
C.
D.
4.如图,直线经过点和点,直线过点A,则不等式的解集为(
)
A.
B.
C.
D.
5.若直线y=kx+b经过第一、二、四象限,则函数y=bx-k的大致图像是(
)
A.
B.
C.
D.
6.已知点在函数的图像上,则(
)
A.
B.
C.
D.
与的大小关系不能确定
7.下列关于一次函数的说法,错误的是(
)
A.函数图象与y轴的交点
B.当x值增大时,y随着x的增大而减小
C.当时,
D.图象经过第一、二、三象限
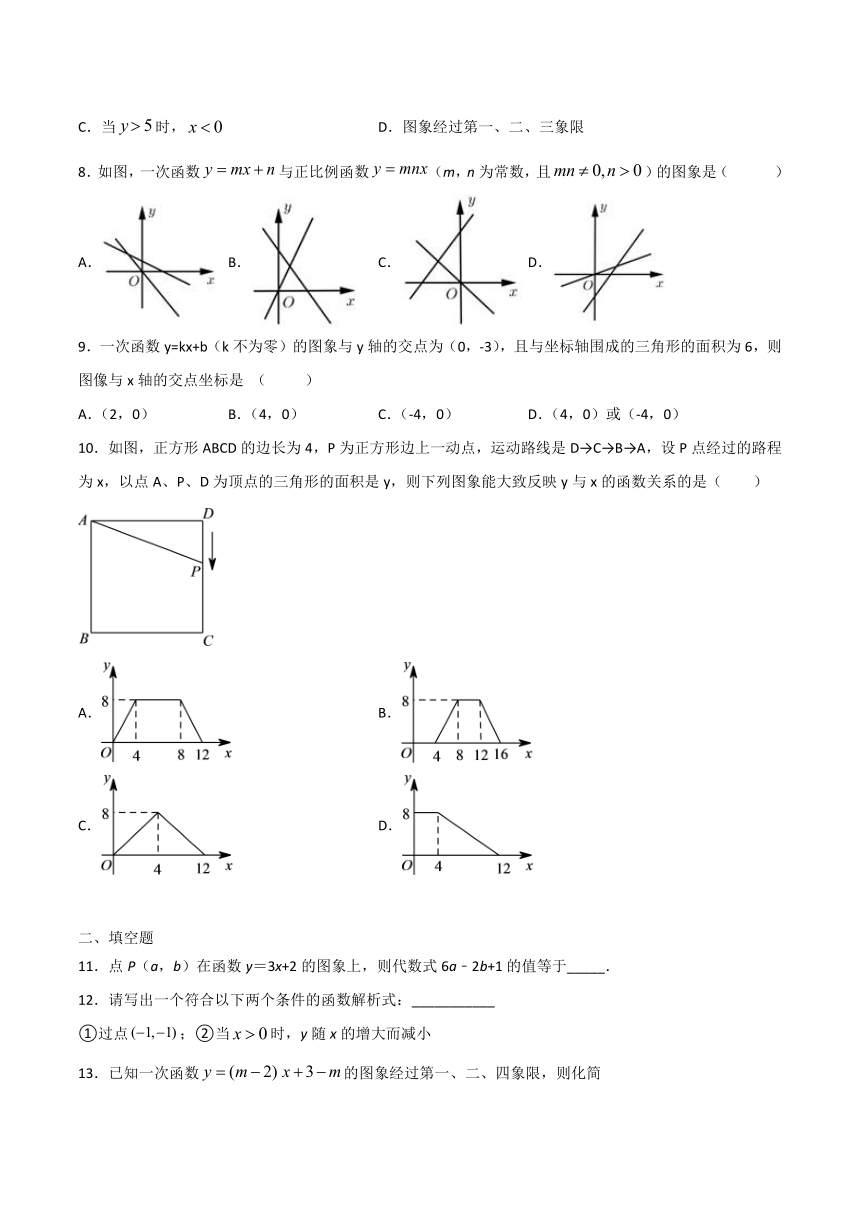
8.如图,一次函数与正比例函数(m,n为常数,且)的图象是( )
A.
B.
C.
D.
9.一次函数y=kx+b(k不为零)的图象与y轴的交点为(0,-3),且与坐标轴围成的三角形的面积为6,则图像与x轴的交点坐标是
(
)
A.(2,0)
B.(4,0)
C.(-4,0)
D.(4,0)或(-4,0)
10.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是(
)
A.
B.
C.
D.
二、填空题
11.点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于_____.
12.请写出一个符合以下两个条件的函数解析式:___________
①过点;②当时,y随x的增大而减小
13.已知一次函数的图象经过第一、二、四象限,则化简__________.
14.若,是一次函数图像上的不同的两个点,当时,,则a的取值范围是_________.
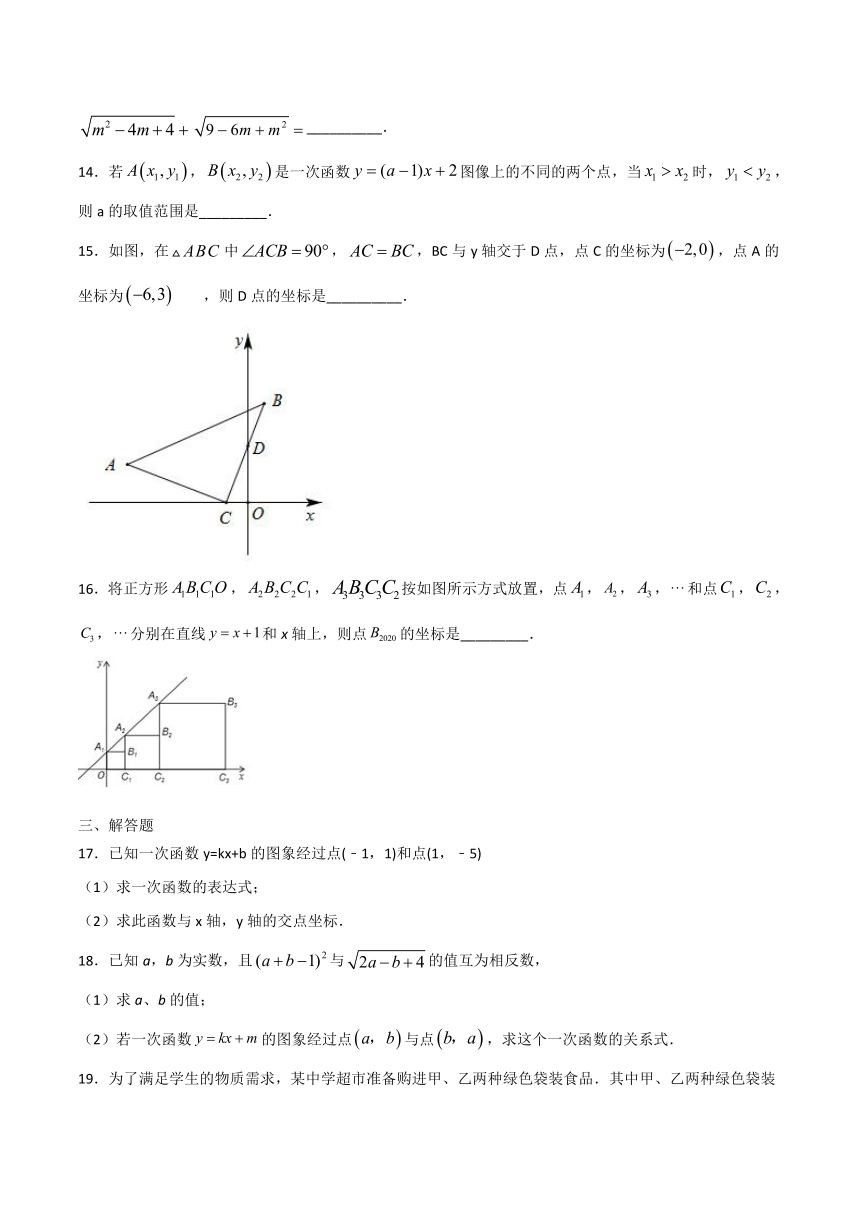
15.如图,在中,,BC与y轴交于D点,点C的坐标为,点A的坐标为,则D点的坐标是__________.
16.将正方形,,按如图所示方式放置,点,,,和点,,,分别在直线和x轴上,则点的坐标是_________.
三、解答题
17.已知一次函数y=kx+b的图象经过点(﹣1,1)和点(1,﹣5)
(1)求一次函数的表达式;
(2)求此函数与x轴,y轴的交点坐标.
18.已知a,b为实数,且与的值互为相反数,
(1)求a、b的值;
(2)若一次函数的图象经过点与点,求这个一次函数的关系式.
19.为了满足学生的物质需求,某中学超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
甲
乙
进价(元/袋)
m
售价(元/袋)
20
13
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求m的值.
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5230元,求该超市进货甲种绿色袋装食品的数量范围.
(3)在(2)的条件下,该超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
20.如图,直线与直线交于点.
(1)求点坐标;
(2)在轴上找一点使得最小,求的长;
(3)若为直线上一点,当面积为6时,求的坐标.
21.如图,在平面直角坐标系中,为坐标原点,点的坐标为,点的坐标为,点是直线上位于第二象限内的一个动点,过点作轴于点,记点关于轴的对称点为.设点的横坐标为.
(1)当时,
①求直线的表达式;
②若,求点的坐标;
(2)是否同时存在,,使得是等腰直角三角形?若存在,求出所有满足条件的,的值;若不存在,请说明理由.
22.操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.
(1)点P(1,2)经过T变换后得到的点Q的坐标为
;点P(a,b)经过T变换后得到的点Q的坐标为
;若点M经过T变换后得到点N(6,),则点M的坐标为
.
(2)点A(2,)是函数y=kx图象上的一点,经过T变换后得到点B.
①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求点D的坐标.
参考答案
1.A
解:∵函数是正比例函数,
∴,
解得:,
2.B
解:函数①y=x-6;③y=
;④y=7x,y是x的一次函数,
故选B.
3.A
将交点(1,a)代入两直线:
得:a=2,a=-1+b,
因此有a=2,b=a+1=3,
即交点为(1,2),
而交点就是两直线组成的方程组的解,
即方程组的解为.
故答案为:A.
4.B
由题意可得:直线y=kx+b与直线y=2x相交于点A,
∴不等式的解集为相当于直线y=2x在直线y=kx+b的下方所对应的x的取值范围和直线y=kx+b在x轴下方所对应的x的取值范围,
观察图象可知,当x<?1时,直线y=2x在直线y=kx+b的下方,当x>?2时,直线y=kx+b在x轴下方,
∴不等式的解集为:-2<
x<?1,
故选:B.
5.B
解:∵一次函数y=kx+b的图象经过第一、二、四象限,
∴k<0,b>0,
∴b>0,-k>0,
∴一次函数y=bx-k图象第一、二、三象限,
6.B
解:∵k=﹣9<0,
∴y随x的增大而减小,
∵﹣1<2,
∴y1>y2?,
7.D
A选项:,当时,则一次函数与y轴交于,A正确,故不符合题意;
B选项:,斜率,则,y随x增大而减小,B正确,故不符合题意;
C选项:,即,解得,C正确,故不符合题意;
D选项:,与y轴交于,与x轴交于,则图象过一、二、四象限,D错误,故符合题意.
8.A
A、由不过原点的一次函数图象得m<0,n>0,所以mn<0,则正比例函数图象过第二、四象限,所以A选项符合题意;
B、由不过原点的一次函数图象得m<0,n>0,所以mn<0,则正比例函数图象过第二、四象限,所以B选项不符合题意.
C、由不过原点的一次函数图象得m>0,n>0,所以mn>0,则正比例函数图象过第一、三象限,所以C选项不符合题意;
D、由不过原点的一次函数图象得m>0,n<0,所以mn<0,则正比例函数图象过第二、四象限,所以D选项不符合题意;
故选择:A.
9.D
解:把(0,-3)代入y=kx+b得b=-3,
把y=0代入y=kx-3得kx-3=0,解得:x=,
∵一次函数y=kx+b的图象与两坐标轴围成的三角形面积为6,
∴,解得:=±4
∴该函数图像与x轴的交点为(4,0)或(-4,0).
10.A
解:当点P由点D向点C运动,即0<x≤4时,y=AD?x=×4x=2x,y随x的增大而增大;
当点P在BC上运动,即4<x≤8时,y=×4×4=8,y是一个定值;
当点P在BA上运动,即8<x<12时,y=AD?(12-x)=24-2x,
y随x的增大而减小.
故选:A.
11.-3
解:∵点P(a,b)在函数y=3x+2的图象上,
∴b=3a+2,
则3a﹣b=﹣2.
∴6a﹣2b+1=2(3a﹣b)+1=﹣4+1=﹣3,
故答案为﹣3.
12.y=-x-2(答案不唯一)
解:∵当时,y随x的增大而减小,可设解析式为y=-x+b,把代入得,
-1=1+b,
解得,b=-2,
所以,函数解析式为:y=-x-2;
故答案为:y=-x-2(答案不唯一).
13.5-2m
方法一:一次函数的图象经过第一、二、四象限,
∴,
∴
.
故答案为:.
方法二:的图象经过第一、二、四象限,
∴解得,
∴,
故答案为.
14.
解:因为A(x1,y1)、B(x2,y2)是一次函数图象上的不同的两个点,
当x1>x2时,y1<y2,
可得:,
解得:a<1.
故答案为:.
15.(0,)
解:过A和B分别作AF⊥OC于F,BE⊥OC于E,
∵∠ACB=90°,
∴∠ACF+∠CAF=90°∠ACF+∠BCE=90°,
∴∠CAF=∠BCE,
在△AFC和△CEB中,
,
∴△AFC≌△CEB(AAS),
∴FC=BE,AF=CE,
∵点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),
∴OC=2,AF=CE=3,OF=6,
∴CF=OF﹣OC=4,OE=CE﹣OC=2﹣1=1,
∴BE=4,
∴则B点的坐标是(1,4),
设直线BC的解析式为:y=kx+b,
则
,
∴
,
∴直线BC的解析式为:y=
x+
,
当x=0时,y=,
∴D(0,).
故答案为:(0,).
16.
解:直线,当时,,当时,,
,
,即为
,,
,
,
即为
同理得:,,
,,
,
∴,
故答案为:.
17.(1)y=-3x-2;(2)(,0),(0,-2)
解:(1)∵一次函数y=kx+b的图象经过(-1,1),(1,-5)两点,
∴,
解得,
∴一次函数的表达式为y=-3x-2;
(2)令y=0,得x=,
∴A(,0),即与x轴交点为(,0),
令x=0,得y=-2,
∴B(0,-2),即与y轴交点为(0,-2).
18.
解:(1)∵与的值互为相反数,
∴+=0,
∴,
解得,,
故,;
(2)由(1)可知,一次函数的图象经过点与点,
代入解析式得,,
解得,,
一次函数解析式为.
19.
(1)依题意得:
解得:,
经检验是原分式方程的解.
(2)设购进甲种绿色袋装食品x袋,表示出乙种绿色袋装食品袋,根据题意得,
,
解得:,
∵x是正整数,,
∴共有7种方案.
(3)设总利润为W,则
①当时,,W随x的增大而增大,
所以,当时,W有最大值,
即此时应购进甲种绿色袋装食品246袋,乙种绿色袋装食品554袋;
②当时,,(2)中所有方案获利都一样;
③当时,,W随x的增大而减小,
所以,当时,W有最大值,
即此时应购进甲种绿色袋装食品240袋,乙种绿色袋装食品560袋.
20.
(1)联立,解得:,
∴;
(2)如图所示,将B沿着x轴对称至B1,
由直线AB的解析式可得:,则,
此时,连接B1E,与x轴交点即为所求F点,
设直线B1E的解析式为:,
将,代入得:
,解得:,
∴直线B1E的解析式为:,
令,解得:,
即:F的坐标为,
∴;
(3)由两直线解析式可得,,
,
①当P点在x轴下方时,,
即:,
则,
解得:或(舍去),
将代入,解得:,
∴;
②当P点在x轴上方时,,
即:,
则,
解得:或(舍去),
将代入,解得:,
∴;
综上,所有满足条件的P的坐标为,.
21.
解:(1)①设的表达式为,
则,得,
∴;
②∵,,
∴点的横坐标为2,点的横坐标为-2,
∴点.
(2)存在.
①当时,点的横坐标为4,
∴,
∴,
∴,
∴直线表达式,
∴,.
②当时,,
∴,
∴点的横坐标为,点和的纵坐标均为,
即.
∴直线表达式,
∴,.
22.
解:(1)如图,连接CQ,过Q作QD⊥PC于点D,
由旋转的性质可得PC=PQ,且∠CPQ=60°,
∴△PCQ为等边三角形,
∵P(1,2)
∴OC=1,PC=2,
∴,
∴,
∵P(a,b),
∴OC=a,PC=b,
∴,
∴;
设M(x,y),则N点坐标为,
∵,
∴,解得,
∴;
故答案为:;;;
(2)①由(1)得
点B的坐标为(,),
设直线OB的解析式为:y=kx,
把B(,)代入y=kx得,=k,
∴
,
∴直线OB的解析式为;
②设直线AB的解析式为:y=mx+n,
把A(2,),B(,)代入y=mx+n得,
,解得
,
∴直线AB的解析式为
,
令x=0,则y=,
∴点D的坐标为(0,).
试卷第1页,总3页
一、单选题
1.若函数是正比例函数,则的取值分别为(
)
A.
B.
C.
D.
2.下列函数①
y=x-6;②
y=;③
y=;④
y=7x中,y是x的一次函数的是
(
)
A.①②③
B.①③④
C.①②③④
D.②③④
3.已知直线与的交点的坐标为,则方程组的解是(
)
A.
B.
C.
D.
4.如图,直线经过点和点,直线过点A,则不等式的解集为(
)
A.
B.
C.
D.
5.若直线y=kx+b经过第一、二、四象限,则函数y=bx-k的大致图像是(
)
A.
B.
C.
D.
6.已知点在函数的图像上,则(
)
A.
B.
C.
D.
与的大小关系不能确定
7.下列关于一次函数的说法,错误的是(
)
A.函数图象与y轴的交点
B.当x值增大时,y随着x的增大而减小
C.当时,
D.图象经过第一、二、三象限
8.如图,一次函数与正比例函数(m,n为常数,且)的图象是( )
A.
B.
C.
D.
9.一次函数y=kx+b(k不为零)的图象与y轴的交点为(0,-3),且与坐标轴围成的三角形的面积为6,则图像与x轴的交点坐标是
(
)
A.(2,0)
B.(4,0)
C.(-4,0)
D.(4,0)或(-4,0)
10.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是(
)
A.
B.
C.
D.
二、填空题
11.点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于_____.
12.请写出一个符合以下两个条件的函数解析式:___________
①过点;②当时,y随x的增大而减小
13.已知一次函数的图象经过第一、二、四象限,则化简__________.
14.若,是一次函数图像上的不同的两个点,当时,,则a的取值范围是_________.
15.如图,在中,,BC与y轴交于D点,点C的坐标为,点A的坐标为,则D点的坐标是__________.
16.将正方形,,按如图所示方式放置,点,,,和点,,,分别在直线和x轴上,则点的坐标是_________.
三、解答题
17.已知一次函数y=kx+b的图象经过点(﹣1,1)和点(1,﹣5)
(1)求一次函数的表达式;
(2)求此函数与x轴,y轴的交点坐标.
18.已知a,b为实数,且与的值互为相反数,
(1)求a、b的值;
(2)若一次函数的图象经过点与点,求这个一次函数的关系式.
19.为了满足学生的物质需求,某中学超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
甲
乙
进价(元/袋)
m
售价(元/袋)
20
13
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求m的值.
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5230元,求该超市进货甲种绿色袋装食品的数量范围.
(3)在(2)的条件下,该超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
20.如图,直线与直线交于点.
(1)求点坐标;
(2)在轴上找一点使得最小,求的长;
(3)若为直线上一点,当面积为6时,求的坐标.
21.如图,在平面直角坐标系中,为坐标原点,点的坐标为,点的坐标为,点是直线上位于第二象限内的一个动点,过点作轴于点,记点关于轴的对称点为.设点的横坐标为.
(1)当时,
①求直线的表达式;
②若,求点的坐标;
(2)是否同时存在,,使得是等腰直角三角形?若存在,求出所有满足条件的,的值;若不存在,请说明理由.
22.操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.
(1)点P(1,2)经过T变换后得到的点Q的坐标为
;点P(a,b)经过T变换后得到的点Q的坐标为
;若点M经过T变换后得到点N(6,),则点M的坐标为
.
(2)点A(2,)是函数y=kx图象上的一点,经过T变换后得到点B.
①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求点D的坐标.
参考答案
1.A
解:∵函数是正比例函数,
∴,
解得:,
2.B
解:函数①y=x-6;③y=
;④y=7x,y是x的一次函数,
故选B.
3.A
将交点(1,a)代入两直线:
得:a=2,a=-1+b,
因此有a=2,b=a+1=3,
即交点为(1,2),
而交点就是两直线组成的方程组的解,
即方程组的解为.
故答案为:A.
4.B
由题意可得:直线y=kx+b与直线y=2x相交于点A,
∴不等式的解集为相当于直线y=2x在直线y=kx+b的下方所对应的x的取值范围和直线y=kx+b在x轴下方所对应的x的取值范围,
观察图象可知,当x<?1时,直线y=2x在直线y=kx+b的下方,当x>?2时,直线y=kx+b在x轴下方,
∴不等式的解集为:-2<
x<?1,
故选:B.
5.B
解:∵一次函数y=kx+b的图象经过第一、二、四象限,
∴k<0,b>0,
∴b>0,-k>0,
∴一次函数y=bx-k图象第一、二、三象限,
6.B
解:∵k=﹣9<0,
∴y随x的增大而减小,
∵﹣1<2,
∴y1>y2?,
7.D
A选项:,当时,则一次函数与y轴交于,A正确,故不符合题意;
B选项:,斜率,则,y随x增大而减小,B正确,故不符合题意;
C选项:,即,解得,C正确,故不符合题意;
D选项:,与y轴交于,与x轴交于,则图象过一、二、四象限,D错误,故符合题意.
8.A
A、由不过原点的一次函数图象得m<0,n>0,所以mn<0,则正比例函数图象过第二、四象限,所以A选项符合题意;
B、由不过原点的一次函数图象得m<0,n>0,所以mn<0,则正比例函数图象过第二、四象限,所以B选项不符合题意.
C、由不过原点的一次函数图象得m>0,n>0,所以mn>0,则正比例函数图象过第一、三象限,所以C选项不符合题意;
D、由不过原点的一次函数图象得m>0,n<0,所以mn<0,则正比例函数图象过第二、四象限,所以D选项不符合题意;
故选择:A.
9.D
解:把(0,-3)代入y=kx+b得b=-3,
把y=0代入y=kx-3得kx-3=0,解得:x=,
∵一次函数y=kx+b的图象与两坐标轴围成的三角形面积为6,
∴,解得:=±4
∴该函数图像与x轴的交点为(4,0)或(-4,0).
10.A
解:当点P由点D向点C运动,即0<x≤4时,y=AD?x=×4x=2x,y随x的增大而增大;
当点P在BC上运动,即4<x≤8时,y=×4×4=8,y是一个定值;
当点P在BA上运动,即8<x<12时,y=AD?(12-x)=24-2x,
y随x的增大而减小.
故选:A.
11.-3
解:∵点P(a,b)在函数y=3x+2的图象上,
∴b=3a+2,
则3a﹣b=﹣2.
∴6a﹣2b+1=2(3a﹣b)+1=﹣4+1=﹣3,
故答案为﹣3.
12.y=-x-2(答案不唯一)
解:∵当时,y随x的增大而减小,可设解析式为y=-x+b,把代入得,
-1=1+b,
解得,b=-2,
所以,函数解析式为:y=-x-2;
故答案为:y=-x-2(答案不唯一).
13.5-2m
方法一:一次函数的图象经过第一、二、四象限,
∴,
∴
.
故答案为:.
方法二:的图象经过第一、二、四象限,
∴解得,
∴,
故答案为.
14.
解:因为A(x1,y1)、B(x2,y2)是一次函数图象上的不同的两个点,
当x1>x2时,y1<y2,
可得:,
解得:a<1.
故答案为:.
15.(0,)
解:过A和B分别作AF⊥OC于F,BE⊥OC于E,
∵∠ACB=90°,
∴∠ACF+∠CAF=90°∠ACF+∠BCE=90°,
∴∠CAF=∠BCE,
在△AFC和△CEB中,
,
∴△AFC≌△CEB(AAS),
∴FC=BE,AF=CE,
∵点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),
∴OC=2,AF=CE=3,OF=6,
∴CF=OF﹣OC=4,OE=CE﹣OC=2﹣1=1,
∴BE=4,
∴则B点的坐标是(1,4),
设直线BC的解析式为:y=kx+b,
则
,
∴
,
∴直线BC的解析式为:y=
x+
,
当x=0时,y=,
∴D(0,).
故答案为:(0,).
16.
解:直线,当时,,当时,,
,
,即为
,,
,
,
即为
同理得:,,
,,
,
∴,
故答案为:.
17.(1)y=-3x-2;(2)(,0),(0,-2)
解:(1)∵一次函数y=kx+b的图象经过(-1,1),(1,-5)两点,
∴,
解得,
∴一次函数的表达式为y=-3x-2;
(2)令y=0,得x=,
∴A(,0),即与x轴交点为(,0),
令x=0,得y=-2,
∴B(0,-2),即与y轴交点为(0,-2).
18.
解:(1)∵与的值互为相反数,
∴+=0,
∴,
解得,,
故,;
(2)由(1)可知,一次函数的图象经过点与点,
代入解析式得,,
解得,,
一次函数解析式为.
19.
(1)依题意得:
解得:,
经检验是原分式方程的解.
(2)设购进甲种绿色袋装食品x袋,表示出乙种绿色袋装食品袋,根据题意得,
,
解得:,
∵x是正整数,,
∴共有7种方案.
(3)设总利润为W,则
①当时,,W随x的增大而增大,
所以,当时,W有最大值,
即此时应购进甲种绿色袋装食品246袋,乙种绿色袋装食品554袋;
②当时,,(2)中所有方案获利都一样;
③当时,,W随x的增大而减小,
所以,当时,W有最大值,
即此时应购进甲种绿色袋装食品240袋,乙种绿色袋装食品560袋.
20.
(1)联立,解得:,
∴;
(2)如图所示,将B沿着x轴对称至B1,
由直线AB的解析式可得:,则,
此时,连接B1E,与x轴交点即为所求F点,
设直线B1E的解析式为:,
将,代入得:
,解得:,
∴直线B1E的解析式为:,
令,解得:,
即:F的坐标为,
∴;
(3)由两直线解析式可得,,
,
①当P点在x轴下方时,,
即:,
则,
解得:或(舍去),
将代入,解得:,
∴;
②当P点在x轴上方时,,
即:,
则,
解得:或(舍去),
将代入,解得:,
∴;
综上,所有满足条件的P的坐标为,.
21.
解:(1)①设的表达式为,
则,得,
∴;
②∵,,
∴点的横坐标为2,点的横坐标为-2,
∴点.
(2)存在.
①当时,点的横坐标为4,
∴,
∴,
∴,
∴直线表达式,
∴,.
②当时,,
∴,
∴点的横坐标为,点和的纵坐标均为,
即.
∴直线表达式,
∴,.
22.
解:(1)如图,连接CQ,过Q作QD⊥PC于点D,
由旋转的性质可得PC=PQ,且∠CPQ=60°,
∴△PCQ为等边三角形,
∵P(1,2)
∴OC=1,PC=2,
∴,
∴,
∵P(a,b),
∴OC=a,PC=b,
∴,
∴;
设M(x,y),则N点坐标为,
∵,
∴,解得,
∴;
故答案为:;;;
(2)①由(1)得
点B的坐标为(,),
设直线OB的解析式为:y=kx,
把B(,)代入y=kx得,=k,
∴
,
∴直线OB的解析式为;
②设直线AB的解析式为:y=mx+n,
把A(2,),B(,)代入y=mx+n得,
,解得
,
∴直线AB的解析式为
,
令x=0,则y=,
∴点D的坐标为(0,).
试卷第1页,总3页
