2020-2021学年人教版八年级下册 18.1.2 第三课时 三角形的中位线数学课件(39张ppt)
文档属性
| 名称 | 2020-2021学年人教版八年级下册 18.1.2 第三课时 三角形的中位线数学课件(39张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 00:00:00 | ||
图片预览






文档简介
(共39张PPT)
数
学
人教˙八年级(下册)
18
平行四边形
18.1.2
平行四边形的判定
第三课时
三角形的中位线
课时目标
1.理解三角形中位线的概念,掌握三角形的中位线定理。
2.能利用三角形的中位线定理解决有关证明和计算问题。
情景导入
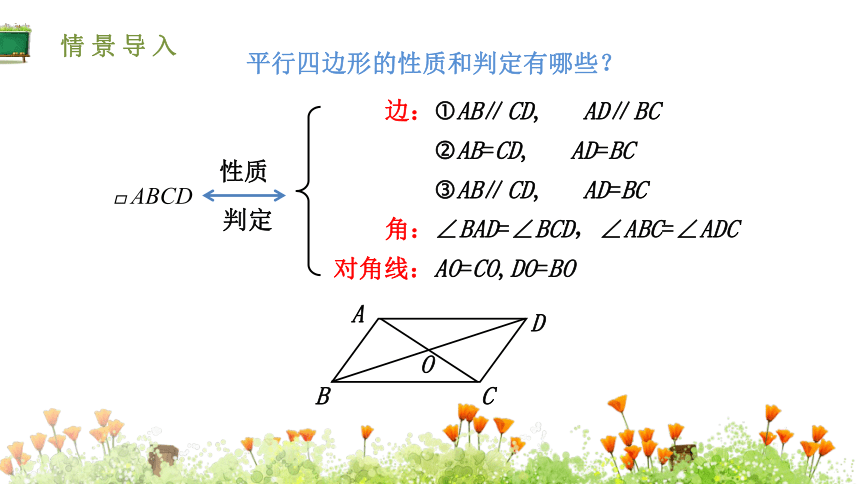
平行四边形的性质和判定有哪些?
边:
角:
对角线:
B
O
D
A
C
?AB∥CD,
AD∥BC
?AB=CD,
AD=BC
?AB∥CD,
AD=BC
∠BAD=∠BCD,∠ABC=∠ADC
AO=CO,DO=BO
判定
性质
探究新知
三角形的中位线定理
定义:连接三角形两边中点的线段叫做三角形的中位线.
A
B
C
D
E
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.则线段DE就称为△ABC的中位线.
探究新知
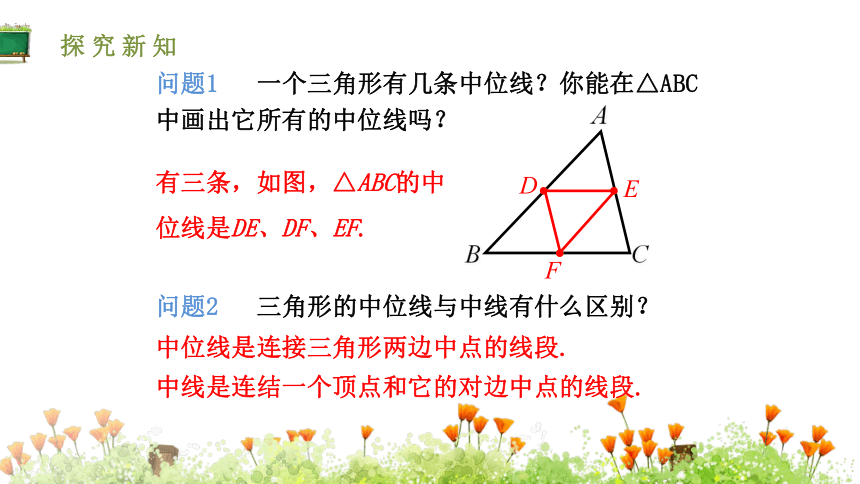
问题1
一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
有三条,如图,△ABC的中位线是DE、DF、EF.
问题2
三角形的中位线与中线有什么区别?
中位线是连接三角形两边中点的线段.
中线是连结一个顶点和它的对边中点的线段.
A
B
C
D
E
F
探究新知
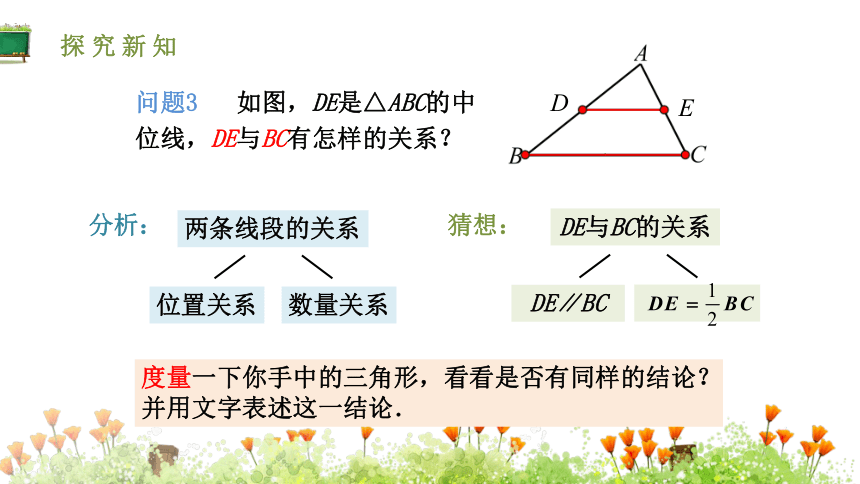
问题3
如图,DE是△ABC的中位线,DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
探究新知
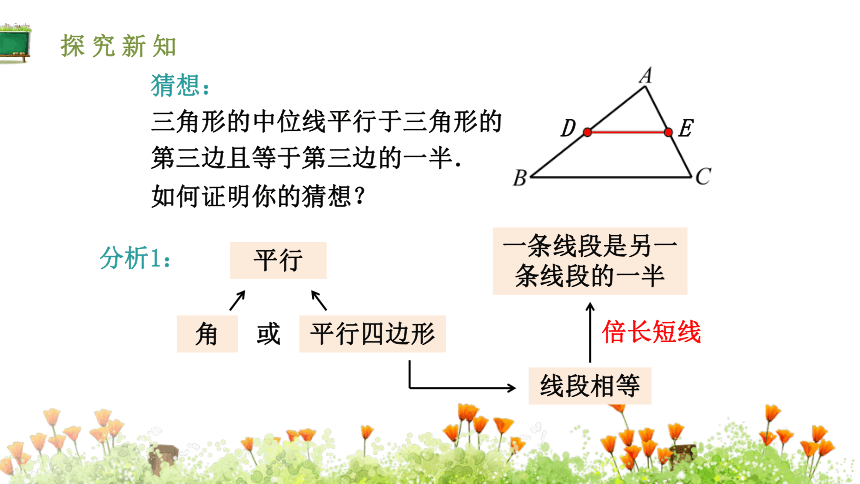
平行
一条线段是另一条线段的一半
倍长短线
线段相等
分析1:
D
E
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
如何证明你的猜想?
角
平行四边形
或
探究新知
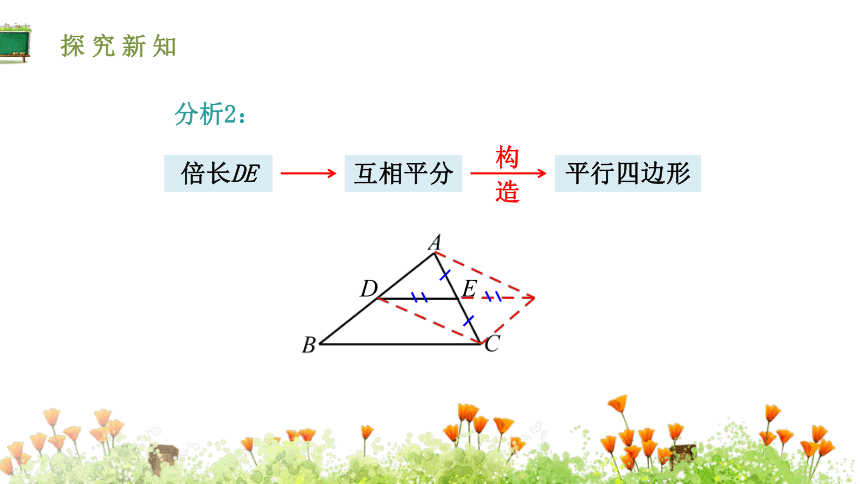
分析2:
D
E
互相平分
构造
平行四边形
倍长DE
探究新知
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC
.
∵AE=EC,DE=EF
,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形,
∴CF
AD
,
∴CF
BD
,
又∵
,
∴DF
BC
.
∴DE∥BC,
.
如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:
探究新知
D
E
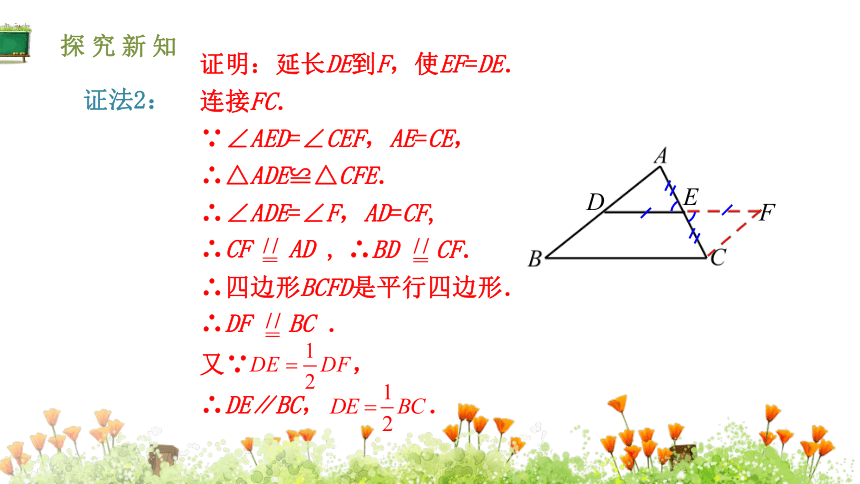
证明:延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F,AD=CF,
连接FC.
∵∠AED=∠CEF,AE=CE,
证法2:
∴BD
CF.
又∵
,
∴DF
BC
.
∴DE∥BC,
.
∴CF
AD
,
探究新知
归纳总结
D
E
符号语言:
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE=
BC.
三角形中位线定理:
三角形的中位线平行于三角形的第三边且等于第三边的一半.
探究新知
重要发现:
①中位线DE、EF、DF把△ABC分成四个全等的三角形;有三组共边的平行四边形,它们是四边形ADFE和BDEF,四边形BFED和CFDE,四边形ADFE和DFCE.
②顶点是中点的三角形,我们称之为中点三角形;中点三角形的周长是原三角形的周长的一半.面积等于原三角形面积的四分之一.
A
B
C
D
E
F
探究新知
例1
如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,
∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3,
∴∠1=∠2,
∴AD=DF=3,
∴AC=2AD=2DF=6.
1
2
3
探究新知
例2
如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
探究新知
解:∵M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=
AB,PN=
DC,PM∥AB,PN∥DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+(180°?∠NPB)=130°,
∴∠PMN=(180°?130°)÷
2
=25°.
探究新知
例3
如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
探究新知
证明:取AC的中点F,连接BF.
∵BD=AB,
∴BF为△ADC的中位线,∴DC=2BF.
∵E为AB的中点,AB=AC,
∴BE=CF,∠ABC=∠ACB.
∵BC=CB,∴△EBC≌△FCB,
∴CE=BF,
∴CD=2CE.
F
恰当地构造三角形中位线是解决线段倍分关系的关键.
巩固练习
1.
如图,△ABC中,D、E分别是AB、AC中点.
(1)
若DE=5,则BC=
.
(2)
若∠B=65°,则∠ADE=
°.
(3)
若DE+BC=12,则BC=
.
10
65
8
巩固练习
2.如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离为______m.
N
M
40
探究新知
三角形的中位线的与平行四边形的综合运用
例4
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
连接对角线
三角形问题
(三角形中位线定理)
四边形问题
分析:
探究新知
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴
EF∥HG,
EF=HG.
∴EF∥AC,
HG∥AC,
∴四边形EFGH是平行四边形.
顺次连结四边形四条边的中点,所得的四边形是平行四边形.
探究新知
【变式题】如图,E、F、G、H分别为四边形ABCD四边之中点.求证:四边形EFGH为平行四边形.
探究新知
证明:如图,连接BD.
∵E、F、G、H分别为四边形ABCD四边之中点,
∴EH是△ABD的中位线,
FG是△BCD的中位线,
∴EH∥BD且EH=
BD,FG∥BD且FG=
BD,
∴EH∥FG且EH=FG,
∴四边形EFGH为平行四边形.
探究新知
证明:∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥
BC,DE=
BC.
∵CF=
BC,
∴DE=FC;
例5
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
BC,连接CD和EF.
(1)求证:DE=CF;
探究新知
(2)求EF的长.
解:∵DE∥FC,DE=FC,
∴四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴EF=DC=
.
巩固练习
1.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
A.8
B.10
C.12
D.16
D
巩固练习
2.如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵?ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE=
CD,
∴OE=
BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
巩固练习
1.如图,在△ABC中,点E、F分别为AB、AC的中点.若EF的长为2,则BC的长为( )
A.1
B.2
C.4
D.8
C
巩固练习
2.如图,在?ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于( )
A.2
B.3
C.4
D.5
C
巩固练习
3.如图,点
D、E、F
分别是
△ABC
的三边AB、BC、AC的中点.
(1)若∠ADF=50°,则∠B=
°;
(2)已知三边AB、BC、AC分别为12、10、8,则△
DEF的周长为
.
50
15
A
B
C
D
F
E
巩固练习
4.在△ABC中,E、F、G、H分别为AC、CD、
BD、
AB的中点,若AD=3,BC=8,则四边形EFGH的周长是
.
A
B
D
C
E
F
G
H
11
巩固练习
5.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于
点F,E为BC的中点,求DE的长.
解:∵AD平分∠BAC,BD⊥AD,
∴AB=AF=6,BD=DF,
∴CF=AC-AF=4,
∵BD=DF,E为BC的中点,
∴DE=
CF=2.
巩固练习
6.如图,E为?ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.
巩固练习
解:AB∥OF,AB=2OF.
证明如下:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OA=OC,
∴∠BAF=∠CEF,∠ABF=∠ECF.
∵CE=DC,
∴AB=CE,
∴△ABF≌△ECF(ASA),
∴BF=CF.∵OA=OC,
∴OF是△ABC的中位线,
∴AB∥OF,AB=2OF.
巩固练习
7.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.
巩固练习
解:取BC边的中点G,连接EG、FG.
∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线,
又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG,
∴
∴EG∥AC,
FG∥BD,
G
课堂小结
三角形的中位线
三角形中位线平行于第三边,并且等于它的一半
三角形的中位线定理
三角形的中位线定理的应用
谢谢观看
数
学
人教˙八年级(下册)
18
平行四边形
18.1.2
平行四边形的判定
第三课时
三角形的中位线
课时目标
1.理解三角形中位线的概念,掌握三角形的中位线定理。
2.能利用三角形的中位线定理解决有关证明和计算问题。
情景导入
平行四边形的性质和判定有哪些?
边:
角:
对角线:
B
O
D
A
C
?AB∥CD,
AD∥BC
?AB=CD,
AD=BC
?AB∥CD,
AD=BC
∠BAD=∠BCD,∠ABC=∠ADC
AO=CO,DO=BO
判定
性质
探究新知
三角形的中位线定理
定义:连接三角形两边中点的线段叫做三角形的中位线.
A
B
C
D
E
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.则线段DE就称为△ABC的中位线.
探究新知
问题1
一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
有三条,如图,△ABC的中位线是DE、DF、EF.
问题2
三角形的中位线与中线有什么区别?
中位线是连接三角形两边中点的线段.
中线是连结一个顶点和它的对边中点的线段.
A
B
C
D
E
F
探究新知
问题3
如图,DE是△ABC的中位线,DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
探究新知
平行
一条线段是另一条线段的一半
倍长短线
线段相等
分析1:
D
E
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
如何证明你的猜想?
角
平行四边形
或
探究新知
分析2:
D
E
互相平分
构造
平行四边形
倍长DE
探究新知
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC
.
∵AE=EC,DE=EF
,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形,
∴CF
AD
,
∴CF
BD
,
又∵
,
∴DF
BC
.
∴DE∥BC,
.
如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:
探究新知
D
E
证明:延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F,AD=CF,
连接FC.
∵∠AED=∠CEF,AE=CE,
证法2:
∴BD
CF.
又∵
,
∴DF
BC
.
∴DE∥BC,
.
∴CF
AD
,
探究新知
归纳总结
D
E
符号语言:
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE=
BC.
三角形中位线定理:
三角形的中位线平行于三角形的第三边且等于第三边的一半.
探究新知
重要发现:
①中位线DE、EF、DF把△ABC分成四个全等的三角形;有三组共边的平行四边形,它们是四边形ADFE和BDEF,四边形BFED和CFDE,四边形ADFE和DFCE.
②顶点是中点的三角形,我们称之为中点三角形;中点三角形的周长是原三角形的周长的一半.面积等于原三角形面积的四分之一.
A
B
C
D
E
F
探究新知
例1
如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,
∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3,
∴∠1=∠2,
∴AD=DF=3,
∴AC=2AD=2DF=6.
1
2
3
探究新知
例2
如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
探究新知
解:∵M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=
AB,PN=
DC,PM∥AB,PN∥DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,
∴∠MPN=∠MPD+(180°?∠NPB)=130°,
∴∠PMN=(180°?130°)÷
2
=25°.
探究新知
例3
如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
探究新知
证明:取AC的中点F,连接BF.
∵BD=AB,
∴BF为△ADC的中位线,∴DC=2BF.
∵E为AB的中点,AB=AC,
∴BE=CF,∠ABC=∠ACB.
∵BC=CB,∴△EBC≌△FCB,
∴CE=BF,
∴CD=2CE.
F
恰当地构造三角形中位线是解决线段倍分关系的关键.
巩固练习
1.
如图,△ABC中,D、E分别是AB、AC中点.
(1)
若DE=5,则BC=
.
(2)
若∠B=65°,则∠ADE=
°.
(3)
若DE+BC=12,则BC=
.
10
65
8
巩固练习
2.如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离为______m.
N
M
40
探究新知
三角形的中位线的与平行四边形的综合运用
例4
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
连接对角线
三角形问题
(三角形中位线定理)
四边形问题
分析:
探究新知
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴
EF∥HG,
EF=HG.
∴EF∥AC,
HG∥AC,
∴四边形EFGH是平行四边形.
顺次连结四边形四条边的中点,所得的四边形是平行四边形.
探究新知
【变式题】如图,E、F、G、H分别为四边形ABCD四边之中点.求证:四边形EFGH为平行四边形.
探究新知
证明:如图,连接BD.
∵E、F、G、H分别为四边形ABCD四边之中点,
∴EH是△ABD的中位线,
FG是△BCD的中位线,
∴EH∥BD且EH=
BD,FG∥BD且FG=
BD,
∴EH∥FG且EH=FG,
∴四边形EFGH为平行四边形.
探究新知
证明:∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥
BC,DE=
BC.
∵CF=
BC,
∴DE=FC;
例5
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
BC,连接CD和EF.
(1)求证:DE=CF;
探究新知
(2)求EF的长.
解:∵DE∥FC,DE=FC,
∴四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴EF=DC=
.
巩固练习
1.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
A.8
B.10
C.12
D.16
D
巩固练习
2.如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵?ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE=
CD,
∴OE=
BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
巩固练习
1.如图,在△ABC中,点E、F分别为AB、AC的中点.若EF的长为2,则BC的长为( )
A.1
B.2
C.4
D.8
C
巩固练习
2.如图,在?ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于( )
A.2
B.3
C.4
D.5
C
巩固练习
3.如图,点
D、E、F
分别是
△ABC
的三边AB、BC、AC的中点.
(1)若∠ADF=50°,则∠B=
°;
(2)已知三边AB、BC、AC分别为12、10、8,则△
DEF的周长为
.
50
15
A
B
C
D
F
E
巩固练习
4.在△ABC中,E、F、G、H分别为AC、CD、
BD、
AB的中点,若AD=3,BC=8,则四边形EFGH的周长是
.
A
B
D
C
E
F
G
H
11
巩固练习
5.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于
点F,E为BC的中点,求DE的长.
解:∵AD平分∠BAC,BD⊥AD,
∴AB=AF=6,BD=DF,
∴CF=AC-AF=4,
∵BD=DF,E为BC的中点,
∴DE=
CF=2.
巩固练习
6.如图,E为?ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.
巩固练习
解:AB∥OF,AB=2OF.
证明如下:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OA=OC,
∴∠BAF=∠CEF,∠ABF=∠ECF.
∵CE=DC,
∴AB=CE,
∴△ABF≌△ECF(ASA),
∴BF=CF.∵OA=OC,
∴OF是△ABC的中位线,
∴AB∥OF,AB=2OF.
巩固练习
7.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.
巩固练习
解:取BC边的中点G,连接EG、FG.
∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线,
又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG,
∴
∴EG∥AC,
FG∥BD,
G
课堂小结
三角形的中位线
三角形中位线平行于第三边,并且等于它的一半
三角形的中位线定理
三角形的中位线定理的应用
谢谢观看
