人教版八年级上册数学课件:12.2全等三角形的判定(3)— ASA AAS(共17张PPT)
文档属性
| 名称 | 人教版八年级上册数学课件:12.2全等三角形的判定(3)— ASA AAS(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 683.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
第十二章
全等三角形
三角形全等的判定(3)
—
ASA
AAS
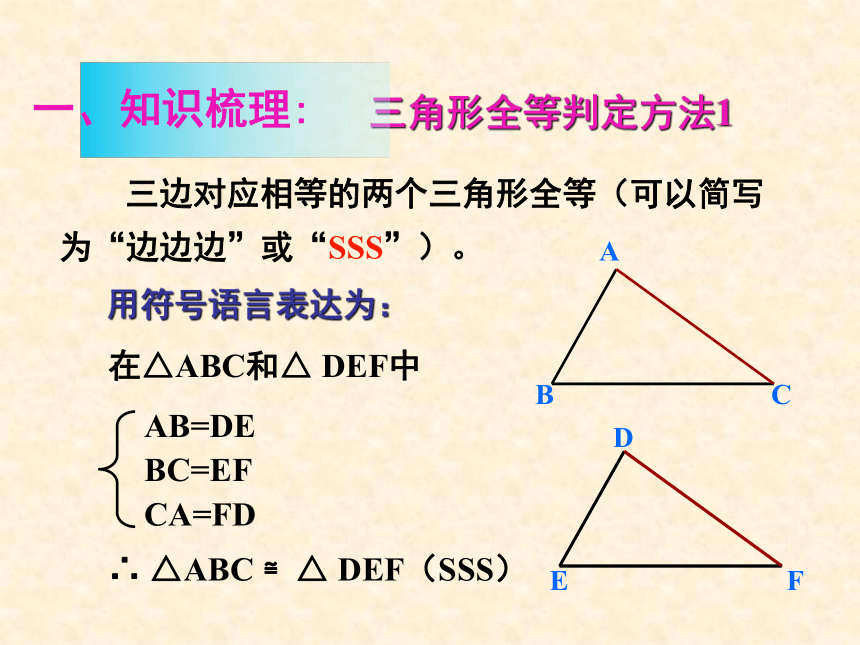
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
一、知识梳理:
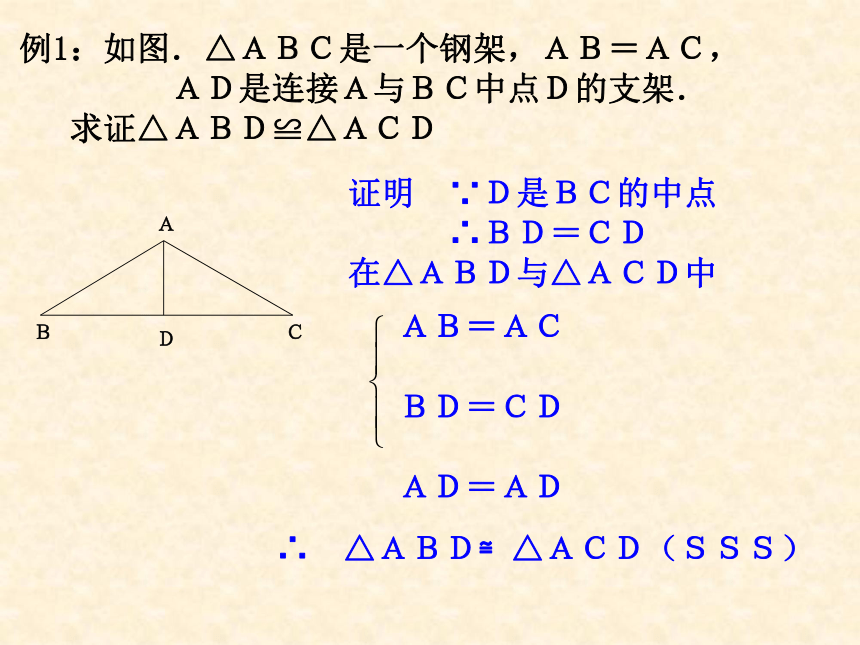
例1:如图.△ABC是一个钢架,AB=AC,
AD是连接A与BC中点D的支架.
求证△ABD≌△ACD
A
D
C
B
证明 ∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC
BD=CD
AD=AD
∴ △ABD≌△ACD(SSS)
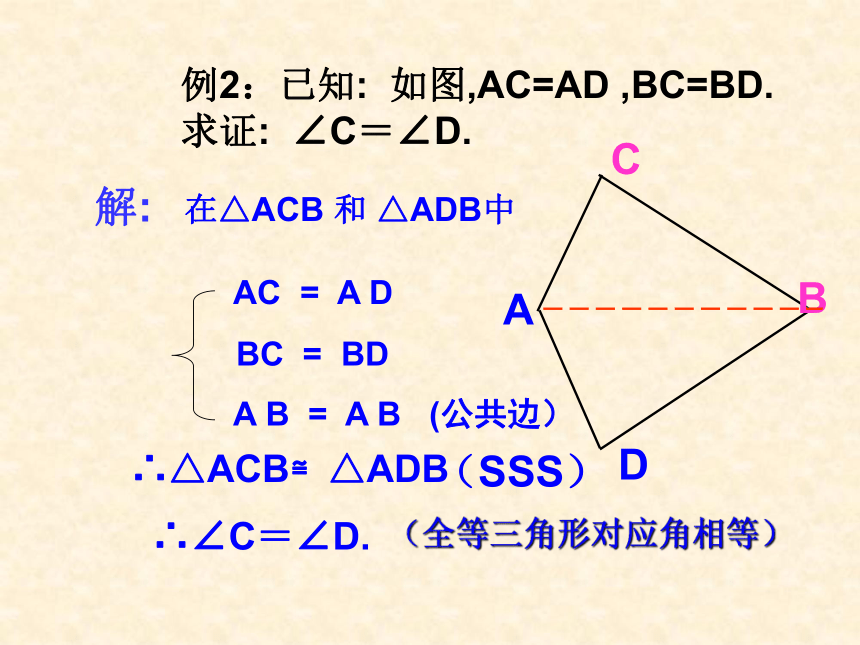
例2:已知:
如图,AC=AD
,BC=BD.
求证:
∠C=∠D.
A
B
C
D
解:
在△ACB
和
△ADB中
AC
=
A
D
BC
=
BD
A
B
=
A
B
(公共边)
∴△ACB≌△ADB
(SSS)
∴∠C=∠D.
(全等三角形对应角相等)
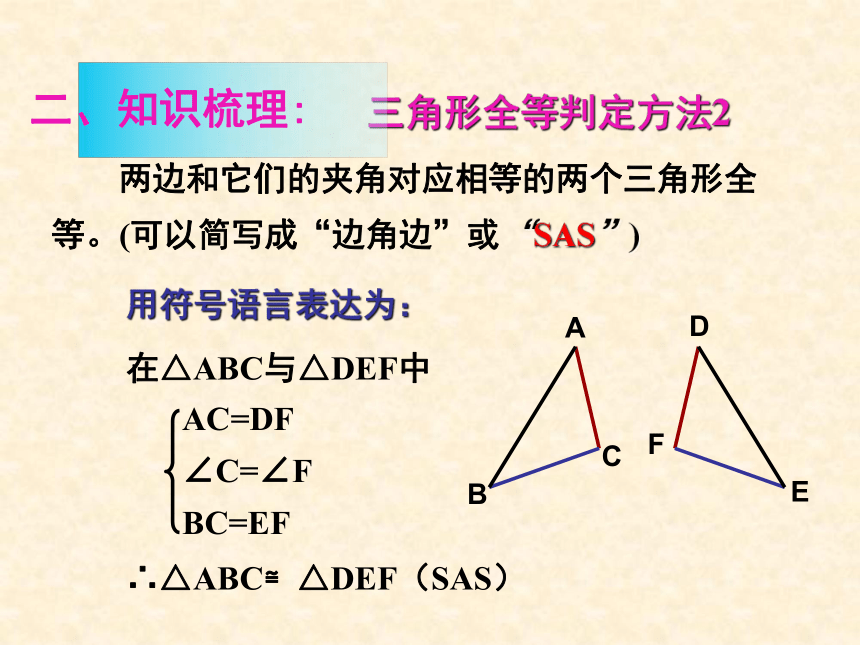
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
二、知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
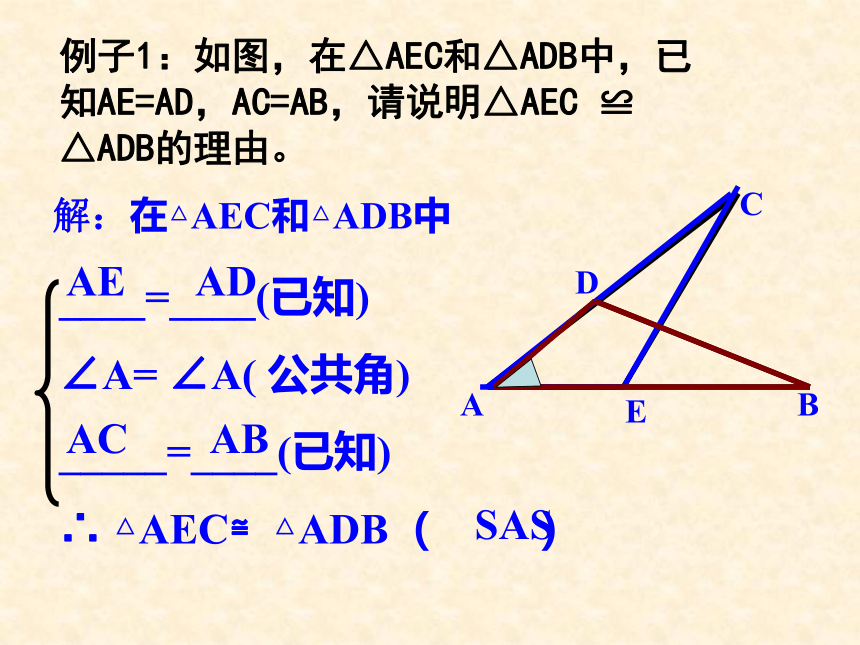
例子1:如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC
≌
△ADB的理由。
____=____(已知)
∠A=
∠A(
公共角)
_____=____(已知)
∴
△AEC≌△ADB(
)
A
E
B
D
C
AE
AD
AC
AB
SAS
解:在△AEC和△ADB中
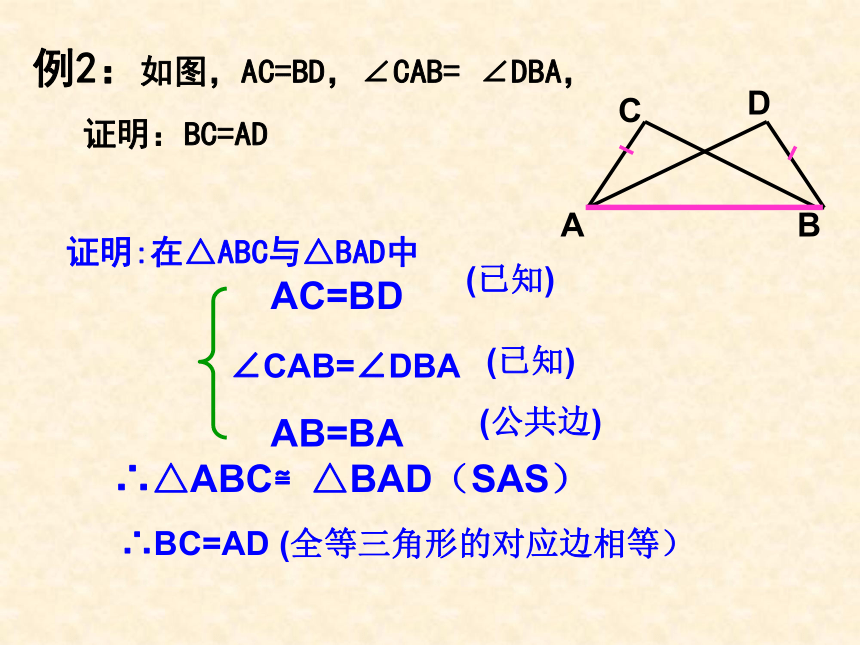
例2:如图,AC=BD,∠CAB=
∠DBA,
证明:BC=AD
A
B
C
D
证明:在△ABC与△BAD中
AC=BD
∠CAB=∠DBA
AB=BA
∴△ABC≌△BAD(SAS)
(已知)
(已知)
(公共边)
∴BC=AD
(全等三角形的对应边相等)
∠A=∠D
(已知
)
AB=DE(已知
)
∠B=∠E(已知
)
在△ABC和△DEF中
∴
△ABC≌△DEF(ASA)
有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
用符号语言表达为:
F
E
D
C
B
A
三角形全等判定方法3
三、知识梳理:
例1:
已知如图,O是AB的中点,∠A=∠B,
A
B
C
D
O
1
2
∵
O是AB的中点(已知)
∴
OA=OB(中点定义)
求证:△AOC≌△BOD
在△AOC和△BOD中
证明:
∠A=
∠B
OA=OB
∠1=
∠2
(已知)
(已证)
(对顶角相等)
∴
△AOC≌△BO(ASA)
例2:
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,
∠B=
∠C
求证:
∴△ADC≌△AEB
AD=AE.
B
A
E
C
D
O
证明:在△ADC和△AEB中
∠A=
∠A
AC=AB
∠C=
∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
(全等三角形的对应边相等)
证明:在△ABC与△A
B
C
中
∠A=∠A
∴△ABC≌△A’B’C’(AAS)
A
C
B
A
′
C
B
′
′
′
′
′
′
∠B=∠B
′
′
′
BC=B
C
有两角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。
三角形全等判定方法4
四、知识梳理:
例3:已知如图,
∠1=∠2,
∠C=∠D
求证:AD=AC.
1
A
B
D
C
2
证明:在△ABD和△ABC中
∠1=∠2
∠D=∠C
AB=AB
∴△ABD≌△ABC(AAS)
∴AD=AC
斜边、直角边公理
(HL)推理格式
A
B
C
A
′
B′
C
′
∴在Rt△ABC和Rt△A?B?C?中
AB=A?B?
BC=B?C?
∴Rt△ABC≌
∵∠C=∠C′=90°
Rt△A?B?C?
(HL)
三角形全等判定方法5
五、知识梳理:
已知:如图,在△ABC和△ABD中,AC⊥BC,
BD⊥AD,垂足分别为C,D,AC=BD
(1)求证:
△ABC≌△BAD.
(2)求证:BC=AD
A
B
D
C
(1)解:
∵
AC⊥BC,
BD⊥AD
∴
∠C=∠D=90°
在Rt△ABC和
Rt△BAD中
,有
AB=AB,
AC=AD.
∴
Rt△ACB≌Rt△ADB
(HL).
(2)∵
Rt△ACB≌Rt△ADB
(HL).
∴
BC=AD
例2.
如图,AC=AD,∠C,∠D是直角,
将上述条件标注在图中,求证BC=BD
C
D
A
B
解:在Rt△ACB和
Rt△ADB中,有
AB=AB,
AC=AD.
∴
Rt△ACB≌Rt△ADB
(HL).
∴BC=BD
(全等三角形对应边相等).
小结
直角三角形全等的识别
一般三角形全等的识别
S.A.S
A.S.A
A.A.S
S.S.S
H.L
灵活运用各种方法证明直角三角形全等
谢谢!
第十二章
全等三角形
三角形全等的判定(3)
—
ASA
AAS
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
一、知识梳理:
例1:如图.△ABC是一个钢架,AB=AC,
AD是连接A与BC中点D的支架.
求证△ABD≌△ACD
A
D
C
B
证明 ∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC
BD=CD
AD=AD
∴ △ABD≌△ACD(SSS)
例2:已知:
如图,AC=AD
,BC=BD.
求证:
∠C=∠D.
A
B
C
D
解:
在△ACB
和
△ADB中
AC
=
A
D
BC
=
BD
A
B
=
A
B
(公共边)
∴△ACB≌△ADB
(SSS)
∴∠C=∠D.
(全等三角形对应角相等)
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
二、知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
例子1:如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC
≌
△ADB的理由。
____=____(已知)
∠A=
∠A(
公共角)
_____=____(已知)
∴
△AEC≌△ADB(
)
A
E
B
D
C
AE
AD
AC
AB
SAS
解:在△AEC和△ADB中
例2:如图,AC=BD,∠CAB=
∠DBA,
证明:BC=AD
A
B
C
D
证明:在△ABC与△BAD中
AC=BD
∠CAB=∠DBA
AB=BA
∴△ABC≌△BAD(SAS)
(已知)
(已知)
(公共边)
∴BC=AD
(全等三角形的对应边相等)
∠A=∠D
(已知
)
AB=DE(已知
)
∠B=∠E(已知
)
在△ABC和△DEF中
∴
△ABC≌△DEF(ASA)
有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
用符号语言表达为:
F
E
D
C
B
A
三角形全等判定方法3
三、知识梳理:
例1:
已知如图,O是AB的中点,∠A=∠B,
A
B
C
D
O
1
2
∵
O是AB的中点(已知)
∴
OA=OB(中点定义)
求证:△AOC≌△BOD
在△AOC和△BOD中
证明:
∠A=
∠B
OA=OB
∠1=
∠2
(已知)
(已证)
(对顶角相等)
∴
△AOC≌△BO(ASA)
例2:
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,
∠B=
∠C
求证:
∴△ADC≌△AEB
AD=AE.
B
A
E
C
D
O
证明:在△ADC和△AEB中
∠A=
∠A
AC=AB
∠C=
∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
(全等三角形的对应边相等)
证明:在△ABC与△A
B
C
中
∠A=∠A
∴△ABC≌△A’B’C’(AAS)
A
C
B
A
′
C
B
′
′
′
′
′
′
∠B=∠B
′
′
′
BC=B
C
有两角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。
三角形全等判定方法4
四、知识梳理:
例3:已知如图,
∠1=∠2,
∠C=∠D
求证:AD=AC.
1
A
B
D
C
2
证明:在△ABD和△ABC中
∠1=∠2
∠D=∠C
AB=AB
∴△ABD≌△ABC(AAS)
∴AD=AC
斜边、直角边公理
(HL)推理格式
A
B
C
A
′
B′
C
′
∴在Rt△ABC和Rt△A?B?C?中
AB=A?B?
BC=B?C?
∴Rt△ABC≌
∵∠C=∠C′=90°
Rt△A?B?C?
(HL)
三角形全等判定方法5
五、知识梳理:
已知:如图,在△ABC和△ABD中,AC⊥BC,
BD⊥AD,垂足分别为C,D,AC=BD
(1)求证:
△ABC≌△BAD.
(2)求证:BC=AD
A
B
D
C
(1)解:
∵
AC⊥BC,
BD⊥AD
∴
∠C=∠D=90°
在Rt△ABC和
Rt△BAD中
,有
AB=AB,
AC=AD.
∴
Rt△ACB≌Rt△ADB
(HL).
(2)∵
Rt△ACB≌Rt△ADB
(HL).
∴
BC=AD
例2.
如图,AC=AD,∠C,∠D是直角,
将上述条件标注在图中,求证BC=BD
C
D
A
B
解:在Rt△ACB和
Rt△ADB中,有
AB=AB,
AC=AD.
∴
Rt△ACB≌Rt△ADB
(HL).
∴BC=BD
(全等三角形对应边相等).
小结
直角三角形全等的识别
一般三角形全等的识别
S.A.S
A.S.A
A.A.S
S.S.S
H.L
灵活运用各种方法证明直角三角形全等
谢谢!
