2020-2021学年人教版八年级数学下册18.1平行四边形经典好题优生辅导训练(Word版,附答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册18.1平行四边形经典好题优生辅导训练(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 299.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 00:04:05 | ||
图片预览



文档简介
2020-2021年度人教版八年级数学下册《18.1平行四边形》经典好题优生辅导训练(附答案)
1.如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=5,AB=13,则BD的长是
.
2.?ABCD的对角线AC,BD相交于点O.已知AB=5cm,△AOB的周长和△BOC的周长相差3cm,则AD的长为
.
3.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=6cm,AD=12cm,BC=15CM.点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以2cm/s的速度向点B运动,规定其t=
s时,PQ∥CD且PQ=CD.
4.如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是
.
5.如图,△ABC中,已知M是BC边的中点,AN平分∠BAC,BN⊥AN,若AB=8cm,AC=16cm,则MN=
cm.
6.如图,在?ABCD中,E、F分别是AD、DC的中点,若△CEF的面积为3,则?ABCD的面积为
.
7.平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为
.
8.已知?ABCD中,AB=7,∠ADC与∠BCD的平分线分别交边AB于点F、E,若EF=1,则BC的长为
.
9.如图,在?ABCD中,DB=DC,∠A=67°,CE⊥BD于点E,则∠BCE=
.
10.如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是
.
11.如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=
.
12.在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是O(0,0),A(﹣3,0),B(0,2),则平行四边形第四个顶点C的坐标
.
13.如图,在?ABCD中,点E在AD上,BD平分∠EBC.若?ABCD的周长为10,则△AEB的周长为
.
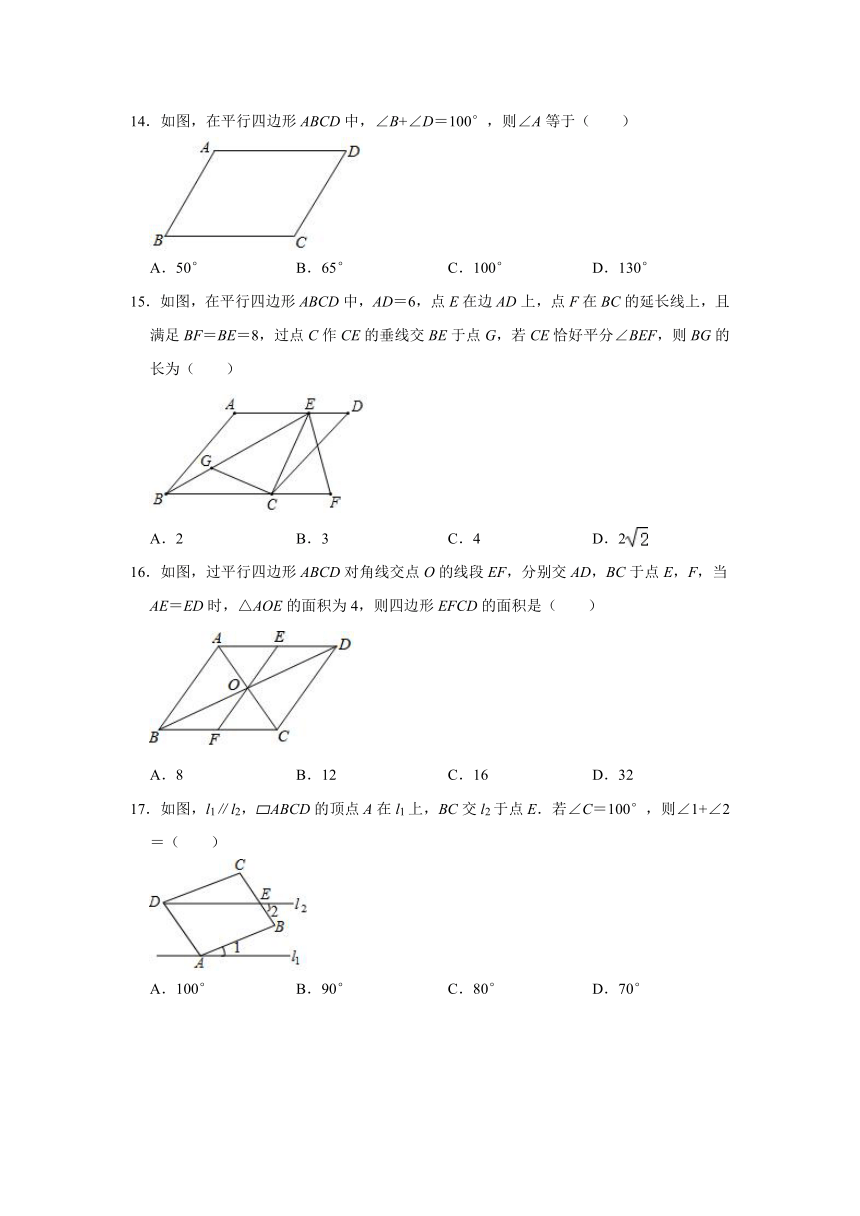
14.如图,在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
A.50°
B.65°
C.100°
D.130°
15.如图,在平行四边形ABCD中,AD=6,点E在边AD上,点F在BC的延长线上,且满足BF=BE=8,过点C作CE的垂线交BE于点G,若CE恰好平分∠BEF,则BG的长为( )
A.2
B.3
C.4
D.2
16.如图,过平行四边形ABCD对角线交点O的线段EF,分别交AD,BC于点E,F,当AE=ED时,△AOE的面积为4,则四边形EFCD的面积是( )
A.8
B.12
C.16
D.32
17.如图,l1∥l2,?ABCD的顶点A在l1上,BC交l2于点E.若∠C=100°,则∠1+∠2=( )
A.100°
B.90°
C.80°
D.70°
18.如图,在平行四边形ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.下列结论,其中正确的有( )个.
①DE=DF;②AG=GF;③AF=DF;④BG=GC;⑤BF=EF.
A.1
B.2
C.3
D.4
19.如图,平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,CE交GH于点O,已知S?ABCD=a,S?EFGH=b(a<b),则S阴影为( )
A.b﹣a
B.(b﹣a)
C.a
D.b
20.如图,在?ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
21.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE
(1)求证:BC=CE;
(2)若BC=2,∠ABC=120°,求DE的长.
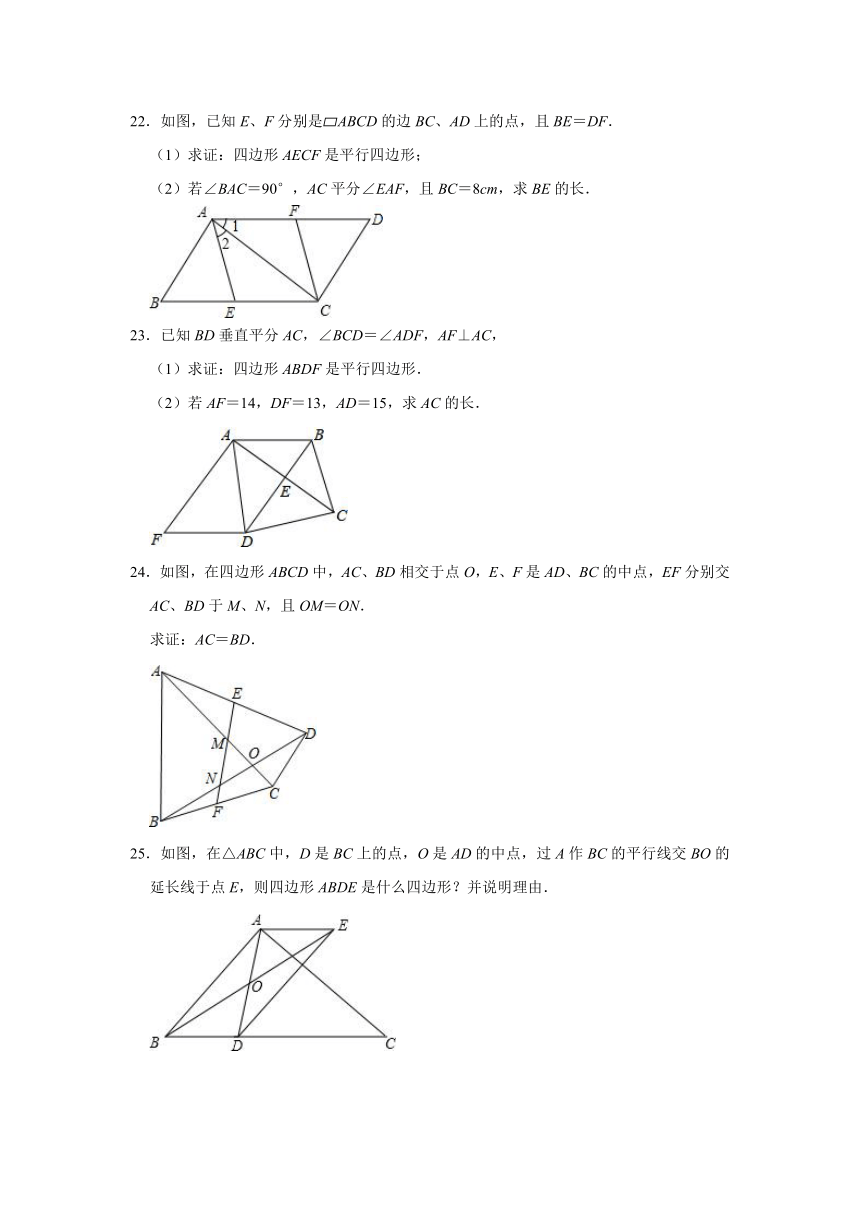
22.如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若∠BAC=90°,AC平分∠EAF,且BC=8cm,求BE的长.
23.已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)求证:四边形ABDF是平行四边形.
(2)若AF=14,DF=13,AD=15,求AC的长.
24.如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,EF分别交AC、BD于M、N,且OM=ON.
求证:AC=BD.
25.如图,在△ABC中,D是BC上的点,O是AD的中点,过A作BC的平行线交BO的延长线于点E,则四边形ABDE是什么四边形?并说明理由.
26.已知AC是?ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,求证:
(1)△ADN≌△CBM;
(2)连接DB,则DB平分MN.
27.【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.
(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为
.
28.如图,分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE,等边△ABD,取AB的中点F,连接DF、EF,已知∠BAC=30°.
(1)求证:四边形ADFE是平行四边形;
(2)若BD=4,求四边形BCEF的面积.
29.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.
(1)求证:四边形AFCD是平行四边形;
(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.
30.如图,四边形ABCD中,BE⊥AC交AD于点G,DF⊥AC于点F,已知AF=CE,AB=CD.
(1)求证:四边形ABCD是平行四边形;
(2)如果∠GBC=∠BCD,AG=6,GE=2,求AB的长.
参考答案
1.解:∵四边形ABCD是平行四边形,
∴CE=AC,BE=BD,
∵AC⊥BC,
∴∠ACB=90°,
∴AC===12,
∴CE=AC=6,
∴BE===,
∴BD=2BE=2;
故答案为:2.
2.解:∵四边形ABCD是平行四边形,
∴BC=AD,OA=OC,0D=0B,
∵△AOB的周长和△BOC的周长相差3cm,
∴(AB+OA+OB)﹣(OB+OC+BC)=3,
∴AB﹣BC=3,
∵AB=5,
∴AD=BC=2.
故答案为:2.
3.解:根据题意得:PA=t,CQ=2t,则PD=AD﹣PA=12﹣t.
∵PQ∥CD且PQ=CD,
∴四边形PQCD为平行四边形,
即12﹣t=2t,
解得:t=4,
即当t=4时,PQ∥CD且PQ=CD.
故答案为:4.
4.解:∵?ABCD的周长=2(BC+CD)=48,
∴BC+CD=24①,
∵AE⊥BC于E,AF⊥CD于F,AE=5,AF=10,
∴S?ABCD=5BC=10CD,
整理得,BC=2CD②,
联立①②解得,CD=8,
∴?ABCD的面积=CD?AF=8×10=80.
故答案为:80.
5.解:延长BN交AC于D,
∵AN平分∠BAC,BN⊥AN,
∴AD=AB=8cm,BN=ND,
∴DC=AC﹣AD=8cm,
∵M是BC边的中点,BN=ND,
∴MN=DC=4cm,
故答案为:4.
6.解:连接AC,如图所示:
∵四边形ABCD是平行四边形,
∴△ABC的面积=△ADC的面积=平行四边形ABCD的面积,
∵E、F分别是AD、DC的中点,△CEF的面积为3,
∴△DEF的面积=△CEF的面积=3,△ACE的面积=△CDE的面积=3+3=6,
∴△ADC的面积=2△CDE的面积=12,
∴?ABCD的面积=2△ADC的面积=24;
故答案为:24.
7.解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵平行四边形ABCD的周长为24,
∴AD+CD=12,
∵OE⊥AC,
∴AE=CE,
∴△DEC的周长=CD+CE+DE=CD+CE+AE=CD+AD=12.
故答案为:12.
8.解:如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BD,
∴∠DCE=∠BEC,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠BEC=∠BCE,
∴BE=BC,
同理AF=AD=BC,
∵BE+AF=AB+EF,
∴2BC=7+1,
∴BC=4;
故答案为:4.
9.解:∵四边形ABCD是平行四边形,
∴∠BCD=∠A=67°,
∵DB=DC,
∴∠DBC=∠BCD=67°,
∵CE⊥BD,
∴∠CEB=90°,
∴∠BCE=90°﹣67°=23°.
故答案为:23°.
10.解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP==6,
∴△APB的周长=6+8+10=24;
故答案为:24.
11.解:∵四边形ABCD是平行四边形,
∴CD=AB=3,BC=AD=4,AB∥CD,
∴∠GCE=∠B=60°,
∵E是BC的中点,
∴CE=BE=2,
∵EF⊥AB,
∴EF⊥DG,
∴∠G=90°,
∴CG=CE=1,
∴EG=CG=,DG=CD+CG=3+1=4,
∴DE===;
故答案为:.
12.解:设C点的坐标为(x,y),
①当BC=AO时,
∵O(0,0),A(﹣3,0),B(0,2)
∴AO=3,
∴BC=3,
∴C点坐标为C(3,2)或C(﹣3,2)
②BO=AC时,
∵BO=2,∴AC=2,
∴C点坐标为C(﹣3,﹣2);
故答案为:(3,2)或(﹣3,2)或(﹣3,﹣2).
13.解:∵BD平分∠EBC,
∴∠EBD=∠CBD.
又∵AD∥BC,
∴∠EDB=∠DBC.
∴∠EBD=∠EDB.
∴BE=ED.
∴△AEB的周长=AB+AD=×10=5.
故答案为:5.
14.解:在平行四边形ABCD中,∠B=∠D,AD∥BC,
∵∠B+∠D=100°,
∴∠B=50°,
∴∠A=180°﹣∠B=180°﹣50°=130°.
故选:D.
15.解:如图,延长EF,GC两条线相交于点H,过点G作GP∥EF交BC于点P,
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵BF=BE=8,
∴CF=BF﹣BC=2,
∵CE平分∠BEF,
∴∠GEC=∠HEC,
∵CE⊥GC,
∴∠ECG=∠ECH=90°,
在△ECG和△ECH中,
,
∴△ECG≌△ECH(ASA),
∴CG=CH,
∵GP∥EF,
∴∠PGC=∠FHC,
在△PCG和△FCH中,
,
∴△PCG≌△FCH(ASA),
∴CP=CF=2,
∴BP=BF﹣PF=8﹣4=4,
∵BF=BE,
∴∠BEF=∠BFE,
∵GP∥EF,
∴∠BGP=∠BEF,∠BPG=∠BFE,
∴∠BGP=∠BPG,
∴BG=BP=4.
故选:C.
16.解:∵ABCD是平行四边形,∴AD∥BC,AD=BC,AO=CO,OB=OD
∴∠DAC=∠ACB,
∵∠AOE=∠COF
∴△COF≌△AOE(ASA)
∵S△AOE=4,AE=ED
∴S△COF=S△DOE=S△AOE=4,
∴S△AOD=8
∵AO=CO
∴S△COD=S△AOD=8
∴S四边形EFCD=S△DOE+S△COD+S△COF=4+8+4=16;
故选:C.
17.解:∵四边形ABCD是平行四边形,
∴∠BAD=∠C=100°,AD∥BC,
∴∠2=∠ADE,
∵l1∥l2,
∴∠ADE+∠BAD+∠1=180°,
∴∠1+∠2=180°﹣∠BAD=80°;
故选:C.
18.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,即AB∥CE,
∴∠ABF=∠E,
∵DE=CD,
∴AB=DE,
在△ABF和△DEF中,
∵,
∴△ABF≌△DEF(AAS),
∴AF=DF,BF=EF;
可得③⑤正确,
故选:B.
19.解:∵平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,
∴EH=BC,EH∥BC,
∴∠EHO=∠CBO,
在△EHO与△CBO中,,
∴△EHO≌△CBO(AAS),
∴△EHO面积=△CBO面积,
∴S阴影=S△EGH=S?EFGH=b;
故选:D
20.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABE=∠FCE,
∵E为BC中点,
∴BE=CE,
在△ABE与△FCE中,
,
∴△ABE≌△FCE(ASA),
∴AB=CF;
(2)∵AD=2AB,AB=FC=CD,
∴AD=DF,
∵△ABE≌△FCE,
∴AE=EF,
∴DE⊥AF.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠FEC,∠ADF=∠ECF,
∵点F为边DC的中点,
∴DF=CF,
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS),
∴AD=CE,
∴BC=CE.
(2)解:如图,连接FM,
∵DM平分∠ADF,AF平分∠DAB,AB∥DC,AD∥BC,
∴∠DAF=∠BAF=DFN,∠ADM=∠FDM=∠AMD,
∴AD=DF=AM,
∴四边形AMFD是菱形,
∴AM=AD=AD=BC=2,AF⊥DM,DN=MN=DM,AN=FN,∵∠ABC=120°,
∴∠BAD=60°,
∴△ADM是等边三角形,
∴DM=AD=2,
∴DN=1,
∴FN=DN==,
∴AF=2,
∵AD=CE,AD∥CE,
∴EF:AF=CE:AD=1:1,
∴EF=AF=2,
∴EN=FN+EF=3,
在Rt△DEN中,DE===2.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴AF∥EC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形.
(2)解:∵AC平分∠EAF,
∴∠1=∠2,
∵AD∥BC,
∴∠1=∠ACE,
∴∠2=∠ACE,
∴AE=CE,
∵∠BAC=90°,
∴∠BAE=90°﹣∠1,∠B=90°﹣∠ACE,
∴∠BAE=∠B,
∴AE=BE,
∴BE=AE=CE=BC=4cm.
23.(1)证明:∵BD垂直平分AC,
∴AB=BC,AD=DC,
在△ADB与△CDB中,
,
∴△ADB≌△CDB(SSS)
∴∠BCD=∠BAD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,
∴BD=AF=14,AB=DF=13,
设BE=x,则DE=14﹣x,由勾股定理得:
∴AB2﹣BE2=AD2﹣DE2,
即132﹣x2=152﹣(14﹣x)2
解得:x=5,
即BE=5,
∴AE===12,
∴AC=2AE=24.
24.证明:取AB和CD的中点分别为G、H,连接EG、GF、FH、EH,
则EH∥AC,EH=AC,HF∥BD,FH=BD,
∴∠3=∠2,∠1=∠4,
∵OM=ON,
∴∠1=∠2,
∴∠4=∠3=∠1=∠2,
同理∠EFH=∠GFE=∠1=∠2,
∴∠4=∠EFH,
∴EH=HF,
∵EH=AC,FH=BD,
∴AC=BD.
25.四边形ABDE是平行四边形,
理由是:∵AE∥BC,
∴∠EAO=∠ODB,∠AEO=∠DBO,
∵O是AD的中点,
∴AO=OD,
∵在△AOE和△DOB中
∵,
∴△AOE≌△DOB,
∴OB=OE,
∵AO=OD,
∴四边形ABDE是平行四边形.
26.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAC=∠BCA,
∵BM⊥AC,DN⊥AC,
∴∠AND=∠BMC=90°,
∵在△ADN和△CBM中
∵,
∴△ADN≌△CBM.
(2)证明:∵△ADN≌△CBM,
∴DN=BM,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形DNBM是平行四边形,
∴OM=ON,
即DB平分MN.
27.【教材呈现】证明:∵P是BD的中点,M是DC的中点,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM,
【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,
∴PM∥BC,
∴∠PMN=∠F,
同理,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(2)解:∵PN∥AD,
∴∠PNB=∠A,
∵∠DPN是△PNB的一个外角,
∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,
∵PM∥BC,
∴∠MPD=∠DBC,
∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,
∵PM=PN,
∴∠PMN=×(180°﹣122°)=29°,
∴∠F=∠PMN=29°,
故答案为:29°.
28.(1)证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABD是等边三角形,F是AB的中点,
∴AD=AB=BD,AB=2AF,DF⊥AB,
∴AF=BC,
在Rt△AFD和Rt△BCA中,
,
∴Rt△AFD≌Rt△BCA(HL),
∴DF=AC,
∵△ACE是等边三角形,
∴∠EAC=60°,AC=AE,
∴∠EAB=∠EAC+∠BAC=90°,
∴DF=AE,
又∵DF⊥AB,
∴DF∥AE,
∴四边形ADFE是平行四边形;
(2)解:由(1)得:△AEF的面积=△ADF的面积=△ABC的面积,AB=BD=4,BC=AB=2,AC=BC=2,
∴四边形BCEF的面积=△ACE的面积+△ABC的面积﹣△AEF的面积=△ACE的面积=×(2)2=3.
29.(1)证明:∵E是AC的中点,
∴AE=CE,
∵CD∥AB,
∴∠AFE=∠CDE,
在△AEF和△CED中,
,
∵∴△AEF≌△CED(AAS),
∴AF=CD,
又∵CD∥AB,即AF∥CD,
∴四边形AFCD是平行四边形;
(2)解:过C作CM⊥AB于M,如图所示:
则∠CMB=∠CMA=90°,
∵CD∥AB,
∴∠B+∠DCB=180°,
∴∠B=180°﹣135°=45°,
∴△BCM是等腰直角三角形,
∴BM=CM,
∵∠BAC=60°,
∴∠ACM=30°,
∴AC=2AM,BM=CM=AM,
∵AM+BM=AB,
∴AM+AM=6,
解得:AM=3﹣3,
∴AC=2AM=6﹣6.
30.(1)证明:∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
∵AF=CE,
∴AF﹣EF=CE﹣EF,
即AE=CF,
在Rt△ABE和Rt△CDF中,,
∴Rt△ABE≌Rt△CDF(HL),
∴∠BAE=∠DCF,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形;
(2)解:由(1)得:四边形ABCD是平行四边形,
∴AD∥BC,
∴DG∥BC,
∵∠GBC=∠BCD,
∴四边形BCDG是等腰梯形,
∴BG=CD=AB,
∵AE===4,
设AB=BG=x,则BE=x﹣2,
在Rt△ABE中,由勾股定理得:(4)2+(x﹣2)2=x2,
解得:x=9,
∴AB=9.
1.如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=5,AB=13,则BD的长是
.
2.?ABCD的对角线AC,BD相交于点O.已知AB=5cm,△AOB的周长和△BOC的周长相差3cm,则AD的长为
.
3.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=6cm,AD=12cm,BC=15CM.点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以2cm/s的速度向点B运动,规定其t=
s时,PQ∥CD且PQ=CD.
4.如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是
.
5.如图,△ABC中,已知M是BC边的中点,AN平分∠BAC,BN⊥AN,若AB=8cm,AC=16cm,则MN=
cm.
6.如图,在?ABCD中,E、F分别是AD、DC的中点,若△CEF的面积为3,则?ABCD的面积为
.
7.平行四边形ABCD的周长为24,对角线AC、BD相交于点O,作OE⊥AC,交AD与点E,连接CE,那么△DEC的周长为
.
8.已知?ABCD中,AB=7,∠ADC与∠BCD的平分线分别交边AB于点F、E,若EF=1,则BC的长为
.
9.如图,在?ABCD中,DB=DC,∠A=67°,CE⊥BD于点E,则∠BCE=
.
10.如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是
.
11.如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=
.
12.在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是O(0,0),A(﹣3,0),B(0,2),则平行四边形第四个顶点C的坐标
.
13.如图,在?ABCD中,点E在AD上,BD平分∠EBC.若?ABCD的周长为10,则△AEB的周长为
.
14.如图,在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
A.50°
B.65°
C.100°
D.130°
15.如图,在平行四边形ABCD中,AD=6,点E在边AD上,点F在BC的延长线上,且满足BF=BE=8,过点C作CE的垂线交BE于点G,若CE恰好平分∠BEF,则BG的长为( )
A.2
B.3
C.4
D.2
16.如图,过平行四边形ABCD对角线交点O的线段EF,分别交AD,BC于点E,F,当AE=ED时,△AOE的面积为4,则四边形EFCD的面积是( )
A.8
B.12
C.16
D.32
17.如图,l1∥l2,?ABCD的顶点A在l1上,BC交l2于点E.若∠C=100°,则∠1+∠2=( )
A.100°
B.90°
C.80°
D.70°
18.如图,在平行四边形ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.下列结论,其中正确的有( )个.
①DE=DF;②AG=GF;③AF=DF;④BG=GC;⑤BF=EF.
A.1
B.2
C.3
D.4
19.如图,平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,CE交GH于点O,已知S?ABCD=a,S?EFGH=b(a<b),则S阴影为( )
A.b﹣a
B.(b﹣a)
C.a
D.b
20.如图,在?ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
21.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE
(1)求证:BC=CE;
(2)若BC=2,∠ABC=120°,求DE的长.
22.如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若∠BAC=90°,AC平分∠EAF,且BC=8cm,求BE的长.
23.已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)求证:四边形ABDF是平行四边形.
(2)若AF=14,DF=13,AD=15,求AC的长.
24.如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,EF分别交AC、BD于M、N,且OM=ON.
求证:AC=BD.
25.如图,在△ABC中,D是BC上的点,O是AD的中点,过A作BC的平行线交BO的延长线于点E,则四边形ABDE是什么四边形?并说明理由.
26.已知AC是?ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,求证:
(1)△ADN≌△CBM;
(2)连接DB,则DB平分MN.
27.【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.
(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为
.
28.如图,分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE,等边△ABD,取AB的中点F,连接DF、EF,已知∠BAC=30°.
(1)求证:四边形ADFE是平行四边形;
(2)若BD=4,求四边形BCEF的面积.
29.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.
(1)求证:四边形AFCD是平行四边形;
(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.
30.如图,四边形ABCD中,BE⊥AC交AD于点G,DF⊥AC于点F,已知AF=CE,AB=CD.
(1)求证:四边形ABCD是平行四边形;
(2)如果∠GBC=∠BCD,AG=6,GE=2,求AB的长.
参考答案
1.解:∵四边形ABCD是平行四边形,
∴CE=AC,BE=BD,
∵AC⊥BC,
∴∠ACB=90°,
∴AC===12,
∴CE=AC=6,
∴BE===,
∴BD=2BE=2;
故答案为:2.
2.解:∵四边形ABCD是平行四边形,
∴BC=AD,OA=OC,0D=0B,
∵△AOB的周长和△BOC的周长相差3cm,
∴(AB+OA+OB)﹣(OB+OC+BC)=3,
∴AB﹣BC=3,
∵AB=5,
∴AD=BC=2.
故答案为:2.
3.解:根据题意得:PA=t,CQ=2t,则PD=AD﹣PA=12﹣t.
∵PQ∥CD且PQ=CD,
∴四边形PQCD为平行四边形,
即12﹣t=2t,
解得:t=4,
即当t=4时,PQ∥CD且PQ=CD.
故答案为:4.
4.解:∵?ABCD的周长=2(BC+CD)=48,
∴BC+CD=24①,
∵AE⊥BC于E,AF⊥CD于F,AE=5,AF=10,
∴S?ABCD=5BC=10CD,
整理得,BC=2CD②,
联立①②解得,CD=8,
∴?ABCD的面积=CD?AF=8×10=80.
故答案为:80.
5.解:延长BN交AC于D,
∵AN平分∠BAC,BN⊥AN,
∴AD=AB=8cm,BN=ND,
∴DC=AC﹣AD=8cm,
∵M是BC边的中点,BN=ND,
∴MN=DC=4cm,
故答案为:4.
6.解:连接AC,如图所示:
∵四边形ABCD是平行四边形,
∴△ABC的面积=△ADC的面积=平行四边形ABCD的面积,
∵E、F分别是AD、DC的中点,△CEF的面积为3,
∴△DEF的面积=△CEF的面积=3,△ACE的面积=△CDE的面积=3+3=6,
∴△ADC的面积=2△CDE的面积=12,
∴?ABCD的面积=2△ADC的面积=24;
故答案为:24.
7.解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵平行四边形ABCD的周长为24,
∴AD+CD=12,
∵OE⊥AC,
∴AE=CE,
∴△DEC的周长=CD+CE+DE=CD+CE+AE=CD+AD=12.
故答案为:12.
8.解:如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BD,
∴∠DCE=∠BEC,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠BEC=∠BCE,
∴BE=BC,
同理AF=AD=BC,
∵BE+AF=AB+EF,
∴2BC=7+1,
∴BC=4;
故答案为:4.
9.解:∵四边形ABCD是平行四边形,
∴∠BCD=∠A=67°,
∵DB=DC,
∴∠DBC=∠BCD=67°,
∵CE⊥BD,
∴∠CEB=90°,
∴∠BCE=90°﹣67°=23°.
故答案为:23°.
10.解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP==6,
∴△APB的周长=6+8+10=24;
故答案为:24.
11.解:∵四边形ABCD是平行四边形,
∴CD=AB=3,BC=AD=4,AB∥CD,
∴∠GCE=∠B=60°,
∵E是BC的中点,
∴CE=BE=2,
∵EF⊥AB,
∴EF⊥DG,
∴∠G=90°,
∴CG=CE=1,
∴EG=CG=,DG=CD+CG=3+1=4,
∴DE===;
故答案为:.
12.解:设C点的坐标为(x,y),
①当BC=AO时,
∵O(0,0),A(﹣3,0),B(0,2)
∴AO=3,
∴BC=3,
∴C点坐标为C(3,2)或C(﹣3,2)
②BO=AC时,
∵BO=2,∴AC=2,
∴C点坐标为C(﹣3,﹣2);
故答案为:(3,2)或(﹣3,2)或(﹣3,﹣2).
13.解:∵BD平分∠EBC,
∴∠EBD=∠CBD.
又∵AD∥BC,
∴∠EDB=∠DBC.
∴∠EBD=∠EDB.
∴BE=ED.
∴△AEB的周长=AB+AD=×10=5.
故答案为:5.
14.解:在平行四边形ABCD中,∠B=∠D,AD∥BC,
∵∠B+∠D=100°,
∴∠B=50°,
∴∠A=180°﹣∠B=180°﹣50°=130°.
故选:D.
15.解:如图,延长EF,GC两条线相交于点H,过点G作GP∥EF交BC于点P,
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵BF=BE=8,
∴CF=BF﹣BC=2,
∵CE平分∠BEF,
∴∠GEC=∠HEC,
∵CE⊥GC,
∴∠ECG=∠ECH=90°,
在△ECG和△ECH中,
,
∴△ECG≌△ECH(ASA),
∴CG=CH,
∵GP∥EF,
∴∠PGC=∠FHC,
在△PCG和△FCH中,
,
∴△PCG≌△FCH(ASA),
∴CP=CF=2,
∴BP=BF﹣PF=8﹣4=4,
∵BF=BE,
∴∠BEF=∠BFE,
∵GP∥EF,
∴∠BGP=∠BEF,∠BPG=∠BFE,
∴∠BGP=∠BPG,
∴BG=BP=4.
故选:C.
16.解:∵ABCD是平行四边形,∴AD∥BC,AD=BC,AO=CO,OB=OD
∴∠DAC=∠ACB,
∵∠AOE=∠COF
∴△COF≌△AOE(ASA)
∵S△AOE=4,AE=ED
∴S△COF=S△DOE=S△AOE=4,
∴S△AOD=8
∵AO=CO
∴S△COD=S△AOD=8
∴S四边形EFCD=S△DOE+S△COD+S△COF=4+8+4=16;
故选:C.
17.解:∵四边形ABCD是平行四边形,
∴∠BAD=∠C=100°,AD∥BC,
∴∠2=∠ADE,
∵l1∥l2,
∴∠ADE+∠BAD+∠1=180°,
∴∠1+∠2=180°﹣∠BAD=80°;
故选:C.
18.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,即AB∥CE,
∴∠ABF=∠E,
∵DE=CD,
∴AB=DE,
在△ABF和△DEF中,
∵,
∴△ABF≌△DEF(AAS),
∴AF=DF,BF=EF;
可得③⑤正确,
故选:B.
19.解:∵平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,
∴EH=BC,EH∥BC,
∴∠EHO=∠CBO,
在△EHO与△CBO中,,
∴△EHO≌△CBO(AAS),
∴△EHO面积=△CBO面积,
∴S阴影=S△EGH=S?EFGH=b;
故选:D
20.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABE=∠FCE,
∵E为BC中点,
∴BE=CE,
在△ABE与△FCE中,
,
∴△ABE≌△FCE(ASA),
∴AB=CF;
(2)∵AD=2AB,AB=FC=CD,
∴AD=DF,
∵△ABE≌△FCE,
∴AE=EF,
∴DE⊥AF.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠FEC,∠ADF=∠ECF,
∵点F为边DC的中点,
∴DF=CF,
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS),
∴AD=CE,
∴BC=CE.
(2)解:如图,连接FM,
∵DM平分∠ADF,AF平分∠DAB,AB∥DC,AD∥BC,
∴∠DAF=∠BAF=DFN,∠ADM=∠FDM=∠AMD,
∴AD=DF=AM,
∴四边形AMFD是菱形,
∴AM=AD=AD=BC=2,AF⊥DM,DN=MN=DM,AN=FN,∵∠ABC=120°,
∴∠BAD=60°,
∴△ADM是等边三角形,
∴DM=AD=2,
∴DN=1,
∴FN=DN==,
∴AF=2,
∵AD=CE,AD∥CE,
∴EF:AF=CE:AD=1:1,
∴EF=AF=2,
∴EN=FN+EF=3,
在Rt△DEN中,DE===2.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴AF∥EC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形.
(2)解:∵AC平分∠EAF,
∴∠1=∠2,
∵AD∥BC,
∴∠1=∠ACE,
∴∠2=∠ACE,
∴AE=CE,
∵∠BAC=90°,
∴∠BAE=90°﹣∠1,∠B=90°﹣∠ACE,
∴∠BAE=∠B,
∴AE=BE,
∴BE=AE=CE=BC=4cm.
23.(1)证明:∵BD垂直平分AC,
∴AB=BC,AD=DC,
在△ADB与△CDB中,
,
∴△ADB≌△CDB(SSS)
∴∠BCD=∠BAD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,
∴BD=AF=14,AB=DF=13,
设BE=x,则DE=14﹣x,由勾股定理得:
∴AB2﹣BE2=AD2﹣DE2,
即132﹣x2=152﹣(14﹣x)2
解得:x=5,
即BE=5,
∴AE===12,
∴AC=2AE=24.
24.证明:取AB和CD的中点分别为G、H,连接EG、GF、FH、EH,
则EH∥AC,EH=AC,HF∥BD,FH=BD,
∴∠3=∠2,∠1=∠4,
∵OM=ON,
∴∠1=∠2,
∴∠4=∠3=∠1=∠2,
同理∠EFH=∠GFE=∠1=∠2,
∴∠4=∠EFH,
∴EH=HF,
∵EH=AC,FH=BD,
∴AC=BD.
25.四边形ABDE是平行四边形,
理由是:∵AE∥BC,
∴∠EAO=∠ODB,∠AEO=∠DBO,
∵O是AD的中点,
∴AO=OD,
∵在△AOE和△DOB中
∵,
∴△AOE≌△DOB,
∴OB=OE,
∵AO=OD,
∴四边形ABDE是平行四边形.
26.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAC=∠BCA,
∵BM⊥AC,DN⊥AC,
∴∠AND=∠BMC=90°,
∵在△ADN和△CBM中
∵,
∴△ADN≌△CBM.
(2)证明:∵△ADN≌△CBM,
∴DN=BM,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形DNBM是平行四边形,
∴OM=ON,
即DB平分MN.
27.【教材呈现】证明:∵P是BD的中点,M是DC的中点,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM,
【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,
∴PM∥BC,
∴∠PMN=∠F,
同理,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(2)解:∵PN∥AD,
∴∠PNB=∠A,
∵∠DPN是△PNB的一个外角,
∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,
∵PM∥BC,
∴∠MPD=∠DBC,
∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,
∵PM=PN,
∴∠PMN=×(180°﹣122°)=29°,
∴∠F=∠PMN=29°,
故答案为:29°.
28.(1)证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABD是等边三角形,F是AB的中点,
∴AD=AB=BD,AB=2AF,DF⊥AB,
∴AF=BC,
在Rt△AFD和Rt△BCA中,
,
∴Rt△AFD≌Rt△BCA(HL),
∴DF=AC,
∵△ACE是等边三角形,
∴∠EAC=60°,AC=AE,
∴∠EAB=∠EAC+∠BAC=90°,
∴DF=AE,
又∵DF⊥AB,
∴DF∥AE,
∴四边形ADFE是平行四边形;
(2)解:由(1)得:△AEF的面积=△ADF的面积=△ABC的面积,AB=BD=4,BC=AB=2,AC=BC=2,
∴四边形BCEF的面积=△ACE的面积+△ABC的面积﹣△AEF的面积=△ACE的面积=×(2)2=3.
29.(1)证明:∵E是AC的中点,
∴AE=CE,
∵CD∥AB,
∴∠AFE=∠CDE,
在△AEF和△CED中,
,
∵∴△AEF≌△CED(AAS),
∴AF=CD,
又∵CD∥AB,即AF∥CD,
∴四边形AFCD是平行四边形;
(2)解:过C作CM⊥AB于M,如图所示:
则∠CMB=∠CMA=90°,
∵CD∥AB,
∴∠B+∠DCB=180°,
∴∠B=180°﹣135°=45°,
∴△BCM是等腰直角三角形,
∴BM=CM,
∵∠BAC=60°,
∴∠ACM=30°,
∴AC=2AM,BM=CM=AM,
∵AM+BM=AB,
∴AM+AM=6,
解得:AM=3﹣3,
∴AC=2AM=6﹣6.
30.(1)证明:∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
∵AF=CE,
∴AF﹣EF=CE﹣EF,
即AE=CF,
在Rt△ABE和Rt△CDF中,,
∴Rt△ABE≌Rt△CDF(HL),
∴∠BAE=∠DCF,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形;
(2)解:由(1)得:四边形ABCD是平行四边形,
∴AD∥BC,
∴DG∥BC,
∵∠GBC=∠BCD,
∴四边形BCDG是等腰梯形,
∴BG=CD=AB,
∵AE===4,
设AB=BG=x,则BE=x﹣2,
在Rt△ABE中,由勾股定理得:(4)2+(x﹣2)2=x2,
解得:x=9,
∴AB=9.
