2020-2021学年人教版八年级数学下册18.1平行四边形经典好题专题提升训练(Word版,附答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册18.1平行四边形经典好题专题提升训练(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 318.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 00:07:50 | ||
图片预览



文档简介
2020-2021年度人教版八年级数学下册《18.1平行四边形》经典好题专题提升训练(附答案)
1.如图,在?ABCD中,BE⊥AB交对角线AC于点E.若∠1=20°,则∠2的度数为( )
A.120°
B.100°
C.110°
D.90°
2.如图,在△ABC中,∠C=50°,AC=BC,点D在AC边上,以AB,AD为边作?ABED,则∠E的度数为( )
A.50°
B.55°
C.65°
D.70°
3.?ABCD中,∠A:∠B:∠C:∠D的度数比可能是( )
A.1:1:2:3
B.1:2:1:2
C.1:1:2:2
D.1:2:2:1
4.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.AB∥AD,AO=CO
C.AB=AD,BC=CD
D.AB∥CD,AD=BC
5.如图,在△ABC中,∠C=90°,AB=13,AC=5,D、E分别是AC、AB的中点,则DE的长是( )
A.6.5
B.6
C.5.5
D.
6.如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE、DE,BE⊥DE,AC,BD互相平分.若2AB=BC=4,则BD的值为( )
A.2
B.
C.3
D.4
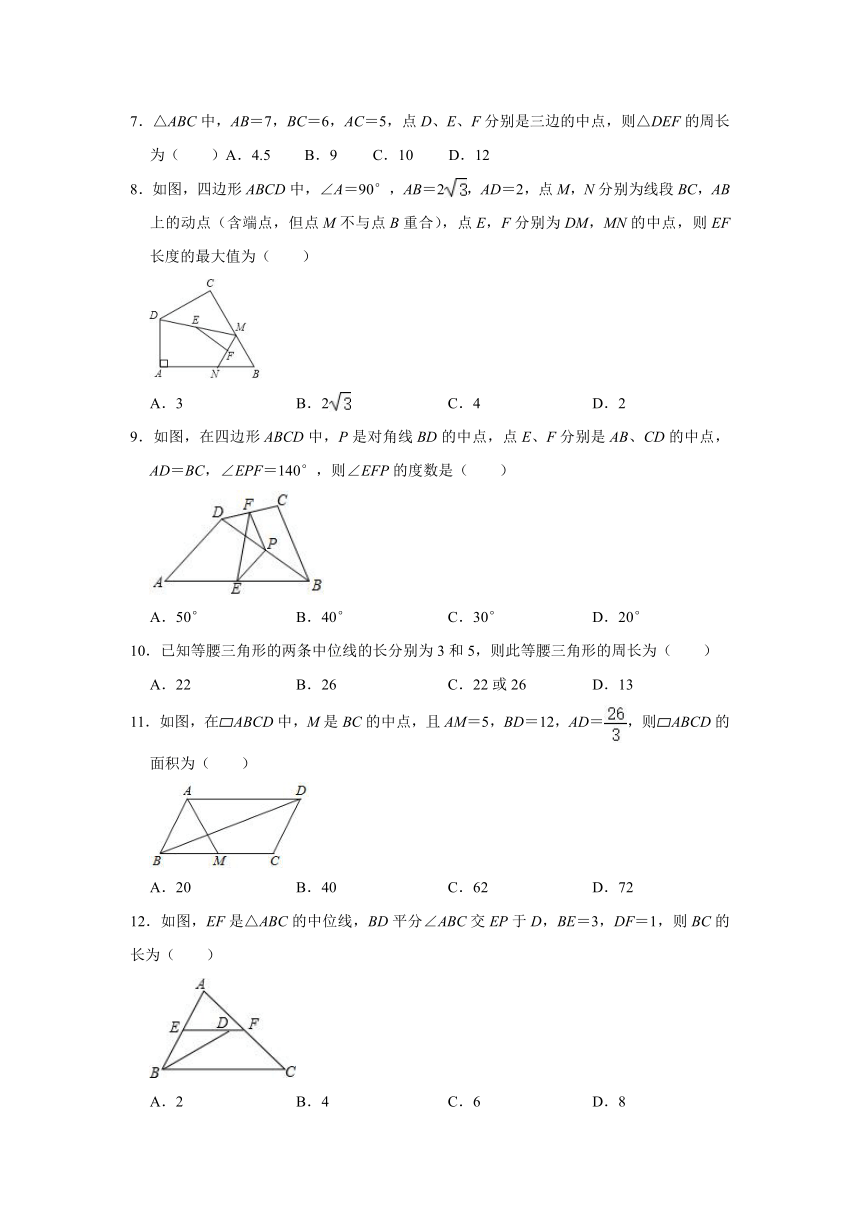
7.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )A.4.5
B.9
C.10
D.12
8.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3
B.2
C.4
D.2
9.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )
A.50°
B.40°
C.30°
D.20°
10.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22
B.26
C.22或26
D.13
11.如图,在?ABCD中,M是BC的中点,且AM=5,BD=12,AD=,则?ABCD的面积为( )
A.20
B.40
C.62
D.72
12.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2
B.4
C.6
D.8
13.已知点A(3,0)、B(﹣1,0)、C(2,3),以A、B、C为顶点画平行四边形,则第四个顶点D的坐标是
.
14.如图,若?ABCD的周长为36cm,过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,?ABCD的面积为
cm2.
15.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是
.
16.?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,则AB的长为
cm.
17.在?ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则对角线BD=
.
18.如图,在平行四边形ABCD中,∠ABC=135°,AD=4,AB=8,作对角线AC的垂直平分线EF,分别交对边AB、CD于点E和点F,则AE的长为
.
19.如图,?ABCD中,AE平分∠BAD,若∠B=52°,则∠AEC的度数为
.
20.如图,在?ABCD中,P为CD上一点,BC=BP,BP平分∠ABC,∠ABD=43°,则∠APB的度数是
度.
21.在?ABCD中,AB=4,AD=5,则AC2+BD2的值为
.
22.如图所示,在平行四边形ABCD中,AB=3,BC=4,∠B=60°,E是BC的中点,EF⊥AB于点F,则△DEF的面积为
平方单位.
23.平行四边形ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为
.
24.如图,在平行四边形ABCD中,∠ABC=105°,对角线AC、BD交于点O,∠DAC=30°,AC=4,点P从B点出发,沿着边BC、CD运动到点D停止,在点P运动过程中,若△OPC是直角三角形,则CP的长是
.
25.如图,在?ABCD中,对角线AC与BD相交于点O,点E,F在BD上,且BE=DF,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:AE=CF;
(2)若AC平分∠HAG,判断四边形AGCH的形状,并证明你的结论.
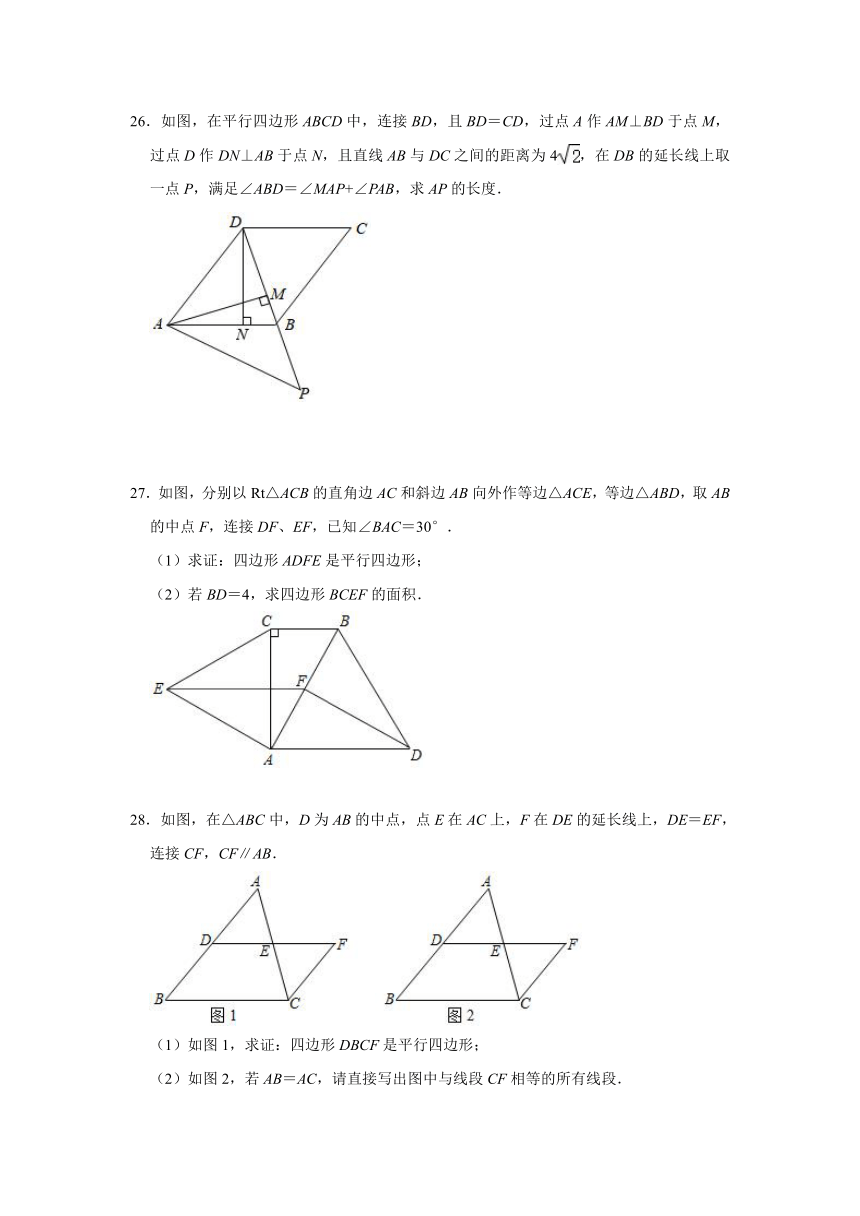
26.如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且直线AB与DC之间的距离为4,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,求AP的长度.
27.如图,分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE,等边△ABD,取AB的中点F,连接DF、EF,已知∠BAC=30°.
(1)求证:四边形ADFE是平行四边形;
(2)若BD=4,求四边形BCEF的面积.
28.如图,在△ABC中,D为AB的中点,点E在AC上,F在DE的延长线上,DE=EF,连接CF,CF∥AB.
(1)如图1,求证:四边形DBCF是平行四边形;
(2)如图2,若AB=AC,请直接写出图中与线段CF相等的所有线段.
29.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.
(1)求证:四边形AFCD是平行四边形;
(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.
30.如图,在△ABC中,点D是BC边的中点,点E,F分别在AC,AB上,且DE∥AB,EF∥BC.
(1)求证:CD=EF;
(2)已知∠ABC=60°,连接BE,若BE平分∠ABC,CD=6,求四边形BDEF的周长.
31.如图,等边△ABC的边长是4,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
32.已知:在平行四边形ABCD中,对角线AC与BD相交于点O,点E、F分别为OB、OD的中点,连接AE并延长至点G,使EG=AE,连接CF、CG.
(1)如图1,求证:EG=FC;
(2)如图2,连接BG、OG,在不添加任何辅助线的情况下,请直接写出图中的四个平行四边形,使写出每个平行四边形的面积都等于平行四边形ABCD面积的一半.
参考答案
1.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠CAB=∠1=20°,
∵BE⊥AB,
∴∠ABE=90°,
∴∠2=∠EAB+∠EBA=20°+90°=110°.
故选:C.
2.解:∵∠C=50°,AC=BC,
∴∠A=∠ABC=(180°﹣50°)=65°,
∵四边形ABED是平行四边形,
∴∠E=∠A=65°.
故选:C.
3.解:根据平行四边形的两组对角分别相等,可知B正确.
故选:B.
4.解:能判定四边形ABCD是平行四边形的是∠A=∠C,∠B=∠D,理由如下:
∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,
故选:A.
5.解:在△ABC中,∠C=90°,AB=13,AC=5,
则BC===12,
∵D、E分别是AC、AB的中点,
∴DE=BC=6,
故选:B.
6.解:连接OE,如图所示:
∵2AB=BC=4,
∴AB=2,
∵AC,BD互相平分,
∴OA=OC,OB=OD,四边形ABCD是平行四边形,
∵以AC为斜边作Rt△ACE,
∴OE=OA=OC=AC,
∵BE⊥DE,
∴OE=OB=OD=BD,
∴AC=BD,
∴四边形ABCD是矩形,
∴AD=BC=4,∠BAD=90°,
∴BD===2,
故选:A.
7.解:∵点D、E、F分别是三边的中点,
∴DE、EF、DF为△ABC的中位线,
∴DE=AB=×7=,DF=AC=×5=,EF=BC=×6=3,
∴△DEF的周长=++3=9,
故选:B.
8.解:连接DN、DB,
在Rt△DAB中,∠A=90°,AB=2,AD=2,
∴BD==4,
∵点E,F分别为DM,MN的中点,
∴EF=DN,
由题意得,当点N与点B重合是DN最大,最大值为4,
∴EF长度的最大值为2,
故选:D.
9.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠EFP=×(180°﹣∠EPF)=×(180°﹣140°)=20°,
故选:D.
10.解:等腰三角形的两条中位线长分别为3和5,
根据三角形中位线定理可知,等腰三角形的两边长为6和10,
当腰为10时,则三边长为10,10,6时,周长为26;
当腰为6时,则三边长为6,6,10时,周长为22,
故选:C.
11.解:过D作DE∥AM交BC的延长线于E.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵DE∥AM,
∴四边形AMED是平行四边形,
∴AD=ME,AM=DE,
∵M是BC的中点,AD=,
∴MB=BC=,
∴BE=BM+ME=13,
∵四边形AMED是平行四边形,
∴AM=DE=5,
∵BD=12,
∴52+122=132,
∴△DBE为直角三角形.
∴BE边上的高为
=,
∴平行四边形ABCD的面积为×=40.
故选:B.
12.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵EF是△ABC的中位线,
∴EF∥BC,BC=2EF,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴ED=EB=3,
∴EF=ED+DF=4,
∴BC=2EF=8,故选:D.
13.解:如图,
以BC为对角线,将AB向上平移3个单位,再向左平移1个单位,B点对应的位置为(﹣2,3)就是第四个顶点D1;
以AB为对角线,将BC向下平移3个单位,再向右平移1个单位,B点对应的位置为(0,﹣3)就是第四个顶点D2′;
以AC为对角线,将AB向上平移3个单位,再向右平移4个单位,C点对应的位置为(7,3)就是第四个顶点D3;
∴第四个顶点D的坐标为:(﹣2,3)或(0,﹣3)或(7,3),
故答案为:(﹣2,3)或(0,﹣3)或(7,3).
14.解:∵?ABCD的周长为36cm,
∴AB+BC=18cm①,
∵过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,
∴4AB=5BC②,
由①②得:AB=10cm,BC=8cm,
∴?ABCD的面积为:AB?DE=40(cm2).
故答案为:40.
15.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故答案为:S1=S2.
16.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD,
又平行四边形ABCD的周长为60cm,△AOB的周长比△BOC的周长长8cm,
∴,
两个方程相加,得AB=19(cm).
故答案为:19.
17.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵AB⊥AC,
∴∠BAC=90°,
∴AC===2,
∴OA=AC=,
∴OB===,
∴BD=2OB=2;
故答案为:2.
18.解:如图,连接CE,过点C作CH⊥AB,交AB的延长线于H,
∵平行四边形ABCD中,∠ABC=135°,AD=4,
∴∠CBH=45°,BC=4,
又∵∠H=90°,
∴∠BCH=45°,
∴CH=BH=4,
设AE=x,则BE=8﹣x,
∵EF垂直平分AC,
∴CE=AE=x,
∵在Rt△CEH中,CH2+EH2=EC2,
∴42+(8﹣x+4)2=x2,
解得x=,
∴AE的长为.
故答案为:.
19.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BAD+∠B=180°,∠DAE=∠AEB,
∴∠BAD=180°﹣∠B=180°﹣52°=128°,
∵AE平分∠BAD,
∴∠AEB=∠DAE=∠BAD=64°,
∴∠AEC=180°﹣∠AEB=180°﹣64°=116°;
故答案为:116°.
20.证明:∵ABCD是平行四边形,
∴AB∥DC,AD=BC,
∴∠ABP=∠BPC,
∵BP平分∠ABC,
∴∠ABP=∠CBP,
∴∠BPC=∠CBP,
∵BC=BP,
∴∠BPC=∠C,
∴∠CBP=∠BPC=∠C,
∴BC=BP=PC,
∴△BPC是等边三角形,
∴∠BPC=∠PBC=∠ABP=∠BAD=60°,
∴四边形DPBA是等腰梯形,
∴∠PAB=∠ABD=43°,
∴∠APB=180°﹣60°﹣43°=77°.
故答案为:77.
21.解:过点A作AE⊥BC于E,过点D作DF⊥BC于F,
设BE=CF=x,AE=DF=y,
则
AC2+BD2=(5﹣x)2+y2+(5+x)2+y2=50+2x2+2y2=50+2×42=82.
故答案为:82.
22.解:如图,延长DC和FE交于点G,
在平行四边形ABCD中,AB∥CD,
∴∠B=∠ECG,
∵E为BC的中点,
∴BE=CE=BC=×4=2,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(ASA),
∴BF=CG,
∵∠B=60°,
∴∠FEB=30°,
∴BF=BE=1,
∴EF=,
∵CG=BF=1,CD=AB=3,
∴DG=CD+CG=3+1=4,
∵EF⊥AB,AB∥CD,
∴DG⊥FG,
∴S△DEF=EF?DG=××4=2.
故答案为:2.
23.解:如图,过点A作AE⊥BC于点E、AF⊥CD于点F.
由题意得,S四边形ABCD=AE×BC=CD×AF,
∵AB=12,BC=26,AE=8,
∴26×8=12×AF,
∴AF=,
即AB与CD间的距离为.
故答案是:.
24.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC=2,AB∥CD,AD∥BC,
∴∠OCD=∠BAC,∠BCO=∠DAC=30°,∠BAD=180°﹣∠ABC=180°﹣105°=75°,
∴∠OCD=∠BAC=75°﹣30°=45°,
分三种情况:
①当点P在BC上,∠POC=90°时,如图1所示:
∵∠BCO=30°,
∴OP=OC=,CP=2OP=;
②当点P在BC上,∠OPC=90°时,如图2所示:
∵∠BCO=30°,
∴OP=OC=1,CP=OP=;
③当点P在CD上,∠OPC=90°时,如图3所示:
∵∠OCD=45°,
∴△OPC是等腰直角三角形,
∴CP=OC=;
综上所述,若△OPC是直角三角形,则CP的长是或或,
故答案为:或或.
25.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)四边形AGCH是菱形.理由如下:
∵△AOE≌△COF,
∴∠EAO=∠FCO,
∴AG∥CH,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形AGCH是平行四边形,
∵AD∥BC,
∴∠HAC=∠ACB,
∵AC平分∠HAG,
∴∠HAC=∠GAC,
∵∠GAC=∠ACB,
∴GA=GC,
∴平行四边形AGCH是菱形.
26.解:在平行四边形ABCD中,AB=CD,
∵BD=CD,
∴BD=BA,
又∵AM⊥BD,DN⊥AB,
∴DN=AM=4,
又∵∠ABD=∠MAP+∠PAB,∠ABD=∠P+∠BAP,
∴∠P=∠PAM,
∴△APM是等腰直角三角形,
∴AP=AM=8.
27.(1)证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABD是等边三角形,F是AB的中点,
∴AD=AB=BD,AB=2AF,DF⊥AB,
∴AF=BC,
在Rt△AFD和Rt△BCA中,
,
∴Rt△AFD≌Rt△BCA(HL),
∴DF=AC,
∵△ACE是等边三角形,
∴∠EAC=60°,AC=AE,
∴∠EAB=∠EAC+∠BAC=90°,
∴DF=AE,
又∵DF⊥AB,
∴DF∥AE,
∴四边形ADFE是平行四边形;
(2)解:由(1)得:△AEF的面积=△ADF的面积=△ABC的面积,AB=BD=4,BC=AB=2,AC=BC=2,
∴四边形BCEF的面积=△ACE的面积+△ABC的面积﹣△AEF的面积=△ACE的面积=×(2)2=3.
28.(1)证明:∵CF∥AB,
∴∠A=∠ECF,
又∵∠AED=∠CEF,DE=FE,
∴△ADE≌△CFE(AAS),
∴AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,且CF∥BD,
∴四边形DBCF是平行四边形;
(2)解:与线段CF相等的所有线段为AD、BD、AE、CE;理由如下:
由(1)得:BD=AD=CF,AE=CE,
∵AB=AC,
∴BD=AD=AE=CE=CF.
29.(1)证明:∵E是AC的中点,
∴AE=CE,
∵CD∥AB,
∴∠AFE=∠CDE,
在△AEF和△CED中,
,
∵∴△AEF≌△CED(AAS),
∴AF=CD,
又∵CD∥AB,即AF∥CD,
∴四边形AFCD是平行四边形;
(2)解:过C作CM⊥AB于M,如图所示:
则∠CMB=∠CMA=90°,
∵CD∥AB,
∴∠B+∠DCB=180°,
∴∠B=180°﹣135°=45°,
∴△BCM是等腰直角三角形,
∴BM=CM,
∵∠BAC=60°,
∴∠ACM=30°,
∴AC=2AM,BM=CM=AM,
∵AM+BM=AB,
∴AM+AM=6,
解得:AM=3﹣3,
∴AC=2AM=6﹣6.
30.(1)证明:∵DE∥AB,EF∥BC,
∴四边形BDEF是平行四边形,
∴EF=BD,
∵点D是BC边的中点,
∴BD=CD,
∴CD=EF;
(2)解:∵BE平分∠ABC,
∴∠FBE=∠DBE,
又∵四边形BDEF是平行四边形,
∴BD=EF,BF=ED,EF∥BD,
∴∠FEB=∠DBE,
∴∠FBE=∠BEF,
∴BF=EF,
∴BD=EF=BF=ED,
又∵BD=CD=6,
∴BD=EF=BF=ED=6,
∴四边形BDEF的周长=6×4=24.
31.(1)证明:∵D,E为AB,AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,
∴DE=CF;
(2)解:由(1)可知,DE∥BC,DE=CF,
∴四边形DCFE为平行四边形,
∴EF=DC,
在等边△ABC中,D为AB中点,
∴CD⊥AB,
∴CD=BC?sin60°=2,
∴EF=2.
32.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=FC,
∵EG=AE,
∴EG=FC;
(2)解:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,AB=CD,S四边形ABCD=4S△ABO,
∵EG=AE,点E为OB的中点,
∴AG、OB互相平分,
∴四边形ABGO是平行四边形,
∴S△ABO=S△BGO,
∴S四边形ABGO=2S△ABO=S四边形ABCD,
∵OA=OC,EG=AE,
∴OE是△ACG的中位线,
∴OE∥CG,
∵四边形ABGO是平行四边形,
∴BG∥AC,
∴四边形BOCG是平行四边形,
∴S四边形BGCO=2S△BGO=2S△ABO=S四边形ABCD,
∵四边形ABGO是平行四边形,
∴GO∥AB,GO=AB,
∵AB∥CD,
∴GO∥CD,GO=CD,
∴四边形CDOG是平行四边形,
∴S四边形CDOG=2S△CDO=2S△ABO=S四边形ABCD,
∵点E,F分别为OB,OD的中点,
∴EF=BD=OD,
∵四边形CDOG是平行四边形,
∴CG∥EF,CG=OD,
∴EF=CG,
∴四边形EFCG是平行四边形,
∴S四边形EFCG=S四边形CDOG=S四边形ABCD,
∴图中的平行四边形ABGO、平行四边形BOCG、平行四边形CDOG、平行四边形EFCG四个平行四边形,每个平行四边形的面积都等于平行四边形ABCD面积的一半.
1.如图,在?ABCD中,BE⊥AB交对角线AC于点E.若∠1=20°,则∠2的度数为( )
A.120°
B.100°
C.110°
D.90°
2.如图,在△ABC中,∠C=50°,AC=BC,点D在AC边上,以AB,AD为边作?ABED,则∠E的度数为( )
A.50°
B.55°
C.65°
D.70°
3.?ABCD中,∠A:∠B:∠C:∠D的度数比可能是( )
A.1:1:2:3
B.1:2:1:2
C.1:1:2:2
D.1:2:2:1
4.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.AB∥AD,AO=CO
C.AB=AD,BC=CD
D.AB∥CD,AD=BC
5.如图,在△ABC中,∠C=90°,AB=13,AC=5,D、E分别是AC、AB的中点,则DE的长是( )
A.6.5
B.6
C.5.5
D.
6.如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE、DE,BE⊥DE,AC,BD互相平分.若2AB=BC=4,则BD的值为( )
A.2
B.
C.3
D.4
7.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )A.4.5
B.9
C.10
D.12
8.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3
B.2
C.4
D.2
9.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )
A.50°
B.40°
C.30°
D.20°
10.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22
B.26
C.22或26
D.13
11.如图,在?ABCD中,M是BC的中点,且AM=5,BD=12,AD=,则?ABCD的面积为( )
A.20
B.40
C.62
D.72
12.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2
B.4
C.6
D.8
13.已知点A(3,0)、B(﹣1,0)、C(2,3),以A、B、C为顶点画平行四边形,则第四个顶点D的坐标是
.
14.如图,若?ABCD的周长为36cm,过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,?ABCD的面积为
cm2.
15.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是
.
16.?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,则AB的长为
cm.
17.在?ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则对角线BD=
.
18.如图,在平行四边形ABCD中,∠ABC=135°,AD=4,AB=8,作对角线AC的垂直平分线EF,分别交对边AB、CD于点E和点F,则AE的长为
.
19.如图,?ABCD中,AE平分∠BAD,若∠B=52°,则∠AEC的度数为
.
20.如图,在?ABCD中,P为CD上一点,BC=BP,BP平分∠ABC,∠ABD=43°,则∠APB的度数是
度.
21.在?ABCD中,AB=4,AD=5,则AC2+BD2的值为
.
22.如图所示,在平行四边形ABCD中,AB=3,BC=4,∠B=60°,E是BC的中点,EF⊥AB于点F,则△DEF的面积为
平方单位.
23.平行四边形ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为
.
24.如图,在平行四边形ABCD中,∠ABC=105°,对角线AC、BD交于点O,∠DAC=30°,AC=4,点P从B点出发,沿着边BC、CD运动到点D停止,在点P运动过程中,若△OPC是直角三角形,则CP的长是
.
25.如图,在?ABCD中,对角线AC与BD相交于点O,点E,F在BD上,且BE=DF,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:AE=CF;
(2)若AC平分∠HAG,判断四边形AGCH的形状,并证明你的结论.
26.如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且直线AB与DC之间的距离为4,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,求AP的长度.
27.如图,分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE,等边△ABD,取AB的中点F,连接DF、EF,已知∠BAC=30°.
(1)求证:四边形ADFE是平行四边形;
(2)若BD=4,求四边形BCEF的面积.
28.如图,在△ABC中,D为AB的中点,点E在AC上,F在DE的延长线上,DE=EF,连接CF,CF∥AB.
(1)如图1,求证:四边形DBCF是平行四边形;
(2)如图2,若AB=AC,请直接写出图中与线段CF相等的所有线段.
29.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.
(1)求证:四边形AFCD是平行四边形;
(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.
30.如图,在△ABC中,点D是BC边的中点,点E,F分别在AC,AB上,且DE∥AB,EF∥BC.
(1)求证:CD=EF;
(2)已知∠ABC=60°,连接BE,若BE平分∠ABC,CD=6,求四边形BDEF的周长.
31.如图,等边△ABC的边长是4,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
32.已知:在平行四边形ABCD中,对角线AC与BD相交于点O,点E、F分别为OB、OD的中点,连接AE并延长至点G,使EG=AE,连接CF、CG.
(1)如图1,求证:EG=FC;
(2)如图2,连接BG、OG,在不添加任何辅助线的情况下,请直接写出图中的四个平行四边形,使写出每个平行四边形的面积都等于平行四边形ABCD面积的一半.
参考答案
1.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠CAB=∠1=20°,
∵BE⊥AB,
∴∠ABE=90°,
∴∠2=∠EAB+∠EBA=20°+90°=110°.
故选:C.
2.解:∵∠C=50°,AC=BC,
∴∠A=∠ABC=(180°﹣50°)=65°,
∵四边形ABED是平行四边形,
∴∠E=∠A=65°.
故选:C.
3.解:根据平行四边形的两组对角分别相等,可知B正确.
故选:B.
4.解:能判定四边形ABCD是平行四边形的是∠A=∠C,∠B=∠D,理由如下:
∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,
故选:A.
5.解:在△ABC中,∠C=90°,AB=13,AC=5,
则BC===12,
∵D、E分别是AC、AB的中点,
∴DE=BC=6,
故选:B.
6.解:连接OE,如图所示:
∵2AB=BC=4,
∴AB=2,
∵AC,BD互相平分,
∴OA=OC,OB=OD,四边形ABCD是平行四边形,
∵以AC为斜边作Rt△ACE,
∴OE=OA=OC=AC,
∵BE⊥DE,
∴OE=OB=OD=BD,
∴AC=BD,
∴四边形ABCD是矩形,
∴AD=BC=4,∠BAD=90°,
∴BD===2,
故选:A.
7.解:∵点D、E、F分别是三边的中点,
∴DE、EF、DF为△ABC的中位线,
∴DE=AB=×7=,DF=AC=×5=,EF=BC=×6=3,
∴△DEF的周长=++3=9,
故选:B.
8.解:连接DN、DB,
在Rt△DAB中,∠A=90°,AB=2,AD=2,
∴BD==4,
∵点E,F分别为DM,MN的中点,
∴EF=DN,
由题意得,当点N与点B重合是DN最大,最大值为4,
∴EF长度的最大值为2,
故选:D.
9.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠EFP=×(180°﹣∠EPF)=×(180°﹣140°)=20°,
故选:D.
10.解:等腰三角形的两条中位线长分别为3和5,
根据三角形中位线定理可知,等腰三角形的两边长为6和10,
当腰为10时,则三边长为10,10,6时,周长为26;
当腰为6时,则三边长为6,6,10时,周长为22,
故选:C.
11.解:过D作DE∥AM交BC的延长线于E.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵DE∥AM,
∴四边形AMED是平行四边形,
∴AD=ME,AM=DE,
∵M是BC的中点,AD=,
∴MB=BC=,
∴BE=BM+ME=13,
∵四边形AMED是平行四边形,
∴AM=DE=5,
∵BD=12,
∴52+122=132,
∴△DBE为直角三角形.
∴BE边上的高为
=,
∴平行四边形ABCD的面积为×=40.
故选:B.
12.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵EF是△ABC的中位线,
∴EF∥BC,BC=2EF,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴ED=EB=3,
∴EF=ED+DF=4,
∴BC=2EF=8,故选:D.
13.解:如图,
以BC为对角线,将AB向上平移3个单位,再向左平移1个单位,B点对应的位置为(﹣2,3)就是第四个顶点D1;
以AB为对角线,将BC向下平移3个单位,再向右平移1个单位,B点对应的位置为(0,﹣3)就是第四个顶点D2′;
以AC为对角线,将AB向上平移3个单位,再向右平移4个单位,C点对应的位置为(7,3)就是第四个顶点D3;
∴第四个顶点D的坐标为:(﹣2,3)或(0,﹣3)或(7,3),
故答案为:(﹣2,3)或(0,﹣3)或(7,3).
14.解:∵?ABCD的周长为36cm,
∴AB+BC=18cm①,
∵过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,
∴4AB=5BC②,
由①②得:AB=10cm,BC=8cm,
∴?ABCD的面积为:AB?DE=40(cm2).
故答案为:40.
15.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故答案为:S1=S2.
16.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD,
又平行四边形ABCD的周长为60cm,△AOB的周长比△BOC的周长长8cm,
∴,
两个方程相加,得AB=19(cm).
故答案为:19.
17.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵AB⊥AC,
∴∠BAC=90°,
∴AC===2,
∴OA=AC=,
∴OB===,
∴BD=2OB=2;
故答案为:2.
18.解:如图,连接CE,过点C作CH⊥AB,交AB的延长线于H,
∵平行四边形ABCD中,∠ABC=135°,AD=4,
∴∠CBH=45°,BC=4,
又∵∠H=90°,
∴∠BCH=45°,
∴CH=BH=4,
设AE=x,则BE=8﹣x,
∵EF垂直平分AC,
∴CE=AE=x,
∵在Rt△CEH中,CH2+EH2=EC2,
∴42+(8﹣x+4)2=x2,
解得x=,
∴AE的长为.
故答案为:.
19.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BAD+∠B=180°,∠DAE=∠AEB,
∴∠BAD=180°﹣∠B=180°﹣52°=128°,
∵AE平分∠BAD,
∴∠AEB=∠DAE=∠BAD=64°,
∴∠AEC=180°﹣∠AEB=180°﹣64°=116°;
故答案为:116°.
20.证明:∵ABCD是平行四边形,
∴AB∥DC,AD=BC,
∴∠ABP=∠BPC,
∵BP平分∠ABC,
∴∠ABP=∠CBP,
∴∠BPC=∠CBP,
∵BC=BP,
∴∠BPC=∠C,
∴∠CBP=∠BPC=∠C,
∴BC=BP=PC,
∴△BPC是等边三角形,
∴∠BPC=∠PBC=∠ABP=∠BAD=60°,
∴四边形DPBA是等腰梯形,
∴∠PAB=∠ABD=43°,
∴∠APB=180°﹣60°﹣43°=77°.
故答案为:77.
21.解:过点A作AE⊥BC于E,过点D作DF⊥BC于F,
设BE=CF=x,AE=DF=y,
则
AC2+BD2=(5﹣x)2+y2+(5+x)2+y2=50+2x2+2y2=50+2×42=82.
故答案为:82.
22.解:如图,延长DC和FE交于点G,
在平行四边形ABCD中,AB∥CD,
∴∠B=∠ECG,
∵E为BC的中点,
∴BE=CE=BC=×4=2,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(ASA),
∴BF=CG,
∵∠B=60°,
∴∠FEB=30°,
∴BF=BE=1,
∴EF=,
∵CG=BF=1,CD=AB=3,
∴DG=CD+CG=3+1=4,
∵EF⊥AB,AB∥CD,
∴DG⊥FG,
∴S△DEF=EF?DG=××4=2.
故答案为:2.
23.解:如图,过点A作AE⊥BC于点E、AF⊥CD于点F.
由题意得,S四边形ABCD=AE×BC=CD×AF,
∵AB=12,BC=26,AE=8,
∴26×8=12×AF,
∴AF=,
即AB与CD间的距离为.
故答案是:.
24.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC=2,AB∥CD,AD∥BC,
∴∠OCD=∠BAC,∠BCO=∠DAC=30°,∠BAD=180°﹣∠ABC=180°﹣105°=75°,
∴∠OCD=∠BAC=75°﹣30°=45°,
分三种情况:
①当点P在BC上,∠POC=90°时,如图1所示:
∵∠BCO=30°,
∴OP=OC=,CP=2OP=;
②当点P在BC上,∠OPC=90°时,如图2所示:
∵∠BCO=30°,
∴OP=OC=1,CP=OP=;
③当点P在CD上,∠OPC=90°时,如图3所示:
∵∠OCD=45°,
∴△OPC是等腰直角三角形,
∴CP=OC=;
综上所述,若△OPC是直角三角形,则CP的长是或或,
故答案为:或或.
25.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)四边形AGCH是菱形.理由如下:
∵△AOE≌△COF,
∴∠EAO=∠FCO,
∴AG∥CH,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形AGCH是平行四边形,
∵AD∥BC,
∴∠HAC=∠ACB,
∵AC平分∠HAG,
∴∠HAC=∠GAC,
∵∠GAC=∠ACB,
∴GA=GC,
∴平行四边形AGCH是菱形.
26.解:在平行四边形ABCD中,AB=CD,
∵BD=CD,
∴BD=BA,
又∵AM⊥BD,DN⊥AB,
∴DN=AM=4,
又∵∠ABD=∠MAP+∠PAB,∠ABD=∠P+∠BAP,
∴∠P=∠PAM,
∴△APM是等腰直角三角形,
∴AP=AM=8.
27.(1)证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABD是等边三角形,F是AB的中点,
∴AD=AB=BD,AB=2AF,DF⊥AB,
∴AF=BC,
在Rt△AFD和Rt△BCA中,
,
∴Rt△AFD≌Rt△BCA(HL),
∴DF=AC,
∵△ACE是等边三角形,
∴∠EAC=60°,AC=AE,
∴∠EAB=∠EAC+∠BAC=90°,
∴DF=AE,
又∵DF⊥AB,
∴DF∥AE,
∴四边形ADFE是平行四边形;
(2)解:由(1)得:△AEF的面积=△ADF的面积=△ABC的面积,AB=BD=4,BC=AB=2,AC=BC=2,
∴四边形BCEF的面积=△ACE的面积+△ABC的面积﹣△AEF的面积=△ACE的面积=×(2)2=3.
28.(1)证明:∵CF∥AB,
∴∠A=∠ECF,
又∵∠AED=∠CEF,DE=FE,
∴△ADE≌△CFE(AAS),
∴AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,且CF∥BD,
∴四边形DBCF是平行四边形;
(2)解:与线段CF相等的所有线段为AD、BD、AE、CE;理由如下:
由(1)得:BD=AD=CF,AE=CE,
∵AB=AC,
∴BD=AD=AE=CE=CF.
29.(1)证明:∵E是AC的中点,
∴AE=CE,
∵CD∥AB,
∴∠AFE=∠CDE,
在△AEF和△CED中,
,
∵∴△AEF≌△CED(AAS),
∴AF=CD,
又∵CD∥AB,即AF∥CD,
∴四边形AFCD是平行四边形;
(2)解:过C作CM⊥AB于M,如图所示:
则∠CMB=∠CMA=90°,
∵CD∥AB,
∴∠B+∠DCB=180°,
∴∠B=180°﹣135°=45°,
∴△BCM是等腰直角三角形,
∴BM=CM,
∵∠BAC=60°,
∴∠ACM=30°,
∴AC=2AM,BM=CM=AM,
∵AM+BM=AB,
∴AM+AM=6,
解得:AM=3﹣3,
∴AC=2AM=6﹣6.
30.(1)证明:∵DE∥AB,EF∥BC,
∴四边形BDEF是平行四边形,
∴EF=BD,
∵点D是BC边的中点,
∴BD=CD,
∴CD=EF;
(2)解:∵BE平分∠ABC,
∴∠FBE=∠DBE,
又∵四边形BDEF是平行四边形,
∴BD=EF,BF=ED,EF∥BD,
∴∠FEB=∠DBE,
∴∠FBE=∠BEF,
∴BF=EF,
∴BD=EF=BF=ED,
又∵BD=CD=6,
∴BD=EF=BF=ED=6,
∴四边形BDEF的周长=6×4=24.
31.(1)证明:∵D,E为AB,AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,
∴DE=CF;
(2)解:由(1)可知,DE∥BC,DE=CF,
∴四边形DCFE为平行四边形,
∴EF=DC,
在等边△ABC中,D为AB中点,
∴CD⊥AB,
∴CD=BC?sin60°=2,
∴EF=2.
32.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=FC,
∵EG=AE,
∴EG=FC;
(2)解:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,AB=CD,S四边形ABCD=4S△ABO,
∵EG=AE,点E为OB的中点,
∴AG、OB互相平分,
∴四边形ABGO是平行四边形,
∴S△ABO=S△BGO,
∴S四边形ABGO=2S△ABO=S四边形ABCD,
∵OA=OC,EG=AE,
∴OE是△ACG的中位线,
∴OE∥CG,
∵四边形ABGO是平行四边形,
∴BG∥AC,
∴四边形BOCG是平行四边形,
∴S四边形BGCO=2S△BGO=2S△ABO=S四边形ABCD,
∵四边形ABGO是平行四边形,
∴GO∥AB,GO=AB,
∵AB∥CD,
∴GO∥CD,GO=CD,
∴四边形CDOG是平行四边形,
∴S四边形CDOG=2S△CDO=2S△ABO=S四边形ABCD,
∵点E,F分别为OB,OD的中点,
∴EF=BD=OD,
∵四边形CDOG是平行四边形,
∴CG∥EF,CG=OD,
∴EF=CG,
∴四边形EFCG是平行四边形,
∴S四边形EFCG=S四边形CDOG=S四边形ABCD,
∴图中的平行四边形ABGO、平行四边形BOCG、平行四边形CDOG、平行四边形EFCG四个平行四边形,每个平行四边形的面积都等于平行四边形ABCD面积的一半.
