2020-2021学年人教版八年级数学下册18.1平行四边形易错题型优生辅导训练(Word版,附答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册18.1平行四边形易错题型优生辅导训练(Word版,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 289.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 00:00:00 | ||
图片预览




文档简介
2020-2021年度人教版八年级数学下册《18.1平行四边形》易错题型优生辅导训练(附答案)
1.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.10
B.12
C.14
D.16
2.?ABCD按如图方式分割成9个小平行四边形,若知道其中n个小平行四边形的周长就能求出?ABCD的周长,那么n的最小值是( )
A.2
B.3
C.4
D.5
3.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种
B.4种
C.5种
D.6种
4.如图,?ABCD的边AB长为4cm,DE平分∠ADC,若∠B=80°,∠DAE=50°,则?ABCD的周长是( )
A.8cm
B.16cm
C.24cm
D.32cm
5.直线a,b,c互相平行,已知a与b的距离为5,b与c的距离为2,则a与c的距离为( )
A.3
B.5
C.7
D.3或7
6.如图所示,AB、CD、EF互相平行,AE、GI、BF互相平行,则图形中有( )个平行四边形.
A.5
B.7
C.8
D.9
7.如图,E是?ABCD的边AD的中点,CE与BA的延长线交于点F,若∠FCD=∠D,则下列结论不成立的是( )
A.AD=CF
B.BF=CF
C.AF=CD
D.DE=EF
8.如图,在?ABCD中,AB=8,AD=6,∠DAB=30°,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( )
A.8
B.4
C.6
D.12
9.如图所示,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,则图中面积相等的平行四边形有( )
A.平行四边形AEPG和平行四边形ABHG
B.平行四边形AEPG和平行四边形PHCF
C.平行四边形ABHG和平行四边形GPFD
D.平行四边形GPFD和平行四边形AEPG
10.下列说法:①平行四边形的任意一条对角线把平行四边形分成两个全等三角形.②平行四边形的面积等于三角形的面积的2倍.③平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形.④平行四边形对角线的交点到一组对边的距离相等,其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
11.已知点A(3,0)、B(﹣1,0)、C(2,3),以A、B、C为顶点画平行四边形,则第四个顶点D的坐标是
.
12.如图,?ABCD,AB=BD=2,AC=4,则AD=
.
13.如图,在四边形ABCD中,∠ADC+∠BCD=220°,E、F分别是AC、BD的中点,P是AB边上的中点,则∠EPF=
°.
14.如图,在?ABCD中,∠D=120°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为
.
15.如图所示,平行四边形ABCD中,对角线AC、BD即交于点O,点E是BC的中点,若平行四边形ABCD的周长为20cm,AC=8cm,则△OEC的周长为
.
16.若一个平行四边形一个内角的平分线把一条边分为2cm和3cm的两条线段,则该平行四边形的周长是
.
17.一个任意三角形的三边长分别是6cm,8
cm,12cm,它的三条中位线把它分成三个平行四边形,则它们中周长最小是
cm.
18.如图,在△ABC中,∠ABC=90°,BC=5.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,且DF=9,则CE的长为
.
19.已知:如图,AD、CE分别是△ABC的角平分线和中线,AD⊥CE,AD=CE=4,则BC的长等于
.
20.如图,点E,F在平行四边形ABCD的对角线BD上,BE=DF,若平行四边形ABCD的面积是20cm2,△ABE的面积是3cm2,则平行四边形AECF的面积是
cm2.
21.如图,在△ABC中,M是BC边的中点,AP平分∠A,BP⊥AP于点P、若AB=12,AC=22,则MP的长为
.
22.?ABCD中,对角线AC、BD相交于点O,且AC⊥AD,∠ADC=45°,过点C作CN⊥BD于点E,交DA延长线于点N,交AB于点F,连接OF,点M为CD的中点,连接EM.
则下列说法正确的是:
①若BC=4,则EM=2;②∠OBC=∠ACN;③∠DCN=∠AFO;
④与△ADO全等的三角形有3个(不包含△ADO);⑤CF+OF=BO.
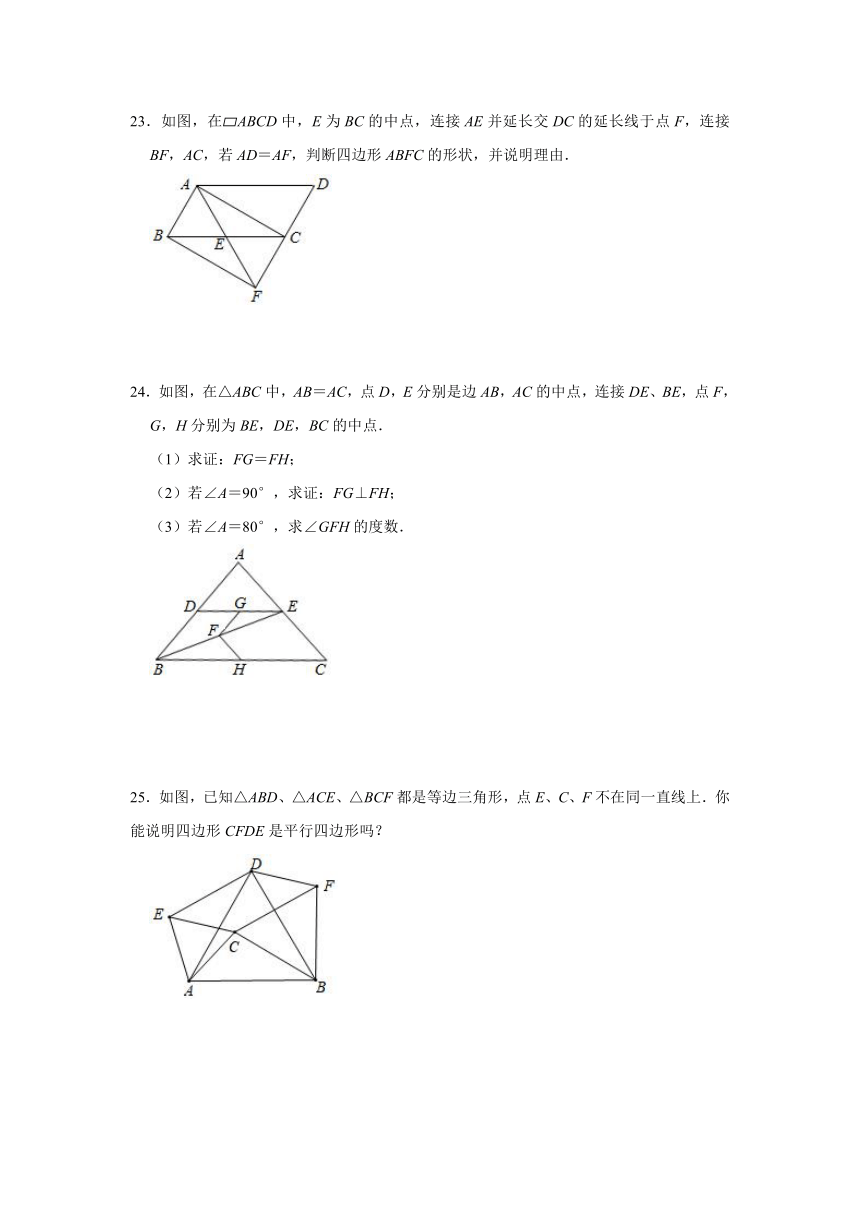
23.如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,判断四边形ABFC的形状,并说明理由.
24.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
25.如图,已知△ABD、△ACE、△BCF都是等边三角形,点E、C、F不在同一直线上.你能说明四边形CFDE是平行四边形吗?
26.如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF.
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
27.(1)如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.求证:FG=(AB+BC+AC).[提示:分别延长AF、AG与直线BC相交]
(2)如图2,若BD、CE分别是△ABC的内角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.
28.如图,?ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
(1)求证:△AOE≌△COF;
(2)证明:四边形AECF是平行四边形.
29.已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G点.
求证:(1)∠AHF=∠BGF;
(2)若AD和BC所在直线互相垂直,求的值.
参考答案
1.解:如图,∵∠AFC=90°,E是AC的中点,
∴Rt△ACF中,EF=AC==5,
∴DE=1+5=6;
∵D,E分别是AB,AC的中点,
∴DE为△ABC的中位线,
∴BC=2DE=12,
故选:B.
2.解:如图,设平行四边形①的周长为a,平行四边形②的周长为b,平行四边形③的周长为c.
由题意易知大平行四边形的周长=a+b+c,
∴知道九个小平行四边形中小平行四边形①②③的周长,就一定能算出这个大平行四边形的周长,
∴n的最小值为3.
故选:B.
3.解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
4.解:∵四边形ABCD是平行四边形,
∴AB=CD=4cm,且AD∥BC,
∴∠ADE=∠CED,
又∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CED=∠CDE,
∴CE=CD=4cm,
∵AD∥BC,
∴∠DAE=∠AEB=50°,
又∵∠B=80°,
∴∠BAE=50°=∠AEB,
∴AB=BE=4cm,
∴BC=8cm,
∴?ABCD的周长=2(4+8)=24(cm),
故选:C.
5.解:分两种情况:
①当直线b在直线a与c之间时,如图.
a与c的距离为5+2=7;
②当直线c在直线a与b之间时,如图.
a与c的距离为5﹣2=3.
故选:D.
6.解:图中有9个平行四边形,有四边形ACHG,四边形ECHI,四边形IHDF,四边形HGBD,四边形ACDB,四边形GIFB,四边形DCEF,四边形AEIG,四边形ABCD,
故选:D.
7.解:∵ABCD是平行四边形,∴AD=BC,∠B=∠D,AB∥CD.
∵BF∥CD,∴∠F=∠FCD,∠FAE=∠D.
∵AE=ED,
∴△AEF≌△DEC.
∴AF=CD,EF=CE.
∵∠FCD=∠D,∴CE=DE.
∴DE=EF.
故C、D都成立;
∵∠B=∠D=∠F,则CF=BC=AD.故A成立.
没有条件证明BF=CF.
故选:B.
8.解:如图,过点D作DG⊥AB于点G,
∵AD=6,∠DAB=30°,∴DG=3,
∴平行四边形ABCD的面积为S=AB?DG=8×3=24,
∴△ABC的面积为S=×24=12
∴△BEF的面积S=×12=4
故选:B.
9.解:A、观察图形,很明显?AEPG的面积小于?ABHG的面积,错误.
B、由于BD、BP、PD分别是?ABCD、?BHPE、?PFDG的对角线,根据“对角线把平行四边形分得的两个三角形全等”,可推出?AEPG和?PHCF面积相等,正确.
C、观察图形,很明显?ABHG和?GPFD的底与高都不相等,错误
D、观察图形,?GPFD和?AEPG高相等,底不相等,面积不相等,错误.
故选:B.
10.解:根据平行四边形的基本性质和判定,可知:
①平行四边形的任意一条对角线把平行四边形分成两个全等三角形,正确.
②平行四边形的面积等于三角形的面积的2倍,说明不清楚,比较对象不明了,所以错误.
③平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形,正确.
④平行四边形对角线的交点到一组对边的距离相等,正确.
故选:C.
11.解:如图,
以BC为对角线,将AB向上平移3个单位,再向左平移1个单位,B点对应的位置为(﹣2,3)就是第四个顶点D1;
以AB为对角线,将BC向下平移3个单位,再向右平移1个单位,B点对应的位置为(0,﹣3)就是第四个顶点D2′;
以AC为对角线,将AB向上平移3个单位,再向右平移4个单位,C点对应的位置为(7,3)就是第四个顶点D3;
∴第四个顶点D的坐标为:(﹣2,3)或(0,﹣3)或(7,3),
故答案为:(﹣2,3)或(0,﹣3)或(7,3).
12.解:如图所示,过A作AE⊥BD于E,
∵AB=2,AO=AC=2,
∴△ABO是等腰三角形,
∴E是BO的中点,
∴BE=OE=BO=BD=,
又∵DO=BD=1,
∴DE=,
∵AE⊥BD,
∴AB2﹣BE2=AD2﹣DE2,
即=AD2﹣,
解得AD=,
故答案为:.
13.解:∵四边形ABCD中,∠ADC+∠BCD=220°,
∴∠BAD+∠ABC=360°﹣220°=140°,
∵E、F分别是AC、BD的中点,P是AB边上的中点,
∴PE是△ABC的中位线,PF是△ABD的中位线,
∴PE∥BC,PF∥AD,
∴∠BPF=∠BAD,∠APE=∠ABC,
∴∠APE+∠BPF=∠BAD+∠ABC=140°,
∴∠EPF=180°﹣140°=40°,
故答案为:40.
14.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=120°,AB∥CD,
∴∠BAD=180°﹣∠D=60°,
∵AE平分∠DAB,
∴∠BAE=60°÷2=30°,
∵AE=AB,
∴∠ABE=(180°﹣30°)÷2=75°,
∴∠EBC=∠ABC﹣∠ABE=45°;
故答案为:45°.
15.解:∵四边形ABCD是平行四边形,其周长为20cm,
∴OA=OC,OB=OD,AB+BC=10cm,
又∵E是BC中点,
∴OE是△ABC的中位线,CE=BC,
∴OE=AB,
∴△OEC的周长=×(AB+BC+AC)=×(10+8)=9(cm),
故答案为:9cm.
16.解:由题意可得,DC=5cm,
∵平行四边形ABCD,
∴∠BAE=∠DEA,
又∵AE为∠DAB的角平分线,
∴∠DAE=∠DEA,
∴△ADE是等腰三角形,AD=DE,
∴当DE=2cm时,该平行四边形的周长是10+4=14cm;
当DE=3cm时,该平行四边形的周长是10+6=16cm.
17.解:如图:AB=6cm,AC=8cm,BC=12cm,D,F,E分别为三角形各边中点.
三条中位线把它分成三个平行四边形,则它们中周长最小的应该是中位线与最短边围成的平行四边形即?ADEF.
AD=EF=3cm,DE=AF=4cm,其周长为2×3+2×4=14(cm)
故答案为14.
18.解:∵BC=5,DE是△ABC的中位线,
∴DE=BC=2.5,DE∥BC,
又∵DF=9,
∴EF=9﹣2.5=6.5,
∵DE∥BC,CF平分∠ACM,
∴∠ECF=∠FCM=∠EFC,
∴CE=FE=6.5,
故答案为:6.5.
19.解:如图,过E作EF∥AD,交BC于F,则∠CEF=90°,
∵E是AB的中点,
∴F是BD的中点,
∴EF是△ABD的中位线,
∴EF=AD=2,
∴Rt△CEF中,CF===2,
∵AD平分∠BAC,AD⊥CE,
∴∠ACE=∠AEC,
∴AC=AE,
∴G是CE的中点,
∵GD∥EF,
∴D是CF的中点,
∴CD=DF=BF=,
∴BC=3,
故答案为:3.
20.解:∵BE=DF,
∴S△ABE=S△ADF=3,
又∵平行四边形ABCD的面积是20cm2,
∴S△ABD=10cm2,
∴S△AEF=4cm2,
∴平行四边形AECF的面积是8cm2,
故答案为:8.
21.解:延长BP与AC相交于D,延长MP与AB相交于E
因为∠BAP=∠DAP,AP⊥BD,AP=AP
所以△ABP≌△APD
于是BP=PD
又∵M是BC边的中点
故PM∥AC
所以∠2=∠3
又因为∠1=∠3
所以∠1=∠2,EP=AE=AB=×12=6
AD=2EP=2×6=12
DC=22﹣12=10
PM=DC=×10=5
故MP的长为5.
故答案为5.
22.解:∵CE⊥DE,M是CD的中点,
∴EM=CD,
又∵AC⊥AD,∠ADC=45°,BC=4=AD,
∴CD=4,
∴EM=2,故①正确;
∵∠DAC=∠CED=90°,∠AOD=∠EOC,
∴∠ADO=∠ACN,
又∵AD∥BC,
∴∠ADO=∠CBO,
∴∠OBC=∠ACN,故②正确;
∵∠DAO=∠CAN=90°,AD=AC,∠ADO=∠ACN,
∴△ADO≌△ACN,
∴AN=AO,
又∵∠FAN=∠ADC=45°=∠BAC,AF=AF,
∴△AFN≌△AFO,
∴∠AFN=∠AFO,
又∵AB∥CD,
∴∠DCN=∠BFC=∠AFN,
∴∠DCN=∠AFO,故③正确;
与△ADO全等的三角形有△ACN和△CBO,有2个,故④错误;
∵△ADO≌△ACN,
∴CN=DO,
即CF+NF=DO,
又∵△AFN≌△AFO,
∴NF=FO,
∴CF+OF=DO=BO,故⑤正确.
综上所述,正确的有①②③⑤.
故答案为:①②③⑤.
23.解:四边形ABFC是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC,
在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS),
∴AB=CF.
∵AB∥CF,
∴四边形ABFC是平行四边形,
∵AD=BC,AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
24.(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点
∴BD=EC
∵点F,G,H分别为BE,DE,BC的中点
∴FG∥BD,GF=
FH∥EC,FH=
∴FG=FH;
(2)证明:由(1)FG∥BD
又∵∠A=90°
∴FG⊥AC
∵FH∥EC
∴FG⊥FH;
(3)解:延长FG交AC于点K,
∵FG∥BD,∠A=80°
∴∠FKC=∠A=80°
∵FH∥EC
∴∠GFH=180°﹣∠FKC=100°
25.证明:∵△ABD、△ACE都是等边三角形,
∴AD=AB,AE=AC,∠BAD=∠CAE=60°,
∴∠BAC=∠DAE,
∴△BAC≌△DAE(SAS),
∴DE=BC,
又∵等边三角形BCF中,CF=BC,
∴DE=CF,
同理可得,DF=EC,
∴四边形DECF是平行四边形.
26.解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠A=∠FDE,∠ABF=∠E,
∵AF=DF,
∴△ABF≌△DEF,
∴AB=DE;
②∵BE平分∠ABC,
∴∠ABF=∠CBF,
∵AD∥BC,
∴∠CBF=∠AFB,
∴∠ABF=∠AFB,
∴AF=AB=3,
∴AD=2AF=6
∵四边形ABCD是平行四边形,
∴BC=AD=6,CD=AB=3,
∵△ABF≌△DEF,
∴DE=AB=3,EF=BF=5,
∴CE=6,BE=EF+BF=10,
∴△BCE的周长=BC+CE+BE=10+6+6=22.
27.解:(1)如图1,∵AF⊥BD,∠ABF=∠MBF,
∴∠BAF=∠BMF,
在△ABF和△MBF中,
,
∴△ABF≌△MBF(ASA),
∴MB=AB,
∴AF=MF,
同理:CN=AC,AG=NG,
∴FG是△AMN的中位线,
∴FG=MN,=(MB+BC+CN),=(AB+BC+AC).
(2)猜想:FG=(AB+AC﹣BC),
证明:如图2,延长AG、AF,与直线BC相交于M、N,
∵由(1)中证明过程类似证△ABF≌△NBF,
∴NB=AB,AF=NF,
同理CM=AC,AG=MG,
∴FG=MN,
∴MN=2FG,
∴BC=BN+CM﹣MN=AB+AC﹣2FG,
∴FG=(AB+AC﹣BC).
28.解:(1)∵四边形ABCD是平行四边形,
∴AO=OC,AB∥CD.
∴∠E=∠F.
∵在△AOE与△COF中,
,
∴△AOE≌△COF(AAS);
(2)如图,连接EC、AF,
由(1)可知△AOE≌△COF,
∴OE=OF,
∵AO=CO,
∴四边形AECF是平行四边形.
29.解:(1)如图所示,连接BD,取BD的中点,连接EP,FP,
∵E、F分别是DC、AB边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
又∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF;
(2)若AD和BC所在直线互相垂直,则PF与PE互相垂直,
∴∠EPF=90°,
又∵PE=PF,
∴△PEF是等腰直角三角形,
∴=,
又∵AD=2PF,
∴,即=.
1.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.10
B.12
C.14
D.16
2.?ABCD按如图方式分割成9个小平行四边形,若知道其中n个小平行四边形的周长就能求出?ABCD的周长,那么n的最小值是( )
A.2
B.3
C.4
D.5
3.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种
B.4种
C.5种
D.6种
4.如图,?ABCD的边AB长为4cm,DE平分∠ADC,若∠B=80°,∠DAE=50°,则?ABCD的周长是( )
A.8cm
B.16cm
C.24cm
D.32cm
5.直线a,b,c互相平行,已知a与b的距离为5,b与c的距离为2,则a与c的距离为( )
A.3
B.5
C.7
D.3或7
6.如图所示,AB、CD、EF互相平行,AE、GI、BF互相平行,则图形中有( )个平行四边形.
A.5
B.7
C.8
D.9
7.如图,E是?ABCD的边AD的中点,CE与BA的延长线交于点F,若∠FCD=∠D,则下列结论不成立的是( )
A.AD=CF
B.BF=CF
C.AF=CD
D.DE=EF
8.如图,在?ABCD中,AB=8,AD=6,∠DAB=30°,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( )
A.8
B.4
C.6
D.12
9.如图所示,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,则图中面积相等的平行四边形有( )
A.平行四边形AEPG和平行四边形ABHG
B.平行四边形AEPG和平行四边形PHCF
C.平行四边形ABHG和平行四边形GPFD
D.平行四边形GPFD和平行四边形AEPG
10.下列说法:①平行四边形的任意一条对角线把平行四边形分成两个全等三角形.②平行四边形的面积等于三角形的面积的2倍.③平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形.④平行四边形对角线的交点到一组对边的距离相等,其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
11.已知点A(3,0)、B(﹣1,0)、C(2,3),以A、B、C为顶点画平行四边形,则第四个顶点D的坐标是
.
12.如图,?ABCD,AB=BD=2,AC=4,则AD=
.
13.如图,在四边形ABCD中,∠ADC+∠BCD=220°,E、F分别是AC、BD的中点,P是AB边上的中点,则∠EPF=
°.
14.如图,在?ABCD中,∠D=120°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为
.
15.如图所示,平行四边形ABCD中,对角线AC、BD即交于点O,点E是BC的中点,若平行四边形ABCD的周长为20cm,AC=8cm,则△OEC的周长为
.
16.若一个平行四边形一个内角的平分线把一条边分为2cm和3cm的两条线段,则该平行四边形的周长是
.
17.一个任意三角形的三边长分别是6cm,8
cm,12cm,它的三条中位线把它分成三个平行四边形,则它们中周长最小是
cm.
18.如图,在△ABC中,∠ABC=90°,BC=5.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,且DF=9,则CE的长为
.
19.已知:如图,AD、CE分别是△ABC的角平分线和中线,AD⊥CE,AD=CE=4,则BC的长等于
.
20.如图,点E,F在平行四边形ABCD的对角线BD上,BE=DF,若平行四边形ABCD的面积是20cm2,△ABE的面积是3cm2,则平行四边形AECF的面积是
cm2.
21.如图,在△ABC中,M是BC边的中点,AP平分∠A,BP⊥AP于点P、若AB=12,AC=22,则MP的长为
.
22.?ABCD中,对角线AC、BD相交于点O,且AC⊥AD,∠ADC=45°,过点C作CN⊥BD于点E,交DA延长线于点N,交AB于点F,连接OF,点M为CD的中点,连接EM.
则下列说法正确的是:
①若BC=4,则EM=2;②∠OBC=∠ACN;③∠DCN=∠AFO;
④与△ADO全等的三角形有3个(不包含△ADO);⑤CF+OF=BO.
23.如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,判断四边形ABFC的形状,并说明理由.
24.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
25.如图,已知△ABD、△ACE、△BCF都是等边三角形,点E、C、F不在同一直线上.你能说明四边形CFDE是平行四边形吗?
26.如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF.
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
27.(1)如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.求证:FG=(AB+BC+AC).[提示:分别延长AF、AG与直线BC相交]
(2)如图2,若BD、CE分别是△ABC的内角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.
28.如图,?ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
(1)求证:△AOE≌△COF;
(2)证明:四边形AECF是平行四边形.
29.已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G点.
求证:(1)∠AHF=∠BGF;
(2)若AD和BC所在直线互相垂直,求的值.
参考答案
1.解:如图,∵∠AFC=90°,E是AC的中点,
∴Rt△ACF中,EF=AC==5,
∴DE=1+5=6;
∵D,E分别是AB,AC的中点,
∴DE为△ABC的中位线,
∴BC=2DE=12,
故选:B.
2.解:如图,设平行四边形①的周长为a,平行四边形②的周长为b,平行四边形③的周长为c.
由题意易知大平行四边形的周长=a+b+c,
∴知道九个小平行四边形中小平行四边形①②③的周长,就一定能算出这个大平行四边形的周长,
∴n的最小值为3.
故选:B.
3.解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
4.解:∵四边形ABCD是平行四边形,
∴AB=CD=4cm,且AD∥BC,
∴∠ADE=∠CED,
又∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CED=∠CDE,
∴CE=CD=4cm,
∵AD∥BC,
∴∠DAE=∠AEB=50°,
又∵∠B=80°,
∴∠BAE=50°=∠AEB,
∴AB=BE=4cm,
∴BC=8cm,
∴?ABCD的周长=2(4+8)=24(cm),
故选:C.
5.解:分两种情况:
①当直线b在直线a与c之间时,如图.
a与c的距离为5+2=7;
②当直线c在直线a与b之间时,如图.
a与c的距离为5﹣2=3.
故选:D.
6.解:图中有9个平行四边形,有四边形ACHG,四边形ECHI,四边形IHDF,四边形HGBD,四边形ACDB,四边形GIFB,四边形DCEF,四边形AEIG,四边形ABCD,
故选:D.
7.解:∵ABCD是平行四边形,∴AD=BC,∠B=∠D,AB∥CD.
∵BF∥CD,∴∠F=∠FCD,∠FAE=∠D.
∵AE=ED,
∴△AEF≌△DEC.
∴AF=CD,EF=CE.
∵∠FCD=∠D,∴CE=DE.
∴DE=EF.
故C、D都成立;
∵∠B=∠D=∠F,则CF=BC=AD.故A成立.
没有条件证明BF=CF.
故选:B.
8.解:如图,过点D作DG⊥AB于点G,
∵AD=6,∠DAB=30°,∴DG=3,
∴平行四边形ABCD的面积为S=AB?DG=8×3=24,
∴△ABC的面积为S=×24=12
∴△BEF的面积S=×12=4
故选:B.
9.解:A、观察图形,很明显?AEPG的面积小于?ABHG的面积,错误.
B、由于BD、BP、PD分别是?ABCD、?BHPE、?PFDG的对角线,根据“对角线把平行四边形分得的两个三角形全等”,可推出?AEPG和?PHCF面积相等,正确.
C、观察图形,很明显?ABHG和?GPFD的底与高都不相等,错误
D、观察图形,?GPFD和?AEPG高相等,底不相等,面积不相等,错误.
故选:B.
10.解:根据平行四边形的基本性质和判定,可知:
①平行四边形的任意一条对角线把平行四边形分成两个全等三角形,正确.
②平行四边形的面积等于三角形的面积的2倍,说明不清楚,比较对象不明了,所以错误.
③平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形,正确.
④平行四边形对角线的交点到一组对边的距离相等,正确.
故选:C.
11.解:如图,
以BC为对角线,将AB向上平移3个单位,再向左平移1个单位,B点对应的位置为(﹣2,3)就是第四个顶点D1;
以AB为对角线,将BC向下平移3个单位,再向右平移1个单位,B点对应的位置为(0,﹣3)就是第四个顶点D2′;
以AC为对角线,将AB向上平移3个单位,再向右平移4个单位,C点对应的位置为(7,3)就是第四个顶点D3;
∴第四个顶点D的坐标为:(﹣2,3)或(0,﹣3)或(7,3),
故答案为:(﹣2,3)或(0,﹣3)或(7,3).
12.解:如图所示,过A作AE⊥BD于E,
∵AB=2,AO=AC=2,
∴△ABO是等腰三角形,
∴E是BO的中点,
∴BE=OE=BO=BD=,
又∵DO=BD=1,
∴DE=,
∵AE⊥BD,
∴AB2﹣BE2=AD2﹣DE2,
即=AD2﹣,
解得AD=,
故答案为:.
13.解:∵四边形ABCD中,∠ADC+∠BCD=220°,
∴∠BAD+∠ABC=360°﹣220°=140°,
∵E、F分别是AC、BD的中点,P是AB边上的中点,
∴PE是△ABC的中位线,PF是△ABD的中位线,
∴PE∥BC,PF∥AD,
∴∠BPF=∠BAD,∠APE=∠ABC,
∴∠APE+∠BPF=∠BAD+∠ABC=140°,
∴∠EPF=180°﹣140°=40°,
故答案为:40.
14.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=120°,AB∥CD,
∴∠BAD=180°﹣∠D=60°,
∵AE平分∠DAB,
∴∠BAE=60°÷2=30°,
∵AE=AB,
∴∠ABE=(180°﹣30°)÷2=75°,
∴∠EBC=∠ABC﹣∠ABE=45°;
故答案为:45°.
15.解:∵四边形ABCD是平行四边形,其周长为20cm,
∴OA=OC,OB=OD,AB+BC=10cm,
又∵E是BC中点,
∴OE是△ABC的中位线,CE=BC,
∴OE=AB,
∴△OEC的周长=×(AB+BC+AC)=×(10+8)=9(cm),
故答案为:9cm.
16.解:由题意可得,DC=5cm,
∵平行四边形ABCD,
∴∠BAE=∠DEA,
又∵AE为∠DAB的角平分线,
∴∠DAE=∠DEA,
∴△ADE是等腰三角形,AD=DE,
∴当DE=2cm时,该平行四边形的周长是10+4=14cm;
当DE=3cm时,该平行四边形的周长是10+6=16cm.
17.解:如图:AB=6cm,AC=8cm,BC=12cm,D,F,E分别为三角形各边中点.
三条中位线把它分成三个平行四边形,则它们中周长最小的应该是中位线与最短边围成的平行四边形即?ADEF.
AD=EF=3cm,DE=AF=4cm,其周长为2×3+2×4=14(cm)
故答案为14.
18.解:∵BC=5,DE是△ABC的中位线,
∴DE=BC=2.5,DE∥BC,
又∵DF=9,
∴EF=9﹣2.5=6.5,
∵DE∥BC,CF平分∠ACM,
∴∠ECF=∠FCM=∠EFC,
∴CE=FE=6.5,
故答案为:6.5.
19.解:如图,过E作EF∥AD,交BC于F,则∠CEF=90°,
∵E是AB的中点,
∴F是BD的中点,
∴EF是△ABD的中位线,
∴EF=AD=2,
∴Rt△CEF中,CF===2,
∵AD平分∠BAC,AD⊥CE,
∴∠ACE=∠AEC,
∴AC=AE,
∴G是CE的中点,
∵GD∥EF,
∴D是CF的中点,
∴CD=DF=BF=,
∴BC=3,
故答案为:3.
20.解:∵BE=DF,
∴S△ABE=S△ADF=3,
又∵平行四边形ABCD的面积是20cm2,
∴S△ABD=10cm2,
∴S△AEF=4cm2,
∴平行四边形AECF的面积是8cm2,
故答案为:8.
21.解:延长BP与AC相交于D,延长MP与AB相交于E
因为∠BAP=∠DAP,AP⊥BD,AP=AP
所以△ABP≌△APD
于是BP=PD
又∵M是BC边的中点
故PM∥AC
所以∠2=∠3
又因为∠1=∠3
所以∠1=∠2,EP=AE=AB=×12=6
AD=2EP=2×6=12
DC=22﹣12=10
PM=DC=×10=5
故MP的长为5.
故答案为5.
22.解:∵CE⊥DE,M是CD的中点,
∴EM=CD,
又∵AC⊥AD,∠ADC=45°,BC=4=AD,
∴CD=4,
∴EM=2,故①正确;
∵∠DAC=∠CED=90°,∠AOD=∠EOC,
∴∠ADO=∠ACN,
又∵AD∥BC,
∴∠ADO=∠CBO,
∴∠OBC=∠ACN,故②正确;
∵∠DAO=∠CAN=90°,AD=AC,∠ADO=∠ACN,
∴△ADO≌△ACN,
∴AN=AO,
又∵∠FAN=∠ADC=45°=∠BAC,AF=AF,
∴△AFN≌△AFO,
∴∠AFN=∠AFO,
又∵AB∥CD,
∴∠DCN=∠BFC=∠AFN,
∴∠DCN=∠AFO,故③正确;
与△ADO全等的三角形有△ACN和△CBO,有2个,故④错误;
∵△ADO≌△ACN,
∴CN=DO,
即CF+NF=DO,
又∵△AFN≌△AFO,
∴NF=FO,
∴CF+OF=DO=BO,故⑤正确.
综上所述,正确的有①②③⑤.
故答案为:①②③⑤.
23.解:四边形ABFC是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC,
在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS),
∴AB=CF.
∵AB∥CF,
∴四边形ABFC是平行四边形,
∵AD=BC,AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
24.(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点
∴BD=EC
∵点F,G,H分别为BE,DE,BC的中点
∴FG∥BD,GF=
FH∥EC,FH=
∴FG=FH;
(2)证明:由(1)FG∥BD
又∵∠A=90°
∴FG⊥AC
∵FH∥EC
∴FG⊥FH;
(3)解:延长FG交AC于点K,
∵FG∥BD,∠A=80°
∴∠FKC=∠A=80°
∵FH∥EC
∴∠GFH=180°﹣∠FKC=100°
25.证明:∵△ABD、△ACE都是等边三角形,
∴AD=AB,AE=AC,∠BAD=∠CAE=60°,
∴∠BAC=∠DAE,
∴△BAC≌△DAE(SAS),
∴DE=BC,
又∵等边三角形BCF中,CF=BC,
∴DE=CF,
同理可得,DF=EC,
∴四边形DECF是平行四边形.
26.解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠A=∠FDE,∠ABF=∠E,
∵AF=DF,
∴△ABF≌△DEF,
∴AB=DE;
②∵BE平分∠ABC,
∴∠ABF=∠CBF,
∵AD∥BC,
∴∠CBF=∠AFB,
∴∠ABF=∠AFB,
∴AF=AB=3,
∴AD=2AF=6
∵四边形ABCD是平行四边形,
∴BC=AD=6,CD=AB=3,
∵△ABF≌△DEF,
∴DE=AB=3,EF=BF=5,
∴CE=6,BE=EF+BF=10,
∴△BCE的周长=BC+CE+BE=10+6+6=22.
27.解:(1)如图1,∵AF⊥BD,∠ABF=∠MBF,
∴∠BAF=∠BMF,
在△ABF和△MBF中,
,
∴△ABF≌△MBF(ASA),
∴MB=AB,
∴AF=MF,
同理:CN=AC,AG=NG,
∴FG是△AMN的中位线,
∴FG=MN,=(MB+BC+CN),=(AB+BC+AC).
(2)猜想:FG=(AB+AC﹣BC),
证明:如图2,延长AG、AF,与直线BC相交于M、N,
∵由(1)中证明过程类似证△ABF≌△NBF,
∴NB=AB,AF=NF,
同理CM=AC,AG=MG,
∴FG=MN,
∴MN=2FG,
∴BC=BN+CM﹣MN=AB+AC﹣2FG,
∴FG=(AB+AC﹣BC).
28.解:(1)∵四边形ABCD是平行四边形,
∴AO=OC,AB∥CD.
∴∠E=∠F.
∵在△AOE与△COF中,
,
∴△AOE≌△COF(AAS);
(2)如图,连接EC、AF,
由(1)可知△AOE≌△COF,
∴OE=OF,
∵AO=CO,
∴四边形AECF是平行四边形.
29.解:(1)如图所示,连接BD,取BD的中点,连接EP,FP,
∵E、F分别是DC、AB边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
又∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF;
(2)若AD和BC所在直线互相垂直,则PF与PE互相垂直,
∴∠EPF=90°,
又∵PE=PF,
∴△PEF是等腰直角三角形,
∴=,
又∵AD=2PF,
∴,即=.
