2020-2021学年八年级数学人教版下册18.2.3.1正方形的性质与判定课件(共17张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册18.2.3.1正方形的性质与判定课件(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 838.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 21:16:47 | ||
图片预览


文档简介
(共17张PPT)
课题:正方形
人教版八年级数学下册第十八章
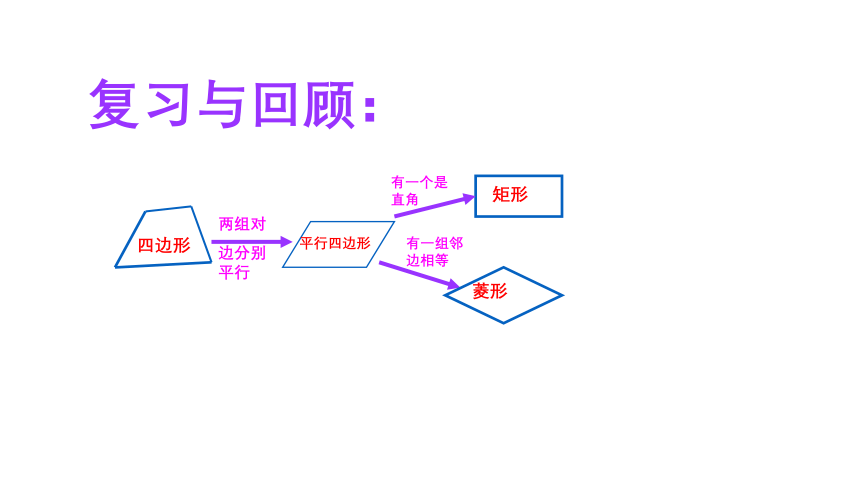
四边形
平行四边形
矩形
菱形
两组对
边分别平行
有一个是直角
有一组邻边相等
复习与回顾:
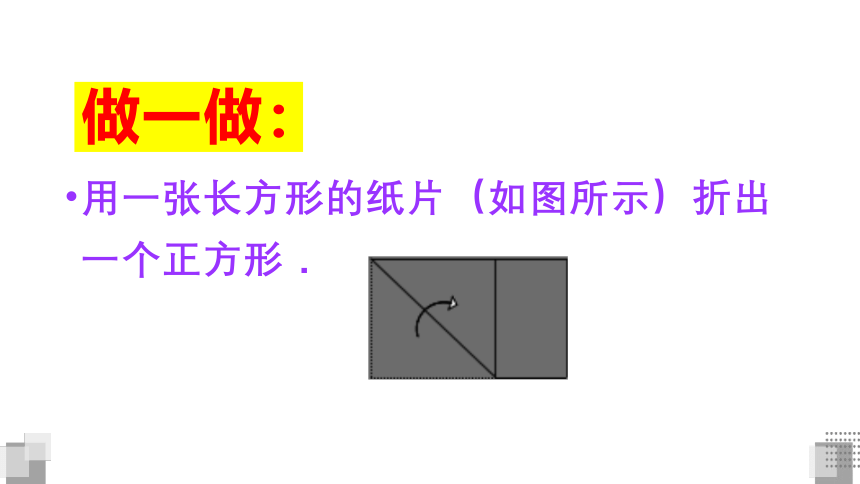
做一做:
用一张长方形的纸片(如图所示)折出一个正方形.
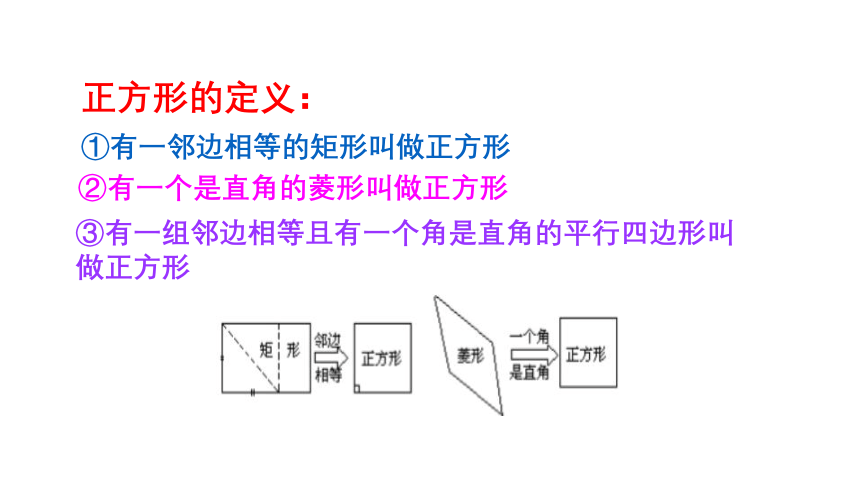
正方形的定义:
①有一邻边相等的矩形叫做正方形
②有一个是直角的菱形叫做正方形
③有一组邻边相等且有一个角是直角的平行四边形叫做正方形
四边形
平行四边形
矩形
菱形
两组对
边分别平行
有一个是直角
有一组邻边相等
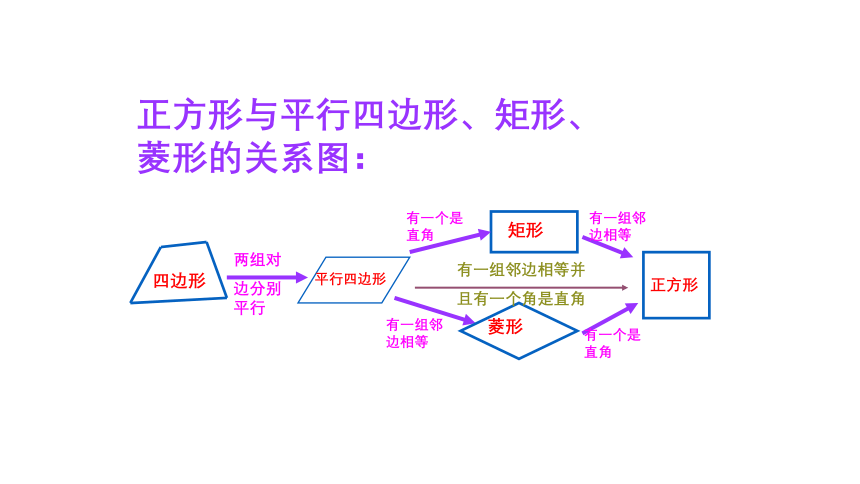
正方形与平行四边形、矩形、菱形的关系图:
正方形
有一个是直角
有一组邻边相等
有一组邻边相等并
且有一个角是直角
正方形的性质:
如图,正方形ABCD
边:
AB∥CD,AD∥BC,AB=BC=CD=AD
角:
∠ABC=∠BCD=∠CDA=∠BAD=90°
对角线:
AC=BD,AO=BO=CO=DO,AC⊥BD
AC平分∠BAD,BD平分∠ABC
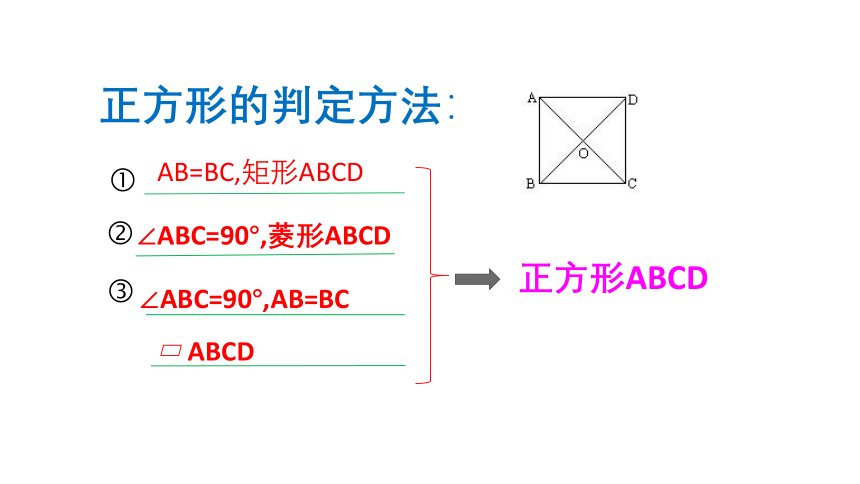
正方形的判定方法:
?
?
?
正方形ABCD
AB=BC,矩形ABCD
∠ABC=90°,菱形ABCD
∠ABC=90°,AB=BC
ABCD
例习题分析:
例1
求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图).
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:
∵
四边形ABCD是正方形,
∴
AC=BD,
AC⊥BD,
AO=CO=BO=DO(正方形的两条对角线相等,并且互相垂直平分).
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
例2
已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.
证明:∵
四边形ABCD是正方形,
∴
∠AOE=∠DOF=90°,AO=DO(正方形的对角线垂直平分且相等).
又
DG⊥AE,
∴
∠EAO+∠AEO=∠EDG+∠AEO=90°.
∴
∠EAO=∠FDO.
∴
△AEO
≌△DFO.
∴
OE=OF.
例3
已知:如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点.
求证:四边形PQMN是正方形.
证明:
∵
PN⊥l1,QM⊥l1,
∴
PN∥QM,∠PNM=90°.
∵
PQ∥NM,
∴
四边形PQMN是矩形.
∵
四边形ABCD是正方形
∴
∠BAD=∠ADC=90°,
AB=AD=DC
∴
∠1+∠2=90°.
又
∠3+∠2=90°,
∴
∠1=∠3.
∴
△ABM≌△DAN.
∴
AM=DN.
同理
AN=DP.
∴
AM+AN=DN+DP
即
MN=PN.
∴
四边形PQMN是正方形(有一组邻边相等的矩形是正方形).
随堂练习:
1.正方形的四条边____
__,四个角___
____,两条对角线____
____.
2.下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形;(
)
②对角线互相垂直的矩形是正方形;(
)
③对角线垂直且相等的四边形是正方形;(
)
④四条边都相等的四边形是正方形;(
)
⑤四个角相等的四边形是正方形.(
)
相等
都是直角
相等且互相垂直平分,每条对角线平分一组对角
√
√
×
×
×
3、已知:如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF.
求证:∠AFE=∠AEF.
A
B
C
D
E
F
随堂练习:
4.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
:
随堂练习
课堂小结:
这节课我们学习了哪些内容?
布置作业:
完成课后练习
课题:正方形
人教版八年级数学下册第十八章
四边形
平行四边形
矩形
菱形
两组对
边分别平行
有一个是直角
有一组邻边相等
复习与回顾:
做一做:
用一张长方形的纸片(如图所示)折出一个正方形.
正方形的定义:
①有一邻边相等的矩形叫做正方形
②有一个是直角的菱形叫做正方形
③有一组邻边相等且有一个角是直角的平行四边形叫做正方形
四边形
平行四边形
矩形
菱形
两组对
边分别平行
有一个是直角
有一组邻边相等
正方形与平行四边形、矩形、菱形的关系图:
正方形
有一个是直角
有一组邻边相等
有一组邻边相等并
且有一个角是直角
正方形的性质:
如图,正方形ABCD
边:
AB∥CD,AD∥BC,AB=BC=CD=AD
角:
∠ABC=∠BCD=∠CDA=∠BAD=90°
对角线:
AC=BD,AO=BO=CO=DO,AC⊥BD
AC平分∠BAD,BD平分∠ABC
正方形的判定方法:
?
?
?
正方形ABCD
AB=BC,矩形ABCD
∠ABC=90°,菱形ABCD
∠ABC=90°,AB=BC
ABCD
例习题分析:
例1
求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图).
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:
∵
四边形ABCD是正方形,
∴
AC=BD,
AC⊥BD,
AO=CO=BO=DO(正方形的两条对角线相等,并且互相垂直平分).
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
例2
已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.
证明:∵
四边形ABCD是正方形,
∴
∠AOE=∠DOF=90°,AO=DO(正方形的对角线垂直平分且相等).
又
DG⊥AE,
∴
∠EAO+∠AEO=∠EDG+∠AEO=90°.
∴
∠EAO=∠FDO.
∴
△AEO
≌△DFO.
∴
OE=OF.
例3
已知:如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点.
求证:四边形PQMN是正方形.
证明:
∵
PN⊥l1,QM⊥l1,
∴
PN∥QM,∠PNM=90°.
∵
PQ∥NM,
∴
四边形PQMN是矩形.
∵
四边形ABCD是正方形
∴
∠BAD=∠ADC=90°,
AB=AD=DC
∴
∠1+∠2=90°.
又
∠3+∠2=90°,
∴
∠1=∠3.
∴
△ABM≌△DAN.
∴
AM=DN.
同理
AN=DP.
∴
AM+AN=DN+DP
即
MN=PN.
∴
四边形PQMN是正方形(有一组邻边相等的矩形是正方形).
随堂练习:
1.正方形的四条边____
__,四个角___
____,两条对角线____
____.
2.下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形;(
)
②对角线互相垂直的矩形是正方形;(
)
③对角线垂直且相等的四边形是正方形;(
)
④四条边都相等的四边形是正方形;(
)
⑤四个角相等的四边形是正方形.(
)
相等
都是直角
相等且互相垂直平分,每条对角线平分一组对角
√
√
×
×
×
3、已知:如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF.
求证:∠AFE=∠AEF.
A
B
C
D
E
F
随堂练习:
4.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
:
随堂练习
课堂小结:
这节课我们学习了哪些内容?
布置作业:
完成课后练习
