七年级数学5.1.2 垂线
图片预览







文档简介
(共34张PPT)
第五章 相交线与平行线
5.1.2 垂线
重庆市开县西街中学 罗堂喜
5.1 相交线
创设情境
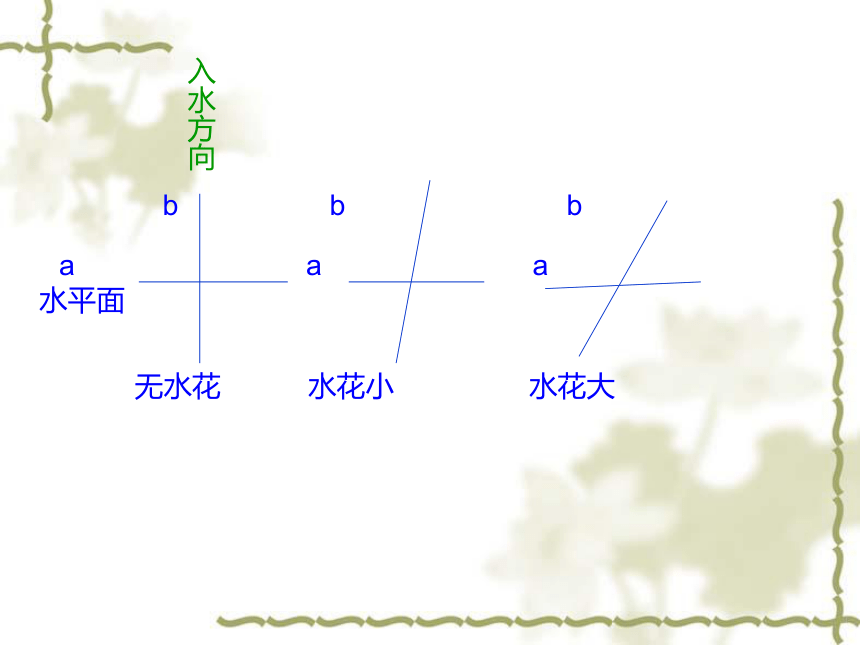
跳水运动员的入水姿势
b b b
a a a
水平面
无水花 水花小 水花大
入水方向
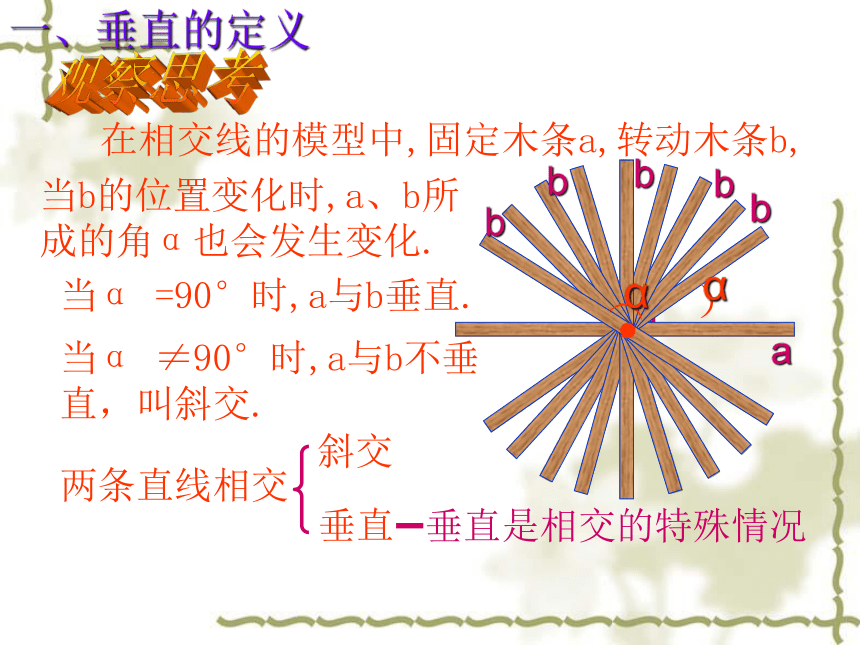
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
一、垂直的定义
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
例如、 如图,a、b互相垂直,O叫垂足,a叫b的垂线,b也叫a的垂线。
b
a
O
1、垂直的定义
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角即可。
α
b
a
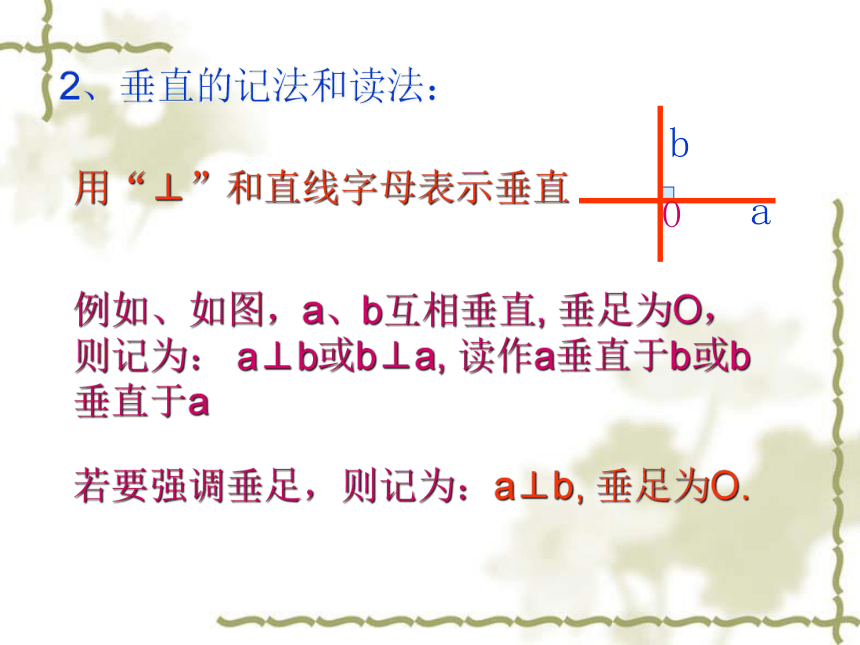
用“⊥”和直线字母表示垂直
O
2、垂直的记法和读法:
例如、如图,a、b互相垂直, 垂足为O,则记为: a⊥b或b⊥a, 读作a垂直于b或b垂直于a
若要强调垂足,则记为:a⊥b, 垂足为O.
A
B
C
D
O
书写形式:
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。
∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)
书写形式:
反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。
3.垂直的书写形式:
∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)
应用垂直的定义:
∠AOC=∠BOC=∠BOD=90°
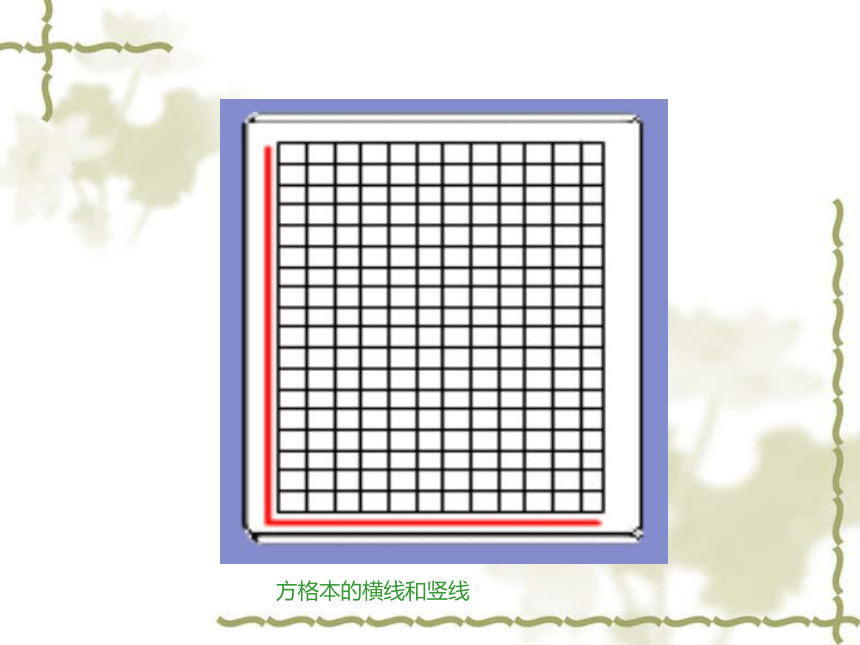
日常生活中,两条直线互相垂直的情形很常见,如下图所示,你能再举出其他例子吗?
二、生活中的垂直
方格本的横线和竖线
铅垂线和水平线
某些标志等
某些建筑物等
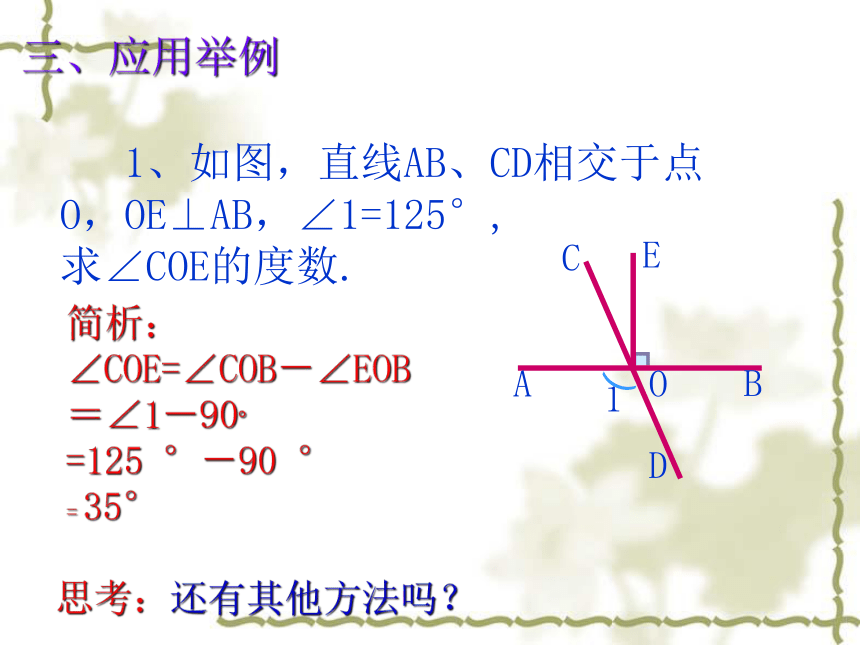
1、如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,
求∠COE的度数.
A
C
E
B
D
O
1
)
简析:
∠COE=∠COB-∠EOB
=∠1-90°
=125 °-90 °
= 35°
思考:还有其他方法吗?
三、应用举例
2.如图,直线AB、CD相交于点O,OE⊥AB,∠1=75°,求∠EOD的度数.
∴ ∠EOB=90°(垂直的定义).
∴ ∠EOD=∠EOB+∠BOD
=90°+75°=165°.
A
C
E
B
D
O
1
(
解:
∵ AB⊥OE (已知),
∵∠BOD=∠1=75°(对顶角相等),
3、如图,∠ABC=90° ,∠1=60° ,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1= ∠2,求∠ABO, ∠BOD.
∵BO⊥AC于O点
1
2
A
B
C
D
O
)
)
(已知)
∵∠ABC=90°( )
∠1=60° ( )
已知
∴∠ABO=30°
解:
(已知)
∴∠BOC=90°
∴∠BOD=30°
(互余的定义)
(互余的定义)
已知
(垂直的定义)
又∵∠2=∠1
∴∠2=60°
(等量代换)
四、垂线的画法
问题:
怎么样画垂线?
一条直线的垂线有无数条.
1、 已知一条直线,你能画出它的垂线吗?能画多少条?
o
1. 放
2. 靠
3. 移
4. 画
过直线上一点有且只有一条直线与已知直线垂直.
2、过直线上一点能画这条直线的垂线吗?能画几条?
o
1. 放
2. 靠
3. 移
4. 画
过直线外一点有且只有一条直线与已知直线垂直.
3、 过直线外一点能画这条直线的垂线吗?能画几条?
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线,即:
垂线的性质1:
过一点有且只有一条直线与已知直线垂直.
E
E
E
4、 如图,请你过点P画出线段AB或射线AB的垂线.
画一条线段或射线的垂线,就是画它们所在直线的垂线.
P
请你画图,把这个问题转化为数学问题.
思考: 在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?
五、垂线段及点到直线的距离
如图PO⊥l ,我们称PO为点P到直线l 的垂线段.
∟
P
0
A
B
C
D
E
F
l
连接直线外一点与直线上各点的所有线段中,垂线段最短.即:
垂线的性质2:
垂线段最短
∟
P
0
A
B
C
D
E
F
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段PO的长度即为点
P 到直线 l 的距离.
点到直线的距离
0
.
注意:距离是个数量.
P
.
∟
l
∟
∟
∟
∟
(1)AB与AC互相垂直;
(2)AD与AC互相垂直;
(3)点C到AB的垂线段是线段AB;
(4)点A到BC的距离是线段AD;
(5)线段AB的长度是点B到AC的距离;
(6)线段AB是点B到AC的距离.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
巩固运用
1.如图,∠BAC = 90°,AD⊥BC,垂足为D,则下列结论:
B
2.下面判断两条直线垂直的方法正确个数是 [ ]
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直.
(2)两条直线相交,有一组邻补角相等,则这两条直线互相垂直.
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直.
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直.
A.4 B.3 C.2 D.1
A
3.两条直线相交所成的四个角中,下列条 件中能判定两条直线垂直的是 [ ]
A.有两个角相等 B.有两对角相等
C.有三个角相等 D.有四对邻补角
4.两个角的平分线相互垂直的有 [ ]
A.两角互补; B.两角互为对顶角;
C.两角都是直角; D.两角为邻补角
C
D
4 .课本P5练习2
中考链接
(2010宁波)如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,∠BOD=45°,则∠COE的度数是( )
B
A.125° B.135° C.145° D.155°
1.若直线m、n相交于点O,
∠1=90°,则__________。
2.若直线AB、CD相交于点O,
且AB⊥CD,那么∠BOD=____。
3.如图,BO⊥AO,∠BOC
与∠BOA的度数之比为1:5,
那么∠COA=_____,
∠BOC的补角为______度。
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162
当堂测试
4.过点P向线段AB所在直线引垂线,正确的是( ).
A B C D
C
当堂测试
5. △ABC中,∠C=90°, △ABC的三条边AB、BC、CA哪条边最长?为什么?
A
B
C
1.垂线的定义;
2.垂线的性质1:经过一点有且只有一条直线与已知直线垂直;
3.垂线的性质2:垂线段最短;
4. 点到直线的距离.
反思总结
方法归纳
2
利用垂直概念和性质可以解决一类求角度的问题。
1.阅读本节课的教材.
2.习题5.1第3、4、5、6、9、10题.
布置作业
第五章 相交线与平行线
5.1.2 垂线
重庆市开县西街中学 罗堂喜
5.1 相交线
创设情境
跳水运动员的入水姿势
b b b
a a a
水平面
无水花 水花小 水花大
入水方向
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
一、垂直的定义
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
例如、 如图,a、b互相垂直,O叫垂足,a叫b的垂线,b也叫a的垂线。
b
a
O
1、垂直的定义
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角即可。
α
b
a
用“⊥”和直线字母表示垂直
O
2、垂直的记法和读法:
例如、如图,a、b互相垂直, 垂足为O,则记为: a⊥b或b⊥a, 读作a垂直于b或b垂直于a
若要强调垂足,则记为:a⊥b, 垂足为O.
A
B
C
D
O
书写形式:
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。
∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)
书写形式:
反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。
3.垂直的书写形式:
∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)
应用垂直的定义:
∠AOC=∠BOC=∠BOD=90°
日常生活中,两条直线互相垂直的情形很常见,如下图所示,你能再举出其他例子吗?
二、生活中的垂直
方格本的横线和竖线
铅垂线和水平线
某些标志等
某些建筑物等
1、如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,
求∠COE的度数.
A
C
E
B
D
O
1
)
简析:
∠COE=∠COB-∠EOB
=∠1-90°
=125 °-90 °
= 35°
思考:还有其他方法吗?
三、应用举例
2.如图,直线AB、CD相交于点O,OE⊥AB,∠1=75°,求∠EOD的度数.
∴ ∠EOB=90°(垂直的定义).
∴ ∠EOD=∠EOB+∠BOD
=90°+75°=165°.
A
C
E
B
D
O
1
(
解:
∵ AB⊥OE (已知),
∵∠BOD=∠1=75°(对顶角相等),
3、如图,∠ABC=90° ,∠1=60° ,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1= ∠2,求∠ABO, ∠BOD.
∵BO⊥AC于O点
1
2
A
B
C
D
O
)
)
(已知)
∵∠ABC=90°( )
∠1=60° ( )
已知
∴∠ABO=30°
解:
(已知)
∴∠BOC=90°
∴∠BOD=30°
(互余的定义)
(互余的定义)
已知
(垂直的定义)
又∵∠2=∠1
∴∠2=60°
(等量代换)
四、垂线的画法
问题:
怎么样画垂线?
一条直线的垂线有无数条.
1、 已知一条直线,你能画出它的垂线吗?能画多少条?
o
1. 放
2. 靠
3. 移
4. 画
过直线上一点有且只有一条直线与已知直线垂直.
2、过直线上一点能画这条直线的垂线吗?能画几条?
o
1. 放
2. 靠
3. 移
4. 画
过直线外一点有且只有一条直线与已知直线垂直.
3、 过直线外一点能画这条直线的垂线吗?能画几条?
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线,即:
垂线的性质1:
过一点有且只有一条直线与已知直线垂直.
E
E
E
4、 如图,请你过点P画出线段AB或射线AB的垂线.
画一条线段或射线的垂线,就是画它们所在直线的垂线.
P
请你画图,把这个问题转化为数学问题.
思考: 在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?
五、垂线段及点到直线的距离
如图PO⊥l ,我们称PO为点P到直线l 的垂线段.
∟
P
0
A
B
C
D
E
F
l
连接直线外一点与直线上各点的所有线段中,垂线段最短.即:
垂线的性质2:
垂线段最短
∟
P
0
A
B
C
D
E
F
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段PO的长度即为点
P 到直线 l 的距离.
点到直线的距离
0
.
注意:距离是个数量.
P
.
∟
l
∟
∟
∟
∟
(1)AB与AC互相垂直;
(2)AD与AC互相垂直;
(3)点C到AB的垂线段是线段AB;
(4)点A到BC的距离是线段AD;
(5)线段AB的长度是点B到AC的距离;
(6)线段AB是点B到AC的距离.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
巩固运用
1.如图,∠BAC = 90°,AD⊥BC,垂足为D,则下列结论:
B
2.下面判断两条直线垂直的方法正确个数是 [ ]
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直.
(2)两条直线相交,有一组邻补角相等,则这两条直线互相垂直.
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直.
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直.
A.4 B.3 C.2 D.1
A
3.两条直线相交所成的四个角中,下列条 件中能判定两条直线垂直的是 [ ]
A.有两个角相等 B.有两对角相等
C.有三个角相等 D.有四对邻补角
4.两个角的平分线相互垂直的有 [ ]
A.两角互补; B.两角互为对顶角;
C.两角都是直角; D.两角为邻补角
C
D
4 .课本P5练习2
中考链接
(2010宁波)如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,∠BOD=45°,则∠COE的度数是( )
B
A.125° B.135° C.145° D.155°
1.若直线m、n相交于点O,
∠1=90°,则__________。
2.若直线AB、CD相交于点O,
且AB⊥CD,那么∠BOD=____。
3.如图,BO⊥AO,∠BOC
与∠BOA的度数之比为1:5,
那么∠COA=_____,
∠BOC的补角为______度。
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162
当堂测试
4.过点P向线段AB所在直线引垂线,正确的是( ).
A B C D
C
当堂测试
5. △ABC中,∠C=90°, △ABC的三条边AB、BC、CA哪条边最长?为什么?
A
B
C
1.垂线的定义;
2.垂线的性质1:经过一点有且只有一条直线与已知直线垂直;
3.垂线的性质2:垂线段最短;
4. 点到直线的距离.
反思总结
方法归纳
2
利用垂直概念和性质可以解决一类求角度的问题。
1.阅读本节课的教材.
2.习题5.1第3、4、5、6、9、10题.
布置作业
