七年级数学5.2.1 平行线
文档属性
| 名称 | 七年级数学5.2.1 平行线 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-15 20:25:19 | ||
图片预览






文档简介
(共27张PPT)
第五章 相交线与平行线
5.2.1 平行线
重庆市开县西街中学 罗堂喜
5.2 平行线及其判定
平行线的定义:
在同一平面内,不相交的两条直线叫做平行线.
平行线有什么特征?
1.在同一平面内
2.不相交
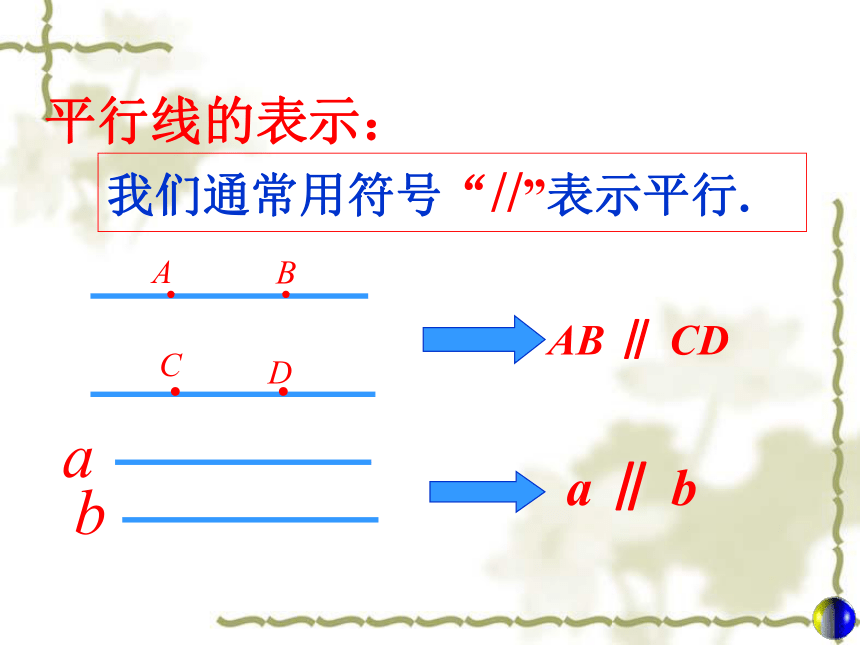
我们通常用符号“//”表示平行.
平行线的表示:
C
D
B
A
·
·
·
·
a ∥ b
AB ∥ CD
a
b
找一找
日常生活中还有哪些实物给我们以平行线的形象?
黑 板
同一平面内的两条直线的位置关系有几种?
相交或平行
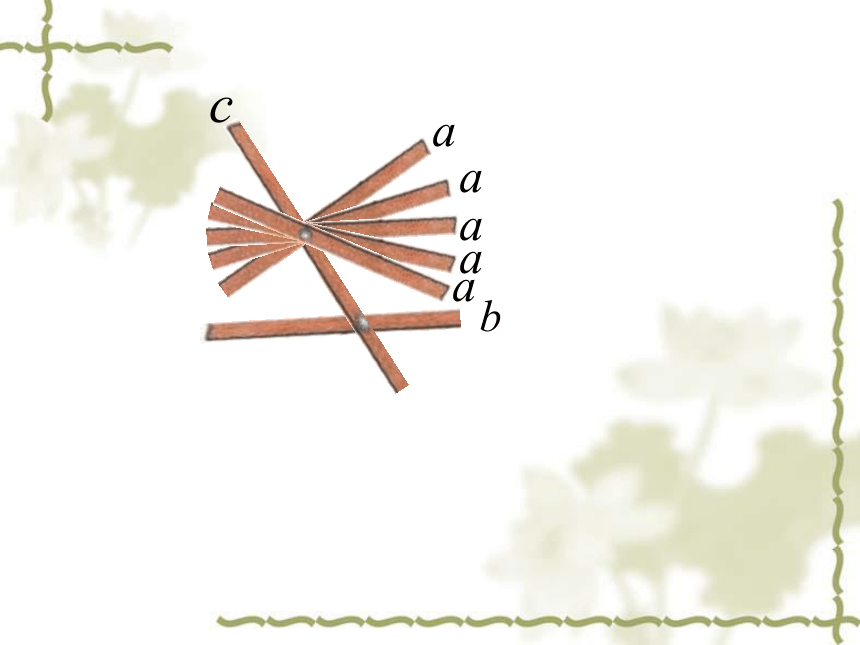
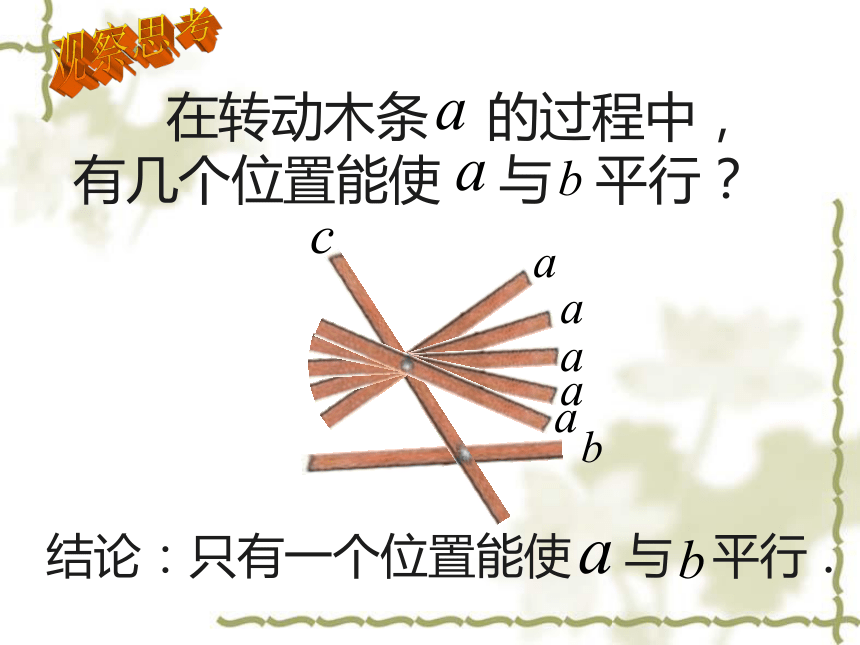
在转动木条 的过程中,有几个位置能使 与 平行?
结论:只有一个位置能使 与 平行 .
一落
二靠
三移
四画
B
C
a
平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
你能过点C画直线 的平行线吗?
a
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
已知直线 和直线 a 外的点B,过点B 画直线 的平行线,怎么画?能画几条?
a
a
应用交流
1.下列说法正确的是( )
A .同一平面内,两条直线的位置关系 只有相交、平行两种
B .同一平面内,不相交的两条线段互相平行
C .不相交的两条直线是平行线
D .同一平面内,不相交的两条射线互相平行
2.在同一平面内,三条直线的交点个数可能是 .
A
0、1、2、3
应用交流
3.读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与直线AB平行;
(2)直线AB,CD是相交直线,点P是直线AB、CD外一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E.
小结归纳
1
1、平行线的概念:在同一平面内,不相交的两条直线叫平行线,记作: a ∥ b。
2、同一平面内,两条直线的位置关系只有平行或相交两种。
3、平行公理:经过直线外一点,有且只有一条直线与已知直线平行。
4、如果两条直线都与第三条直线平行,那么这两条直线也平行。
随堂练习
1、下列说法正确的个数是( )
(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行
A、0 B、1 C、2 D、4
B
2、下列推理正确的是( )
A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。
C
中考链接
1
(2010广西柳州)三条直线a、b、c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定
B
当堂测试
2、
1.
B
经过直线外一点,有且只有一条直线与已知直线平行
0个,1个,2个或3个
4、同一平面内互不重合的三条直线公共点的个数可能是 .
3、判断题
①不相交的两条直线叫做平行线。( )
②在同一平面内,两条不平行的直线必
相交。( )
③在同一平面内不相交的两条线段必平
行。( )
④在同一平面内两条直线的位置只有平
行或相交 。( )
当堂测试
×
×
√
√
5、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
·
·
·
A
D
E
B
C
图 1
A
B
C
D
E
F
图 2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
反思小结
2.在学习的过程中用到了类比的思想方法.
3.要注意总结平行线的画法.
1.本节课主要学行线的定义、表示方法和平行公理及其推论.
布置作业
1.在同一平面内,直线l与两条平行线a、b的位置关系是( )
A.l一定与a、b都平行
B.l可能与a平行,与b相交
C.l一定与a、b都相交
D.l与a、b都平行或都相交
2.在同一平面内,若两条直线没有公共点,则两条直线_________;若有一个公共点,则两条直线___________.
3.习题5.2 第9、11题.
4.选做题:点D是△ABC中AB边上的中点.①过点D作BC的平行线,交AC于E;②量一量AE、CE的长度,它们相等吗?③量一量DE、BC的长度,它们有何关系?
布置作业
活动5:问题探究
问题2:在同一平面内有4条直线,问可以把这个平面分成几部分?
(1)当4条直线两两平行时,可
以把平面分成5部分;
问题2
(2)当4条直线中只有三条两两
平行时,可以把平面分成8部分.
问题2
(3)当4条直线仅有两条互相
平行时,可以把整个平面分成9部分
或10部分 .
问题2
(4)当4条直线中其中两条平行,
另两条也平行时,可以把平面分成9部
分 .
问题2
问题2
(5)当4条直线任意两条都不平
行时,可以把平面分成8或10或11部分;
第五章 相交线与平行线
5.2.1 平行线
重庆市开县西街中学 罗堂喜
5.2 平行线及其判定
平行线的定义:
在同一平面内,不相交的两条直线叫做平行线.
平行线有什么特征?
1.在同一平面内
2.不相交
我们通常用符号“//”表示平行.
平行线的表示:
C
D
B
A
·
·
·
·
a ∥ b
AB ∥ CD
a
b
找一找
日常生活中还有哪些实物给我们以平行线的形象?
黑 板
同一平面内的两条直线的位置关系有几种?
相交或平行
在转动木条 的过程中,有几个位置能使 与 平行?
结论:只有一个位置能使 与 平行 .
一落
二靠
三移
四画
B
C
a
平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
你能过点C画直线 的平行线吗?
a
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
已知直线 和直线 a 外的点B,过点B 画直线 的平行线,怎么画?能画几条?
a
a
应用交流
1.下列说法正确的是( )
A .同一平面内,两条直线的位置关系 只有相交、平行两种
B .同一平面内,不相交的两条线段互相平行
C .不相交的两条直线是平行线
D .同一平面内,不相交的两条射线互相平行
2.在同一平面内,三条直线的交点个数可能是 .
A
0、1、2、3
应用交流
3.读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与直线AB平行;
(2)直线AB,CD是相交直线,点P是直线AB、CD外一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E.
小结归纳
1
1、平行线的概念:在同一平面内,不相交的两条直线叫平行线,记作: a ∥ b。
2、同一平面内,两条直线的位置关系只有平行或相交两种。
3、平行公理:经过直线外一点,有且只有一条直线与已知直线平行。
4、如果两条直线都与第三条直线平行,那么这两条直线也平行。
随堂练习
1、下列说法正确的个数是( )
(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行
A、0 B、1 C、2 D、4
B
2、下列推理正确的是( )
A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。
C
中考链接
1
(2010广西柳州)三条直线a、b、c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定
B
当堂测试
2、
1.
B
经过直线外一点,有且只有一条直线与已知直线平行
0个,1个,2个或3个
4、同一平面内互不重合的三条直线公共点的个数可能是 .
3、判断题
①不相交的两条直线叫做平行线。( )
②在同一平面内,两条不平行的直线必
相交。( )
③在同一平面内不相交的两条线段必平
行。( )
④在同一平面内两条直线的位置只有平
行或相交 。( )
当堂测试
×
×
√
√
5、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
·
·
·
A
D
E
B
C
图 1
A
B
C
D
E
F
图 2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
反思小结
2.在学习的过程中用到了类比的思想方法.
3.要注意总结平行线的画法.
1.本节课主要学行线的定义、表示方法和平行公理及其推论.
布置作业
1.在同一平面内,直线l与两条平行线a、b的位置关系是( )
A.l一定与a、b都平行
B.l可能与a平行,与b相交
C.l一定与a、b都相交
D.l与a、b都平行或都相交
2.在同一平面内,若两条直线没有公共点,则两条直线_________;若有一个公共点,则两条直线___________.
3.习题5.2 第9、11题.
4.选做题:点D是△ABC中AB边上的中点.①过点D作BC的平行线,交AC于E;②量一量AE、CE的长度,它们相等吗?③量一量DE、BC的长度,它们有何关系?
布置作业
活动5:问题探究
问题2:在同一平面内有4条直线,问可以把这个平面分成几部分?
(1)当4条直线两两平行时,可
以把平面分成5部分;
问题2
(2)当4条直线中只有三条两两
平行时,可以把平面分成8部分.
问题2
(3)当4条直线仅有两条互相
平行时,可以把整个平面分成9部分
或10部分 .
问题2
(4)当4条直线中其中两条平行,
另两条也平行时,可以把平面分成9部
分 .
问题2
问题2
(5)当4条直线任意两条都不平
行时,可以把平面分成8或10或11部分;
