七年级数学5.2.2 平行线的判定(2)
文档属性
| 名称 | 七年级数学5.2.2 平行线的判定(2) |  | |
| 格式 | zip | ||
| 文件大小 | 367.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-15 20:28:10 | ||
图片预览



文档简介
(共28张PPT)
第五章 相交线与平行线
5.2.2 平行线的判定(2)
重庆市开县西街中学 罗堂喜
5.2 平行线及其判定
你知道哪些判定两条直线平行的方法?
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.
1.三条直线a、b、c,若a∥b,a∥c,则b_______c,理由是_______________________.
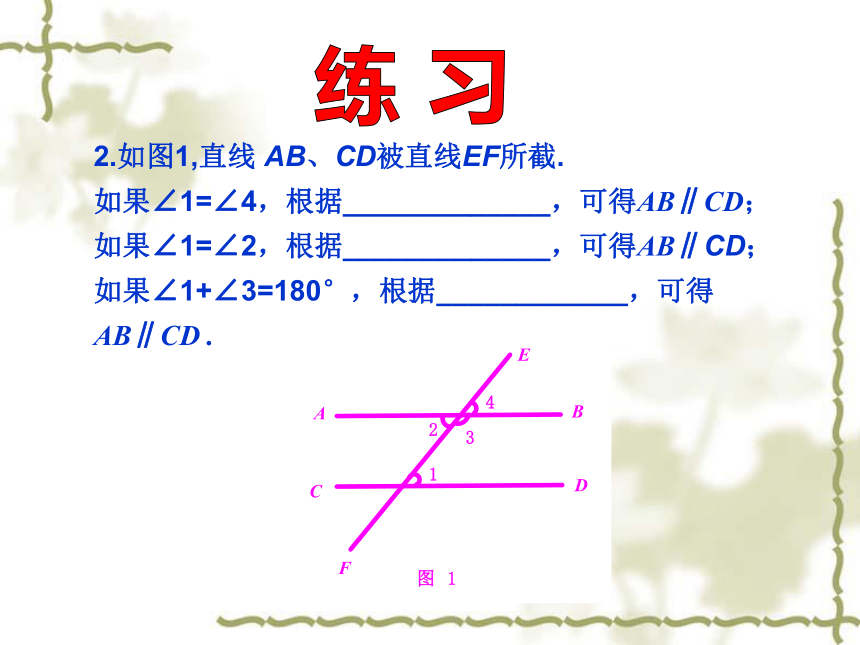
2.如图1,直线 AB、CD被直线EF所截.
如果∠1=∠4,根据_____________,可得AB∥CD;
如果∠1=∠2,根据_____________,可得AB∥CD;
如果∠1+∠3=180°,根据____________,可得AB∥CD .
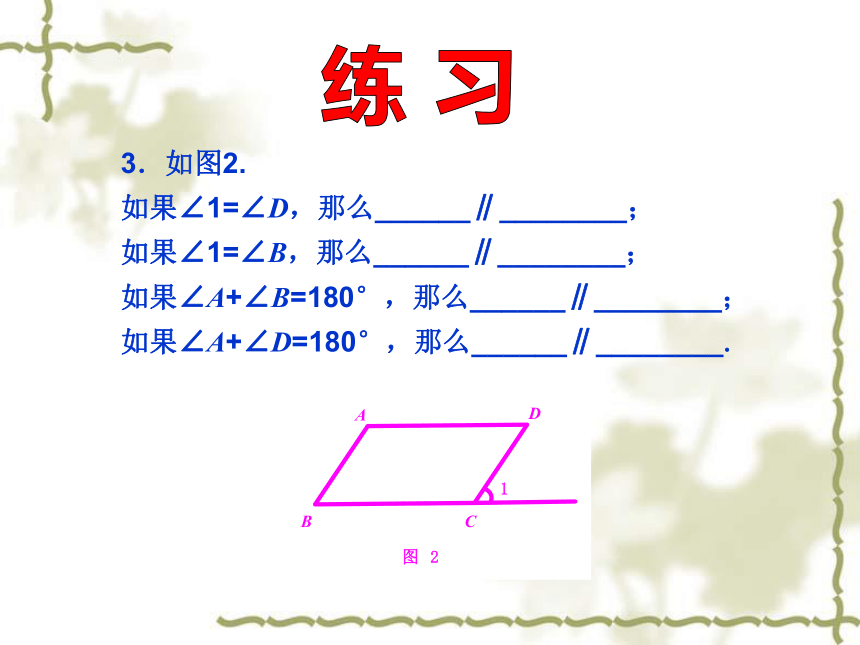
3.如图2.
如果∠1=∠D,那么______∥________;
如果∠1=∠B,那么______∥________;
如果∠A+∠B=180°,那么______∥________;
如果∠A+∠D=180°,那么______∥________.
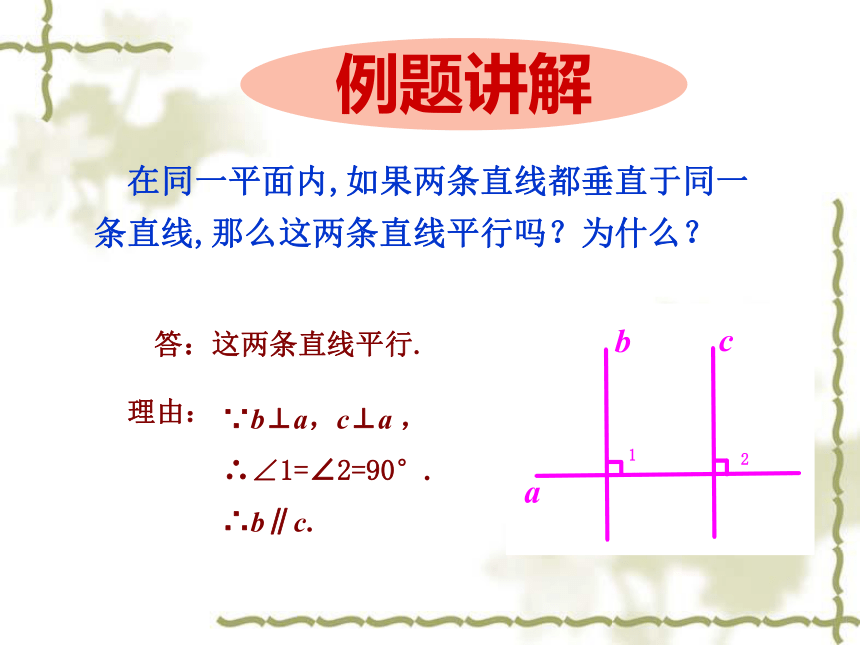
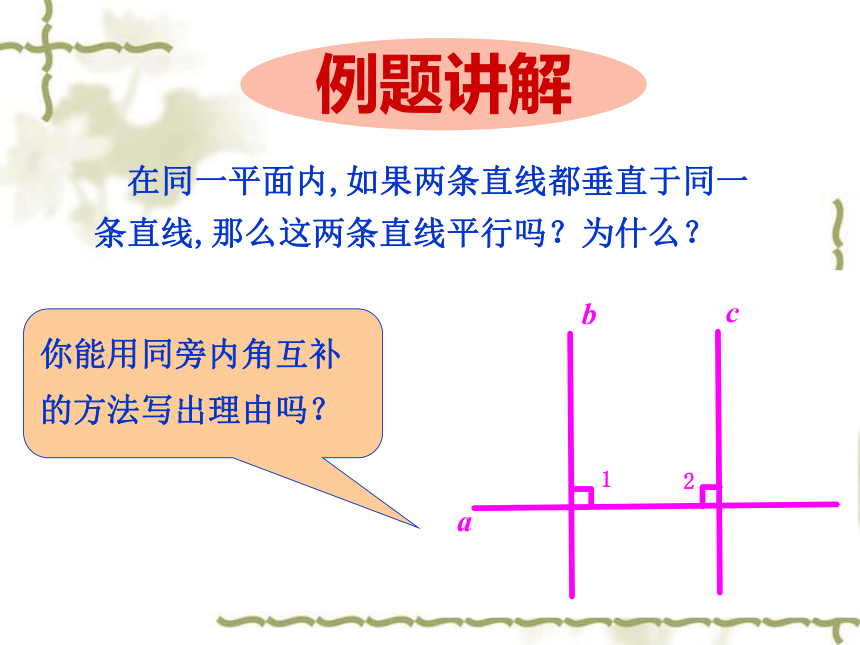
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
答:这两条直线平行.
∵b⊥a,c⊥a ,
∴∠1=∠2=90°.
∴b∥c.
理由:
例题讲解
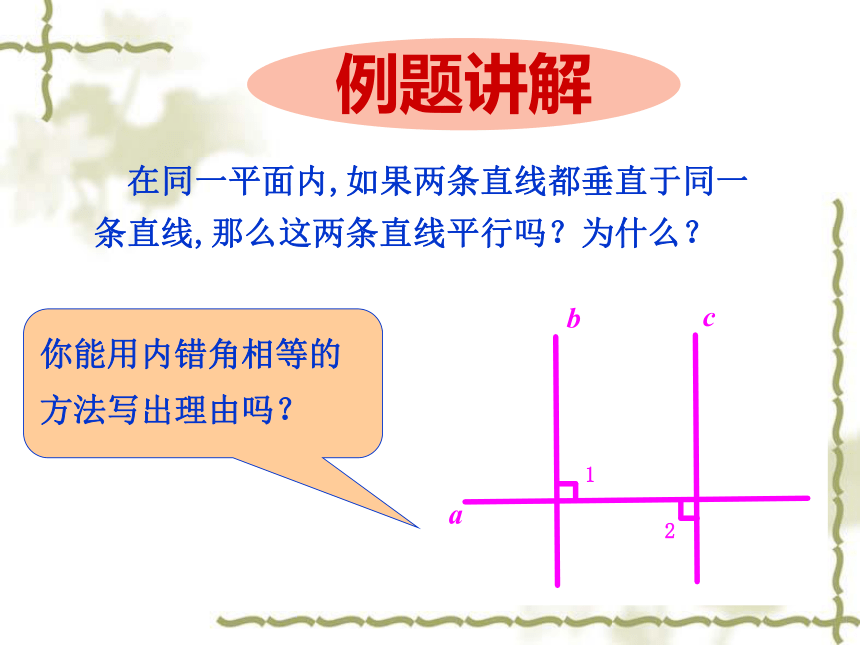
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
你能用内错角相等的方法写出理由吗?
例题讲解
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
你能用同旁内角互补的方法写出理由吗?
例题讲解
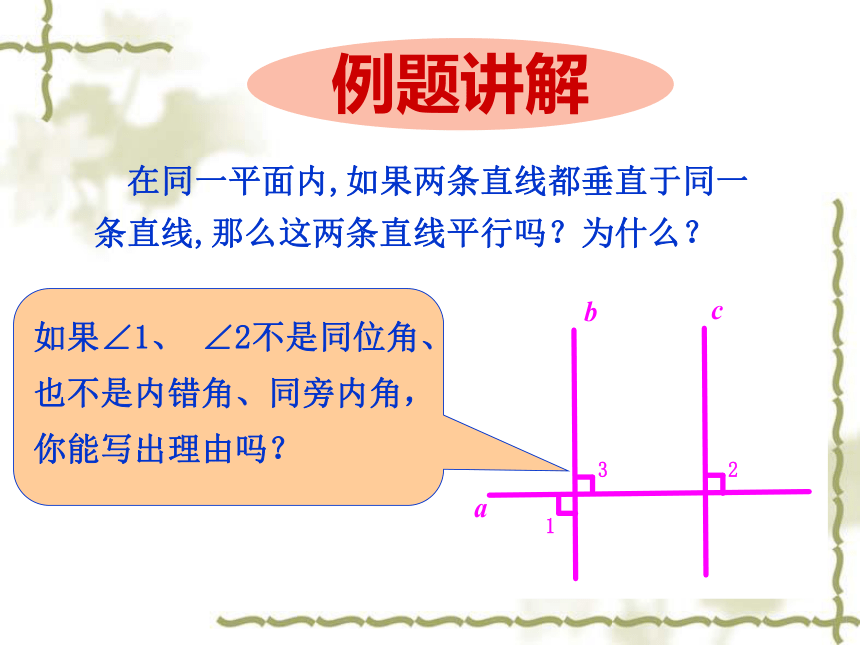
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
如果∠1、 ∠2不是同位角、也不是内错角、同旁内角,你能写出理由吗?
例题讲解
垂直于同一条直线的两条直线平行.
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.平行线的定义.
5.平行公理的推论.
巩固提高
1.这是小明同学自己制作的英语抄写纸的一部分,其中的横格线互相平行吗?你有多少种判别方法?
巩固提高
2.已知:如图,直线a、b被直线c所截,且∠1+∠2=180°,那么直线a与b平行吗 为什么
巩固提高
3. 如图所示,∠1=∠2,∠BAC=20°,∠ACF=80°.
(1)求∠2的度数;
(2)FC与AD平行吗?为什么?
巩固提高
4.如图所示,已知∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
巩固提高
5. 如图所示,如果∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD平行吗?
巩固提高
6.如图所示,已知∠D=∠A,∠B=∠FCB,
试问ED与CF平行吗?
巩固提高
7. 已知,如图,点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?试用两种方法说明理由.
例2、如图,点B在DC上,BE平分∠ABD,∠DBE=∠A,则BE∥AC,请说明理由。
理性提升
A
B
C
D
E
分析:由BE平分∠ABD可以知道什么?联系∠DBE=∠A,又可以知道什么?由此能得出BE∥AC吗?为什么?
解:∵BE平分∠ABD
∴∠ABE=∠DBE(角平分线的定义)
又∠DBE=∠A
∴∠ABE=∠A(等量代换)
∴BE∥AC(内错角相等,两直线平行)
注意:用符号语言书写证明过程时,要步步有据。
1. 如图,∠1=∠2=∠3,填空:
⑴ ∵ ∠1=∠2( )
∴ ∥ . ( )
⑵ ∵∠2=∠3( )
∴ ∥ . ( )
已知
AD
BC
BE
CD
已知
同位角相等,两直线平行
内错角相等,两直线平行
随堂练习
2、如图,在下列条件中可判定哪两条直线平行,并说明根据
(1) ∠1=∠2
(2) ∠3=∠A
(3) ∠A+∠2 + ∠4 =180°
A
B
C
D
1
2
3
4
CD∥AB (内错角相等,两直线平行)
AD∥CB
(同位角相等,两直线平行)
即: ∠A+∠ABC=180 °
AD∥CB
(同旁内角互补,两直线平行)
随堂练习
3、如图,∠1=∠2=55°,试说明直线AB,CD是否平行?
D
A
B
C
E
F
1
2
随堂练习
4、如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗 为什么
(5)∵∠2=∠4(已知)
∴__∥__( )
(2)∵∠1=∠D(已知)
∴__∥__( )
(1)∵∠1=∠B(已知)
∴__∥__( )
(4)∵∠_=∠_(已知)
∴AB∥CD( )
(1)∵∠1=∠B(已知)
∴AD∥BC(同位角相等,两直线平行)
(2)∵∠1=∠D(已知)
∴AB∥CD(内错角相等,两直线平行)
(3)∵∠B+∠BAD=180°(已知)
∴__∥__( )
(3)∵∠B+∠BAD=180°(已知)
∴AD∥BC(同旁内角互补,两直线平行)
(4)∵∠3=∠5(已知)
∴AB∥CD(内错角相等,两直线平行)
(5)∵∠2=∠4(已知)
∴AD∥BC(内错角相等,两直线平行)
1、如图
当堂测试
2、如图,BE平分∠ABC,EC平分∠ BCD, ∠ E=90°
那么AB∥CD吗?为什么?
解:∵BE平分∠ABC(已知)
∴∠___=2∠1
∵EC平分∠BCD(已知)
∴∠____=2∠2
∵∠E+∠1+∠2=180°
∴∠1+∠2=___°-∠E
∵∠E=90°(已知)
∴∠1+∠2=__°
∴∠ABC+∠BCD=2∠_+2∠_=___°
∴_____( )
ABC
BCD
180
90
1 2 180
AB∥CD 同旁内角互补,两直线平行
当堂测试
小结归纳
2
常利用角平分线定义,进行角的等量代换,再结合相关的同位角、内错角或同旁内角等判断平行或进行有关角度的计算。
有时借助三角形内角和为180°解决有关问题。
独立
作业
教材P17面7,P18面12题
走进名校P
2如图:已知∠1=∠2能得出AB∥CD吗?如果能,加以推理;如果不能请再添加一个条件使AB∥CD?
判定两条直线平行的方法
同位角相等,两直线平行.
内错角相等,两直线平行.
如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.
同旁内角互补,两直线平行.
在同一平面内,垂直于
同一直线的两直线平行.
你学会了哪些判定两条直线平行的方法?
布置作业
1.习题5.2 第10、12题.
2.选做题:你能用一张不规则的纸(如图所示的四边形的纸)折出两条平行的直线吗?与同伴说说你的折法.
第五章 相交线与平行线
5.2.2 平行线的判定(2)
重庆市开县西街中学 罗堂喜
5.2 平行线及其判定
你知道哪些判定两条直线平行的方法?
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.
1.三条直线a、b、c,若a∥b,a∥c,则b_______c,理由是_______________________.
2.如图1,直线 AB、CD被直线EF所截.
如果∠1=∠4,根据_____________,可得AB∥CD;
如果∠1=∠2,根据_____________,可得AB∥CD;
如果∠1+∠3=180°,根据____________,可得AB∥CD .
3.如图2.
如果∠1=∠D,那么______∥________;
如果∠1=∠B,那么______∥________;
如果∠A+∠B=180°,那么______∥________;
如果∠A+∠D=180°,那么______∥________.
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
答:这两条直线平行.
∵b⊥a,c⊥a ,
∴∠1=∠2=90°.
∴b∥c.
理由:
例题讲解
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
你能用内错角相等的方法写出理由吗?
例题讲解
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
你能用同旁内角互补的方法写出理由吗?
例题讲解
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
如果∠1、 ∠2不是同位角、也不是内错角、同旁内角,你能写出理由吗?
例题讲解
垂直于同一条直线的两条直线平行.
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.平行线的定义.
5.平行公理的推论.
巩固提高
1.这是小明同学自己制作的英语抄写纸的一部分,其中的横格线互相平行吗?你有多少种判别方法?
巩固提高
2.已知:如图,直线a、b被直线c所截,且∠1+∠2=180°,那么直线a与b平行吗 为什么
巩固提高
3. 如图所示,∠1=∠2,∠BAC=20°,∠ACF=80°.
(1)求∠2的度数;
(2)FC与AD平行吗?为什么?
巩固提高
4.如图所示,已知∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
巩固提高
5. 如图所示,如果∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD平行吗?
巩固提高
6.如图所示,已知∠D=∠A,∠B=∠FCB,
试问ED与CF平行吗?
巩固提高
7. 已知,如图,点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?试用两种方法说明理由.
例2、如图,点B在DC上,BE平分∠ABD,∠DBE=∠A,则BE∥AC,请说明理由。
理性提升
A
B
C
D
E
分析:由BE平分∠ABD可以知道什么?联系∠DBE=∠A,又可以知道什么?由此能得出BE∥AC吗?为什么?
解:∵BE平分∠ABD
∴∠ABE=∠DBE(角平分线的定义)
又∠DBE=∠A
∴∠ABE=∠A(等量代换)
∴BE∥AC(内错角相等,两直线平行)
注意:用符号语言书写证明过程时,要步步有据。
1. 如图,∠1=∠2=∠3,填空:
⑴ ∵ ∠1=∠2( )
∴ ∥ . ( )
⑵ ∵∠2=∠3( )
∴ ∥ . ( )
已知
AD
BC
BE
CD
已知
同位角相等,两直线平行
内错角相等,两直线平行
随堂练习
2、如图,在下列条件中可判定哪两条直线平行,并说明根据
(1) ∠1=∠2
(2) ∠3=∠A
(3) ∠A+∠2 + ∠4 =180°
A
B
C
D
1
2
3
4
CD∥AB (内错角相等,两直线平行)
AD∥CB
(同位角相等,两直线平行)
即: ∠A+∠ABC=180 °
AD∥CB
(同旁内角互补,两直线平行)
随堂练习
3、如图,∠1=∠2=55°,试说明直线AB,CD是否平行?
D
A
B
C
E
F
1
2
随堂练习
4、如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗 为什么
(5)∵∠2=∠4(已知)
∴__∥__( )
(2)∵∠1=∠D(已知)
∴__∥__( )
(1)∵∠1=∠B(已知)
∴__∥__( )
(4)∵∠_=∠_(已知)
∴AB∥CD( )
(1)∵∠1=∠B(已知)
∴AD∥BC(同位角相等,两直线平行)
(2)∵∠1=∠D(已知)
∴AB∥CD(内错角相等,两直线平行)
(3)∵∠B+∠BAD=180°(已知)
∴__∥__( )
(3)∵∠B+∠BAD=180°(已知)
∴AD∥BC(同旁内角互补,两直线平行)
(4)∵∠3=∠5(已知)
∴AB∥CD(内错角相等,两直线平行)
(5)∵∠2=∠4(已知)
∴AD∥BC(内错角相等,两直线平行)
1、如图
当堂测试
2、如图,BE平分∠ABC,EC平分∠ BCD, ∠ E=90°
那么AB∥CD吗?为什么?
解:∵BE平分∠ABC(已知)
∴∠___=2∠1
∵EC平分∠BCD(已知)
∴∠____=2∠2
∵∠E+∠1+∠2=180°
∴∠1+∠2=___°-∠E
∵∠E=90°(已知)
∴∠1+∠2=__°
∴∠ABC+∠BCD=2∠_+2∠_=___°
∴_____( )
ABC
BCD
180
90
1 2 180
AB∥CD 同旁内角互补,两直线平行
当堂测试
小结归纳
2
常利用角平分线定义,进行角的等量代换,再结合相关的同位角、内错角或同旁内角等判断平行或进行有关角度的计算。
有时借助三角形内角和为180°解决有关问题。
独立
作业
教材P17面7,P18面12题
走进名校P
2如图:已知∠1=∠2能得出AB∥CD吗?如果能,加以推理;如果不能请再添加一个条件使AB∥CD?
判定两条直线平行的方法
同位角相等,两直线平行.
内错角相等,两直线平行.
如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.
同旁内角互补,两直线平行.
在同一平面内,垂直于
同一直线的两直线平行.
你学会了哪些判定两条直线平行的方法?
布置作业
1.习题5.2 第10、12题.
2.选做题:你能用一张不规则的纸(如图所示的四边形的纸)折出两条平行的直线吗?与同伴说说你的折法.
