3.3 中心对称一课一练（含解析）

初中数学北师大版八年级下学期 第三章 3.3 中心对称
一、单选题
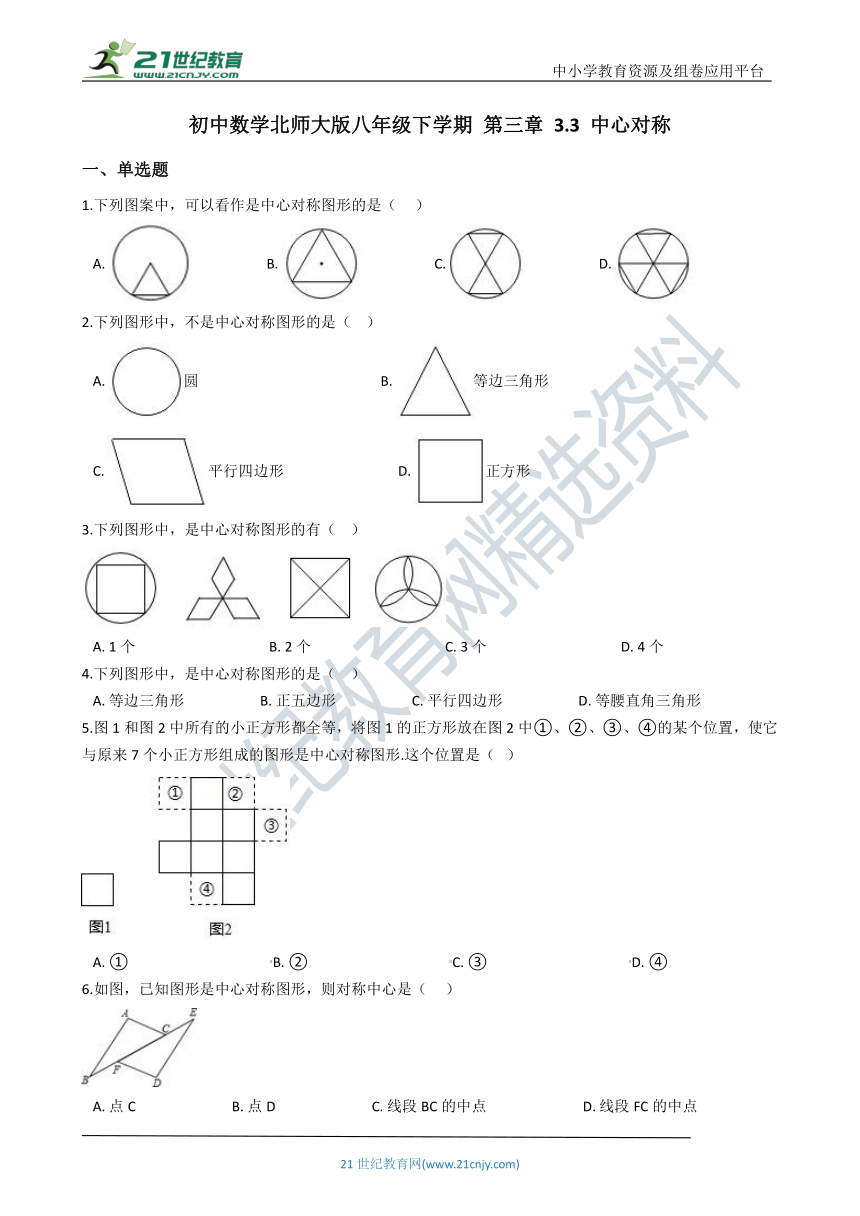
1.下列图案中，可以看作是中心对称图形的是（??? ）
A.??????????????????????B.??????????????????????C.??????????????????????D.?
2.下列图形中，不是中心对称图形的是（?? ）
A.?圆?????????????????????????????????????????????????????B.?等边三角形???
C.?平行四边形?????????????????????????????????D.?正方形
3.下列图形中，是中心对称图形的有（?? ）
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.下列图形中，是中心对称图形的是（?? ）
A.?等边三角形??????????????????????B.?正五边形??????????????????????C.?平行四边形??????????????????????D.?等腰直角三角形
5.图1和图2中所有的小正方形都全等，将图1的正方形放在图2中①、②、③、④的某个位置，使它与原来7个小正方形组成的图形是中心对称图形.这个位置是（? ）
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
6.如图，已知图形是中心对称图形，则对称中心是（??? ）
A.?点C????????????????????????????B.?点D????????????????????????????C.?线段BC的中点????????????????????????????D.?线段FC的中点
7.如图，△ABC和△A1B1C1关于点E成中心对称，则点E坐标是（?? ）
A.?(?3,?1)???????????????????????????????B.?(?3,?3)???????????????????????????????C.?(?3,0)???????????????????????????????D.?(?4,?1)
8.如图所示，已知△ABC与△CDA关于点O对称，过O作EF分别交AD，BC于点E，F，下面的结论：①点E和点F，点B和点D是关于点O的对应点；②直线BD必经过点O；③四边形ABCD是中心对称图形；④四边形DEOC与四边形BFOA的面积必相等；⑤△AOE与△COF成中心对称，其中正确的有（? ）
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?5个
二、填空题
9.如图，如果△ABC和△DEF关于点G成中心对称，那么△ABC绕点G旋转________°后能与△DEF重合.
10.如图， 与 关于点 成中心对称，若 ，则 ________.
11.若点P（﹣2，b）与点M（a，3）关于原点对称，则a+b＝________．
12.已知A,B,O三点不共线，如果点C与点A关于点0对称,点D与点B关于点O对称,那么线段AB与CD的关系是________.
13.矩形是中心对称图形，对矩形ABCD而言，点A的对称点是点________.
14.在平面直角坐标系xOy中，若点B与点A(－2,3) 关于点O中心对称，则点B 的坐标为________.
15.如图,已知 与 成中心对称， 的面积是32,AB=16，则 中,CD边上的高为________.

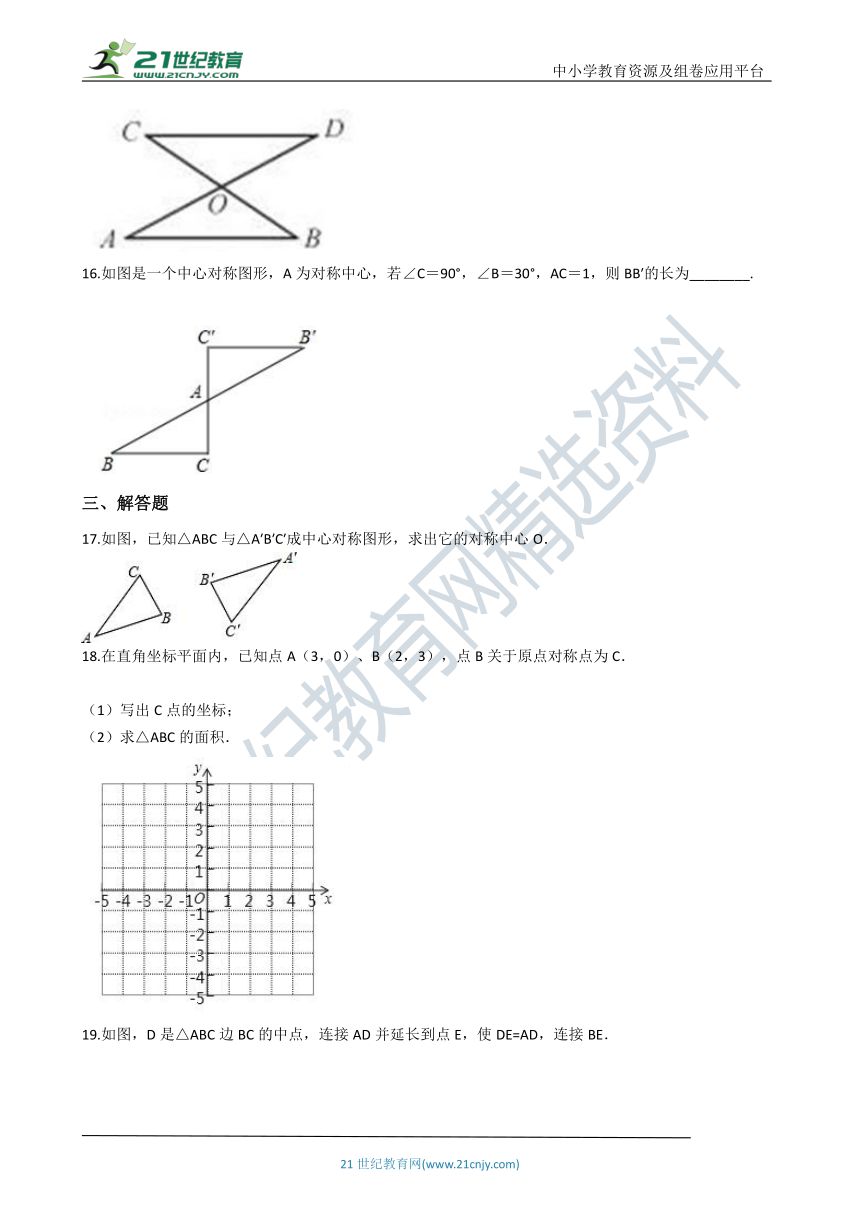
16.如图是一个中心对称图形，A为对称中心，若∠C＝90°，∠B＝30°，AC＝1，则BB′的长为________.
三、解答题
17.如图，已知△ABC与△A′B′C′成中心对称图形，求出它的对称中心O．
18.在直角坐标平面内，已知点A（3，0）、B（2，3），点B关于原点对称点为C．
（1）写出C点的坐标；
（2）求△ABC的面积．
19.如图，D是△ABC边BC的中点，连接AD并延长到点E，使DE=AD，连接BE．
（1）图中哪两个图形成中心对称？
（2）若△ADC的面积为4，求△ABE的面积．
20.如图，在△ABC中，AB=AC，△ABC与△DEC关于点C成中心对称，连接AE、BD．
（1）线段AE、BD具有怎样的位置关系和大小关系？说明你的理由．
（2）如果△ABC的面积为5cm2 ， 求四边形ABDE的面积．
（3）当∠ACB为多少度时，四边形ABDE为矩形？说明你的理由．
21.如图，点P是∠AOB外的一点，点Q与P关于OA对称，点R与P关于OB对称，直线QR分别交OA，OB于点M，N，若PM=PN=3，MN=4，求线段QR的长．

答案解析部分
一、单选题
1.【答案】 C
解：A、不是中心对称图形，故本选项不合题意；
B、不是中心对称图形，故本选项不合题意；
C、是中心对称图形，故本选项符合题意；
D、不是中心对称图形，故本选项不合题意．
故答案为：C．
2.【答案】 B
解：A.是中心对称图形，故本选项不合题意；
B.不是中心对称图形，故本选项符合题意；
C.属于中心对称图形，故本选项不合题意；
D.是中心对称图形，故本选项不合题意；
故答案为：B
3.【答案】 B
解：第一个图形是中心对称图形；
第二个图形不是中心对称图形；
第三个图形是中心对称图形；
第四个图形不是中心对称图形.
故共2个中心对称图形.
故答案为：B.
4.【答案】 C
解：A、不是中心对称图形，故本选项不符合题意；
B、不是中心对称图形，故本选项不符合题意；
C、是中心对称图形，故本选项符合题意；
D、不是中心对称图形，故本选项不符合题意；
故答案为：C.
5.【答案】 C
解：当正方形放在③的位置，即是中心对称图形．
故答案为：C．
6.【答案】 D
解：∵此图形是中心对称图形，
∴对称中心是线段FC的中点．
故答案为：D.
7.【答案】 A
解：连接B1B，C1C,

∵△ABC和△A1B1C1关于点E成中心对称 ，
∴B1B，C1C交于点E,
∴点E（-3，-1）.
故答案为：A.
8.【答案】 D
解：△ABC与△CDA关于点O对称是两个图形的关系，但我们将这两个图形看成一个整体，那么它就是一个以O点为对称中心的中心对称图形，故③正确；
E与F，B与D关于O点对称，图形上的两点的连线若经过对称中心，这两点就是对应点，同时对应点的连线必经过对称中心，所以①②都正确；
四边形DEOC与四边形BFOA是四对对应点所围成的图形，面积必相等，△AOE与△COF也是对应点所围成的图形，所以它们成中心对称，故④和⑤都正确；
故正确的有5个.
故答案为：D.
二、填空题
9.【答案】 180
解：因为△ABC和△DEF关于点G成中心对称，所以△ABC绕点G旋转180°后能与△DEF重合.
故答案为：180.
10.【答案】 2
解： 与△DEC关于点 成中心对称，
.
故答案为：2.
11.【答案】 ﹣1
解：∵点P（﹣2，b）与Q（a，3）关于原点对称，
∴a＝2，b＝﹣3，
∴a+b的值为：2﹣3＝﹣1．
故答案为：﹣1．
12.【答案】 平行且相等
?解：如图，

∵AO=BO，DO=BO，
∴四边形ABCD是平行四边形，
∴AB与CD平行且相等.
故答案为： 平行且相等 .
13.【答案】 C
解：矩形是中心对称图形，对称中心是对角线的交点，点A的对称点是点C，
故答案为：C.
14.【答案】 （2，-3）
解：∵ B与点A(－2,3) 关于点O中心对称，
∴B（2，-3）.
故答案为：（2，-3）.
15.【答案】 16
解：?∵?与??成中心对称，∴△AOB≌△DOC，
∴S△AOB=S△DOC=32，CD=AB=16，
∴CD边上的高为32×2÷16=4.
故答案为：16.
16.【答案】 4
解：∵△ABC与△AB'C'关于点A对称，
∴AB=AB'，
∵∠C=90°，∠B=30°，
∴AB=2AC=2，
∴AB‘=2AB=2×2=4.
故答案为：4.
三、解答题
17.【答案】 解：连接BB′，找BB′中点O或者连接BB′、CC′，交点为对称中心O．
如图所示：
18.【答案】 解：（1）B（2，3）关于原点对称点为C（﹣2，﹣3）；
（2）∵S△AOB= =，
S△AOC==，
∴S△ABC=S△AOB+S△AOC=9．
19.【答案】 （1）解：图中△ADC和三角形EDB成中心对称。
（2）解：∵△ADC和三角形EDB成中心对称，△ADC的面积为4，
∴△EDB的面积也为4，
∵D为BC的中点，
∴△ABD的面积也为4，
所以△ABE的面积为8。
20.【答案】 解：（1）∵△ABC与△DEC关于点C成中心对称，
∴AC=CD，BC=CE，
∴四边形ABDE是平行四边形，
∴AE与BD平行且相等；
（2）∵四边形ABDE是平行四边形，
∴S△ABC=S△BCD=S△CDE=S△ACE ，
∵△ABC的面积为5cm2 ，
∴四边形ABDE的面积=4×5=20cm2；
（3）∠ACB=60°时，四边形ABDE为矩形．
理由如下：∵AB=AC，∠ACB=60°，
∴△ABC是等边三角形，
∴AC=BC，
∵四边形ABDE是平行四边形，
∴AD=2AC，BE=2BC，
∴AD=BE，
∴四边形ABDE为矩形．
21.【答案】 解：∵点P与Q关于OA对称，
∴OA垂直平分PQ，
∴PM=MQ=3．
同理可得：PN=NR=3．
∵MN=4，
∴MQ+QN=4，
∴QN=4﹣MQ=4﹣3=1，
∴QR=QN+NR=1+3=4．