3.1 图形的平移一课一练（含解析）

初中数学北师大版八年级下学期 第三章 3.1 图形的平移
一、单选题
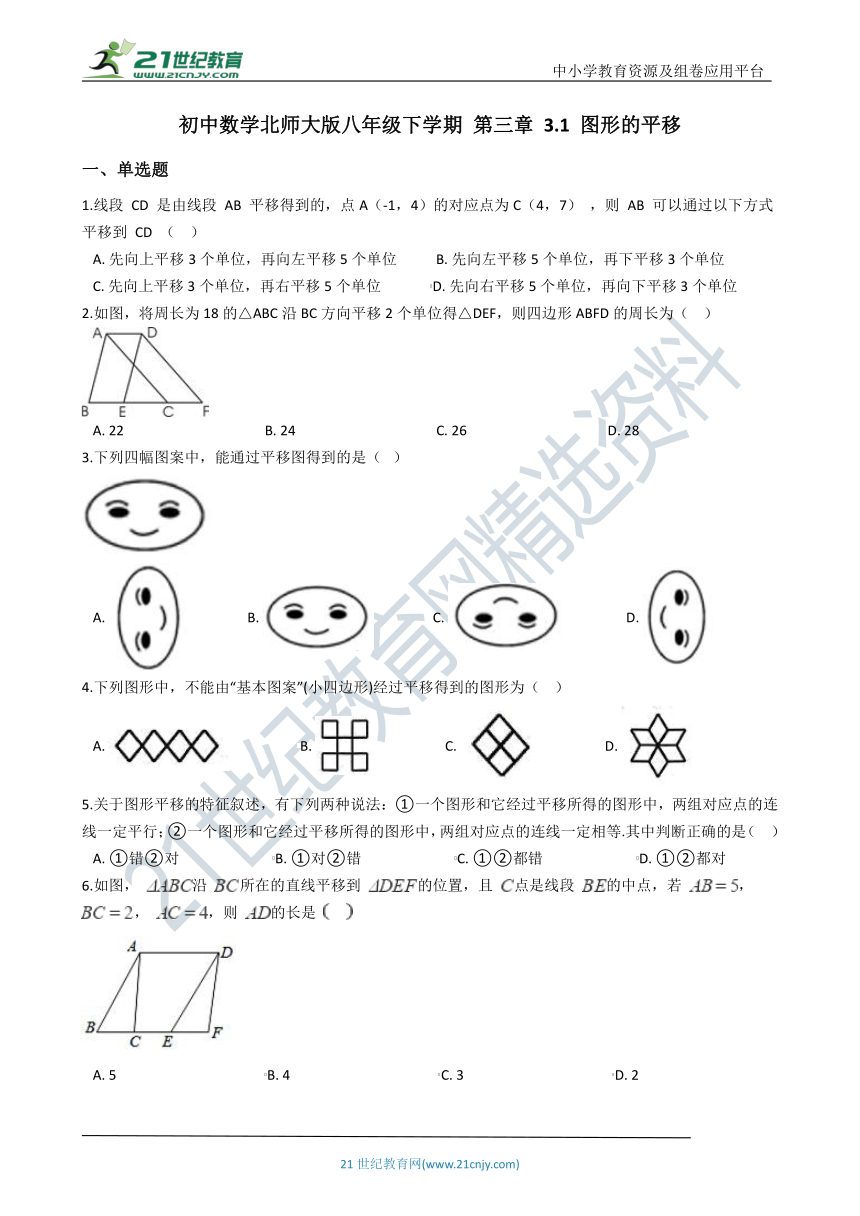
1.线段 CD 是由线段 AB 平移得到的，点A（-1，4）的对应点为C（4，7） ，则 AB 可以通过以下方式平移到 CD （?? ）
A.?先向上平移3个单位，再向左平移5个单位???????????B.?先向左平移5个单位，再下平移3个单位
C.?先向上平移3个单位，再右平移5个单位??????????????D.?先向右平移5个单位，再向下平移3个单位
2.如图，将周长为18的△ABC沿BC方向平移2个单位得△DEF，则四边形ABFD的周长为（?? ）
A.?22?????????????????????????????????????????B.?24?????????????????????????????????????????C.?26?????????????????????????????????????????D.?28
3.下列四幅图案中，能通过平移图得到的是（? ）
A.??????????????????B.??????????????????C.??????????????????D.?
4.下列图形中，不能由“基本图案”(小四边形)经过平移得到的图形为（?? ）
A.?????????????????????B.?????????????????????C.?????????????????????D.?
5.关于图形平移的特征叙述，有下列两种说法：①一个图形和它经过平移所得的图形中，两组对应点的连线一定平行；②一个图形和它经过平移所得的图形中，两组对应点的连线一定相等.其中判断正确的是（?? ）
A.?①错②对???????????????????????????B.?①对②错???????????????????????????C.?①②都错???????????????????????????D.?①②都对
6.如图， 沿 所在的直线平移到 的位置，且 点是线段 的中点，若 ， ， ，则 的长是 ???
A.?5???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
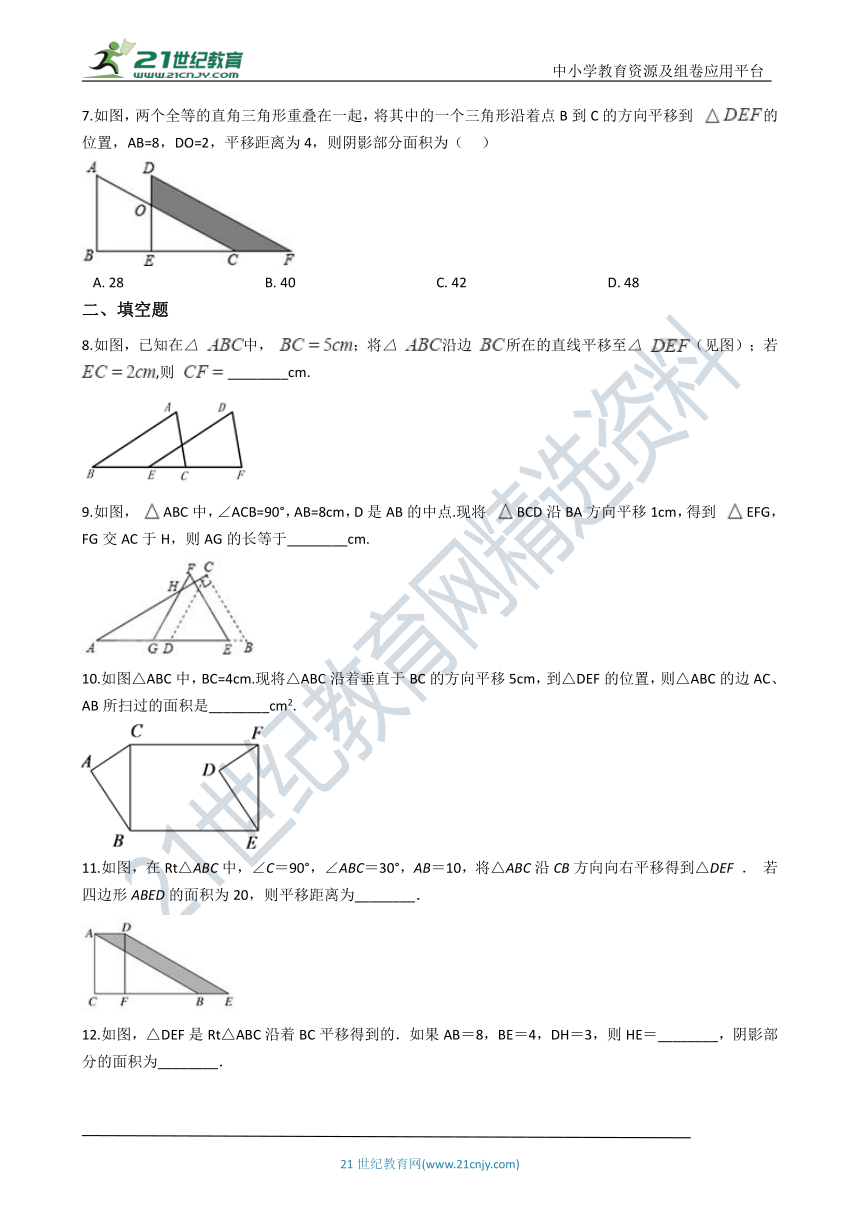
7.如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到 的位置，AB=8，DO=2，平移距离为4，则阴影部分面积为（??? ）
A.?28?????????????????????????????????????????B.?40?????????????????????????????????????????C.?42?????????????????????????????????????????D.?48
二、填空题
8.如图，已知在△ 中， ；将△ 沿边 所在的直线平移至△ （见图）；若 ,则 ________cm.
9.如图， ABC中，∠ACB=90°，AB=8cm，D是AB的中点.现将 BCD沿BA方向平移1cm，得到 EFG，FG交AC于H，则AG的长等于________cm.
10.如图△ABC中，BC=4cm.现将△ABC沿着垂直于BC的方向平移5cm，到△DEF的位置，则△ABC的边AC、AB所扫过的面积是________cm2.
11.如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，AB＝10，将△ABC沿CB方向向右平移得到△DEF ． 若四边形ABED的面积为20，则平移距离为________．
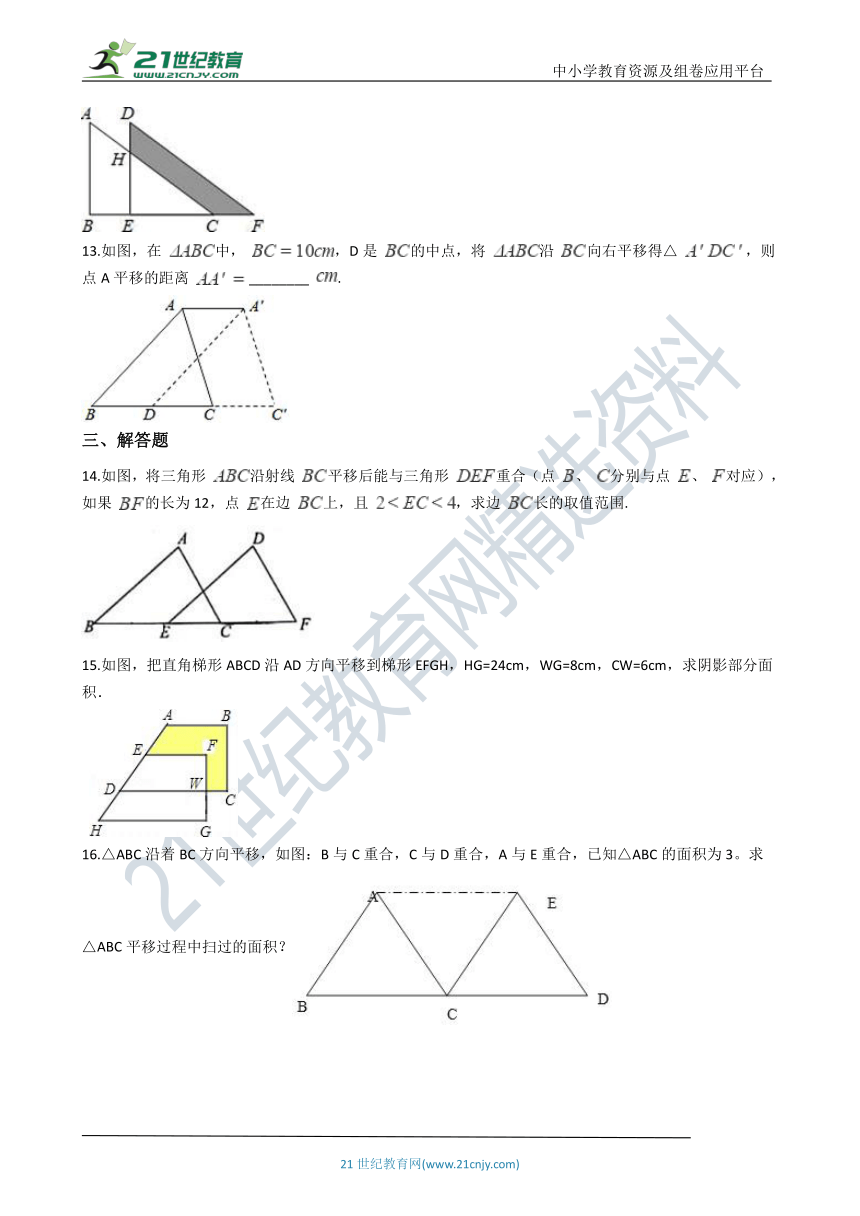
12.如图，△DEF是Rt△ABC沿着BC平移得到的．如果AB＝8，BE＝4，DH＝3，则HE＝________，阴影部分的面积为________．
13.如图，在 中， ，D是 的中点，将 沿 向右平移得△ ，则点A平移的距离 ________ .
三、解答题
14.如图，将三角形 沿射线 平移后能与三角形 重合（点 、 分别与点 、 对应），如果 的长为12，点 在边 上，且 ，求边 长的取值范围.
15.如图，把直角梯形ABCD沿AD方向平移到梯形EFGH，HG=24cm，WG=8cm，CW=6cm，求阴影部分面积．

16.△ABC沿着BC方向平移，如图：B与C重合，C与D重合，A与E重合，已知△ABC的面积为3。求△ABC平移过程中扫过的面积？
17.如图所示，点A、B、C分别平移到了点D、E、F，请你指出图中有哪些相等的线段和相等的角？
答案解析部分
一、单选题
1.【答案】 C
解：∵ 对应
∴横坐标-1+5=4，纵坐标4+3=7，
根据平移的性质可得：先向上平移3个单位，再右平移5个单位
故答案为：C.
2.【答案】 A
解：∵△ABC沿BC方向平移2个单位得到△DEF，
∴AD=CF=2，AC=DF，
∴四边形ABFD的周长=AB+（BC+CF）+DF+AD=AB+BC+AC+AD+CF，
∵△ABC的周长=18，
∴AB+BC+AC=18，
∴四边形ABFD的周长=18+2+2=22.
故答案为：A.
3.【答案】 B
解：平移：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移；
观察四个选项可知，只有选项B能通过平移图得到，
故答案为：B.
4.【答案】 D
解：观察图象可知，选项A，B，C都是可以由基本图形平移得到，
选项D是旋转变换图形，不符合题意，
故答案为：D.
5.【答案】 A
解：一个图形和它经过平移所得的图形中，两组对应点的连线平行或共线；所以①的说法错误；
一个图形和它经过平移所得的图形中，两组对应点的连线一定相等，所以②的说法正确.
故答案为：A.
6.【答案】 B
解：由平移的性质可知， ，
， ，
，
，
故答案为：B.
7.【答案】 A
解：∵△ABC沿着点B到C的方向平移到△DEF的位置，平移距离为4，
∴S△ABC=S△DEF ， BE=4，DE=AB=8，
∴OE=DE-DO=6，
∵S阴影部分+S△OEC=S梯形ABEO+S△OEC ，
∴S阴影部分=S梯形ABEO= ×（6+8）×4=28．
故答案为：A．
二、填空题
8.【答案】 3
解：∵将△ABC沿边BC所在的直线平移至△DEF，
∴BE=CF=BC?EC=5?2=3cm，
故答案为3.
9.【答案】 3
解：∵ D为AB的中点，AB=8cm，
∴AD=BD=4cm，
∵将 BCD沿BA方向平移1cm，得到 EFG，
∴DG=1cm，
∴AG=AD-GD=3cm，
故答案为：3.
10.【答案】 20
解：连接AD，

依题意可得△ABC的边AC、AB所扫过的面积是4×5=20 cm2.
故答案为：20.
11.【答案】 4
解：在Rt△ABC中，∵∠ABC=30°，
∴AC= AB=5，
∵△ABC沿CB向右平移得到△DEF，
∴AD=BE，AD BE，
∴四边形ABED为平行四边形，
∵四边形ABED的面积等于20，
∴AC?BE=20，即5BE=20，
∴BE=4，即平移距离等于4．
故答案为：4．
12.【答案】 5；26
解：∵Rt△ABC沿BC方向平移得到Rt△DEF，
∴AB=DE=8，△ABC≌△DEF，
∴阴影部分面积=梯形ABEH的面积，
∵DH=3，
∴EH=8-3=5，
∴阴影部分面积= ×（5+8）×4=26．
故答案为5，26．
13.【答案】 5
解：观察图象可知平移的距离 ，
故答案为5.
三、解答题
14.【答案】 解：由题意可知BC=EF，则由图可知BC+EF-EC=BF，
则2BC=BF+EC，即BC= ?(BF+EC)，
由 的长为12，且 可得：
.
15.【答案】 解：由平移的性质，梯形ABCD的面积=梯形EFGH的面积，CD=HG=24cm，
∴阴影部分的面积=梯形DWGH的面积，
∵CW=6cm，
∴DW=CD﹣CW=24﹣6=18cm，
∴阴影部分的面积= （DW+HG）?WG= （18+24）×8=168cm2 ．
答：阴影部分面积是168cm2 ．
【答案】
解：∵AE∥CD? AC∥DE?∴△ACE和 △ECD和△ABC等底等高，所以S△ACE+S△ECD=2S△ABC=2×3=6．
17.【答案】相等的线段有：AB＝DE，BC＝EF，AC＝DF，AD＝BE＝CF；相等的角有：∠BAC＝∠EDF，∠ABC＝∠DEF，∠ACB＝∠DFE．
由平移的性质得：相等的线段有：AB＝DE，BC＝EF，AC＝DF，AD＝BE＝CF；相等的角有：∠BAC＝∠EDF，∠ABC＝∠DEF，∠ACB＝∠DFE．