2020-2-21学年北师版七下数学单元练习附答案第三章变量之间的关系(word版含答案)
文档属性
| 名称 | 2020-2-21学年北师版七下数学单元练习附答案第三章变量之间的关系(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览


文档简介
北师版七下数学第三章变量之间的关系
一、选择题
雪橇手从斜坡顶部滑了下来,下图中可以大致刻画出雪橇手下滑过程中速度与时间变化情况的是
A.
B.
C.
D.
对于关系式
,下列说法:①
是自变量,
是因变量;②
的数值可以任意选择;③
是变量,它的值与
无关;④这个关系式表示的变量之间的关系不能用图象表示;⑤
与
的关系还可以用列表格和图象法表示.其中正确的是
A.①②③
B.①②④
C.①②⑤
D.①④⑤
如图所示的图象(折线
)描述了某汽车在行驶过程中速度与时间的关系,下列说法中错误的是
A.第
时汽车的速度是
B.第
时汽车的速度是
C.从第
到第
,汽车行驶了
D.从第
到第
,汽车的速度从
减少到
在物理学中,导线的电阻随温度的变化而变化,有一段导线
时电阻为
欧姆,温度每增加
,电阻会增加
欧姆,则电阻
与温度
的关系是
A.
B.
C.
D.
某工程队修筑A村到B村的公路,前期修筑的是平路,后期修筑的是坡路,修筑的公路长度
()与时间
(天)之间的函数关系如图,则下列结论中错误的是
A.平路长
B.平路上每天修筑
C.坡路长
D.坡路上每天修筑
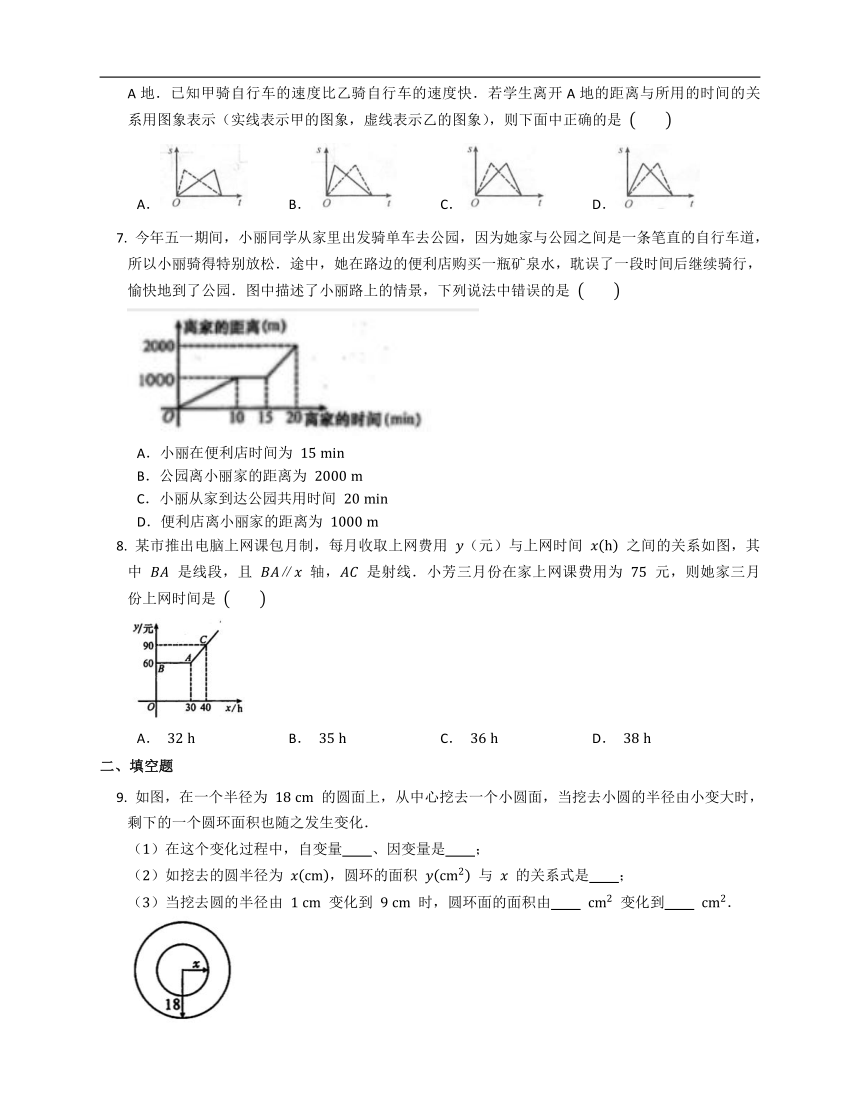
某校举行趣味运动会,甲、乙两名学生同时从A地到B地,甲先骑自行车到B地后跑步回A地,乙先跑步到B地再骑自行车回到A地(骑自行车的速度快于跑步的速度),最后两人恰好同时回到A地.已知甲骑自行车的速度比乙骑自行车的速度快.若学生离开A地的距离与所用的时间的关系用图象表示(实线表示甲的图象,虚线表示乙的图象),则下面中正确的是
A.
B.
C.
D.
今年五一期间,小丽同学从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店购买一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是
A.小丽在便利店时间为
B.公园离小丽家的距离为
C.小丽从家到达公园共用时间
D.便利店离小丽家的距离为
某市推出电脑上网课包月制,每月收取上网费用
(元)与上网时间
之间的关系如图,其中
是线段,且
轴,
是射线.小芳三月份在家上网课费用为
元,则她家三月份上网时间是
A.
B.
C.
D.
二、填空题
如图,在一个半径为
的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.
()在这个变化过程中,自变量
、因变量是
;
()如挖去的圆半径为
,圆环的面积
与
的关系式是
;
()当挖去圆的半径由
变化到
时,圆环面的面积由
变化到
.
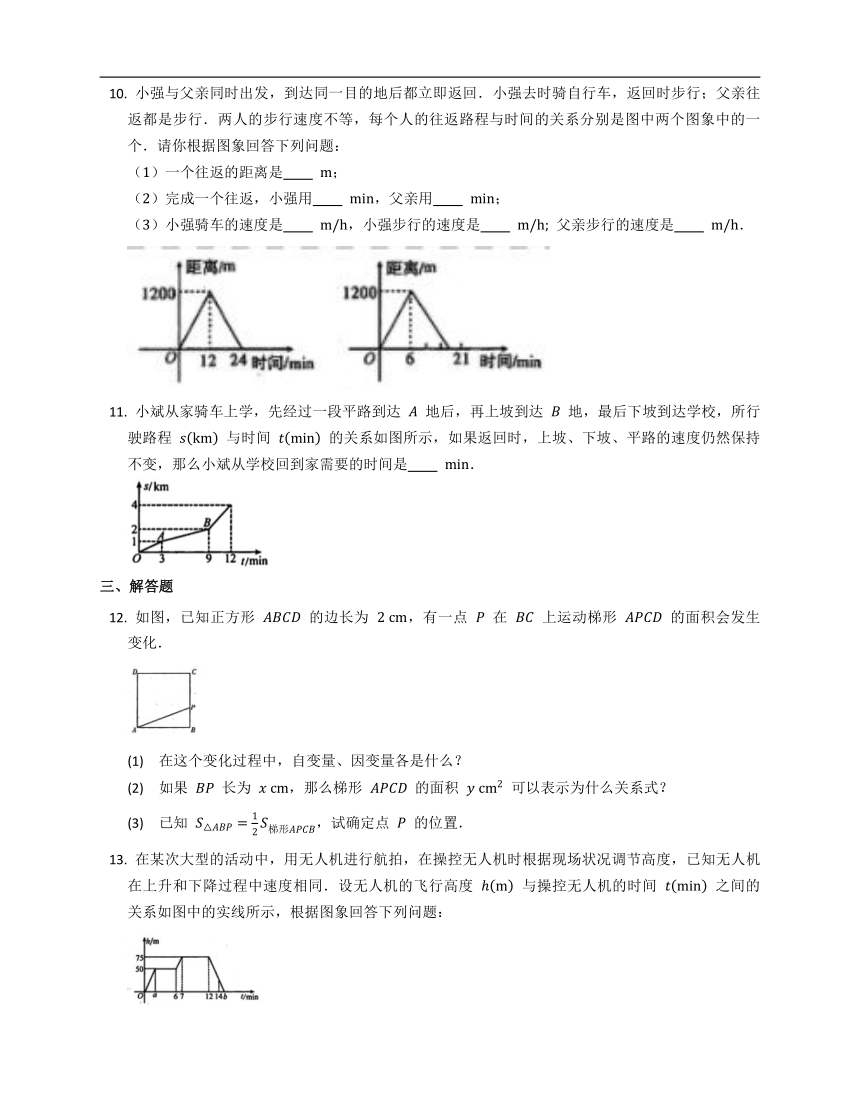
小强与父亲同时出发,到达同一目的地后都立即返回.小强去时骑自行车,返回时步行;父亲往返都是步行.两人的步行速度不等,每个人的往返路程与时间的关系分别是图中两个图象中的一个.请你根据图象回答下列问题:
()一个往返的距离是
;
()完成一个往返,小强用
,父亲用
;
()小强骑车的速度是
,小强步行的速度是
父亲步行的速度是
.
小斌从家骑车上学,先经过一段平路到达
地后,再上坡到达
地,最后下坡到达学校,所行驶路程
与时间
的关系如图所示,如果返回时,上坡、下坡、平路的速度仍然保持不变,那么小斌从学校回到家需要的时间是
.
三、解答题
如图,已知正方形
的边长为
,有一点
在
上运动梯形
的面积会发生变化.
(1)
在这个变化过程中,自变量、因变量各是什么?
(2)
如果
长为
,那么梯形
的面积
可以表示为什么关系式?
(3)
已知
,试确定点
的位置.
在某次大型的活动中,用无人机进行航拍,在操控无人机时根据现场状况调节高度,已知无人机在上升和下降过程中速度相同.设无人机的飞行高度
与操控无人机的时间
之间的关系如图中的实线所示,根据图象回答下列问题:
(1)
图中的自变量是
,因变量是
;
(2)
无人机在
高的上空停留的时间是
;
(3)
在上升或下降过程中,无人机的速度为
;
(4)
图中
表示的数是
;
表示的数是
;
(5)
求第
时无人机的飞行高度是多少米?
绵州大剧院矩形专场音乐会,成人票每张
元,学生票每张
元.暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案
:购买一张成人票赠送一张学生票;方案
:按总价的
付款.某校有
名老师与若干名(不少于
人)学生听音乐会.
(1)
设学生人数为
(人),付款总金额为
(元),分别建立两种优惠方案中
与
的关系式;
(2)
请计算并确定出最节省费用的购票方案.
小红与小兰从学校出发到距学校
的书店买书,下图反应他们两人离开学校的路程与时间的关系.根据图形尝试解决提出的下列问题:
(1)
小红与小兰谁先出发?谁先达到?
(2)
描述小兰离学校的路程与时间的变化关系;
(3)
小兰前
的速度和最后
的速度是多少?怎样从图象上直观地反映速度的大小?
(4)
小红与小兰从学校到书店的平均速度各是多少?
如图(),已知
是三角形
边上的高,且
,
是一个动点,由点
向点
移动,其速度与时间的变化关系如图()所示,已知
.
(1)
当
点在运动过程中,求三角形
的面积
与运动时间
之间的关系式;
(2)
当
点停止后,求
的面积.
如图,正方形
的边长为
,动点
从点
出发,在正方形的边上由
运动,设运动的时间为
(),三角形
的面积为
(),
与
的图象如图.
(1)
求点
在
上运动的时间范围;
(2)
当
为何值时,三角形
的面积为
.
答案
一、选择题
1.
【答案】A
2.
【答案】C
3.
【答案】C
4.
【答案】A
5.
【答案】D
【解析】A.平路长
,正确;
B.平路上每天修筑
,正确;
C.坡路长
,正确;
D.坡路上每天修筑
,错误.
6.
【答案】B
【解析】关键语句是“已知甲骑自行车的速度比乙骑自行车的速度快,最后两人恰好同时回到A地”,
所以表明了乙跑步比甲快,因此综合考虑只能选择B.
7.
【答案】A
8.
【答案】B
【解析】超出
的上网课费用为
(元/时),他家三月份上网时间为:.
二、填空题
9.
【答案】小圆半径;圆环面积;
;
;
10.
【答案】
;
;
;
;
;
11.
【答案】
【解析】根据图象可知:小明从家骑车上学,上坡的路程是
,用
,则上坡速度是
;下坡路长是
,用
,则速度是
,他从学校回到家需要的时间为
.
三、解答题
12.
【答案】
(1)
自变量是
的长度,因变量是梯形
的面积;
(2)
;
(3)
根据等式建立方程,,解得
即点
在距离点
处.
13.
【答案】
(1)
时间(或
);飞行高度(或
)
(2)
(3)
(4)
;
(5)
.
答:第
时无人机的飞行高度是
.
【解析】
(2)
无人机在
高的上空停留的时间是
.
(3)
在上升或下降过程中,无人机的速度
.
(4)
图中
表示的数是
;
表示的数是
.
14.
【答案】
(1)
按优惠方案①可得,,按优惠方案②可得,.
(2)
①当
时,,
当购买
张票时,两种优惠方案付款一样多;
②当
时,,优惠方案①付款较少;
③当
时,,优惠方案②付款较少.
15.
【答案】
(1)
小兰先出发,她们同时到达.
(2)
小兰从学校出发,经
走了
后遇到事情停下来,
后继续出发,最后骑车花
时间与小红同时到达书店.
(3)
小兰前
速度为
,后
速度为
.
(4)
小红平均速度为
,小兰的平均速度为
.
16.
【答案】
(1)
由图()可知,
点的速度为
,
,即
.
(2)
当
点停止后,即
点与
点重合时的面积,
当
时,.
三角形
面积为
.
17.
【答案】
(1)
根据图象得:点
在
上运动的时间范围为
.
(2)
点
在
上时,
三角形
的面积
;
点
在
时,
三角形
的面积
;
点
在
上时,,
三角形
的面积
当
时,,
三角形
的面积为
,即
时,
,;
当
时,,;
当
为
时,三角形
的面积为
.
一、选择题
雪橇手从斜坡顶部滑了下来,下图中可以大致刻画出雪橇手下滑过程中速度与时间变化情况的是
A.
B.
C.
D.
对于关系式
,下列说法:①
是自变量,
是因变量;②
的数值可以任意选择;③
是变量,它的值与
无关;④这个关系式表示的变量之间的关系不能用图象表示;⑤
与
的关系还可以用列表格和图象法表示.其中正确的是
A.①②③
B.①②④
C.①②⑤
D.①④⑤
如图所示的图象(折线
)描述了某汽车在行驶过程中速度与时间的关系,下列说法中错误的是
A.第
时汽车的速度是
B.第
时汽车的速度是
C.从第
到第
,汽车行驶了
D.从第
到第
,汽车的速度从
减少到
在物理学中,导线的电阻随温度的变化而变化,有一段导线
时电阻为
欧姆,温度每增加
,电阻会增加
欧姆,则电阻
与温度
的关系是
A.
B.
C.
D.
某工程队修筑A村到B村的公路,前期修筑的是平路,后期修筑的是坡路,修筑的公路长度
()与时间
(天)之间的函数关系如图,则下列结论中错误的是
A.平路长
B.平路上每天修筑
C.坡路长
D.坡路上每天修筑
某校举行趣味运动会,甲、乙两名学生同时从A地到B地,甲先骑自行车到B地后跑步回A地,乙先跑步到B地再骑自行车回到A地(骑自行车的速度快于跑步的速度),最后两人恰好同时回到A地.已知甲骑自行车的速度比乙骑自行车的速度快.若学生离开A地的距离与所用的时间的关系用图象表示(实线表示甲的图象,虚线表示乙的图象),则下面中正确的是
A.
B.
C.
D.
今年五一期间,小丽同学从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店购买一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是
A.小丽在便利店时间为
B.公园离小丽家的距离为
C.小丽从家到达公园共用时间
D.便利店离小丽家的距离为
某市推出电脑上网课包月制,每月收取上网费用
(元)与上网时间
之间的关系如图,其中
是线段,且
轴,
是射线.小芳三月份在家上网课费用为
元,则她家三月份上网时间是
A.
B.
C.
D.
二、填空题
如图,在一个半径为
的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.
()在这个变化过程中,自变量
、因变量是
;
()如挖去的圆半径为
,圆环的面积
与
的关系式是
;
()当挖去圆的半径由
变化到
时,圆环面的面积由
变化到
.
小强与父亲同时出发,到达同一目的地后都立即返回.小强去时骑自行车,返回时步行;父亲往返都是步行.两人的步行速度不等,每个人的往返路程与时间的关系分别是图中两个图象中的一个.请你根据图象回答下列问题:
()一个往返的距离是
;
()完成一个往返,小强用
,父亲用
;
()小强骑车的速度是
,小强步行的速度是
父亲步行的速度是
.
小斌从家骑车上学,先经过一段平路到达
地后,再上坡到达
地,最后下坡到达学校,所行驶路程
与时间
的关系如图所示,如果返回时,上坡、下坡、平路的速度仍然保持不变,那么小斌从学校回到家需要的时间是
.
三、解答题
如图,已知正方形
的边长为
,有一点
在
上运动梯形
的面积会发生变化.
(1)
在这个变化过程中,自变量、因变量各是什么?
(2)
如果
长为
,那么梯形
的面积
可以表示为什么关系式?
(3)
已知
,试确定点
的位置.
在某次大型的活动中,用无人机进行航拍,在操控无人机时根据现场状况调节高度,已知无人机在上升和下降过程中速度相同.设无人机的飞行高度
与操控无人机的时间
之间的关系如图中的实线所示,根据图象回答下列问题:
(1)
图中的自变量是
,因变量是
;
(2)
无人机在
高的上空停留的时间是
;
(3)
在上升或下降过程中,无人机的速度为
;
(4)
图中
表示的数是
;
表示的数是
;
(5)
求第
时无人机的飞行高度是多少米?
绵州大剧院矩形专场音乐会,成人票每张
元,学生票每张
元.暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案
:购买一张成人票赠送一张学生票;方案
:按总价的
付款.某校有
名老师与若干名(不少于
人)学生听音乐会.
(1)
设学生人数为
(人),付款总金额为
(元),分别建立两种优惠方案中
与
的关系式;
(2)
请计算并确定出最节省费用的购票方案.
小红与小兰从学校出发到距学校
的书店买书,下图反应他们两人离开学校的路程与时间的关系.根据图形尝试解决提出的下列问题:
(1)
小红与小兰谁先出发?谁先达到?
(2)
描述小兰离学校的路程与时间的变化关系;
(3)
小兰前
的速度和最后
的速度是多少?怎样从图象上直观地反映速度的大小?
(4)
小红与小兰从学校到书店的平均速度各是多少?
如图(),已知
是三角形
边上的高,且
,
是一个动点,由点
向点
移动,其速度与时间的变化关系如图()所示,已知
.
(1)
当
点在运动过程中,求三角形
的面积
与运动时间
之间的关系式;
(2)
当
点停止后,求
的面积.
如图,正方形
的边长为
,动点
从点
出发,在正方形的边上由
运动,设运动的时间为
(),三角形
的面积为
(),
与
的图象如图.
(1)
求点
在
上运动的时间范围;
(2)
当
为何值时,三角形
的面积为
.
答案
一、选择题
1.
【答案】A
2.
【答案】C
3.
【答案】C
4.
【答案】A
5.
【答案】D
【解析】A.平路长
,正确;
B.平路上每天修筑
,正确;
C.坡路长
,正确;
D.坡路上每天修筑
,错误.
6.
【答案】B
【解析】关键语句是“已知甲骑自行车的速度比乙骑自行车的速度快,最后两人恰好同时回到A地”,
所以表明了乙跑步比甲快,因此综合考虑只能选择B.
7.
【答案】A
8.
【答案】B
【解析】超出
的上网课费用为
(元/时),他家三月份上网时间为:.
二、填空题
9.
【答案】小圆半径;圆环面积;
;
;
10.
【答案】
;
;
;
;
;
11.
【答案】
【解析】根据图象可知:小明从家骑车上学,上坡的路程是
,用
,则上坡速度是
;下坡路长是
,用
,则速度是
,他从学校回到家需要的时间为
.
三、解答题
12.
【答案】
(1)
自变量是
的长度,因变量是梯形
的面积;
(2)
;
(3)
根据等式建立方程,,解得
即点
在距离点
处.
13.
【答案】
(1)
时间(或
);飞行高度(或
)
(2)
(3)
(4)
;
(5)
.
答:第
时无人机的飞行高度是
.
【解析】
(2)
无人机在
高的上空停留的时间是
.
(3)
在上升或下降过程中,无人机的速度
.
(4)
图中
表示的数是
;
表示的数是
.
14.
【答案】
(1)
按优惠方案①可得,,按优惠方案②可得,.
(2)
①当
时,,
当购买
张票时,两种优惠方案付款一样多;
②当
时,,优惠方案①付款较少;
③当
时,,优惠方案②付款较少.
15.
【答案】
(1)
小兰先出发,她们同时到达.
(2)
小兰从学校出发,经
走了
后遇到事情停下来,
后继续出发,最后骑车花
时间与小红同时到达书店.
(3)
小兰前
速度为
,后
速度为
.
(4)
小红平均速度为
,小兰的平均速度为
.
16.
【答案】
(1)
由图()可知,
点的速度为
,
,即
.
(2)
当
点停止后,即
点与
点重合时的面积,
当
时,.
三角形
面积为
.
17.
【答案】
(1)
根据图象得:点
在
上运动的时间范围为
.
(2)
点
在
上时,
三角形
的面积
;
点
在
时,
三角形
的面积
;
点
在
上时,,
三角形
的面积
当
时,,
三角形
的面积为
,即
时,
,;
当
时,,;
当
为
时,三角形
的面积为
.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
