2020-2021学年黑龙江省九年级(下)开学数学试卷(五四学制)word解析版
文档属性
| 名称 | 2020-2021学年黑龙江省九年级(下)开学数学试卷(五四学制)word解析版 |

|
|
| 格式 | doc | ||
| 文件大小 | 1019.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览



文档简介
2020-2021学年黑龙江省九年级(下)开学数学试卷(五四学制)
一、选择题(每小题3分,共计30分)
1.下列实数中,是无理数的是( )
A.π B. C. D.|﹣2|
2.下列运算正确的是( )
A.a+a=a2 B.a2?a=a2
C.a3÷a2=a (a≠0) D.(a2)3=a5
3.下列4个图案中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
4.对于每一象限内的双曲线y=,y都随x的增大而增大,则m的取值范围是( )
A.m>0 B.m<0 C.m≥0 D.m≤0
5.如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
A. B.
C. D.
6.一辆汽车在坡角为α的坡面上行驶1000米,则它上升的高度为( )米.
A.1000cosα B. C. D.1000sinα
7.某商品经过两次连续降价,每件售价由原来的100元降到了81元.设平均每次降价的百分率为x,则下列方程中正确的是( )
A.100(1+x)2=81 B.81(1+x)2=100
C.100(1﹣x)2=81 D.81(1﹣x)2=100
8.已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
A.= B.= C.= D.=
9.如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12,则△DEF的周长是( )
A.5cm B.6cm C.5cm D.4cm
10.甲、乙两人都从A出发经B地去C地,乙比甲晚出发1分钟,两人同时到达B地,甲在B地停留1分钟,乙在B地停留2分钟,他们行走的路程y(米)与甲行走的时间x(分钟)之间的函数关系如图所示,则下列说法中正确的个数有( )
①甲到B地前的速度为100m/min
②乙从B地出发后的速度为600m/min
③A、C两地间的路程为1000m
④甲乙再次相遇时距离C地300m.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共计30分)
11.将210000用科学记数法表示为 .
12.若函数y=有意义,则自变量x的取值范围是 .
13.计算:= .
14.把多项式m3n﹣mn3分解因式的结果是 .
15.不等式组的解集为 .
16.一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为 度.
17.一个口袋中装有2个红球、2个白球,每个球除颜色外都相同,随机从中一次摸出两球,摸到都是红球的概率是 .
18.如图,已知PA、PB是⊙O的两条切线,A、B为切点,AC是⊙O的直径,若∠P=80°,则∠BAC的度数为 .
19.二次函数y=x2﹣4x+5的图象的对称轴是直线x= .
20.在正方形ABCD中,点E在直线AB上,EF⊥AC于点F,连接EC,EC=5,△EFC的周长为12,则AE的长为 .
三、解答题(其中21-22题各7分,23-24题各8分,25题10分,共计40分)
21.先化简,再求代数式÷(2m﹣)的值,其中m=2cos30°﹣tan45°
22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.(1)在方格纸中画以AB为一边的正方形ABEF,点E、F均在小正方形的顶点上;(2)在方格纸中画以CD为一边的菱形CDGH,点G、H均在小正方形的顶点上,且菱形的面积为15,连接EG,并直接写出线段EG的长.
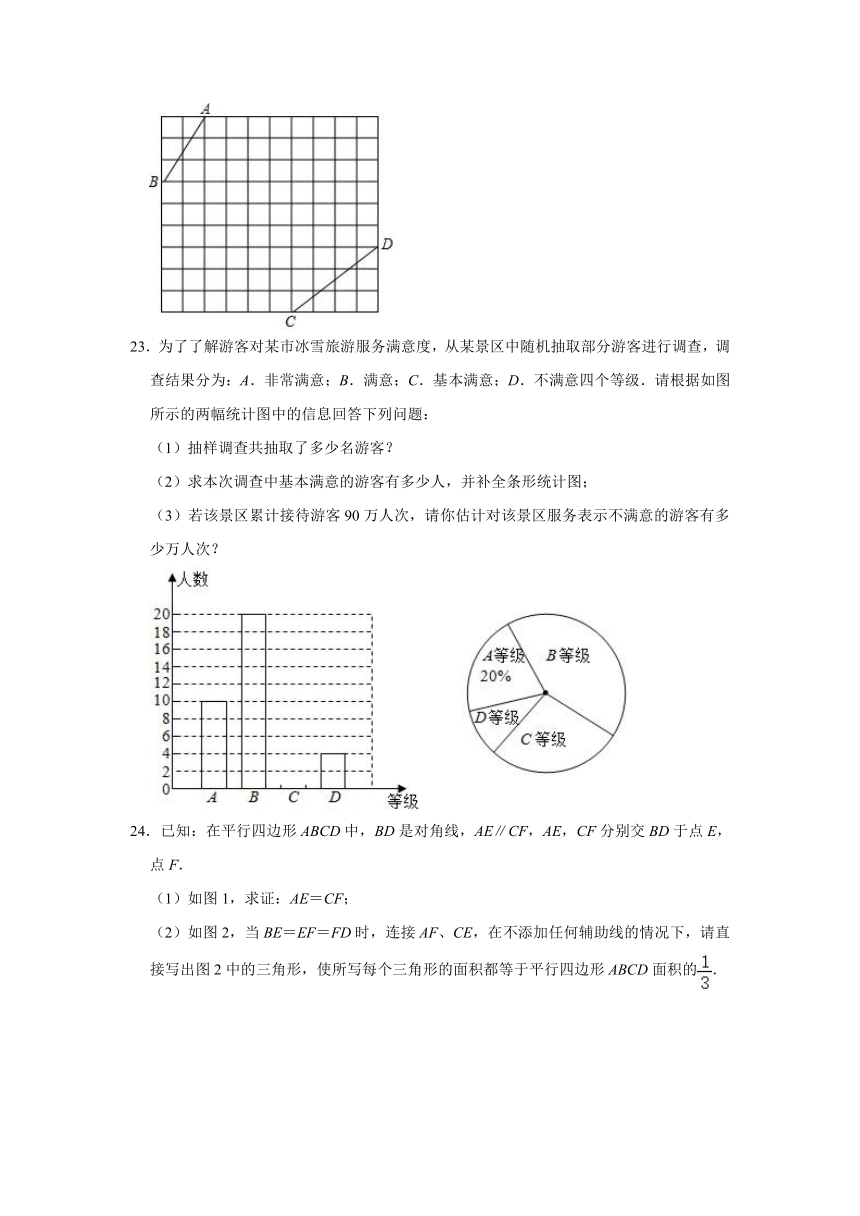
23.为了了解游客对某市冰雪旅游服务满意度,从某景区中随机抽取部分游客进行调查,调查结果分为:A.非常满意;B.满意;C.基本满意;D.不满意四个等级.请根据如图所示的两幅统计图中的信息回答下列问题:
(1)抽样调查共抽取了多少名游客?
(2)求本次调查中基本满意的游客有多少人,并补全条形统计图;
(3)若该景区累计接待游客90万人次,请你估计对该景区服务表示不满意的游客有多少万人次?
24.已知:在平行四边形ABCD中,BD是对角线,AE∥CF,AE,CF分别交BD于点E,点F.
(1)如图1,求证:AE=CF;
(2)如图2,当BE=EF=FD时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中的三角形,使所写每个三角形的面积都等于平行四边形ABCD面积的.
25.小芳去商店购买甲、乙两种商品.现有如下信息:
信息1:甲、乙两种商品的进货单价之和是5元,按零售单价购买甲商品3件和乙商品2件,共付了19元;
信息2:甲商品零售单价比甲进货单价多1元,乙商品零售单价比乙进货单价的2倍少1元.
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)若小芳准备用不超过400元钱购买100件甲、乙两种商品,其中甲种商品至少购买多少件?
2020-2021学年黑龙江省哈尔滨市南岗区萧红中学九年级(下)开学数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
1.下列实数中,是无理数的是( )
A.π B. C. D.|﹣2|
【分析】根据无理数的定义即可判定选择项.
【解答】解:A、是无理数,故本选项符合题意;
B、不是无理数,故本选项不符合题意;
C、不是无理数,故本选项不符合题意;
D、不是无理数,故本选项不符合题意;
故选:A.
2.下列运算正确的是( )
A.a+a=a2 B.a2?a=a2
C.a3÷a2=a (a≠0) D.(a2)3=a5
【分析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=2a,不符合题意;
B、原式=a3,不符合题意;
C、原式=a,符合题意;
D、原式=a6,不符合题意,
故选:C.
3.下列4个图案中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据轴对称图形的概念可得答案.
【解答】解:第二个图形是轴对称图形,
第三个图形是轴对称图形,
轴对称图形的共2个,
故选:B.
4.对于每一象限内的双曲线y=,y都随x的增大而增大,则m的取值范围是( )
A.m>0 B.m<0 C.m≥0 D.m≤0
【分析】根据对于每一象限内的双曲线y=,y都随x的增大而增大和反比例函数的性质可知,m<0,从而可以解答本题.
【解答】解:∵对于每一象限内的双曲线y=,y都随x的增大而增大,
∴m<0,
故选:B.
5.如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
A. B.
C. D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看易得第一层有3个正方形,第二层最右边有一个正方形.
故选:A.
6.一辆汽车在坡角为α的坡面上行驶1000米,则它上升的高度为( )米.
A.1000cosα B. C. D.1000sinα
【分析】根据正弦的定义、坡角的概念计算,得到答案.
【解答】解:设上升的高度为x米,
sinα=,
∴x=1000sinα,
故选:D.
7.某商品经过两次连续降价,每件售价由原来的100元降到了81元.设平均每次降价的百分率为x,则下列方程中正确的是( )
A.100(1+x)2=81 B.81(1+x)2=100
C.100(1﹣x)2=81 D.81(1﹣x)2=100
【分析】设平均每次降价的百分率为x,则等量关系为:原价×(1﹣x)2=现价,据此列方程.
【解答】解:设平均每次降价的百分率为x,
由题意得,100(1﹣x)2=81
故选:C.
8.已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
A.= B.= C.= D.=
【分析】根据相似三角形的判定和性质定理即可得出结论.
【解答】解:∵DE∥BC,EF∥AB,
∴△ADE∽△ABC,△CEF∽△CAB,
∴=,=,==,
故A、B、C选项正确;
∵四边形BDEF是平行四边形,
∴DE=BF,
∴==,故D选项错误;
故选:D.
9.如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12,则△DEF的周长是( )
A.5cm B.6cm C.5cm D.4cm
【分析】根据翻折变换以及E为AB的中点,得出ED∥BC,DE为△ABC的中位线,最后根据△DEF的周长为△ABC周长的一半,即可得出△DEF的周长.
【解答】解:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AE=EF,∠AED=∠FED,
∵E是AB边的中点,
∴AE=EB,
∴BE=EF=AB,
∴∠B=∠BFE=∠AEF=∠AED,
∴ED∥BC,
∵E为AB的中点,
∴DE=BC,D为AC的中点,
∴DF=AD=AC,
∴△DEF的周长为△ABC周长的一半,
即△DEF的周长=×12=6,
故选:B.
10.甲、乙两人都从A出发经B地去C地,乙比甲晚出发1分钟,两人同时到达B地,甲在B地停留1分钟,乙在B地停留2分钟,他们行走的路程y(米)与甲行走的时间x(分钟)之间的函数关系如图所示,则下列说法中正确的个数有( )
①甲到B地前的速度为100m/min
②乙从B地出发后的速度为600m/min
③A、C两地间的路程为1000m
④甲乙再次相遇时距离C地300m.
A.1个 B.2个 C.3个 D.4个
【分析】①②③直接利用图中信息即可解决问题,求出到B地后的函数关系式,利用方程组求交点坐标即可判定④的正确性.
【解答】解:由图象可知:甲到B地前的速度为=100米/分钟,故①正确,
乙从B地出发后的速度为=300米/分钟,故②错误,
由图象可知,A、C两地间的路程为1000米,故③正确,
设甲到B地后的函数关系为y=kx+b,则有
,
解得,
∴y=150x﹣350,
设乙到B地后的函数关系为y=mx+n,则有
,
解得,
∴y=300x﹣1400,
由
解得,
∴甲乙再次相遇时距离A地700米,
∵700﹣400=300,
∴甲乙再次相遇时距离C地300米,故④正确,
故选:C.
二.填空题
11.将210000用科学记数法表示为 2.1×105 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:210000=2.1×105.
故答案为:2.1×105.
12.若函数y=有意义,则自变量x的取值范围是 x≠﹣ .
【分析】根据分式有意义的条件列式计算.
【解答】解:由题意得,4x+1≠0,
解得,x≠﹣,
故答案为:x≠﹣.
13.计算:= .
【分析】直接化简二次根式进而合并得出答案.
【解答】解:原式=2﹣
=.
故答案为:.
14.把多项式m3n﹣mn3分解因式的结果是 mn(m﹣n)(m+n) .
【分析】直接提取公因式mn,进而利用平方差公式分解因式即可.
【解答】解:m3n﹣mn3
=mn(m2﹣n2)
=mn(m+n)(m﹣n).
故答案为:mn(m﹣n)(m+n).
15.不等式组的解集为 ﹣2≤x≤1 .
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式2x+1≤3,得:x≤1,
解不等式5≥3﹣x,得:x≥﹣2,
则不等式组的解集为﹣2≤x≤1,
故答案为:﹣2≤x≤1.
16.一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为 40 度.
【分析】设扇形的圆心角是n°,根据扇形的面积公式即可得到一个关于n的方程,解方程即可求解.
【解答】解:设扇形的圆心角是n°,
根据题意可知:S==π,
解得n=40°,
故答案为40.
17.一个口袋中装有2个红球、2个白球,每个球除颜色外都相同,随机从中一次摸出两球,摸到都是红球的概率是 .
【分析】列表得出所有等可能的情况数,找出都是红球的情况数,即可求出所求的概率.
【解答】解:列表如下:
红 红 白 白
红 ﹣﹣﹣ (红,红) (白,红) (白,红)
红 (红,红) ﹣﹣﹣ (白,红) (白,红)
白 (红,白) (红,白) ﹣﹣﹣ (白,白)
白 (红,白) (红,白) (白,白) ﹣﹣﹣
所有等可能的情况数有12种,其中摸到都是红球的情况有2种,
所以摸到都是红球的概率为=,
故答案为:.
18.如图,已知PA、PB是⊙O的两条切线,A、B为切点,AC是⊙O的直径,若∠P=80°,则∠BAC的度数为 40° .
【分析】先根据切线长定理得到PA=PB,则利用等腰三角形的性质和三角形内角和计算出∠PAB=∠PBA=50°,再根据切线的性质得到∠PAC=90°,然后计算∠PAC﹣∠PAB即可.
【解答】解:∵PA、PB是⊙O的两条切线,A、B为切点,
∴PA=PB,
∴∠PAB=∠PBA=(180°﹣∠P)=(180°﹣80°)=50°,
∵PA为切线,
∴CA⊥AP,
∴∠PAC=90°,
∴∠BAC=∠PAC﹣∠PAB=90°﹣50°=40°.
故答案为40°.
19.二次函数y=x2﹣4x+5的图象的对称轴是直线x= 4 .
【分析】将抛物线解析式转化为顶点式,可求顶点坐标及对称轴.
【解答】解:∵y=x2﹣4x+5=(x﹣4)2﹣3,
∴对称轴为直线x=4,
故答案为:4.
20.在正方形ABCD中,点E在直线AB上,EF⊥AC于点F,连接EC,EC=5,△EFC的周长为12,则AE的长为 3或4 .
【分析】由四边形ABCD是正方形,AC为对角线,得出∠EAF=45°,又因为EF⊥AC,得到∠AFE=90°得出EF=AF,设EF=AF=x,根据△EFC的周长为12,EC=5,得到FC=12﹣x﹣EC=7﹣x,根据勾股定理即可得到结论.
【解答】解:∵四边形ABCD是正方形,AC为对角线,
∴∠EAF=45°,
又∵EF⊥AC,
∴∠AFE=90°,∠AEF=45°,
∴EF=AF,
设EF=AF=x,
∵△EFC的周长为12,EC=5,
∴FC=12﹣x﹣EC=7﹣x,
在Rt△EFC中,EC2=EF2+FC2,
∴52=x2+(7﹣x)2,
解得x=3或x=4.
∴AE=AF=3或4,
故答案为:3或4.
三.解答题(共5小题)
21.先化简,再求代数式÷(2m﹣)的值,其中m=2cos30°﹣tan45°
【分析】先根据分式的混合运算顺序和运算法则化简原式,再根据特殊锐角三角函数值求得m的值,代入计算可得.
【解答】解:原式=÷(﹣)
=÷
=?
=,
∵m=2cos30°﹣tan45°
=2×﹣1
=﹣1,
∴原式===.
22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.(1)在方格纸中画以AB为一边的正方形ABEF,点E、F均在小正方形的顶点上;(2)在方格纸中画以CD为一边的菱形CDGH,点G、H均在小正方形的顶点上,且菱形的面积为15,连接EG,并直接写出线段EG的长.
【分析】(1)根据正方形的性质画出以AB为一边的正方形ABEF即可;
(2)根据菱形的性质画出菱形CDGH,再根据勾股定理求出线段EG的长即可.
【解答】解:(1)如图所示:四边形ABEF即为所求正方形;
(2)如图所示:四边形CDGH或四边形CDG′H′即为所求菱形,
EG==.
23.为了了解游客对某市冰雪旅游服务满意度,从某景区中随机抽取部分游客进行调查,调查结果分为:A.非常满意;B.满意;C.基本满意;D.不满意四个等级.请根据如图所示的两幅统计图中的信息回答下列问题:
(1)抽样调查共抽取了多少名游客?
(2)求本次调查中基本满意的游客有多少人,并补全条形统计图;
(3)若该景区累计接待游客90万人次,请你估计对该景区服务表示不满意的游客有多少万人次?
【分析】(1)根据A的人数除以占的百分比,得出调查总数即可;
(2)将总人数减去A、B、D的人数即可得C的人数,从而补全统计图;
(3)用总人数乘以表示不满意的游客所占的百分比即可.
【解答】解:(1)这次抽样调查的游客有:10÷20%=50(人);
(2)“基本满意”的游客有:50﹣10﹣20﹣4=16(人),
补全条形图如图:
(3)90×=7.2(万人),
答:估计对该景区服务表示不满意的游客有7.2万人次.
24.已知:在平行四边形ABCD中,BD是对角线,AE∥CF,AE,CF分别交BD于点E,点F.
(1)如图1,求证:AE=CF;
(2)如图2,当BE=EF=FD时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中的三角形,使所写每个三角形的面积都等于平行四边形ABCD面积的.
【分析】(1)在平行四边形ABCD中,AD=BC,且AD∥BC,可通过证明△ADE≌△CBF得到AE=CF的结论.
(2)平行四边形ABCD的对角线将其分成两个全等的三角形,点E、F又是对角线BD的三等分点,△ABF、△ADE、△CBF、△CDE的面积都等于平行四边形ABCD面积的.
【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,且AD∥CB,
∴∠ADE=∠CBF;
∵AE∥CF,
∴∠AED=∠CFB,
∴△ADE≌△CBF(AAS),
∴AE=CF.
(2)∵BE=EF=FD,
∴S△ABF=S△ADE=S△ABD,S△CDE=S△CBF=S△CDB,
∵△ABD≌△CDB,
∴S△ABD=S△CDB=S平行四边形ABCD,
∴S△ABF=S△ADE=S△CDE=S△CBF=×S平行四边形ABCD=S平行四边形ABCD.
故答案为:△ABF,△ADE,△CDE,△CBF.
25.小芳去商店购买甲、乙两种商品.现有如下信息:
信息1:甲、乙两种商品的进货单价之和是5元,按零售单价购买甲商品3件和乙商品2件,共付了19元;
信息2:甲商品零售单价比甲进货单价多1元,乙商品零售单价比乙进货单价的2倍少1元.
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)若小芳准备用不超过400元钱购买100件甲、乙两种商品,其中甲种商品至少购买多少件?
【分析】(1)根据题意,列出方程组求解,即可解决问题.
(2)根据题意列出关于m的不等式,即可解决问题.
【解答】解:(1)设甲、乙两种商品的进货单价分别为x、y元.
,
解得:
答:甲、乙两种商品的进货单价分别为2元、3元;
(2)由(1)得:甲商品零售价为x+1=3(元),乙商品零售价为2y﹣1=35(元)
设甲种商品购买m件.
3m+5(100﹣m)≤400,
解得:m≥50,
答;甲种商品至少购买50件.
一、选择题(每小题3分,共计30分)
1.下列实数中,是无理数的是( )
A.π B. C. D.|﹣2|
2.下列运算正确的是( )
A.a+a=a2 B.a2?a=a2
C.a3÷a2=a (a≠0) D.(a2)3=a5
3.下列4个图案中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
4.对于每一象限内的双曲线y=,y都随x的增大而增大,则m的取值范围是( )
A.m>0 B.m<0 C.m≥0 D.m≤0
5.如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
A. B.
C. D.
6.一辆汽车在坡角为α的坡面上行驶1000米,则它上升的高度为( )米.
A.1000cosα B. C. D.1000sinα
7.某商品经过两次连续降价,每件售价由原来的100元降到了81元.设平均每次降价的百分率为x,则下列方程中正确的是( )
A.100(1+x)2=81 B.81(1+x)2=100
C.100(1﹣x)2=81 D.81(1﹣x)2=100
8.已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
A.= B.= C.= D.=
9.如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12,则△DEF的周长是( )
A.5cm B.6cm C.5cm D.4cm
10.甲、乙两人都从A出发经B地去C地,乙比甲晚出发1分钟,两人同时到达B地,甲在B地停留1分钟,乙在B地停留2分钟,他们行走的路程y(米)与甲行走的时间x(分钟)之间的函数关系如图所示,则下列说法中正确的个数有( )
①甲到B地前的速度为100m/min
②乙从B地出发后的速度为600m/min
③A、C两地间的路程为1000m
④甲乙再次相遇时距离C地300m.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共计30分)
11.将210000用科学记数法表示为 .
12.若函数y=有意义,则自变量x的取值范围是 .
13.计算:= .
14.把多项式m3n﹣mn3分解因式的结果是 .
15.不等式组的解集为 .
16.一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为 度.
17.一个口袋中装有2个红球、2个白球,每个球除颜色外都相同,随机从中一次摸出两球,摸到都是红球的概率是 .
18.如图,已知PA、PB是⊙O的两条切线,A、B为切点,AC是⊙O的直径,若∠P=80°,则∠BAC的度数为 .
19.二次函数y=x2﹣4x+5的图象的对称轴是直线x= .
20.在正方形ABCD中,点E在直线AB上,EF⊥AC于点F,连接EC,EC=5,△EFC的周长为12,则AE的长为 .
三、解答题(其中21-22题各7分,23-24题各8分,25题10分,共计40分)
21.先化简,再求代数式÷(2m﹣)的值,其中m=2cos30°﹣tan45°
22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.(1)在方格纸中画以AB为一边的正方形ABEF,点E、F均在小正方形的顶点上;(2)在方格纸中画以CD为一边的菱形CDGH,点G、H均在小正方形的顶点上,且菱形的面积为15,连接EG,并直接写出线段EG的长.
23.为了了解游客对某市冰雪旅游服务满意度,从某景区中随机抽取部分游客进行调查,调查结果分为:A.非常满意;B.满意;C.基本满意;D.不满意四个等级.请根据如图所示的两幅统计图中的信息回答下列问题:
(1)抽样调查共抽取了多少名游客?
(2)求本次调查中基本满意的游客有多少人,并补全条形统计图;
(3)若该景区累计接待游客90万人次,请你估计对该景区服务表示不满意的游客有多少万人次?
24.已知:在平行四边形ABCD中,BD是对角线,AE∥CF,AE,CF分别交BD于点E,点F.
(1)如图1,求证:AE=CF;
(2)如图2,当BE=EF=FD时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中的三角形,使所写每个三角形的面积都等于平行四边形ABCD面积的.
25.小芳去商店购买甲、乙两种商品.现有如下信息:
信息1:甲、乙两种商品的进货单价之和是5元,按零售单价购买甲商品3件和乙商品2件,共付了19元;
信息2:甲商品零售单价比甲进货单价多1元,乙商品零售单价比乙进货单价的2倍少1元.
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)若小芳准备用不超过400元钱购买100件甲、乙两种商品,其中甲种商品至少购买多少件?
2020-2021学年黑龙江省哈尔滨市南岗区萧红中学九年级(下)开学数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
1.下列实数中,是无理数的是( )
A.π B. C. D.|﹣2|
【分析】根据无理数的定义即可判定选择项.
【解答】解:A、是无理数,故本选项符合题意;
B、不是无理数,故本选项不符合题意;
C、不是无理数,故本选项不符合题意;
D、不是无理数,故本选项不符合题意;
故选:A.
2.下列运算正确的是( )
A.a+a=a2 B.a2?a=a2
C.a3÷a2=a (a≠0) D.(a2)3=a5
【分析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=2a,不符合题意;
B、原式=a3,不符合题意;
C、原式=a,符合题意;
D、原式=a6,不符合题意,
故选:C.
3.下列4个图案中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据轴对称图形的概念可得答案.
【解答】解:第二个图形是轴对称图形,
第三个图形是轴对称图形,
轴对称图形的共2个,
故选:B.
4.对于每一象限内的双曲线y=,y都随x的增大而增大,则m的取值范围是( )
A.m>0 B.m<0 C.m≥0 D.m≤0
【分析】根据对于每一象限内的双曲线y=,y都随x的增大而增大和反比例函数的性质可知,m<0,从而可以解答本题.
【解答】解:∵对于每一象限内的双曲线y=,y都随x的增大而增大,
∴m<0,
故选:B.
5.如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
A. B.
C. D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看易得第一层有3个正方形,第二层最右边有一个正方形.
故选:A.
6.一辆汽车在坡角为α的坡面上行驶1000米,则它上升的高度为( )米.
A.1000cosα B. C. D.1000sinα
【分析】根据正弦的定义、坡角的概念计算,得到答案.
【解答】解:设上升的高度为x米,
sinα=,
∴x=1000sinα,
故选:D.
7.某商品经过两次连续降价,每件售价由原来的100元降到了81元.设平均每次降价的百分率为x,则下列方程中正确的是( )
A.100(1+x)2=81 B.81(1+x)2=100
C.100(1﹣x)2=81 D.81(1﹣x)2=100
【分析】设平均每次降价的百分率为x,则等量关系为:原价×(1﹣x)2=现价,据此列方程.
【解答】解:设平均每次降价的百分率为x,
由题意得,100(1﹣x)2=81
故选:C.
8.已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
A.= B.= C.= D.=
【分析】根据相似三角形的判定和性质定理即可得出结论.
【解答】解:∵DE∥BC,EF∥AB,
∴△ADE∽△ABC,△CEF∽△CAB,
∴=,=,==,
故A、B、C选项正确;
∵四边形BDEF是平行四边形,
∴DE=BF,
∴==,故D选项错误;
故选:D.
9.如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12,则△DEF的周长是( )
A.5cm B.6cm C.5cm D.4cm
【分析】根据翻折变换以及E为AB的中点,得出ED∥BC,DE为△ABC的中位线,最后根据△DEF的周长为△ABC周长的一半,即可得出△DEF的周长.
【解答】解:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AE=EF,∠AED=∠FED,
∵E是AB边的中点,
∴AE=EB,
∴BE=EF=AB,
∴∠B=∠BFE=∠AEF=∠AED,
∴ED∥BC,
∵E为AB的中点,
∴DE=BC,D为AC的中点,
∴DF=AD=AC,
∴△DEF的周长为△ABC周长的一半,
即△DEF的周长=×12=6,
故选:B.
10.甲、乙两人都从A出发经B地去C地,乙比甲晚出发1分钟,两人同时到达B地,甲在B地停留1分钟,乙在B地停留2分钟,他们行走的路程y(米)与甲行走的时间x(分钟)之间的函数关系如图所示,则下列说法中正确的个数有( )
①甲到B地前的速度为100m/min
②乙从B地出发后的速度为600m/min
③A、C两地间的路程为1000m
④甲乙再次相遇时距离C地300m.
A.1个 B.2个 C.3个 D.4个
【分析】①②③直接利用图中信息即可解决问题,求出到B地后的函数关系式,利用方程组求交点坐标即可判定④的正确性.
【解答】解:由图象可知:甲到B地前的速度为=100米/分钟,故①正确,
乙从B地出发后的速度为=300米/分钟,故②错误,
由图象可知,A、C两地间的路程为1000米,故③正确,
设甲到B地后的函数关系为y=kx+b,则有
,
解得,
∴y=150x﹣350,
设乙到B地后的函数关系为y=mx+n,则有
,
解得,
∴y=300x﹣1400,
由
解得,
∴甲乙再次相遇时距离A地700米,
∵700﹣400=300,
∴甲乙再次相遇时距离C地300米,故④正确,
故选:C.
二.填空题
11.将210000用科学记数法表示为 2.1×105 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:210000=2.1×105.
故答案为:2.1×105.
12.若函数y=有意义,则自变量x的取值范围是 x≠﹣ .
【分析】根据分式有意义的条件列式计算.
【解答】解:由题意得,4x+1≠0,
解得,x≠﹣,
故答案为:x≠﹣.
13.计算:= .
【分析】直接化简二次根式进而合并得出答案.
【解答】解:原式=2﹣
=.
故答案为:.
14.把多项式m3n﹣mn3分解因式的结果是 mn(m﹣n)(m+n) .
【分析】直接提取公因式mn,进而利用平方差公式分解因式即可.
【解答】解:m3n﹣mn3
=mn(m2﹣n2)
=mn(m+n)(m﹣n).
故答案为:mn(m﹣n)(m+n).
15.不等式组的解集为 ﹣2≤x≤1 .
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式2x+1≤3,得:x≤1,
解不等式5≥3﹣x,得:x≥﹣2,
则不等式组的解集为﹣2≤x≤1,
故答案为:﹣2≤x≤1.
16.一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为 40 度.
【分析】设扇形的圆心角是n°,根据扇形的面积公式即可得到一个关于n的方程,解方程即可求解.
【解答】解:设扇形的圆心角是n°,
根据题意可知:S==π,
解得n=40°,
故答案为40.
17.一个口袋中装有2个红球、2个白球,每个球除颜色外都相同,随机从中一次摸出两球,摸到都是红球的概率是 .
【分析】列表得出所有等可能的情况数,找出都是红球的情况数,即可求出所求的概率.
【解答】解:列表如下:
红 红 白 白
红 ﹣﹣﹣ (红,红) (白,红) (白,红)
红 (红,红) ﹣﹣﹣ (白,红) (白,红)
白 (红,白) (红,白) ﹣﹣﹣ (白,白)
白 (红,白) (红,白) (白,白) ﹣﹣﹣
所有等可能的情况数有12种,其中摸到都是红球的情况有2种,
所以摸到都是红球的概率为=,
故答案为:.
18.如图,已知PA、PB是⊙O的两条切线,A、B为切点,AC是⊙O的直径,若∠P=80°,则∠BAC的度数为 40° .
【分析】先根据切线长定理得到PA=PB,则利用等腰三角形的性质和三角形内角和计算出∠PAB=∠PBA=50°,再根据切线的性质得到∠PAC=90°,然后计算∠PAC﹣∠PAB即可.
【解答】解:∵PA、PB是⊙O的两条切线,A、B为切点,
∴PA=PB,
∴∠PAB=∠PBA=(180°﹣∠P)=(180°﹣80°)=50°,
∵PA为切线,
∴CA⊥AP,
∴∠PAC=90°,
∴∠BAC=∠PAC﹣∠PAB=90°﹣50°=40°.
故答案为40°.
19.二次函数y=x2﹣4x+5的图象的对称轴是直线x= 4 .
【分析】将抛物线解析式转化为顶点式,可求顶点坐标及对称轴.
【解答】解:∵y=x2﹣4x+5=(x﹣4)2﹣3,
∴对称轴为直线x=4,
故答案为:4.
20.在正方形ABCD中,点E在直线AB上,EF⊥AC于点F,连接EC,EC=5,△EFC的周长为12,则AE的长为 3或4 .
【分析】由四边形ABCD是正方形,AC为对角线,得出∠EAF=45°,又因为EF⊥AC,得到∠AFE=90°得出EF=AF,设EF=AF=x,根据△EFC的周长为12,EC=5,得到FC=12﹣x﹣EC=7﹣x,根据勾股定理即可得到结论.
【解答】解:∵四边形ABCD是正方形,AC为对角线,
∴∠EAF=45°,
又∵EF⊥AC,
∴∠AFE=90°,∠AEF=45°,
∴EF=AF,
设EF=AF=x,
∵△EFC的周长为12,EC=5,
∴FC=12﹣x﹣EC=7﹣x,
在Rt△EFC中,EC2=EF2+FC2,
∴52=x2+(7﹣x)2,
解得x=3或x=4.
∴AE=AF=3或4,
故答案为:3或4.
三.解答题(共5小题)
21.先化简,再求代数式÷(2m﹣)的值,其中m=2cos30°﹣tan45°
【分析】先根据分式的混合运算顺序和运算法则化简原式,再根据特殊锐角三角函数值求得m的值,代入计算可得.
【解答】解:原式=÷(﹣)
=÷
=?
=,
∵m=2cos30°﹣tan45°
=2×﹣1
=﹣1,
∴原式===.
22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.(1)在方格纸中画以AB为一边的正方形ABEF,点E、F均在小正方形的顶点上;(2)在方格纸中画以CD为一边的菱形CDGH,点G、H均在小正方形的顶点上,且菱形的面积为15,连接EG,并直接写出线段EG的长.
【分析】(1)根据正方形的性质画出以AB为一边的正方形ABEF即可;
(2)根据菱形的性质画出菱形CDGH,再根据勾股定理求出线段EG的长即可.
【解答】解:(1)如图所示:四边形ABEF即为所求正方形;
(2)如图所示:四边形CDGH或四边形CDG′H′即为所求菱形,
EG==.
23.为了了解游客对某市冰雪旅游服务满意度,从某景区中随机抽取部分游客进行调查,调查结果分为:A.非常满意;B.满意;C.基本满意;D.不满意四个等级.请根据如图所示的两幅统计图中的信息回答下列问题:
(1)抽样调查共抽取了多少名游客?
(2)求本次调查中基本满意的游客有多少人,并补全条形统计图;
(3)若该景区累计接待游客90万人次,请你估计对该景区服务表示不满意的游客有多少万人次?
【分析】(1)根据A的人数除以占的百分比,得出调查总数即可;
(2)将总人数减去A、B、D的人数即可得C的人数,从而补全统计图;
(3)用总人数乘以表示不满意的游客所占的百分比即可.
【解答】解:(1)这次抽样调查的游客有:10÷20%=50(人);
(2)“基本满意”的游客有:50﹣10﹣20﹣4=16(人),
补全条形图如图:
(3)90×=7.2(万人),
答:估计对该景区服务表示不满意的游客有7.2万人次.
24.已知:在平行四边形ABCD中,BD是对角线,AE∥CF,AE,CF分别交BD于点E,点F.
(1)如图1,求证:AE=CF;
(2)如图2,当BE=EF=FD时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中的三角形,使所写每个三角形的面积都等于平行四边形ABCD面积的.
【分析】(1)在平行四边形ABCD中,AD=BC,且AD∥BC,可通过证明△ADE≌△CBF得到AE=CF的结论.
(2)平行四边形ABCD的对角线将其分成两个全等的三角形,点E、F又是对角线BD的三等分点,△ABF、△ADE、△CBF、△CDE的面积都等于平行四边形ABCD面积的.
【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,且AD∥CB,
∴∠ADE=∠CBF;
∵AE∥CF,
∴∠AED=∠CFB,
∴△ADE≌△CBF(AAS),
∴AE=CF.
(2)∵BE=EF=FD,
∴S△ABF=S△ADE=S△ABD,S△CDE=S△CBF=S△CDB,
∵△ABD≌△CDB,
∴S△ABD=S△CDB=S平行四边形ABCD,
∴S△ABF=S△ADE=S△CDE=S△CBF=×S平行四边形ABCD=S平行四边形ABCD.
故答案为:△ABF,△ADE,△CDE,△CBF.
25.小芳去商店购买甲、乙两种商品.现有如下信息:
信息1:甲、乙两种商品的进货单价之和是5元,按零售单价购买甲商品3件和乙商品2件,共付了19元;
信息2:甲商品零售单价比甲进货单价多1元,乙商品零售单价比乙进货单价的2倍少1元.
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)若小芳准备用不超过400元钱购买100件甲、乙两种商品,其中甲种商品至少购买多少件?
【分析】(1)根据题意,列出方程组求解,即可解决问题.
(2)根据题意列出关于m的不等式,即可解决问题.
【解答】解:(1)设甲、乙两种商品的进货单价分别为x、y元.
,
解得:
答:甲、乙两种商品的进货单价分别为2元、3元;
(2)由(1)得:甲商品零售价为x+1=3(元),乙商品零售价为2y﹣1=35(元)
设甲种商品购买m件.
3m+5(100﹣m)≤400,
解得:m≥50,
答;甲种商品至少购买50件.
同课章节目录
