2020-2021学年高中数学人教A版必修5第三章3.2 一元二次不等式及其解法(2)课件(共15张PPT)
文档属性
| 名称 | 2020-2021学年高中数学人教A版必修5第三章3.2 一元二次不等式及其解法(2)课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 23:25:25 | ||
图片预览





文档简介
(共15张PPT)
3.2一元二次不等式及其解法(2)
——一元二次不等式恒成立问题
普通高中课程标准实验教科书
人民教育出版社
A版
数学
必修5
3.2一元二次不等式及其解法---恒成立问题的解决
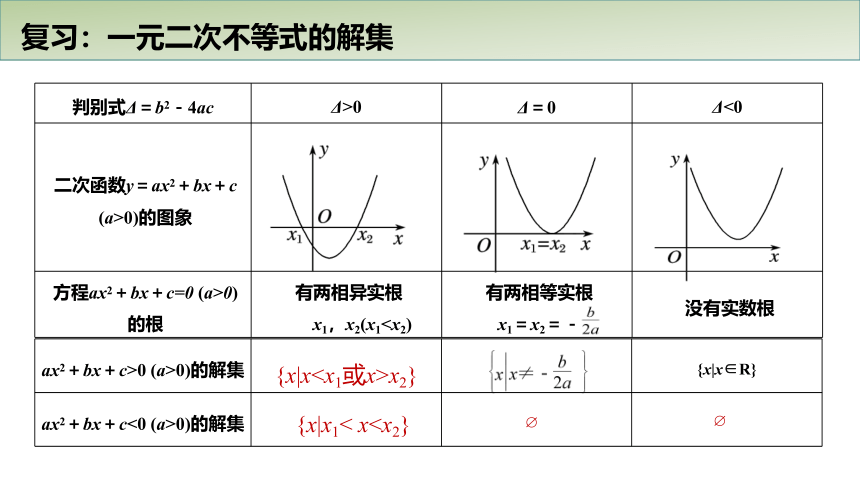
判别式Δ=b2-4ac
Δ>0
Δ=0
Δ<0
二次函数y=ax2+bx+c
(a>0)的图象
?
?
?
方程ax2+bx+c=0
(a>0)
的根
有两相异实根
x1,x2(x1有两相等实根
x1=x2=-
没有实数根
复习:一元二次不等式的解集
ax2+bx+c>0
(a>0)的解集
{x|x∈R}
ax2+bx+c<0
(a>0)的解集
{x|xx2}
{x|x1<
x?
?
一元二次不等式的解法---在R上的恒成立问题
1.一元二次不等式ax2+bx+c>0恒成立的条件是:
探
究
2.一元二次不等式ax2+bx+c
≥
0恒成立的条件是:
3.一元二次不等式ax2+bx+c
<
0恒成立的条件是:
4.一元二次不等式ax2+bx+c
≤
0恒成立的条件是:
O
x
y
一元二次不等式的解法---在R上的恒成立问题
例1 已知函数f?(x)=mx2-mx-1.若对于x∈R,f?(x)<0恒成立,求实数m的取值范围.
当m=0时,f?(x)=-1<0恒成立.
综上,-4解:
“不等式x2-x+m>0在R上恒成立”的充要条件是(
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵不等式x2-x+m>0在R上恒成立,
A
在R上的恒成立问题---练习
练习1
解:
∴不等式x2-x+m>0在R上恒成立,
函数y=f(x)在区间[a,b]上的图象全部在x轴
方.
区间[a,b]
是不等式f(x)>0的解集的
.
恒成立的不等式问题通常转化为求最值问题,即:
f(x)≤k恒成立?
≤k;
f(x)≥k恒成立?
≥k.
一般地,“不等式f(x)>0在区间[a,b]上恒成立”的几何意义是:
上
子集
f(x)max
f(x)min
在给定区间上的恒成立问题
y
x
a
b
O
y=f(x)
例2 已知函数f?(x)=mx2-mx-1.若对于x∈[1,3],f?(x)<5-m恒成立,求实数m的取值范围.
一元二次不等式的解法---在给定区间上恒成立问题
解 要使f?(x)<-m+5在x∈[1,3]上恒成立,
即mx2-mx-1<
-m+5,
【法一】令g(x)=mx2-mx+m-6,
x∈[1,3],
只需求g(x)max即可
当m>0时,
g(x)的对称轴为
,
g(x)在[1,3]上是增函数,
故g(x)max=g(3),
即7m-6<0,
当m<0时,
g(x)在[1,3]上是减函数,
所以g(x)max=g(1),
即m-6<0,
m<6,
所以m<0.
综上所述,m的取值范围是
mx2-mx+m-6<
0,在x∈[1,3]上恒成立.
当m=0时,g(x)=-6<0恒成立;
若将“f?(x)<5-m恒成立”改为“f?(x)<5-m无解”,如何求m的取值范围?
例2 已知函数f?(x)=mx2-mx-1.若对于x∈[1,3],f?(x)<5-m恒成立,求实数m的取值范围.
一元二次不等式的解法---在给定区间上恒成立问题
解
要使f?(x)<-m+5在x∈[1,3]上恒成立,即mx2-mx-1<
-m+5,
mx2-mx+m-6<
0,在x∈[1,3]上恒成立.
【法二】
只需m变式练习
解 若f?(x)<5-m无解,即f?(x)≥5-m恒成立,
只需m≥ymax即可
即m
∈
[6,+∞).
一元二次不等式及其解法---给定参数范围的恒成立问题
例3 若mx2-mx-1<0对于m∈[1,2]恒成立,求实数x的取值范围.
解 设g(m)=mx2-mx-1
=(x2-x)m-1
其图象是直线,当m∈[1,2]时,图象为一条线段,
解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.
(1)若当x∈R时,f?(x)≥a恒成立,求实数a的取值范围;
(2)若当x∈[-2,2]时,f?(x)≥a恒成立,求实数a的取值范围;
(3)若当a∈[4,6]时,f?(x)≥0恒成立,求实数x的取值范围.
三类恒成立问题---跟踪训练
跟踪训练 函数f?(x)=x2+ax+3.
解 ∵当x∈R时,x2+ax+3-a≥0恒成立,
需Δ=a2-4(3-a)≤0,即a2+4a-12≤0,
解得-6≤a≤2,∴实数a的取值范围是[-6,2].
(1)若当x∈R时,f?(x)≥a恒成立,求实数a的取值范围;
跟踪训练 函数f?(x)=x2+ax+3.
解 由题意可转化为x2+ax+3-a≥0在x∈[-2,2]上恒成立,
则(x2+ax+3-a)min≥0(x∈[-2,2]).
令g(x)=x2+ax+3-a,x∈[-2,2],
解得-6≤a≤2,∴-4≤a≤2;
解得a≥-7,∴-7≤a<-4.
综上可得,满足条件的实数a的取值范围是[-7,2].
跟踪训练 函数f?(x)=x2+ax+3.
(2)若当x∈[-2,2]时,f?(x)≥a恒成立,求实数a的取值范围;
(3)若当a∈[4,6]时,f?(x)≥0恒成立,求实数x的取值范围.
解 令h(a)=xa+x2+3.
当a∈[4,6]时,h(a)≥0恒成立.
跟踪训练 函数f?(x)=x2+ax+3.
3.2一元二次不等式及其解法---恒成立问题的解决
借助二次函数图像
转化为求函数最值法
先分离参数,再转化为求函数最值
变换主元法
3.2一元二次不等式及其解法(2)
——一元二次不等式恒成立问题
普通高中课程标准实验教科书
人民教育出版社
A版
数学
必修5
3.2一元二次不等式及其解法---恒成立问题的解决
判别式Δ=b2-4ac
Δ>0
Δ=0
Δ<0
二次函数y=ax2+bx+c
(a>0)的图象
?
?
?
方程ax2+bx+c=0
(a>0)
的根
有两相异实根
x1,x2(x1
x1=x2=-
没有实数根
复习:一元二次不等式的解集
ax2+bx+c>0
(a>0)的解集
{x|x∈R}
ax2+bx+c<0
(a>0)的解集
{x|x
{x|x1<
x
?
一元二次不等式的解法---在R上的恒成立问题
1.一元二次不等式ax2+bx+c>0恒成立的条件是:
探
究
2.一元二次不等式ax2+bx+c
≥
0恒成立的条件是:
3.一元二次不等式ax2+bx+c
<
0恒成立的条件是:
4.一元二次不等式ax2+bx+c
≤
0恒成立的条件是:
O
x
y
一元二次不等式的解法---在R上的恒成立问题
例1 已知函数f?(x)=mx2-mx-1.若对于x∈R,f?(x)<0恒成立,求实数m的取值范围.
当m=0时,f?(x)=-1<0恒成立.
综上,-4
“不等式x2-x+m>0在R上恒成立”的充要条件是(
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵不等式x2-x+m>0在R上恒成立,
A
在R上的恒成立问题---练习
练习1
解:
∴不等式x2-x+m>0在R上恒成立,
函数y=f(x)在区间[a,b]上的图象全部在x轴
方.
区间[a,b]
是不等式f(x)>0的解集的
.
恒成立的不等式问题通常转化为求最值问题,即:
f(x)≤k恒成立?
≤k;
f(x)≥k恒成立?
≥k.
一般地,“不等式f(x)>0在区间[a,b]上恒成立”的几何意义是:
上
子集
f(x)max
f(x)min
在给定区间上的恒成立问题
y
x
a
b
O
y=f(x)
例2 已知函数f?(x)=mx2-mx-1.若对于x∈[1,3],f?(x)<5-m恒成立,求实数m的取值范围.
一元二次不等式的解法---在给定区间上恒成立问题
解 要使f?(x)<-m+5在x∈[1,3]上恒成立,
即mx2-mx-1<
-m+5,
【法一】令g(x)=mx2-mx+m-6,
x∈[1,3],
只需求g(x)max即可
当m>0时,
g(x)的对称轴为
,
g(x)在[1,3]上是增函数,
故g(x)max=g(3),
即7m-6<0,
当m<0时,
g(x)在[1,3]上是减函数,
所以g(x)max=g(1),
即m-6<0,
m<6,
所以m<0.
综上所述,m的取值范围是
mx2-mx+m-6<
0,在x∈[1,3]上恒成立.
当m=0时,g(x)=-6<0恒成立;
若将“f?(x)<5-m恒成立”改为“f?(x)<5-m无解”,如何求m的取值范围?
例2 已知函数f?(x)=mx2-mx-1.若对于x∈[1,3],f?(x)<5-m恒成立,求实数m的取值范围.
一元二次不等式的解法---在给定区间上恒成立问题
解
要使f?(x)<-m+5在x∈[1,3]上恒成立,即mx2-mx-1<
-m+5,
mx2-mx+m-6<
0,在x∈[1,3]上恒成立.
【法二】
只需m
解 若f?(x)<5-m无解,即f?(x)≥5-m恒成立,
只需m≥ymax即可
即m
∈
[6,+∞).
一元二次不等式及其解法---给定参数范围的恒成立问题
例3 若mx2-mx-1<0对于m∈[1,2]恒成立,求实数x的取值范围.
解 设g(m)=mx2-mx-1
=(x2-x)m-1
其图象是直线,当m∈[1,2]时,图象为一条线段,
解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.
(1)若当x∈R时,f?(x)≥a恒成立,求实数a的取值范围;
(2)若当x∈[-2,2]时,f?(x)≥a恒成立,求实数a的取值范围;
(3)若当a∈[4,6]时,f?(x)≥0恒成立,求实数x的取值范围.
三类恒成立问题---跟踪训练
跟踪训练 函数f?(x)=x2+ax+3.
解 ∵当x∈R时,x2+ax+3-a≥0恒成立,
需Δ=a2-4(3-a)≤0,即a2+4a-12≤0,
解得-6≤a≤2,∴实数a的取值范围是[-6,2].
(1)若当x∈R时,f?(x)≥a恒成立,求实数a的取值范围;
跟踪训练 函数f?(x)=x2+ax+3.
解 由题意可转化为x2+ax+3-a≥0在x∈[-2,2]上恒成立,
则(x2+ax+3-a)min≥0(x∈[-2,2]).
令g(x)=x2+ax+3-a,x∈[-2,2],
解得-6≤a≤2,∴-4≤a≤2;
解得a≥-7,∴-7≤a<-4.
综上可得,满足条件的实数a的取值范围是[-7,2].
跟踪训练 函数f?(x)=x2+ax+3.
(2)若当x∈[-2,2]时,f?(x)≥a恒成立,求实数a的取值范围;
(3)若当a∈[4,6]时,f?(x)≥0恒成立,求实数x的取值范围.
解 令h(a)=xa+x2+3.
当a∈[4,6]时,h(a)≥0恒成立.
跟踪训练 函数f?(x)=x2+ax+3.
3.2一元二次不等式及其解法---恒成立问题的解决
借助二次函数图像
转化为求函数最值法
先分离参数,再转化为求函数最值
变换主元法
