六年级数学下册课件-2.3圆柱的侧面积和表面积练习 - 苏教版(共63张PPT)
文档属性
| 名称 | 六年级数学下册课件-2.3圆柱的侧面积和表面积练习 - 苏教版(共63张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 06:21:12 | ||
图片预览










文档简介
侧面积和表面积
练习
知识回顾
基本练习
圆柱的底面积=半径2×圆周率
圆柱的侧面积=底面周长×高
圆柱的表面积=侧面积+底面积×2
圆柱的侧面积怎样计算?
底面积怎样计算?
表面积怎样计算?
基本练习
计算下面圆柱的侧面积。(只列式)
底面直径是2米,高1米。
底面半径3分米,高0.1分米。
底面周长31.4厘米,高10厘米。
31.4×10
2×3.14×1
3×2×3.14×0.1
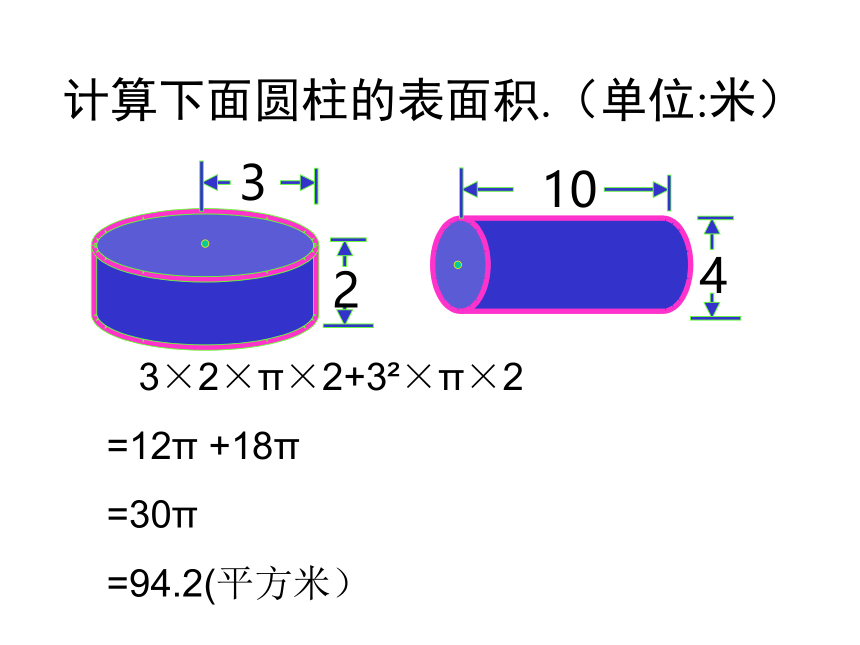
计算下面圆柱的表面积.(单位:米)
3
2
10
4
3×2×π×2+3?×π×2
=12π +18π
=30π
=94.2(平方米)
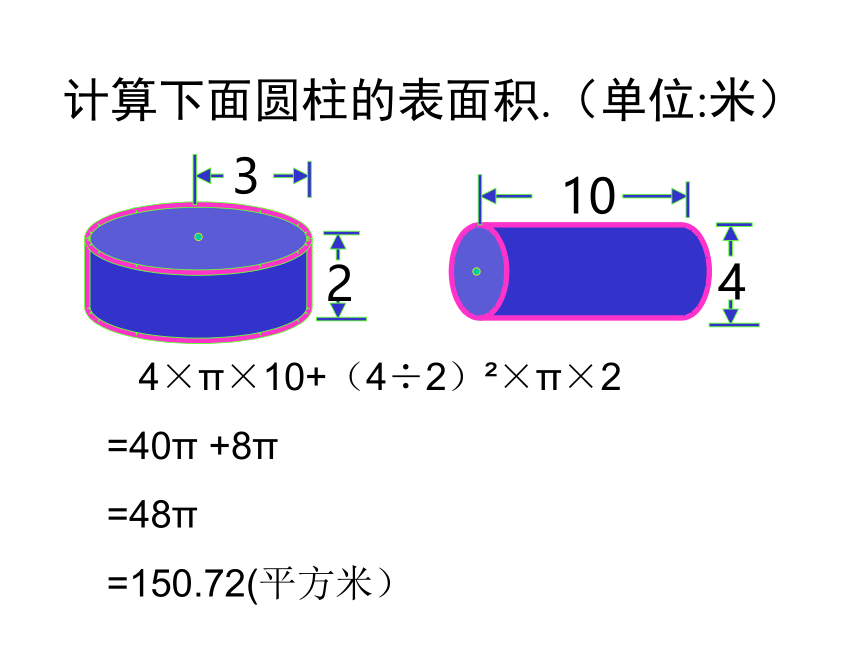
计算下面圆柱的表面积.(单位:米)
3
2
10
4
4×π×10+(4÷2)?×π×2
=40π +8π
=48π
=150.72(平方米)
生活应用
请同学们联系生活实际,说说生活中的这些圆柱体与哪些面积有关?
(1)圆形水池的占地面积;
(2)做一节烟囱所需铁皮的面积;
底面积
侧面积
请同学们联系生活实际,说说生活中的这些圆柱体与哪些面积有关?
一个底面积和侧面积
两个底面积和侧面积
(3)做一个无盖水桶所需铁皮的面积;
(4)做一个油桶所需铁皮的面积;
(5)求易拉罐上商标纸的面积;
侧面积
9、一个圆柱形铁皮水桶,上面没有盖,高是6分米,底面半径是1.8分米。做这个水桶大约要用铁皮多少平方分米?
1.8×2×π×6+1.8? ×π
=21.6π+3.24π
=24.84π
=77.9976(平方分米)
博士帽由圆柱侧面积+
正方形面积组成
10、下图中的“博士帽”是用黑色卡纸做成的,上面是边长30厘米的正方形,下面是底面直径16厘米、高10厘米的无底无盖的圆柱。制作20顶这样的“博士帽”,至少需要多少平方分米黑色卡纸?
(30×30+16×π×10)×20
=(900+160π)×20
=1402.4×20=28048(平方厘米)
=280.48(平方分米)
10、下图中的“博士帽”是用黑色卡纸做成的,上面是边长30厘米的正方形,下面是底面直径16厘米、高10厘米的无底无盖的圆柱。制作20顶这样的“博士帽”,至少需要多少平方分米黑色卡纸?
修建一个圆柱形的沼气池,底面直径是3米,深2米。在池的内壁与下底面抹上水泥,抹水泥部分的面积是多少平方米?
3×π×2+(3÷2)?×π
=6×π +2.25×π
=8.25×π
=25.905(平方米)
一台压路机,前轮底面直径是0.8米,宽2米。前轮转动一周,压路的面积是多少?
0.8×π×2
=1.6×π
=5.024(平方米)
答:压路的面积是5.024平方米.
下图中有10根同样的圆柱形木柱,每根高5米,底面直径是0.2米。如果每平方米需要红色油漆0.3千克,漆这些木柱需油漆多少千克?
下图中有10根同样的圆柱形木柱,每根高5米,底面直径是0.2米。如果每平方米需要红色油漆0.3千克,漆这些木柱需油漆多少千克?
0.2×π×5×10×0.3
=3×π 答:漆这些木柱需
=9.42(千克) 油漆9.42千克。
思维延伸
有一个长5厘米,宽4厘米的长方形,以它的长所在的直线为轴旋转一周,形成图形的表面积是多少平方厘米?
5cm
4cm
5cm
4cm
4cm
5cm
有一个长5厘米,宽4厘米的长方形,以它的长所在的直线为轴旋转一周,形成图形的表面积是多少平方厘米?
4×2×π×5+4?×π×2
=40×π+32×π
=72×π 答:形成图形的表面积.
=226.08(平方厘米)是226.08平方厘米
4cm
5cm
5dm
5dm
5dm
如果将这个正方体切削成最大的圆柱,
这个圆柱的表面积是多少?
5×π×5 +(5÷2)?×π×2
=25×π+12.5×π
=37.5×π
=117.75(平方分米)
逆向思考
一个圆柱形粮仓的侧面积
是251.2平方米,底面半径是2
米。这个粮仓的高是多少米?
251.2÷(2×2×π)
=(251.2÷π)÷(2×2×π ÷π)
=80÷4
=20(米)答:这个粮仓的高是20米.
做一节长15分米,侧面积是47.1平方分米的圆柱形烟囱。这节圆柱形烟囱的底面半径是多少分米?
47.1÷15
=3.14(分米)
3.14÷π÷2
=1÷2
=0.5(分米)
答:这节圆柱形烟囱的底面半径是0.5分米.
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是圆柱.截开后,表面积增加多少平方厘米?像这样截成4段、5段呢?
截成2段表面积增加了
两个底面积
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是圆柱.截开后,表面积增加多少平方厘米?像这样截成4段、5段呢?
(20÷2)?× π×4
=100×π×4
=400π
=1256(平方厘米)
答:截成3段,表面积增加1256平方厘米
截成3段表面积增加
四个底面积
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是圆柱.截开后,表面积增加多少平方厘米?像这样截成4段、5段呢?
(20÷2)?× π×6
=100×π×6
=600π
=1884(平方厘米)
答:截成4段,表面积增加1884平方厘米
截成4段表面积增加
六个底面积
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是圆柱.截开后,表面积增加多少平方厘米?像这样截成4段、5段呢?
(20÷2)?× π×8
=100×π×8
=800π
=2512(平方厘米)
答:截成5段,表面积增加2512平方厘米
截成5段表面积增加
八个底面积
A: 6
B:12
C:24
一个圆柱形木棒,底面直径4厘米,高3厘米,沿底面直径纵剖后,表面积之和增加( )平方厘米。
C
如下图,一个圆柱体被截去10厘米长后,圆柱的表面积减少了62.8平方厘米,求原来圆柱体的侧面积。
10cm
25cm
挑战自我
62.8÷10× 25
=6.28× 25
=157(平方厘米)
答:原来圆柱体的侧面积是157平方厘米。
底面周长
底面周长
高
高
6.28×6.28+(6.28÷π÷2)?×π×2
=39.4384+1×π×2
=39.4384+6.28
=45.7184(平方厘米)
答:这个圆柱的表面积是45.7184平方厘米
8×π×5+5×π×5
+(8÷2)?×π×2
=40π+25π+32π
=97π
=304.58(平方厘米)
答:需要漆304.58平方厘米
6×π×4÷2 +(6÷2)?×π+ 6×4
=12π+9π+24
=21π+24
=89.94(cm?)
2
6
4
想想办法求它的体积。
(单位:cm)
(2÷2)?×π×(4+6)÷2
=1×π×5
=5π
=15.7(cm3)
将一根长4米圆木沿着直径劈成相等的两半,表面积增加了0.8平方米,圆木原来的侧面积是多少?
0.8÷2÷4×π×4
=0.1×π×4
=0.4π
=1.256(m?)
答:圆木原来的侧面积是1.256m?。
2×π×6÷2 +(2÷2)?×π
=6π+π
=7π=21.98(m?)
答:至少需要薄膜21.98平方米。
6×π×1 +(6÷2)?×π
=6π+9π
=15π=47.1(m?)
答:水池与水接触的面积是47.1平方米。
一个圆柱被截去5厘米后,圆柱的表面积减少了31.4平方厘米,求原圆柱的表面积是多少平方厘米?
20厘米
5厘米
1×2×π×20 +1?×π×2
=40π+2π
=42π=131.88(cm? )
答:原圆柱表面积是131.88cm?。
31.4÷5÷π÷2=1( cm)
如下图,把一个高是3厘米,底面直径是4厘米的圆柱沿直径竖切两刀,求1/4圆柱的表面积。
4×π×3÷4 +(4÷2)?×π÷2+ 4×3
=3π+2π+12
=5π+12
=15.7+12
=27.7(cm?)
在棱长5厘米的正方体中间挖去一个直径
2厘米的孔,求剩余部分的表面积。
表面积计算及相关变化
表面积=正方体表面积-两个圆的面积
+圆柱侧面积
5 x5x6 -(2÷2)?×π×2 +2xπx5
=150—2π+10 π
=150—8π
=150—25.12
=124.88(cm2)
如图所示的物体,由三个圆柱体组成的,每个圆柱体的高都是1米,底面半径分别是1.5米,1米和0.5米。如果用红油漆涂它的表面(底面也涂),则涂漆的部分是多少平方米?
分析:利用平移的思想,将小圆柱的顶面
平移到中圆柱的顶面,合起来的顶面再平
移到大圆柱的顶面,这样就相当于是大圆
柱的顶面是完整的。
如图所示的物体,由三个圆柱体组成的,每个圆柱体的高都是1米,底面半径分别是1.5米,1米和0.5米。如果用红油漆涂它的表面(底面也涂),则涂漆的部分是多少平方米?
涂漆部分面积=大表面积
+中侧面积+小侧面积
三个侧面积 :2×0.5×π×1
+2×1×π×1+2×1.5×π×1=6π
大圆柱两个底面积:1.52×π×2=4.5π
表面积:6π+4.5π
=10.5π
=32.97(m2)
练习
知识回顾
基本练习
圆柱的底面积=半径2×圆周率
圆柱的侧面积=底面周长×高
圆柱的表面积=侧面积+底面积×2
圆柱的侧面积怎样计算?
底面积怎样计算?
表面积怎样计算?
基本练习
计算下面圆柱的侧面积。(只列式)
底面直径是2米,高1米。
底面半径3分米,高0.1分米。
底面周长31.4厘米,高10厘米。
31.4×10
2×3.14×1
3×2×3.14×0.1
计算下面圆柱的表面积.(单位:米)
3
2
10
4
3×2×π×2+3?×π×2
=12π +18π
=30π
=94.2(平方米)
计算下面圆柱的表面积.(单位:米)
3
2
10
4
4×π×10+(4÷2)?×π×2
=40π +8π
=48π
=150.72(平方米)
生活应用
请同学们联系生活实际,说说生活中的这些圆柱体与哪些面积有关?
(1)圆形水池的占地面积;
(2)做一节烟囱所需铁皮的面积;
底面积
侧面积
请同学们联系生活实际,说说生活中的这些圆柱体与哪些面积有关?
一个底面积和侧面积
两个底面积和侧面积
(3)做一个无盖水桶所需铁皮的面积;
(4)做一个油桶所需铁皮的面积;
(5)求易拉罐上商标纸的面积;
侧面积
9、一个圆柱形铁皮水桶,上面没有盖,高是6分米,底面半径是1.8分米。做这个水桶大约要用铁皮多少平方分米?
1.8×2×π×6+1.8? ×π
=21.6π+3.24π
=24.84π
=77.9976(平方分米)
博士帽由圆柱侧面积+
正方形面积组成
10、下图中的“博士帽”是用黑色卡纸做成的,上面是边长30厘米的正方形,下面是底面直径16厘米、高10厘米的无底无盖的圆柱。制作20顶这样的“博士帽”,至少需要多少平方分米黑色卡纸?
(30×30+16×π×10)×20
=(900+160π)×20
=1402.4×20=28048(平方厘米)
=280.48(平方分米)
10、下图中的“博士帽”是用黑色卡纸做成的,上面是边长30厘米的正方形,下面是底面直径16厘米、高10厘米的无底无盖的圆柱。制作20顶这样的“博士帽”,至少需要多少平方分米黑色卡纸?
修建一个圆柱形的沼气池,底面直径是3米,深2米。在池的内壁与下底面抹上水泥,抹水泥部分的面积是多少平方米?
3×π×2+(3÷2)?×π
=6×π +2.25×π
=8.25×π
=25.905(平方米)
一台压路机,前轮底面直径是0.8米,宽2米。前轮转动一周,压路的面积是多少?
0.8×π×2
=1.6×π
=5.024(平方米)
答:压路的面积是5.024平方米.
下图中有10根同样的圆柱形木柱,每根高5米,底面直径是0.2米。如果每平方米需要红色油漆0.3千克,漆这些木柱需油漆多少千克?
下图中有10根同样的圆柱形木柱,每根高5米,底面直径是0.2米。如果每平方米需要红色油漆0.3千克,漆这些木柱需油漆多少千克?
0.2×π×5×10×0.3
=3×π 答:漆这些木柱需
=9.42(千克) 油漆9.42千克。
思维延伸
有一个长5厘米,宽4厘米的长方形,以它的长所在的直线为轴旋转一周,形成图形的表面积是多少平方厘米?
5cm
4cm
5cm
4cm
4cm
5cm
有一个长5厘米,宽4厘米的长方形,以它的长所在的直线为轴旋转一周,形成图形的表面积是多少平方厘米?
4×2×π×5+4?×π×2
=40×π+32×π
=72×π 答:形成图形的表面积.
=226.08(平方厘米)是226.08平方厘米
4cm
5cm
5dm
5dm
5dm
如果将这个正方体切削成最大的圆柱,
这个圆柱的表面积是多少?
5×π×5 +(5÷2)?×π×2
=25×π+12.5×π
=37.5×π
=117.75(平方分米)
逆向思考
一个圆柱形粮仓的侧面积
是251.2平方米,底面半径是2
米。这个粮仓的高是多少米?
251.2÷(2×2×π)
=(251.2÷π)÷(2×2×π ÷π)
=80÷4
=20(米)答:这个粮仓的高是20米.
做一节长15分米,侧面积是47.1平方分米的圆柱形烟囱。这节圆柱形烟囱的底面半径是多少分米?
47.1÷15
=3.14(分米)
3.14÷π÷2
=1÷2
=0.5(分米)
答:这节圆柱形烟囱的底面半径是0.5分米.
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是圆柱.截开后,表面积增加多少平方厘米?像这样截成4段、5段呢?
截成2段表面积增加了
两个底面积
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是圆柱.截开后,表面积增加多少平方厘米?像这样截成4段、5段呢?
(20÷2)?× π×4
=100×π×4
=400π
=1256(平方厘米)
答:截成3段,表面积增加1256平方厘米
截成3段表面积增加
四个底面积
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是圆柱.截开后,表面积增加多少平方厘米?像这样截成4段、5段呢?
(20÷2)?× π×6
=100×π×6
=600π
=1884(平方厘米)
答:截成4段,表面积增加1884平方厘米
截成4段表面积增加
六个底面积
一根圆柱形木料,底面直径是20厘米,长是1.8米。把它截成3段,使每一段的形状都是圆柱.截开后,表面积增加多少平方厘米?像这样截成4段、5段呢?
(20÷2)?× π×8
=100×π×8
=800π
=2512(平方厘米)
答:截成5段,表面积增加2512平方厘米
截成5段表面积增加
八个底面积
A: 6
B:12
C:24
一个圆柱形木棒,底面直径4厘米,高3厘米,沿底面直径纵剖后,表面积之和增加( )平方厘米。
C
如下图,一个圆柱体被截去10厘米长后,圆柱的表面积减少了62.8平方厘米,求原来圆柱体的侧面积。
10cm
25cm
挑战自我
62.8÷10× 25
=6.28× 25
=157(平方厘米)
答:原来圆柱体的侧面积是157平方厘米。
底面周长
底面周长
高
高
6.28×6.28+(6.28÷π÷2)?×π×2
=39.4384+1×π×2
=39.4384+6.28
=45.7184(平方厘米)
答:这个圆柱的表面积是45.7184平方厘米
8×π×5+5×π×5
+(8÷2)?×π×2
=40π+25π+32π
=97π
=304.58(平方厘米)
答:需要漆304.58平方厘米
6×π×4÷2 +(6÷2)?×π+ 6×4
=12π+9π+24
=21π+24
=89.94(cm?)
2
6
4
想想办法求它的体积。
(单位:cm)
(2÷2)?×π×(4+6)÷2
=1×π×5
=5π
=15.7(cm3)
将一根长4米圆木沿着直径劈成相等的两半,表面积增加了0.8平方米,圆木原来的侧面积是多少?
0.8÷2÷4×π×4
=0.1×π×4
=0.4π
=1.256(m?)
答:圆木原来的侧面积是1.256m?。
2×π×6÷2 +(2÷2)?×π
=6π+π
=7π=21.98(m?)
答:至少需要薄膜21.98平方米。
6×π×1 +(6÷2)?×π
=6π+9π
=15π=47.1(m?)
答:水池与水接触的面积是47.1平方米。
一个圆柱被截去5厘米后,圆柱的表面积减少了31.4平方厘米,求原圆柱的表面积是多少平方厘米?
20厘米
5厘米
1×2×π×20 +1?×π×2
=40π+2π
=42π=131.88(cm? )
答:原圆柱表面积是131.88cm?。
31.4÷5÷π÷2=1( cm)
如下图,把一个高是3厘米,底面直径是4厘米的圆柱沿直径竖切两刀,求1/4圆柱的表面积。
4×π×3÷4 +(4÷2)?×π÷2+ 4×3
=3π+2π+12
=5π+12
=15.7+12
=27.7(cm?)
在棱长5厘米的正方体中间挖去一个直径
2厘米的孔,求剩余部分的表面积。
表面积计算及相关变化
表面积=正方体表面积-两个圆的面积
+圆柱侧面积
5 x5x6 -(2÷2)?×π×2 +2xπx5
=150—2π+10 π
=150—8π
=150—25.12
=124.88(cm2)
如图所示的物体,由三个圆柱体组成的,每个圆柱体的高都是1米,底面半径分别是1.5米,1米和0.5米。如果用红油漆涂它的表面(底面也涂),则涂漆的部分是多少平方米?
分析:利用平移的思想,将小圆柱的顶面
平移到中圆柱的顶面,合起来的顶面再平
移到大圆柱的顶面,这样就相当于是大圆
柱的顶面是完整的。
如图所示的物体,由三个圆柱体组成的,每个圆柱体的高都是1米,底面半径分别是1.5米,1米和0.5米。如果用红油漆涂它的表面(底面也涂),则涂漆的部分是多少平方米?
涂漆部分面积=大表面积
+中侧面积+小侧面积
三个侧面积 :2×0.5×π×1
+2×1×π×1+2×1.5×π×1=6π
大圆柱两个底面积:1.52×π×2=4.5π
表面积:6π+4.5π
=10.5π
=32.97(m2)
