1.1.1回归分析的基本思想及其初步应用(1)
文档属性
| 名称 | 1.1.1回归分析的基本思想及其初步应用(1) |  | |
| 格式 | zip | ||
| 文件大小 | 201.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-15 23:24:22 | ||
图片预览








文档简介
(共31张PPT)
1.1.1回归分析的基本思想及其初步应用
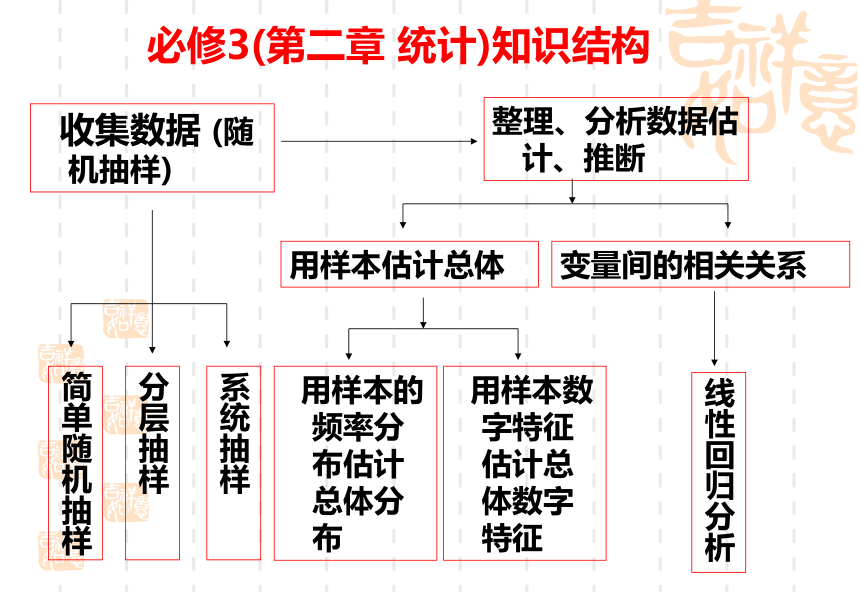
必修3(第二章 统计)知识结构
收集数据 (随机抽样)
整理、分析数据估计、推断
简单随机抽样
分层抽样
系统抽样
用样本估计总体
变量间的相关关系
用样本的频率分布估计总体分布
用样本数字特征估计总体数字特征
线性回归分析
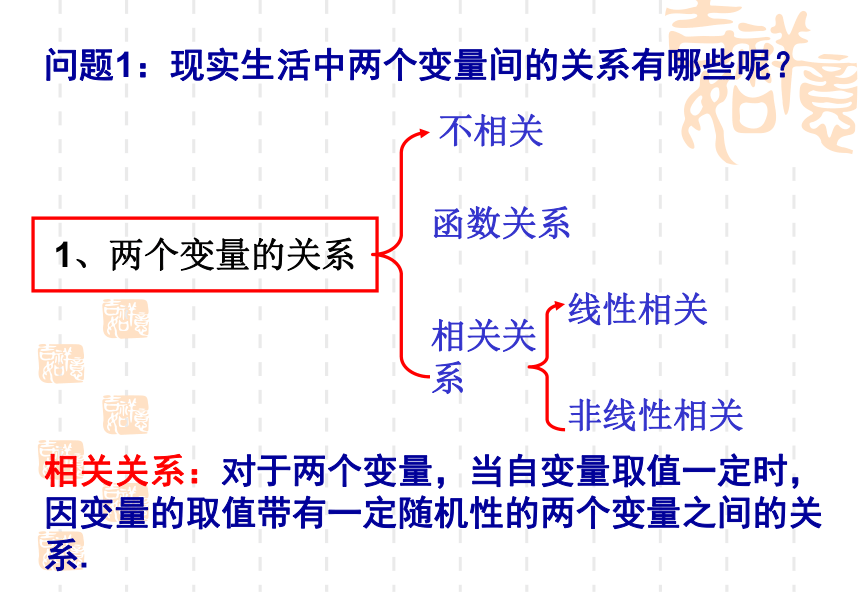
1、两个变量的关系
不相关
相关关系
函数关系
线性相关
非线性相关
问题1:现实生活中两个变量间的关系有哪些呢?
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系.
思考:相关关系与函数关系有怎样的不同?
函数关系中的两个变量间是一种确定性关系
相关关系是一种非确定性关系
函数关系是一种理想的关系模型
相关关系在现实生活中大量存在,是更一般的情况
问题2:对于线性相关的两个变量用什么方法来刻划之间的关系呢?
2、最小二乘估计
最小二乘估计下的线性回归方程:
回归直线必过样本点的中心
3、回归分析的基本步骤:
画散点图
求回归直线方程
预报、决策
这种方法称为回归分析.
回归分析是对具有相关关系的两个变量进行统计
分析的一种常用方法.
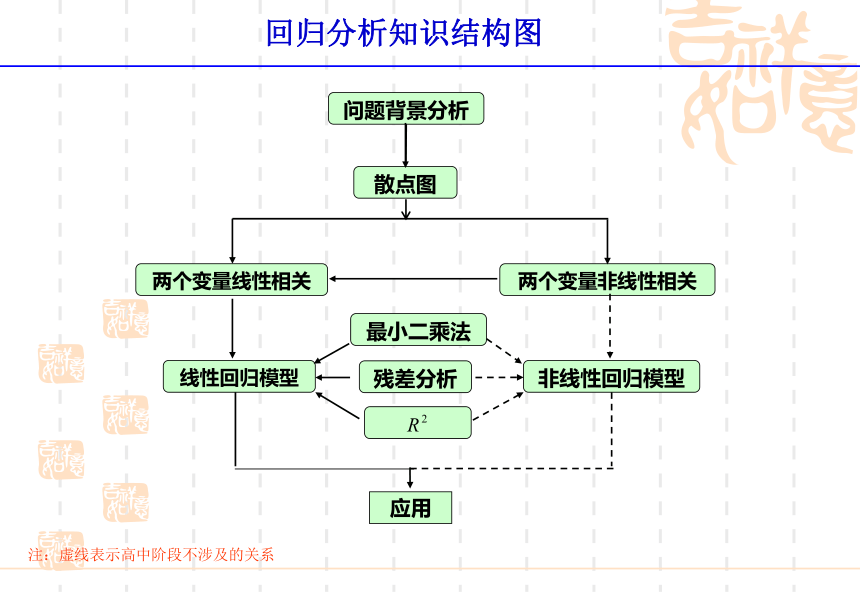
回归分析知识结构图
问题背景分析
线性回归模型
两个变量线性相关
最小二乘法
两个变量非线性相关
非线性回归模型
残差分析
散点图
应用
注:虚线表示高中阶段不涉及的关系
教学情境设计
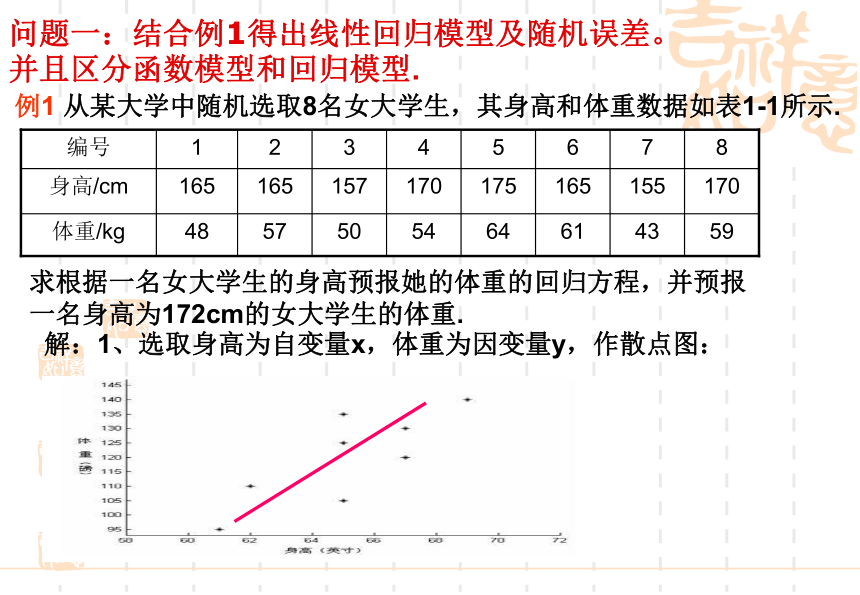
问题一:结合例1得出线性回归模型及随机误差。并且区分函数
模型和回归模型。
问题二:在线性回归模型中,e是用bx+a预报真实值y的随机误差,
它是一个不可观测的量,那么应如何研究随机误差呢?
问题三:如何发现数据中的错误?如何衡量随机模型的拟合效果?
问题四:结合例1思考:用回归方程预报体重时应注意什么?
问题五:归纳建立回归模型的基本步骤。
问题六:若两个变量呈现非线性关系,如何解决?(分析例2)
例1 从某大学中随机选取8名女大学生,其身高和体重数据如表1-1所示.
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重.
问题一:结合例1得出线性回归模型及随机误差。并且区分函数模型和回归模型.
解:1、选取身高为自变量x,体重为因变量y,作散点图:
2.回归方程:
探究:身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
答:用这个回归方程不能给出每个身高为172cm的女大学生
的体重的预测值,只能给出她们平均体重的估计值.
由于所有的样本点不共线,而只是散布在某一直线的附近,所以身高和体重的关系可以用线性回归模型来表示:
其中a和b为模型的未知参数,e称为随机误差.
函数模型与“回归模型”的关系
函数模型:因变量y完全由自变量x确定
回归模型: 预报变量y完全由解释变量x和随机误差e确定
注:e 产生的主要原因:
(1)所用确定性函数不恰当;
(2)忽略了某些因素的影响;
(3)观测误差.
思考:产生随机误差项e的原因是什么?
问题二:在线性回归模型中,e是用bx+a预报真实值y的随机误差,
它是一个不可观测的量,那么应如何研究随机误差呢?
结合例1除了身高影响体重外的其他因素是不可测量的,不能希望有某种方法获取随机误差的值以提高预报变量的估计精度,但却可以估计预报变量观测值中所包含的随机误差,这对我们查找样本数据中的错误和模型的评价极为有用,因此在此我们引入残差概念。
e=y-(bx+a)
随机误差
e的估计量
样本点:
相应的随机误差为:
随机误差的估计值为:
称为相应于点 的残差.
问题三:如何发现数据中的错误?如何衡量随机模型的拟合效果?
(1)我们可以通过分析发现原始数据中的可疑数据,判断建立模型的拟合效果.
残差图的制作和作用:
制作:坐标纵轴为残差变量,横轴可以有不同的选择.
横轴为编号:可以考察残差与编号次序之间的关系, 常用于调查数据错误.
横轴为解释变量:可以考察残差与解释变量的关系,常用于研究模型是否有改进的余地.
作用:判断模型的适用性若模型选择的正确,残差图中的点应该分布在以横轴为中心的带形区域.
下面表格列出了女大学生身高和体重的原始数
据以及相应的残差数据.
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
残差图的制作及作用。
坐标纵轴为残差变量,横轴可以有不同的选择;
若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
对于远离横轴的点,要特别注意。
身高与体重残差图
异常点
错误数据
模型问题
几点说明:
第一个样本点和第6个样本点的残差比较大,需要确认在采集过程中是否有人为的错误.如果数据采集有错误,就予以纠正,然后再重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他的原因.
另外,残差点比较均匀地落在水平的带状区域中,说明选用的模型计较合适,这样的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高.
误差与残差,这两个概念在某程度上具有很大的相似性,
都是衡量不确定性的指标,可是两者又存在区别.
误差与测量有关,误差大小可以衡量测量的准确性,误差越大则表示测量越不准确.误差分为两类:系统误差与
随机误差.其中,系统误差与测量方案有关,通过改进测量方案可以避免系统误差.随机误差与观测者,测量工具,被观测物体的性质有关,只能尽量减小,却不能避免。
残差――与预测有关,残差大小可以衡量预测的准确性.残差越大表示预测越不准确.残差与数据本身的分布特性,回归方程的选择有关.
显然,R2的值越大,说明残差平方和越小,也就是说模型拟合效果
越好.
在线性回归模型中,R2表示解析变量对预报变量变化的贡献率.
R2越接近1,表示回归的效果越好(因为R2越接近1,表示解释变量
和预报变量的线性相关性越强).
如果某组数据可能采取几种不同回归方程进行回归分析,则可以通
过比较R2的值来做出选择,即选取R2较大的模型作为这组数据的模型.
注:相关指数R2是度量模型拟合效果的一种指标.在线性模
型中,它代表自变量刻画预报变量的能力.
(2)我们可以用相关指数R2来刻画回归的效果,其计算公式是
相关系数
相关系数的性质
(1)|r|≤1.
(2)|r|越接近于1,相关程度越强;|r|越接近于0,相关程度越弱.
问题:达到怎样程度,x、y线性相关呢?它们的相关程度怎样呢?
相关系数
r>0正相关;r<0负相关.通常:
r∈[-1,-0.75]--负相关很强;
r∈[0.75,1]—正相关很强;
r∈[-0.75,-0.3]--负相关一般; r∈[0.3, 0.75]—正相关一般;
r∈[-0.25, 0.25]--相关性较弱;
对r进行显著性检验
1
354
总计
0.36
128.361
残差变量
0.64
225.639
回归变量
比例
平方和
来源
从上中可以看出,解析变量对总效应约贡献了64%,即
R2=0.64,可以叙述为“身高解释了64%的体重变化”,而随
机误差贡献了剩余的36%.
所以,身高对体重的效应比随机误差的效应大得多.
下面我们用相关指数分析一下例1:
预报变量的变化程度
可以分解为由解释变
量引起的变化程度与
残差变量的变化程度
之和,即
;
问题四:结合例1思考:用回归方程预报体重时应注意什么?
1.回归方程只适用于我们所研究的样本的总体.
2.我们建立的回归方程一般都有时间性.
3.样本取值的范围会影响回归方程的适用范围.
4.不能期望回归方程得到的预报值就是预报变量的精确值.
涉及到统计的一些思想:
模型适用的总体;模型的时间性;
样本的取值范围对模型的影响;模型预报结果的正确理解.
一般地,建立回归模型的基本步骤为:
(1)确定研究对象,明确哪个变量是解析变量,哪个变量是预报变量.
(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系
(如是否存在线性关系等).
(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性回归方程y=bx+a).
(4)按一定规则估计回归方程中的参数(如最小二乘法).
(5)得出结果后分析残差图是否有异常(个别数据对应残差过大,或残差呈现不随机的规律性,等等),若存在异常,则检查数据是否有误,或模型是否合适等.
问题五:归纳建立回归模型的基本步骤
比《数学3》中“回归”增加的内容
数学3——统计
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题
选修1-2——统计案例
引入线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用
利用线性回归模型解决一类非线性回归问题
正确理解分析方法与结果
07广东高考题
所以预测生产100吨甲产品的成产能耗比技术改造前降低19.65吨标准煤.
1.1.1回归分析的基本思想及其初步应用
必修3(第二章 统计)知识结构
收集数据 (随机抽样)
整理、分析数据估计、推断
简单随机抽样
分层抽样
系统抽样
用样本估计总体
变量间的相关关系
用样本的频率分布估计总体分布
用样本数字特征估计总体数字特征
线性回归分析
1、两个变量的关系
不相关
相关关系
函数关系
线性相关
非线性相关
问题1:现实生活中两个变量间的关系有哪些呢?
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系.
思考:相关关系与函数关系有怎样的不同?
函数关系中的两个变量间是一种确定性关系
相关关系是一种非确定性关系
函数关系是一种理想的关系模型
相关关系在现实生活中大量存在,是更一般的情况
问题2:对于线性相关的两个变量用什么方法来刻划之间的关系呢?
2、最小二乘估计
最小二乘估计下的线性回归方程:
回归直线必过样本点的中心
3、回归分析的基本步骤:
画散点图
求回归直线方程
预报、决策
这种方法称为回归分析.
回归分析是对具有相关关系的两个变量进行统计
分析的一种常用方法.
回归分析知识结构图
问题背景分析
线性回归模型
两个变量线性相关
最小二乘法
两个变量非线性相关
非线性回归模型
残差分析
散点图
应用
注:虚线表示高中阶段不涉及的关系
教学情境设计
问题一:结合例1得出线性回归模型及随机误差。并且区分函数
模型和回归模型。
问题二:在线性回归模型中,e是用bx+a预报真实值y的随机误差,
它是一个不可观测的量,那么应如何研究随机误差呢?
问题三:如何发现数据中的错误?如何衡量随机模型的拟合效果?
问题四:结合例1思考:用回归方程预报体重时应注意什么?
问题五:归纳建立回归模型的基本步骤。
问题六:若两个变量呈现非线性关系,如何解决?(分析例2)
例1 从某大学中随机选取8名女大学生,其身高和体重数据如表1-1所示.
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重.
问题一:结合例1得出线性回归模型及随机误差。并且区分函数模型和回归模型.
解:1、选取身高为自变量x,体重为因变量y,作散点图:
2.回归方程:
探究:身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
答:用这个回归方程不能给出每个身高为172cm的女大学生
的体重的预测值,只能给出她们平均体重的估计值.
由于所有的样本点不共线,而只是散布在某一直线的附近,所以身高和体重的关系可以用线性回归模型来表示:
其中a和b为模型的未知参数,e称为随机误差.
函数模型与“回归模型”的关系
函数模型:因变量y完全由自变量x确定
回归模型: 预报变量y完全由解释变量x和随机误差e确定
注:e 产生的主要原因:
(1)所用确定性函数不恰当;
(2)忽略了某些因素的影响;
(3)观测误差.
思考:产生随机误差项e的原因是什么?
问题二:在线性回归模型中,e是用bx+a预报真实值y的随机误差,
它是一个不可观测的量,那么应如何研究随机误差呢?
结合例1除了身高影响体重外的其他因素是不可测量的,不能希望有某种方法获取随机误差的值以提高预报变量的估计精度,但却可以估计预报变量观测值中所包含的随机误差,这对我们查找样本数据中的错误和模型的评价极为有用,因此在此我们引入残差概念。
e=y-(bx+a)
随机误差
e的估计量
样本点:
相应的随机误差为:
随机误差的估计值为:
称为相应于点 的残差.
问题三:如何发现数据中的错误?如何衡量随机模型的拟合效果?
(1)我们可以通过分析发现原始数据中的可疑数据,判断建立模型的拟合效果.
残差图的制作和作用:
制作:坐标纵轴为残差变量,横轴可以有不同的选择.
横轴为编号:可以考察残差与编号次序之间的关系, 常用于调查数据错误.
横轴为解释变量:可以考察残差与解释变量的关系,常用于研究模型是否有改进的余地.
作用:判断模型的适用性若模型选择的正确,残差图中的点应该分布在以横轴为中心的带形区域.
下面表格列出了女大学生身高和体重的原始数
据以及相应的残差数据.
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
残差图的制作及作用。
坐标纵轴为残差变量,横轴可以有不同的选择;
若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
对于远离横轴的点,要特别注意。
身高与体重残差图
异常点
错误数据
模型问题
几点说明:
第一个样本点和第6个样本点的残差比较大,需要确认在采集过程中是否有人为的错误.如果数据采集有错误,就予以纠正,然后再重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他的原因.
另外,残差点比较均匀地落在水平的带状区域中,说明选用的模型计较合适,这样的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高.
误差与残差,这两个概念在某程度上具有很大的相似性,
都是衡量不确定性的指标,可是两者又存在区别.
误差与测量有关,误差大小可以衡量测量的准确性,误差越大则表示测量越不准确.误差分为两类:系统误差与
随机误差.其中,系统误差与测量方案有关,通过改进测量方案可以避免系统误差.随机误差与观测者,测量工具,被观测物体的性质有关,只能尽量减小,却不能避免。
残差――与预测有关,残差大小可以衡量预测的准确性.残差越大表示预测越不准确.残差与数据本身的分布特性,回归方程的选择有关.
显然,R2的值越大,说明残差平方和越小,也就是说模型拟合效果
越好.
在线性回归模型中,R2表示解析变量对预报变量变化的贡献率.
R2越接近1,表示回归的效果越好(因为R2越接近1,表示解释变量
和预报变量的线性相关性越强).
如果某组数据可能采取几种不同回归方程进行回归分析,则可以通
过比较R2的值来做出选择,即选取R2较大的模型作为这组数据的模型.
注:相关指数R2是度量模型拟合效果的一种指标.在线性模
型中,它代表自变量刻画预报变量的能力.
(2)我们可以用相关指数R2来刻画回归的效果,其计算公式是
相关系数
相关系数的性质
(1)|r|≤1.
(2)|r|越接近于1,相关程度越强;|r|越接近于0,相关程度越弱.
问题:达到怎样程度,x、y线性相关呢?它们的相关程度怎样呢?
相关系数
r>0正相关;r<0负相关.通常:
r∈[-1,-0.75]--负相关很强;
r∈[0.75,1]—正相关很强;
r∈[-0.75,-0.3]--负相关一般; r∈[0.3, 0.75]—正相关一般;
r∈[-0.25, 0.25]--相关性较弱;
对r进行显著性检验
1
354
总计
0.36
128.361
残差变量
0.64
225.639
回归变量
比例
平方和
来源
从上中可以看出,解析变量对总效应约贡献了64%,即
R2=0.64,可以叙述为“身高解释了64%的体重变化”,而随
机误差贡献了剩余的36%.
所以,身高对体重的效应比随机误差的效应大得多.
下面我们用相关指数分析一下例1:
预报变量的变化程度
可以分解为由解释变
量引起的变化程度与
残差变量的变化程度
之和,即
;
问题四:结合例1思考:用回归方程预报体重时应注意什么?
1.回归方程只适用于我们所研究的样本的总体.
2.我们建立的回归方程一般都有时间性.
3.样本取值的范围会影响回归方程的适用范围.
4.不能期望回归方程得到的预报值就是预报变量的精确值.
涉及到统计的一些思想:
模型适用的总体;模型的时间性;
样本的取值范围对模型的影响;模型预报结果的正确理解.
一般地,建立回归模型的基本步骤为:
(1)确定研究对象,明确哪个变量是解析变量,哪个变量是预报变量.
(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系
(如是否存在线性关系等).
(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性回归方程y=bx+a).
(4)按一定规则估计回归方程中的参数(如最小二乘法).
(5)得出结果后分析残差图是否有异常(个别数据对应残差过大,或残差呈现不随机的规律性,等等),若存在异常,则检查数据是否有误,或模型是否合适等.
问题五:归纳建立回归模型的基本步骤
比《数学3》中“回归”增加的内容
数学3——统计
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题
选修1-2——统计案例
引入线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用
利用线性回归模型解决一类非线性回归问题
正确理解分析方法与结果
07广东高考题
所以预测生产100吨甲产品的成产能耗比技术改造前降低19.65吨标准煤.
