五年级下册数学课件-3.4 长方体和正方体的体积西师大版 (34张PPT)
文档属性
| 名称 | 五年级下册数学课件-3.4 长方体和正方体的体积西师大版 (34张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 234.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 07:11:50 | ||
图片预览






文档简介
(共34张PPT)
长方体和正方体的体积(例1)
1、什么叫做物体的体积呢?
每个物体都占有一定的空间,我们把“物体所占空间的大小,叫做物体的体积”.
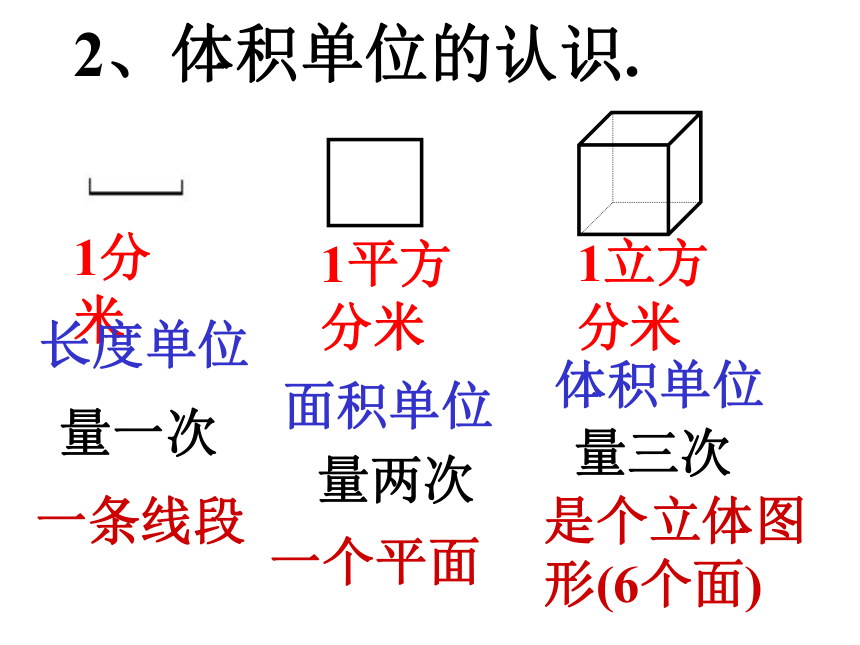
2、体积单位的认识.
1分米
长度单位
1平方分米
面积单位
1立方分米
体积单位
量一次
量两次
量三次
一条线段
一个平面
是个立体图形(6个面)
填空:
(1)一块橡皮擦的体积约是8(
);
用多么大的体积单位表示下面物体的体积比较适当?
(2)一台录音机的体积约是20(
);
立方厘米
立方分米
填空:
用多么大的体积单位表示下面物体的体积比较适当?
(3)运货集装箱的体积约是40(
);
(4)常用的公制体积单位有:立方(
);立方(
);立方(
)
.
立方米
厘米
分米
米
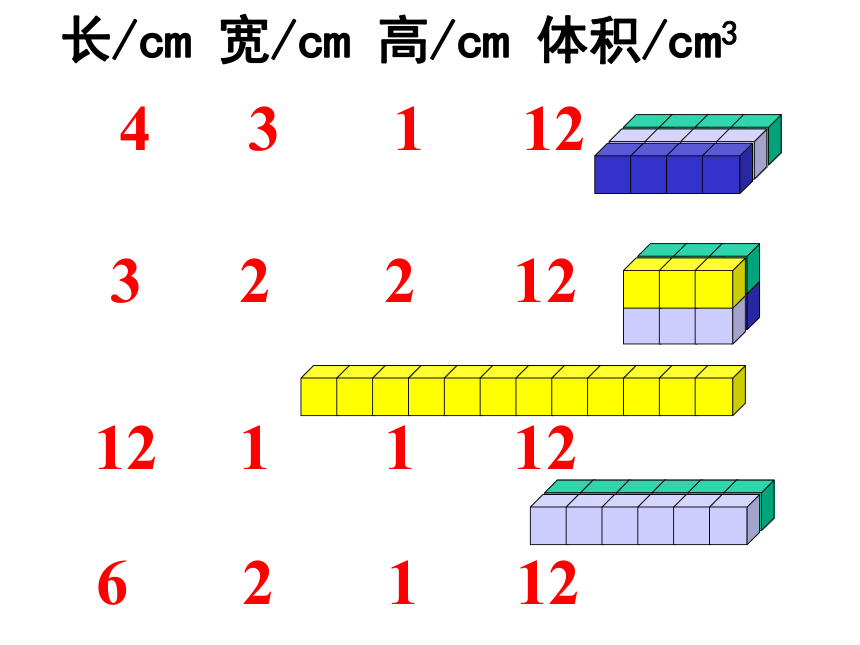
长/cm
宽/cm
高/cm
体积/cm3
4
3
1
12
3
2
2
12
12
1
1
12
6
2
1
12
1、这些长方体有什么共同点?不同点?
体积都相同,而长、宽、高不同。
2、为什么这些长方体的长、宽、高不同,即形状不同而体积相同呢?
因为它们都含有同样多的体积单位------12个1厘米3
P53
例1
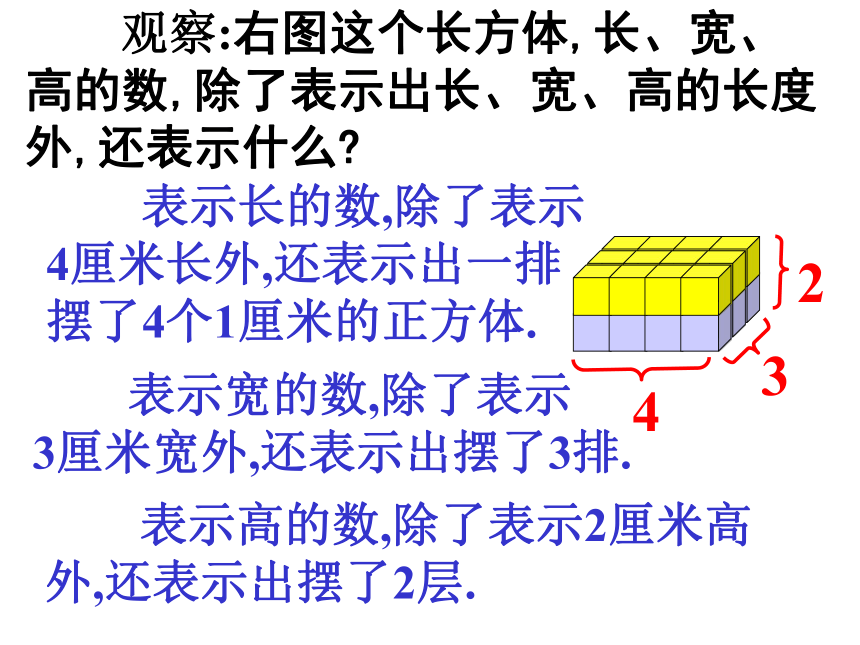
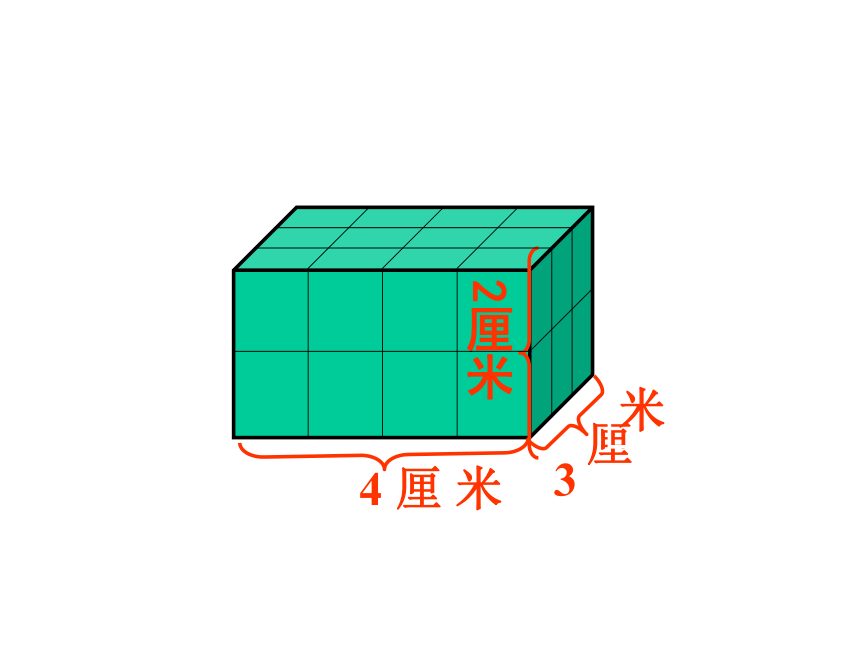
观察:右图这个长方体,长、宽、高的数,除了表示出长、宽、高的长度外,还表示什么?
表示长的数,除了表示4厘米长外,还表示出一排摆了4个1厘米的正方体.
4
3
2
表示宽的数,除了表示
3厘米宽外,还表示出摆了3排.
表示高的数,除了表示2厘米高外,还表示出摆了2层.
4
3
2
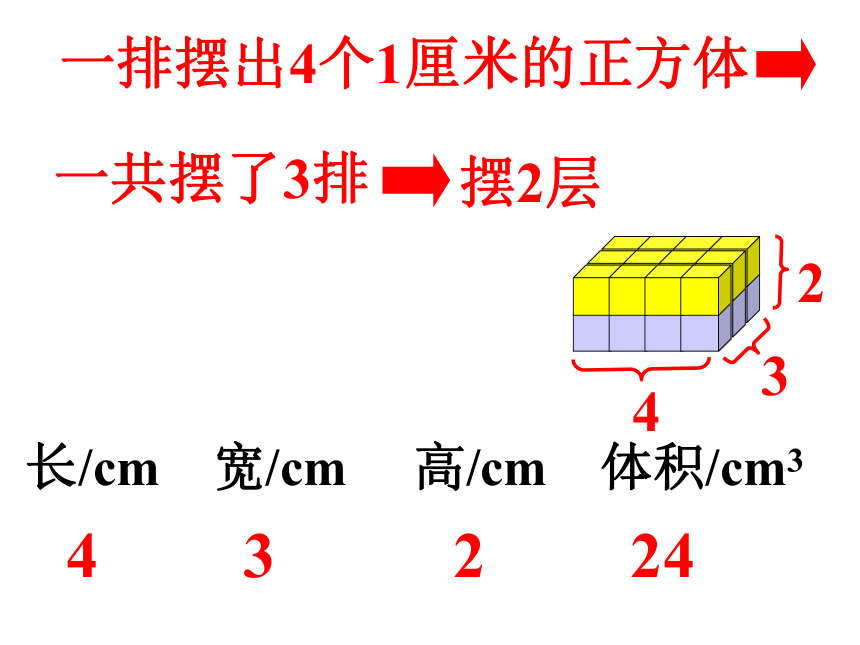
一排摆出4个1厘米的正方体
一共摆了3排
摆2层
长/cm
宽/cm
高/cm
体积/cm3
4
3
2
24
4
厘
米
2厘米
3
厘
米
2
厘
米
4
厘
米
3
厘
米
24立方厘米
4
厘
米
3
米
厘
2厘米
24立方厘米
3
米
厘
4
厘
米
1厘米
12立方厘米
想一想:如果要摆一个长5厘米,宽4厘米,高3厘米的长方体,该如何摆?体积是多少?
5
4
3
一排摆5个一共摆4排上下摆3层
这些数据与长方体的体积有没有关系?是什麽关系?
12
24
=
×
×
=
×
×
每排数
排数
层数
4
4
1
2
3
3
体积
=
×
×
4
厘
米
3
米
厘
3厘米
36立方厘米
4
厘
米
3
米
厘
4厘米
48立方厘米
4
厘
米
3
米
厘
60立方厘米
5厘米
12
24
=
×
×
=
×
×
每排数
排数
层数
4
4
1
2
3
3
体积
=
×
×
36
4
3
3
48
4
3
4
=
=
×
×
×
×
长
宽
高
4
3
60
5
=
×
×
12
24
=
×
×
=
×
×
每排数
排数
层数
4
4
1
2
3
3
体积
=
×
×
36
4
3
3
48
4
3
4
=
=
×
×
×
×
长
宽
高
4
3
60
5
=
×
×
5
4
3
长方体所含体积单位的个数正好等于它的长、宽、高的乘积.
即:长方体的体积=长×宽×高
V=abh
例:一个长方体,长7厘米,宽4厘米,高3厘米,它的体积是多少?
7×4×3=84(cm3
)
答:它的体积是84cm.
7cm
4cm
3cm
练习:一块水泥板,长5分米,宽3分米,厚2分米,这块水泥板的体积是多少分米3
?
5
3
2
5×3×2=30(分米3
)
答:这块水泥板的体积是30立方分米.
长5厘米
宽4厘米
高3厘米
长5厘米,宽4厘米,高3厘
米的长方体,长缩
短1厘米(图上从
右边去掉一排),
高增加1厘米(图上在上边增加一排),此时的长、宽、高各是多少?变成了什麽图形?
长4厘米
宽4厘米
高4厘米
长4厘米,宽4厘米,高4厘米;变成了正方体.
因为正方体是长、宽、高都相等的长方体,所以
这个正方体的体积是4×4×4=64(立方厘米)
棱长4厘米
棱长4厘米
棱长4厘米
正方体的体积=棱长×棱长×棱长
V=a.a.a
V=a3
例:光明纸盒厂生产一种正方形纸板箱,棱长是5分米,体积是多少立方分米?
53
=5×5×5=125(立方分米)
答:体积是125立方分米。
填空:
长方体的体积=(
)×(
)
×(
);正方体的(
)=(
)=(
),所以正方体的体积=(
)
×(
)
×(
)。
因为,长方体所含体积单位的个数正好等于长、宽、高的乘积,所以长方体的体积=(
)×(
)×(
),用字母表示就是
(
).
(2).因为正方体的(
)都
相等,所以正方体的体积
=( )×( )×( ),
用字母表示为(
),
a
读作(
),表
示(
)。
3
计算下面正方体的体积
4
厘米
9
分
米
4×4×4=64(立方厘米)
9×9×9=729(立方分米)
这节课我们学习了什麽?懂得了什么?
想到了吗?
长方体和正方体的体积(例1)
1、什么叫做物体的体积呢?
每个物体都占有一定的空间,我们把“物体所占空间的大小,叫做物体的体积”.
2、体积单位的认识.
1分米
长度单位
1平方分米
面积单位
1立方分米
体积单位
量一次
量两次
量三次
一条线段
一个平面
是个立体图形(6个面)
填空:
(1)一块橡皮擦的体积约是8(
);
用多么大的体积单位表示下面物体的体积比较适当?
(2)一台录音机的体积约是20(
);
立方厘米
立方分米
填空:
用多么大的体积单位表示下面物体的体积比较适当?
(3)运货集装箱的体积约是40(
);
(4)常用的公制体积单位有:立方(
);立方(
);立方(
)
.
立方米
厘米
分米
米
长/cm
宽/cm
高/cm
体积/cm3
4
3
1
12
3
2
2
12
12
1
1
12
6
2
1
12
1、这些长方体有什么共同点?不同点?
体积都相同,而长、宽、高不同。
2、为什么这些长方体的长、宽、高不同,即形状不同而体积相同呢?
因为它们都含有同样多的体积单位------12个1厘米3
P53
例1
观察:右图这个长方体,长、宽、高的数,除了表示出长、宽、高的长度外,还表示什么?
表示长的数,除了表示4厘米长外,还表示出一排摆了4个1厘米的正方体.
4
3
2
表示宽的数,除了表示
3厘米宽外,还表示出摆了3排.
表示高的数,除了表示2厘米高外,还表示出摆了2层.
4
3
2
一排摆出4个1厘米的正方体
一共摆了3排
摆2层
长/cm
宽/cm
高/cm
体积/cm3
4
3
2
24
4
厘
米
2厘米
3
厘
米
2
厘
米
4
厘
米
3
厘
米
24立方厘米
4
厘
米
3
米
厘
2厘米
24立方厘米
3
米
厘
4
厘
米
1厘米
12立方厘米
想一想:如果要摆一个长5厘米,宽4厘米,高3厘米的长方体,该如何摆?体积是多少?
5
4
3
一排摆5个一共摆4排上下摆3层
这些数据与长方体的体积有没有关系?是什麽关系?
12
24
=
×
×
=
×
×
每排数
排数
层数
4
4
1
2
3
3
体积
=
×
×
4
厘
米
3
米
厘
3厘米
36立方厘米
4
厘
米
3
米
厘
4厘米
48立方厘米
4
厘
米
3
米
厘
60立方厘米
5厘米
12
24
=
×
×
=
×
×
每排数
排数
层数
4
4
1
2
3
3
体积
=
×
×
36
4
3
3
48
4
3
4
=
=
×
×
×
×
长
宽
高
4
3
60
5
=
×
×
12
24
=
×
×
=
×
×
每排数
排数
层数
4
4
1
2
3
3
体积
=
×
×
36
4
3
3
48
4
3
4
=
=
×
×
×
×
长
宽
高
4
3
60
5
=
×
×
5
4
3
长方体所含体积单位的个数正好等于它的长、宽、高的乘积.
即:长方体的体积=长×宽×高
V=abh
例:一个长方体,长7厘米,宽4厘米,高3厘米,它的体积是多少?
7×4×3=84(cm3
)
答:它的体积是84cm.
7cm
4cm
3cm
练习:一块水泥板,长5分米,宽3分米,厚2分米,这块水泥板的体积是多少分米3
?
5
3
2
5×3×2=30(分米3
)
答:这块水泥板的体积是30立方分米.
长5厘米
宽4厘米
高3厘米
长5厘米,宽4厘米,高3厘
米的长方体,长缩
短1厘米(图上从
右边去掉一排),
高增加1厘米(图上在上边增加一排),此时的长、宽、高各是多少?变成了什麽图形?
长4厘米
宽4厘米
高4厘米
长4厘米,宽4厘米,高4厘米;变成了正方体.
因为正方体是长、宽、高都相等的长方体,所以
这个正方体的体积是4×4×4=64(立方厘米)
棱长4厘米
棱长4厘米
棱长4厘米
正方体的体积=棱长×棱长×棱长
V=a.a.a
V=a3
例:光明纸盒厂生产一种正方形纸板箱,棱长是5分米,体积是多少立方分米?
53
=5×5×5=125(立方分米)
答:体积是125立方分米。
填空:
长方体的体积=(
)×(
)
×(
);正方体的(
)=(
)=(
),所以正方体的体积=(
)
×(
)
×(
)。
因为,长方体所含体积单位的个数正好等于长、宽、高的乘积,所以长方体的体积=(
)×(
)×(
),用字母表示就是
(
).
(2).因为正方体的(
)都
相等,所以正方体的体积
=( )×( )×( ),
用字母表示为(
),
a
读作(
),表
示(
)。
3
计算下面正方体的体积
4
厘米
9
分
米
4×4×4=64(立方厘米)
9×9×9=729(立方分米)
这节课我们学习了什麽?懂得了什么?
想到了吗?
