勾股定理第一课时教案
图片预览
文档简介
勾股定理第一课时
教学目标:
知识目标:
1、了解多种拼图方法,验证勾股定理,感受解决同一个问题方法的多样性。
2、通过实例进一步了解勾股定理,应用勾股定理进行简单的计算和证明。,
数学思考:在拼图变换以及实际操作过程中让学生进一步体会数形结合的思想以及数学知识之间内在联系。
情感态度:让学生经历观察操作探究归纳总结等过程,获得勾股定理。能够运用勾股定理解决实际问题。
教学重点:通过自主学习验证归纳勾股定理的内容及证明,并进行应用。
教学难点:勾股定理的证明。
教学过程:
一、课前准备:
1、每位同学准备四个全等的直角三角形。
2、查阅资料,网络搜索有关勾股定理的知识。
3、自主阅读课本本节内容。
二、探究新知:
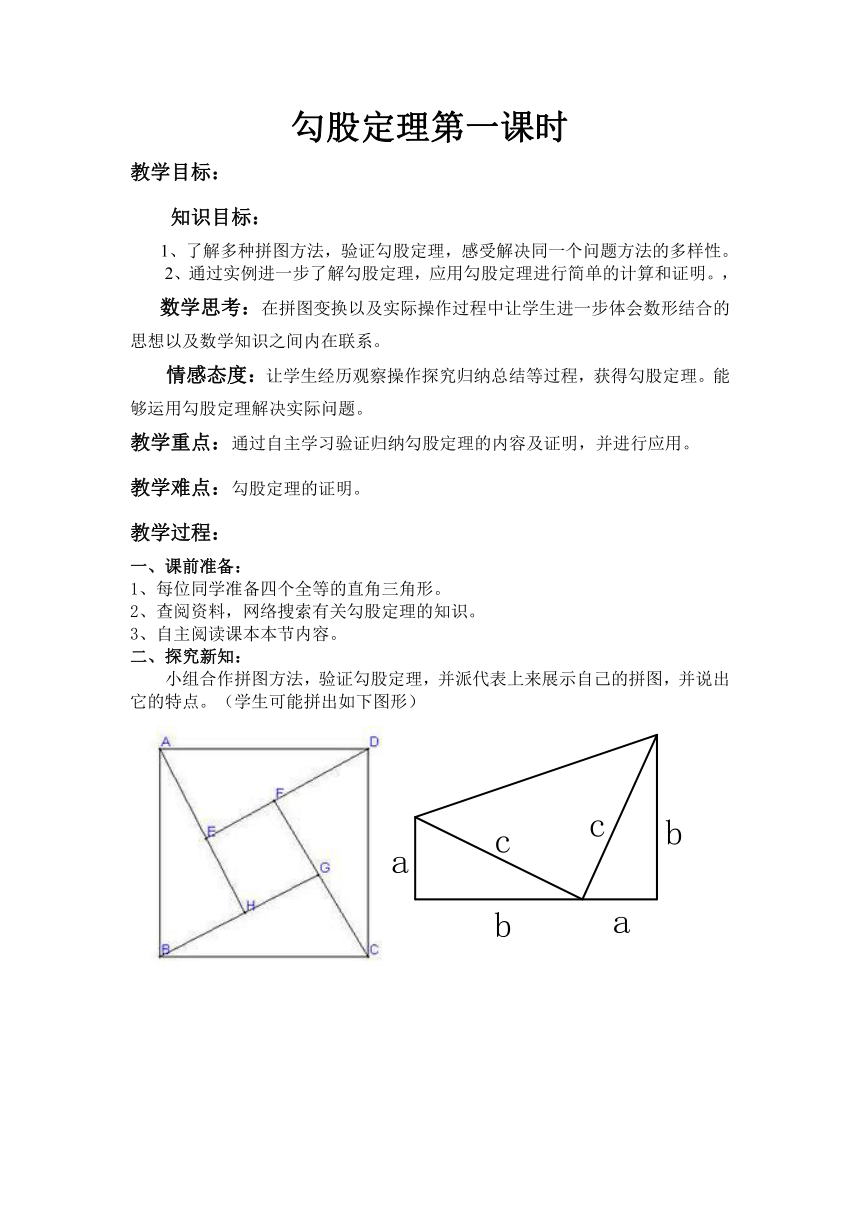
小组合作拼图方法,验证勾股定理,并派代表上来展示自己的拼图,并说出它的特点。(学生可能拼出如下图形)
从你所拼的图形的面积构造等式验证勾股定理
看是否能得出 :c2=a2+b2
每一小组选一种图形写出验证的过程,小组间进行交流。
归纳定理:
① 用语言表达勾股定理
② 用式子表达勾股定理
③ 运用勾股定理时该注意些什么
介绍勾股定理的历史:我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五。”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5。这就是雏形的勾股定理。这个古老的精彩的证法,出自我国古代数学家之手。激发学生的民族自豪感,和爱国情怀。
例习题分析:
例:已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
求证:a2+b2=c2。
分析:
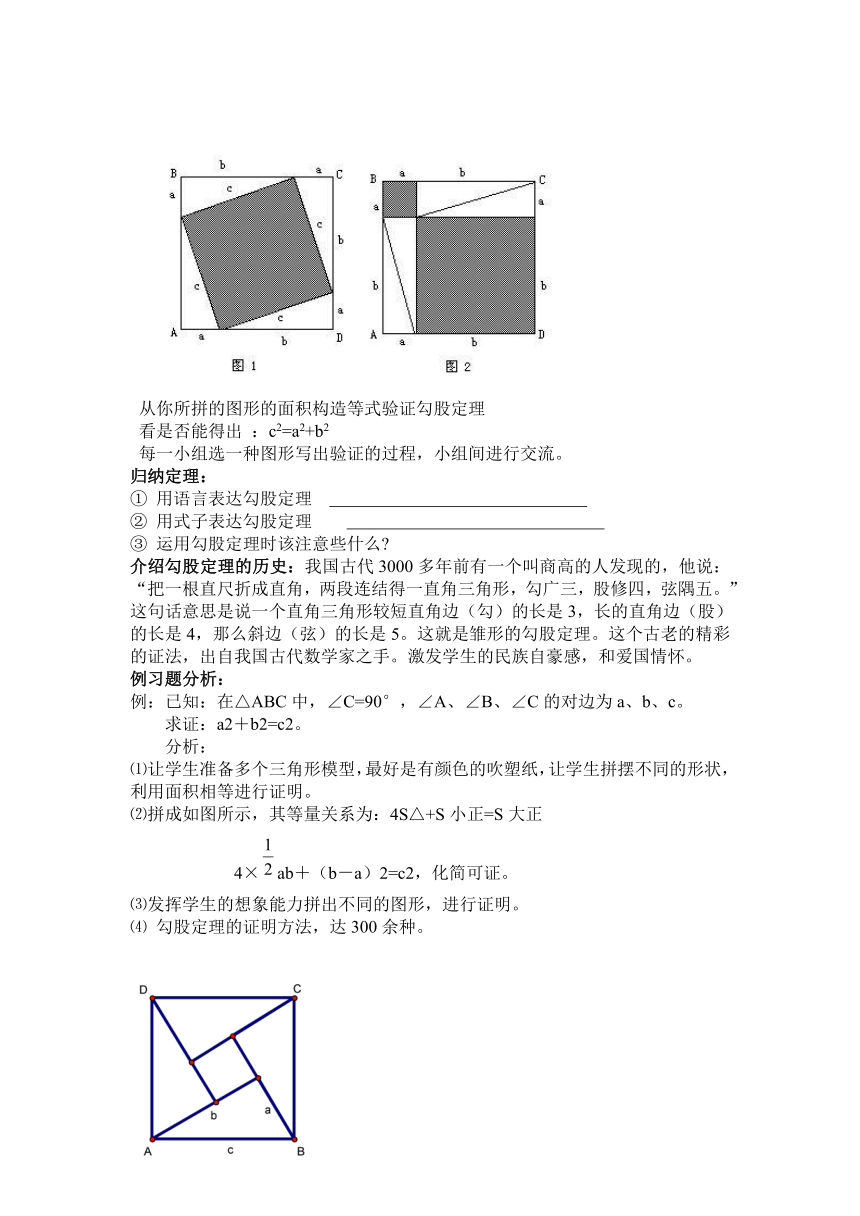
⑴让学生准备多个三角形模型,最好是有颜色的吹塑纸,让学生拼摆不同的形状,利用面积相等进行证明。
⑵拼成如图所示,其等量关系为:4S△+S小正=S大正
4×ab+(b-a)2=c2,化简可证。
⑶发挥学生的想象能力拼出不同的图形,进行证明。
⑷ 勾股定理的证明方法,达300余种。
三、课堂练习
1.勾股定理的具体内容是: 。
2.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
⑴两锐角之间的关系: ;
⑵若D为斜边中点,则斜边中线 ;
⑶若∠B=30°,则∠B的对边和斜边: ;
⑷三边之间的关系: 。
3.△ABC的三边a、b、c,若满足b2= a2+c2,则 =90°; 若满足b2>c2+a2,则∠B是 角; 若满足b2<c2+a2,则∠B是 角 。
4.根据如图所示,利用面积法证明勾股定理。
四、课内总结
我们通过什么方法来推导勾股定理的?拼图法证明勾股定理用了什么数学思想?勾股定理可以用来解决那些问题?
五、布置作业
1、如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
提示:
① AD 与BD有何关系?
② 设CD=x,则AD=
③ 在△ACD中根据勾股定理可列出
构造方程来解。
2、下列各图中所示的线段的长度或正方形的面积为多少。(注:下列各图中的三角形均为直角三角形)
教学目标:
知识目标:
1、了解多种拼图方法,验证勾股定理,感受解决同一个问题方法的多样性。
2、通过实例进一步了解勾股定理,应用勾股定理进行简单的计算和证明。,
数学思考:在拼图变换以及实际操作过程中让学生进一步体会数形结合的思想以及数学知识之间内在联系。
情感态度:让学生经历观察操作探究归纳总结等过程,获得勾股定理。能够运用勾股定理解决实际问题。
教学重点:通过自主学习验证归纳勾股定理的内容及证明,并进行应用。
教学难点:勾股定理的证明。
教学过程:
一、课前准备:
1、每位同学准备四个全等的直角三角形。
2、查阅资料,网络搜索有关勾股定理的知识。
3、自主阅读课本本节内容。
二、探究新知:
小组合作拼图方法,验证勾股定理,并派代表上来展示自己的拼图,并说出它的特点。(学生可能拼出如下图形)
从你所拼的图形的面积构造等式验证勾股定理
看是否能得出 :c2=a2+b2
每一小组选一种图形写出验证的过程,小组间进行交流。
归纳定理:
① 用语言表达勾股定理
② 用式子表达勾股定理
③ 运用勾股定理时该注意些什么
介绍勾股定理的历史:我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五。”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5。这就是雏形的勾股定理。这个古老的精彩的证法,出自我国古代数学家之手。激发学生的民族自豪感,和爱国情怀。
例习题分析:
例:已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
求证:a2+b2=c2。
分析:
⑴让学生准备多个三角形模型,最好是有颜色的吹塑纸,让学生拼摆不同的形状,利用面积相等进行证明。
⑵拼成如图所示,其等量关系为:4S△+S小正=S大正
4×ab+(b-a)2=c2,化简可证。
⑶发挥学生的想象能力拼出不同的图形,进行证明。
⑷ 勾股定理的证明方法,达300余种。
三、课堂练习
1.勾股定理的具体内容是: 。
2.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
⑴两锐角之间的关系: ;
⑵若D为斜边中点,则斜边中线 ;
⑶若∠B=30°,则∠B的对边和斜边: ;
⑷三边之间的关系: 。
3.△ABC的三边a、b、c,若满足b2= a2+c2,则 =90°; 若满足b2>c2+a2,则∠B是 角; 若满足b2<c2+a2,则∠B是 角 。
4.根据如图所示,利用面积法证明勾股定理。
四、课内总结
我们通过什么方法来推导勾股定理的?拼图法证明勾股定理用了什么数学思想?勾股定理可以用来解决那些问题?
五、布置作业
1、如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
提示:
① AD 与BD有何关系?
② 设CD=x,则AD=
③ 在△ACD中根据勾股定理可列出
构造方程来解。
2、下列各图中所示的线段的长度或正方形的面积为多少。(注:下列各图中的三角形均为直角三角形)
