人教版七年级下册7.2坐标方法的简单应用课后练习试卷(Word版含答案)
文档属性
| 名称 | 人教版七年级下册7.2坐标方法的简单应用课后练习试卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 190.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 00:00:00 | ||
图片预览



文档简介
人教版七年级下册7.2《坐标方法的简单应用》课后练习
一.选择题
1.在平面直角坐标系中,将点P(﹣3,2)向左平移2个单位长度后得到的点的坐标为( )
A.(﹣5,2) B.(﹣3,﹣1) C.(﹣3,4) D.(﹣1,2)
2.下列说法正确的是( )
A.若点A(3,﹣1),则点A到x轴的距离为3
B.平行于y轴的直线上所有点的纵坐标都相同
C.(﹣2,2)与(2,﹣2)表示两个不同的点
D.若点Q(a,b)在x轴上,则a=0
3.如图所示的象棋盘上,若“帅”位于点(1,﹣2)上,“相”位于点(3,﹣2)上,则“炮”位于点( )
A.(﹣2,1) B.(﹣1,2) C.(﹣1,1) D.(﹣2,2)
4.在平面直角坐标系中,将点P(﹣1,0)向右平移2个单位,再向上平移2个单位,得到点P′,则点P′在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知点A(0,﹣6),点B(0,3),则A,B两点间的距离是( )
A.﹣9 B.9 C.﹣3 D.3
6.在平面直角坐标系中,点A的坐标为(﹣4,3),AB∥y轴,AB=5,则点B的坐标为( )
A.(1,3) B.(﹣4,8)
C.(﹣4,8)或(﹣4,﹣2) D.(1,3)或(﹣9,3)
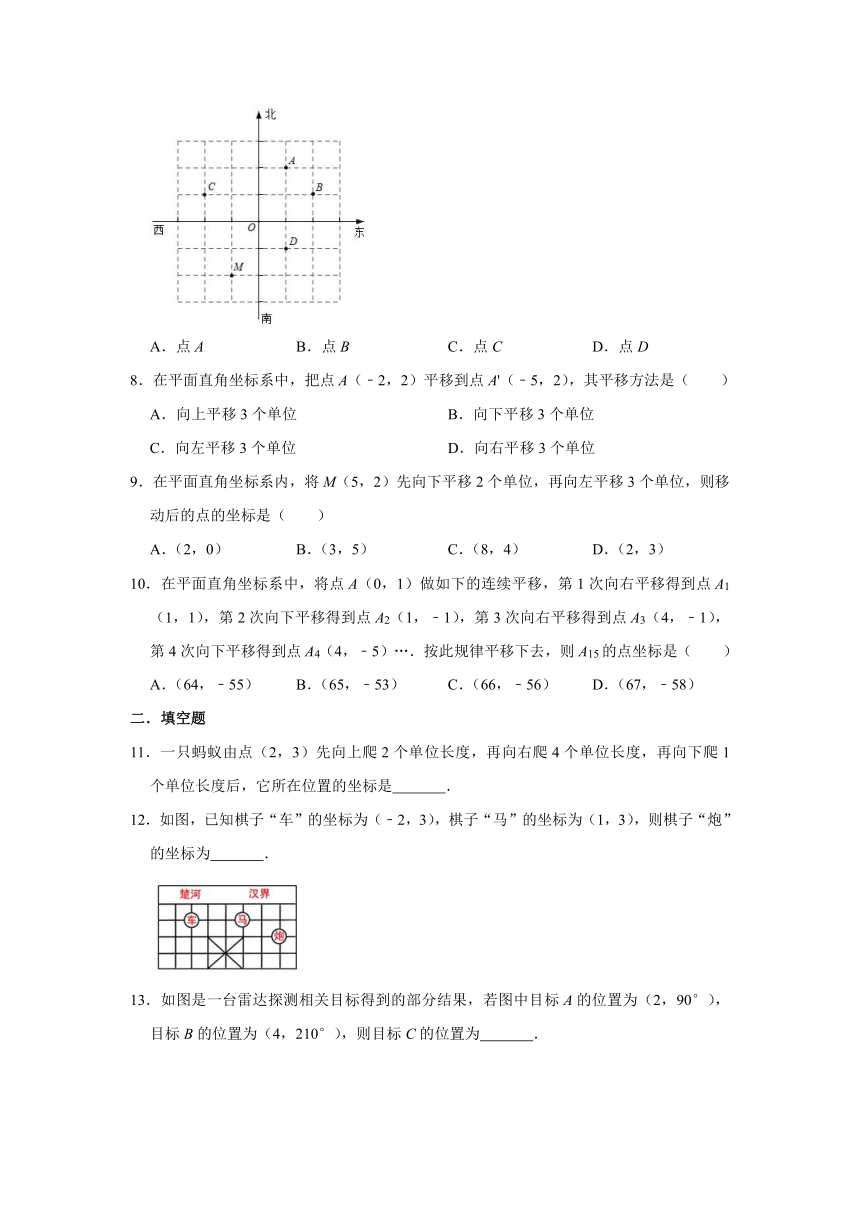
7.已知小明从点O出发,先向西走10米,再向南走20米,到达点M,如果点M的位置用(﹣10,﹣20)表示,那么(10,﹣10)表示的位置是( )
A.点A B.点B C.点C D.点D
8.在平面直角坐标系中,把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是( )
A.向上平移3个单位 B.向下平移3个单位
C.向左平移3个单位 D.向右平移3个单位
9.在平面直角坐标系内,将M(5,2)先向下平移2个单位,再向左平移3个单位,则移动后的点的坐标是( )
A.(2,0) B.(3,5) C.(8,4) D.(2,3)
10.在平面直角坐标系中,将点A(0,1)做如下的连续平移,第1次向右平移得到点A1(1,1),第2次向下平移得到点A2(1,﹣1),第3次向右平移得到点A3(4,﹣1),第4次向下平移得到点A4(4,﹣5)….按此规律平移下去,则A15的点坐标是( )
A.(64,﹣55) B.(65,﹣53) C.(66,﹣56) D.(67,﹣58)
二.填空题
11.一只蚂蚁由点(2,3)先向上爬2个单位长度,再向右爬4个单位长度,再向下爬1个单位长度后,它所在位置的坐标是 .
12.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为 .
13.如图是一台雷达探测相关目标得到的部分结果,若图中目标A的位置为(2,90°),目标B的位置为(4,210°),则目标C的位置为 .
14.若点P(2﹣m,﹣1),将P点向右平移2个单位长度后落在y轴上,则m= .
15.如图,点A、B分别在x轴和y轴上,OA=1,OB=2,若将线段AB平移至A'B',则a+b的值为 .
16.在平面直角坐标系中,若点M(2,4)与点N(x,4)之间的距离是3,则x的值是 .
三.解答题
17.如图所示的是某市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度),若海洋极地公园的坐标为(4,0),大唐芙蓉园的坐标为(2,﹣1),请建立平面直角坐标系,并用坐标表示大明宫国家遗址公园的位置.
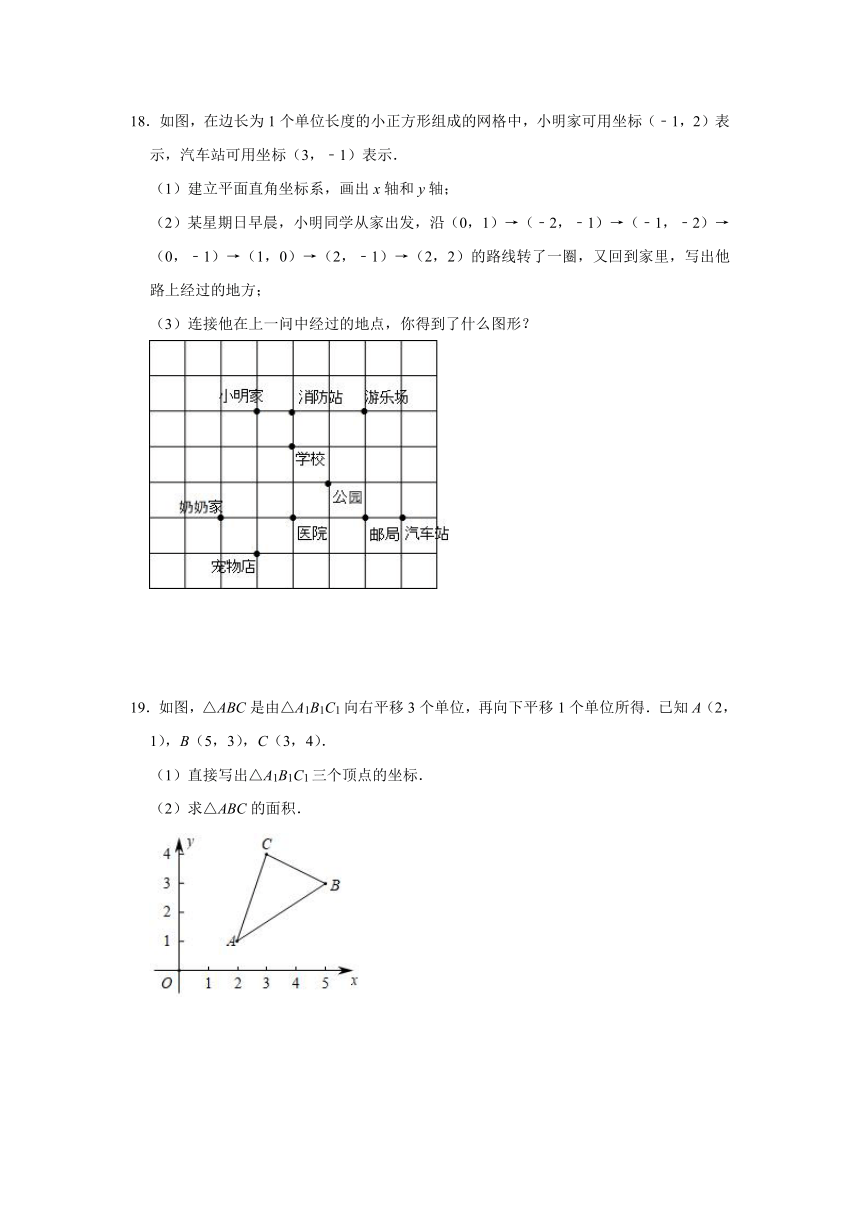
18.如图,在边长为1个单位长度的小正方形组成的网格中,小明家可用坐标(﹣1,2)表示,汽车站可用坐标(3,﹣1)表示.
(1)建立平面直角坐标系,画出x轴和y轴;
(2)某星期日早晨,小明同学从家出发,沿(0,1)→(﹣2,﹣1)→(﹣1,﹣2)→(0,﹣1)→(1,0)→(2,﹣1)→(2,2)的路线转了一圈,又回到家里,写出他路上经过的地方;
(3)连接他在上一问中经过的地点,你得到了什么图形?
19.如图,△ABC是由△A1B1C1向右平移3个单位,再向下平移1个单位所得.已知A(2,1),B(5,3),C(3,4).
(1)直接写出△A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
20.已知坐标平面内的三个点A(1,3)、B(3,1)、O(0,0).
(1)求△ABO的面积;
(2)平移△ABO至△A1B1O1,当点A1和点B重合时,点O1的坐标是 ;
(3)平移△ABO至△A2B2O2,需要至少向下平移超过 单位,并且至少向左平移 个单位,才能使△A2B2O2位于第三象限.
21.已知,点P(2m﹣6,m+2).
(1)若点P在y轴上,P点的坐标为 ;
(2)若点P的纵坐标比横坐标大6,求点P在第几象限?
(3)若点P和点Q都在过A(2,3)点且与x轴平行的直线上,AQ=3,求Q点的坐标.
22.按要求画图及填空:
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
(1)点A的坐标为 ;
(2)将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1,画出△A1B1C1.
(3)△A1B1C1的面积为 .
参考答案
一.选择题
1.解:将点P(﹣3,2)向左平移2个单位长度得到的点坐标为(﹣3﹣2,2),即(﹣5,2),
选:A.
2.解:A、若点A(3,﹣1),则点A到x轴的距离应该是1,本选项错误,不符合题意.
B、平行于y轴的直线上所有点的纵坐标都相同,错误,应该是横坐标相同,本选项不符合题意.
C、(﹣2,2)与(2,﹣2)表示两个不同的点,正确,本选项符合题意.
D、若点Q(a,b)在x轴上,应该是b=0,本选项错误,不符合题意.
选:C.
3.解:如图所示:则“炮”位于点(﹣2,1).
选:A.
4.解:由题意,P′(﹣1+2,0+2),即P′(1,2),在第一象限,
选:A.
5.解:∵A(0,﹣6),点B(0,3),
∴A,B两点间的距离=3﹣(﹣6)=9.
选:B.
6.解:∵AB∥y轴,
∴A、B两点的横坐标相同,
又AB=5,
∴B点纵坐标为:3+5=8或3﹣5=﹣2,
∴B点的坐标为:(﹣4,﹣2)或(﹣4,8);
选:C.
7.解:∵点M的位置用(﹣10,﹣20)表示,
∴(10,﹣10)表示D点.
选:D.
8.解:把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是向左平移3个单位,
选:C.
9.解:平移后的坐标为(5﹣3,2﹣2),即坐标为(2,0),
选:A.
10.解:由题意,可知点A第15次平移至点A15的横坐标是0+1+3+5+7+9+11+13+15=64,纵坐标是1﹣2﹣4﹣6﹣8﹣10﹣12﹣14=﹣55,
即点A15的坐标是(64,﹣55).
选:A.
二.填空题
11.解:点(2,3)先向上爬2个单位长度,所得点的坐标为(2,5),
再向右爬4个单位长度,所得点的坐标为(6,5),
再向下爬1个单位长度后,所得点的坐标为(6,4),
答案为:(6,4).
12.解:∵棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3)
∴坐标系的原点为O,如图所示,
∴棋子“炮”的坐标为(3,2).答案填:(3,2).
13.解:由题意,点C的位置为(3,150°).
答案为(3,150°).
14.解:点P(2﹣m,﹣1),将P点向右平移2个单位长度后点的坐标为(4﹣m,﹣1),
∵向右平移2个单位长度后落在y轴上,
∴4﹣m=0,
解得:m=4,
答案为:4.
15.解:由作图可知,线段AB向右平移3个单位,再向下平移1个单位得到线段A′B′,
∵A(﹣1,0),B(0,2),
∴A′(2,﹣1),B′(3,1),
∴a=﹣1,b=3,
∴a+b=2,
答案为:2.
16.解:∵点M(2,4)与点N(x,4)之间的距离是3,
∴|2﹣x|=3,
解得,x=﹣1或x=5,
答案为:﹣1或5.
三.解答题
17.解:如图所示:
大明宫国家遗址公园(1,5).
18.解:(1)如图,建立平面直角坐标系;
(2)小明家﹣学校﹣奶奶家﹣宠物店﹣医院﹣公园﹣邮局﹣游乐场﹣消防站﹣小明家;
(3)连接他在上一问中经过的地点,得到“箭头”状的图形.
19.解:(1)因为△ABC是由△A1B1C1向右平移3个单位,再向下平移1个单位所得
所以,△A1B1C1是由△ABC向左平移3个单位,再向上平移1个单位所得A1(﹣1,2),B1(2,4),C1 (0,5);
(2)如图,△ABC的面积=3×3﹣×1×3﹣×1×2﹣×2×3=3.5.
20.解:(1)△ABO的面积=×1×3+×(1+3)×2﹣×3×1=4;
(2)点A1和点B重合时,需将△ABC向右移2个单位,向下移2个单位,
∴点O的对应点O1的坐标是(2,﹣2),
答案为:(2,﹣2);
(3)平移△ABO至△A2B2O2,需要至少向下平移超过3单位,并且至少向左平移超过3个单位,才能使△A2B2O2位于第三象限.
答案为:3,3.
21.解:(1)∵点P在y轴上,
∴2m﹣6=0,解得m=3,
∴P点的坐标为(0,5);
答案为(0,5);
(2)根据题意得2m﹣6+6=m+2,解得m=2,
∴P点的坐标为(﹣2,4),
∴点P在第二象限;
(3)∵点Q在过A(2,3)点且与x轴平行的直线上,
∴点Q的纵坐标为3,
而AQ=3,
∴Q点的横坐标为﹣1或5,
∴Q点的坐标为(﹣1,3)或(5,3).
22.解:(1)如图所示:点A的坐标为(﹣4,2);
答案为:(﹣4,2);
(2)如图所示:△A1B1C1,即为所求;
(3)△A1B1C1的面积为:3×4﹣×1×3﹣×2×3﹣×1×4=5.5.
答案为:5.5.
一.选择题
1.在平面直角坐标系中,将点P(﹣3,2)向左平移2个单位长度后得到的点的坐标为( )
A.(﹣5,2) B.(﹣3,﹣1) C.(﹣3,4) D.(﹣1,2)
2.下列说法正确的是( )
A.若点A(3,﹣1),则点A到x轴的距离为3
B.平行于y轴的直线上所有点的纵坐标都相同
C.(﹣2,2)与(2,﹣2)表示两个不同的点
D.若点Q(a,b)在x轴上,则a=0
3.如图所示的象棋盘上,若“帅”位于点(1,﹣2)上,“相”位于点(3,﹣2)上,则“炮”位于点( )
A.(﹣2,1) B.(﹣1,2) C.(﹣1,1) D.(﹣2,2)
4.在平面直角坐标系中,将点P(﹣1,0)向右平移2个单位,再向上平移2个单位,得到点P′,则点P′在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知点A(0,﹣6),点B(0,3),则A,B两点间的距离是( )
A.﹣9 B.9 C.﹣3 D.3
6.在平面直角坐标系中,点A的坐标为(﹣4,3),AB∥y轴,AB=5,则点B的坐标为( )
A.(1,3) B.(﹣4,8)
C.(﹣4,8)或(﹣4,﹣2) D.(1,3)或(﹣9,3)
7.已知小明从点O出发,先向西走10米,再向南走20米,到达点M,如果点M的位置用(﹣10,﹣20)表示,那么(10,﹣10)表示的位置是( )
A.点A B.点B C.点C D.点D
8.在平面直角坐标系中,把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是( )
A.向上平移3个单位 B.向下平移3个单位
C.向左平移3个单位 D.向右平移3个单位
9.在平面直角坐标系内,将M(5,2)先向下平移2个单位,再向左平移3个单位,则移动后的点的坐标是( )
A.(2,0) B.(3,5) C.(8,4) D.(2,3)
10.在平面直角坐标系中,将点A(0,1)做如下的连续平移,第1次向右平移得到点A1(1,1),第2次向下平移得到点A2(1,﹣1),第3次向右平移得到点A3(4,﹣1),第4次向下平移得到点A4(4,﹣5)….按此规律平移下去,则A15的点坐标是( )
A.(64,﹣55) B.(65,﹣53) C.(66,﹣56) D.(67,﹣58)
二.填空题
11.一只蚂蚁由点(2,3)先向上爬2个单位长度,再向右爬4个单位长度,再向下爬1个单位长度后,它所在位置的坐标是 .
12.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为 .
13.如图是一台雷达探测相关目标得到的部分结果,若图中目标A的位置为(2,90°),目标B的位置为(4,210°),则目标C的位置为 .
14.若点P(2﹣m,﹣1),将P点向右平移2个单位长度后落在y轴上,则m= .
15.如图,点A、B分别在x轴和y轴上,OA=1,OB=2,若将线段AB平移至A'B',则a+b的值为 .
16.在平面直角坐标系中,若点M(2,4)与点N(x,4)之间的距离是3,则x的值是 .
三.解答题
17.如图所示的是某市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度),若海洋极地公园的坐标为(4,0),大唐芙蓉园的坐标为(2,﹣1),请建立平面直角坐标系,并用坐标表示大明宫国家遗址公园的位置.
18.如图,在边长为1个单位长度的小正方形组成的网格中,小明家可用坐标(﹣1,2)表示,汽车站可用坐标(3,﹣1)表示.
(1)建立平面直角坐标系,画出x轴和y轴;
(2)某星期日早晨,小明同学从家出发,沿(0,1)→(﹣2,﹣1)→(﹣1,﹣2)→(0,﹣1)→(1,0)→(2,﹣1)→(2,2)的路线转了一圈,又回到家里,写出他路上经过的地方;
(3)连接他在上一问中经过的地点,你得到了什么图形?
19.如图,△ABC是由△A1B1C1向右平移3个单位,再向下平移1个单位所得.已知A(2,1),B(5,3),C(3,4).
(1)直接写出△A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
20.已知坐标平面内的三个点A(1,3)、B(3,1)、O(0,0).
(1)求△ABO的面积;
(2)平移△ABO至△A1B1O1,当点A1和点B重合时,点O1的坐标是 ;
(3)平移△ABO至△A2B2O2,需要至少向下平移超过 单位,并且至少向左平移 个单位,才能使△A2B2O2位于第三象限.
21.已知,点P(2m﹣6,m+2).
(1)若点P在y轴上,P点的坐标为 ;
(2)若点P的纵坐标比横坐标大6,求点P在第几象限?
(3)若点P和点Q都在过A(2,3)点且与x轴平行的直线上,AQ=3,求Q点的坐标.
22.按要求画图及填空:
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
(1)点A的坐标为 ;
(2)将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1,画出△A1B1C1.
(3)△A1B1C1的面积为 .
参考答案
一.选择题
1.解:将点P(﹣3,2)向左平移2个单位长度得到的点坐标为(﹣3﹣2,2),即(﹣5,2),
选:A.
2.解:A、若点A(3,﹣1),则点A到x轴的距离应该是1,本选项错误,不符合题意.
B、平行于y轴的直线上所有点的纵坐标都相同,错误,应该是横坐标相同,本选项不符合题意.
C、(﹣2,2)与(2,﹣2)表示两个不同的点,正确,本选项符合题意.
D、若点Q(a,b)在x轴上,应该是b=0,本选项错误,不符合题意.
选:C.
3.解:如图所示:则“炮”位于点(﹣2,1).
选:A.
4.解:由题意,P′(﹣1+2,0+2),即P′(1,2),在第一象限,
选:A.
5.解:∵A(0,﹣6),点B(0,3),
∴A,B两点间的距离=3﹣(﹣6)=9.
选:B.
6.解:∵AB∥y轴,
∴A、B两点的横坐标相同,
又AB=5,
∴B点纵坐标为:3+5=8或3﹣5=﹣2,
∴B点的坐标为:(﹣4,﹣2)或(﹣4,8);
选:C.
7.解:∵点M的位置用(﹣10,﹣20)表示,
∴(10,﹣10)表示D点.
选:D.
8.解:把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是向左平移3个单位,
选:C.
9.解:平移后的坐标为(5﹣3,2﹣2),即坐标为(2,0),
选:A.
10.解:由题意,可知点A第15次平移至点A15的横坐标是0+1+3+5+7+9+11+13+15=64,纵坐标是1﹣2﹣4﹣6﹣8﹣10﹣12﹣14=﹣55,
即点A15的坐标是(64,﹣55).
选:A.
二.填空题
11.解:点(2,3)先向上爬2个单位长度,所得点的坐标为(2,5),
再向右爬4个单位长度,所得点的坐标为(6,5),
再向下爬1个单位长度后,所得点的坐标为(6,4),
答案为:(6,4).
12.解:∵棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3)
∴坐标系的原点为O,如图所示,
∴棋子“炮”的坐标为(3,2).答案填:(3,2).
13.解:由题意,点C的位置为(3,150°).
答案为(3,150°).
14.解:点P(2﹣m,﹣1),将P点向右平移2个单位长度后点的坐标为(4﹣m,﹣1),
∵向右平移2个单位长度后落在y轴上,
∴4﹣m=0,
解得:m=4,
答案为:4.
15.解:由作图可知,线段AB向右平移3个单位,再向下平移1个单位得到线段A′B′,
∵A(﹣1,0),B(0,2),
∴A′(2,﹣1),B′(3,1),
∴a=﹣1,b=3,
∴a+b=2,
答案为:2.
16.解:∵点M(2,4)与点N(x,4)之间的距离是3,
∴|2﹣x|=3,
解得,x=﹣1或x=5,
答案为:﹣1或5.
三.解答题
17.解:如图所示:
大明宫国家遗址公园(1,5).
18.解:(1)如图,建立平面直角坐标系;
(2)小明家﹣学校﹣奶奶家﹣宠物店﹣医院﹣公园﹣邮局﹣游乐场﹣消防站﹣小明家;
(3)连接他在上一问中经过的地点,得到“箭头”状的图形.
19.解:(1)因为△ABC是由△A1B1C1向右平移3个单位,再向下平移1个单位所得
所以,△A1B1C1是由△ABC向左平移3个单位,再向上平移1个单位所得A1(﹣1,2),B1(2,4),C1 (0,5);
(2)如图,△ABC的面积=3×3﹣×1×3﹣×1×2﹣×2×3=3.5.
20.解:(1)△ABO的面积=×1×3+×(1+3)×2﹣×3×1=4;
(2)点A1和点B重合时,需将△ABC向右移2个单位,向下移2个单位,
∴点O的对应点O1的坐标是(2,﹣2),
答案为:(2,﹣2);
(3)平移△ABO至△A2B2O2,需要至少向下平移超过3单位,并且至少向左平移超过3个单位,才能使△A2B2O2位于第三象限.
答案为:3,3.
21.解:(1)∵点P在y轴上,
∴2m﹣6=0,解得m=3,
∴P点的坐标为(0,5);
答案为(0,5);
(2)根据题意得2m﹣6+6=m+2,解得m=2,
∴P点的坐标为(﹣2,4),
∴点P在第二象限;
(3)∵点Q在过A(2,3)点且与x轴平行的直线上,
∴点Q的纵坐标为3,
而AQ=3,
∴Q点的横坐标为﹣1或5,
∴Q点的坐标为(﹣1,3)或(5,3).
22.解:(1)如图所示:点A的坐标为(﹣4,2);
答案为:(﹣4,2);
(2)如图所示:△A1B1C1,即为所求;
(3)△A1B1C1的面积为:3×4﹣×1×3﹣×2×3﹣×1×4=5.5.
答案为:5.5.
