2021年人教版八年级下册:18.2.1矩形同步练习试卷(Word版含答案)
文档属性
| 名称 | 2021年人教版八年级下册:18.2.1矩形同步练习试卷(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 07:59:03 | ||
图片预览


文档简介
2021年人教版八年级下册:18.2.1《矩形》同步练习
一.选择题
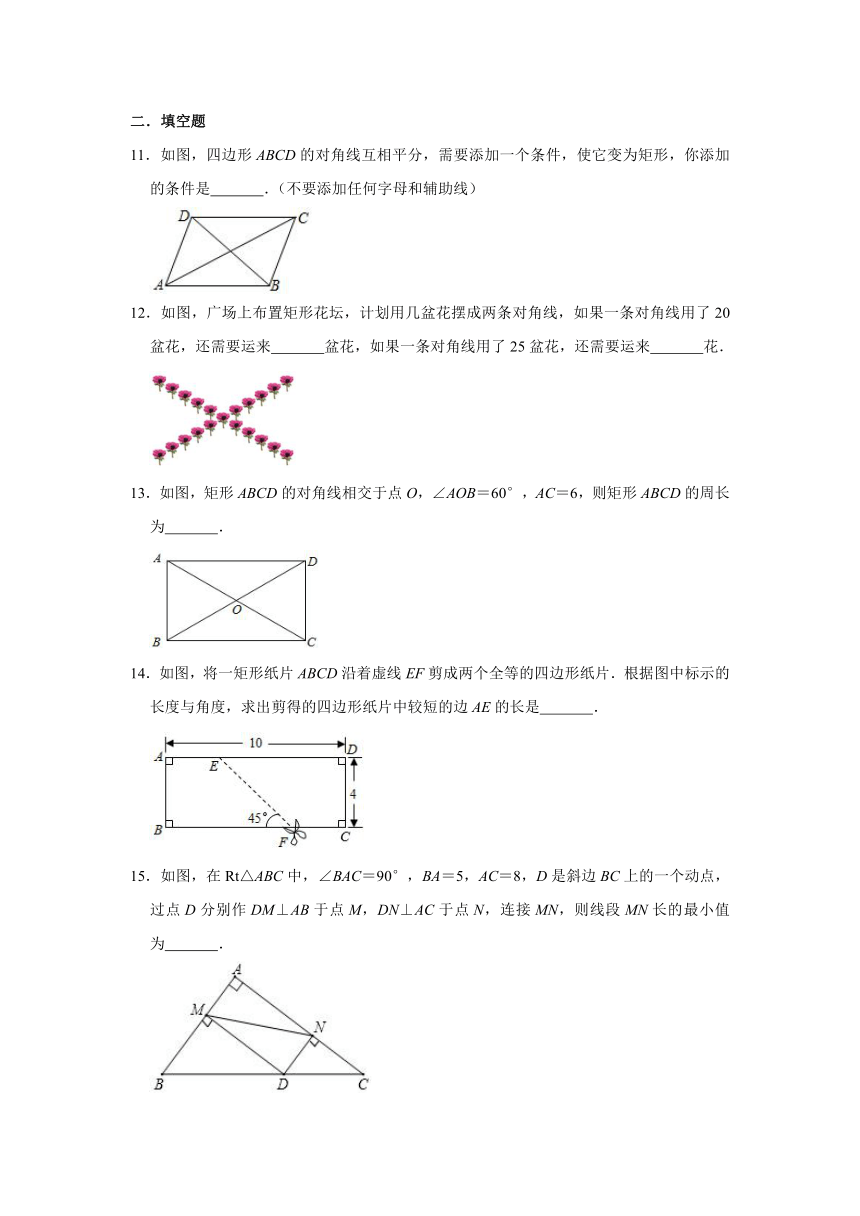
1.下列说法正确的是( )
A.矩形的对角线互相垂直且平分
B.矩形的邻边一定相等
C.对角线相等的四边形是矩形
D.有三个角为直角的四边形为矩形
2.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OCD的度数为( )
A.35° B.40° C.45° D.50°
3.平行四边形ABCD的对角线AC和BD交于点O,添加一个条件不能使平行四边形ABCD变为矩形的是( )
A.OD=OC B.∠DAB=90° C.∠ODA=∠OAD D.AC⊥BD
4.如图,矩形ABCD的对角线AC、BD交于点O,M、N分别为BC、OC的中点,AB=6,∠ACB=30°则MN的长为( )
A.3 B.4 C.5 D.6
5.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.CE⊥DE C.∠ADB=90° D.BE⊥DC
6.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
7.矩形ABCD中,点M在对角线AC上,过M作AB的平行线交AD于E,交BC于F,连接DM和BM,已知,DE=2,ME=4,则图中阴影部分的面积是( )
A.12 B.10 C.8 D.6
8.如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
9.如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是( )
A. B.3 C. D.5
10.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
二.填空题
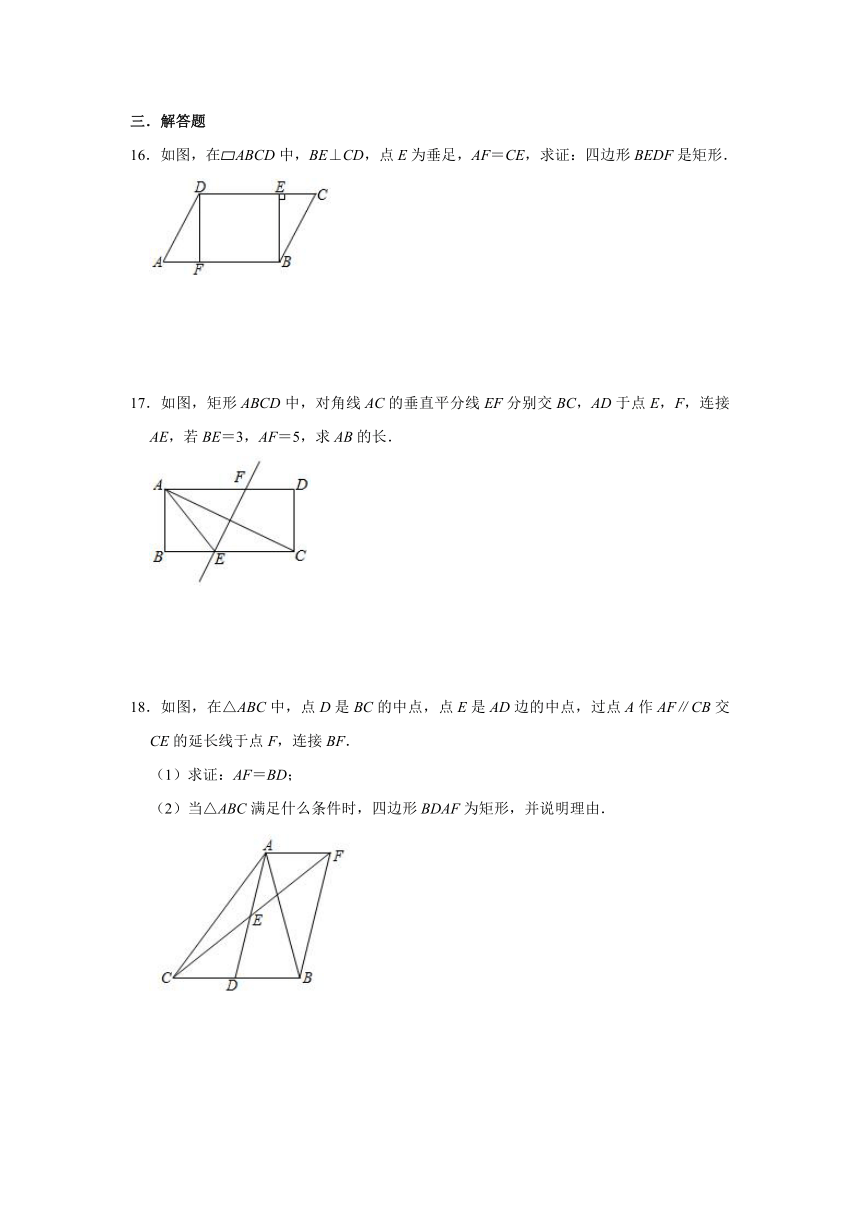
11.如图,四边形ABCD的对角线互相平分,需要添加一个条件,使它变为矩形,你添加的条件是 .(不要添加任何字母和辅助线)
12.如图,广场上布置矩形花坛,计划用几盆花摆成两条对角线,如果一条对角线用了20盆花,还需要运来 盆花,如果一条对角线用了25盆花,还需要运来 花.
13.如图,矩形ABCD的对角线相交于点O,∠AOB=60°,AC=6,则矩形ABCD的周长为 .
14.如图,将一矩形纸片ABCD沿着虚线EF剪成两个全等的四边形纸片.根据图中标示的长度与角度,求出剪得的四边形纸片中较短的边AE的长是 .
15.如图,在Rt△ABC中,∠BAC=90°,BA=5,AC=8,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN长的最小值为 .
三.解答题
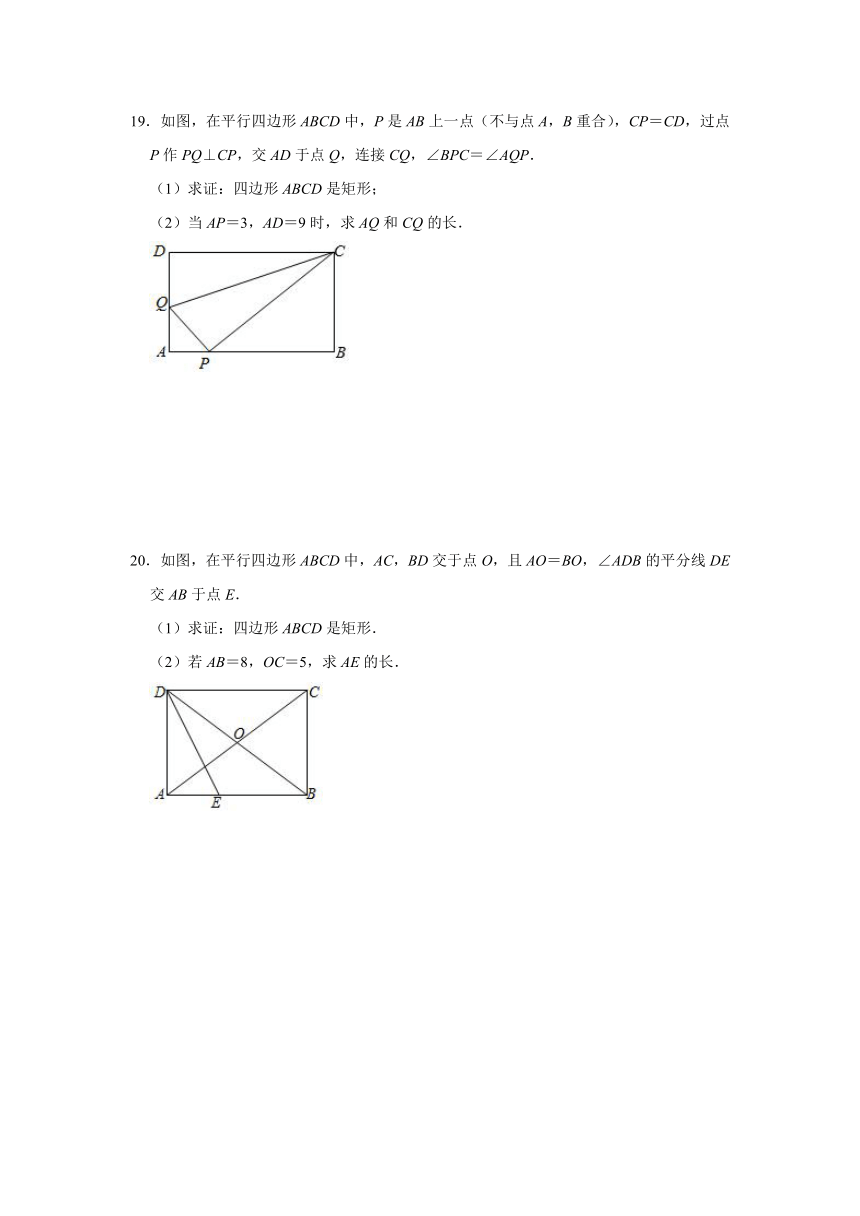
16.如图,在?ABCD中,BE⊥CD,点E为垂足,AF=CE,求证:四边形BEDF是矩形.
17.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,连接AE,若BE=3,AF=5,求AB的长.
18.如图,在△ABC中,点D是BC的中点,点E是AD边的中点,过点A作AF∥CB交CE的延长线于点F,连接BF.
(1)求证:AF=BD;
(2)当△ABC满足什么条件时,四边形BDAF为矩形,并说明理由.
19.如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ,∠BPC=∠AQP.
(1)求证:四边形ABCD是矩形;
(2)当AP=3,AD=9时,求AQ和CQ的长.
20.如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
参考答案
一.选择题
1.解:A、∵矩形的对角线互相平分且相等,
∴选项A不符合题意;
B、∵矩形的邻边一定垂直,不一定相等,
∴选项B不符合题意;
C、∵对角线相等的平行四边形是矩形,
∴选项C不符合题意;
D、∵有三个角为直角的四边形为矩形,
∴选项D符合题意;
选:D.
2.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠DAB=90°,AB∥CD,
∴∠OAB=∠DAB﹣∠OAD=90°﹣55°=35°,∠OCD=∠OAB=35°,
选:A.
3.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
A、OD=OC时,AC=BD,
∴平行四边形ABCD是矩形,选项A不符合题意;
B、四边形ABCD是平行四边形,∠DAB=90°,
∴平行四边形ABCD是矩形,选项B不符合题意;
C、∵∠ODA=∠OAD,
∴OA=OD,
∴AC=BD,
∴平行四边形ABCD是矩形,选项C不符合题意;
D、四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,选项D符合题意;
选:D.
4.解:∵四边形ABCD是矩形,
∴AO=CO=BO=DO,∠ABC=90°,
∵∠ACB=30°,
∴∠BAC=60°,
∴△ABO是等边三角形,
∴BO=AB=6,
∵M、N分别为BC、OC的中点,
∴MN=BO=3,
选:A.
5.解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又∵AD=DE,
∴DE∥BC,且DE=BC,
∴四边形BCED为平行四边形,
A、∵AB=BE,DE=AD,
∴BD⊥AE,
∴?DBCE为矩形,本选项不符合题意;
B、∵CE⊥DE,
∴∠CED=90°,
∴?DBCE为矩形,本选项不符合题意;
C、∵∠ADB=90°,
∴∠EDB=90°,
∴?DBCE为矩形,本选项不符合题意;
D、∵对角线互相垂直的平行四边形为菱形,不一定为矩形,本选项符合题意;
选:D.
6.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
选:C.
7.解:过M作MP⊥AB于P,交DC于Q,如图所示:
则四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC﹣S△AMP﹣S△MCF=S△ADC﹣S△AEM﹣S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×4=4,
∴S阴=4+4=8,
选:C.
8.解:∵四边形ABCD是矩形,
∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,
∴DE=DC=2,
∴EC=2,
∵∠DCE=45°,
∴∠DEC=45°,
∵EB平分∠AEC,
∴∠BEC=∠AEB=∠AEC=,
∴∠EBC=180°﹣67.5°﹣45°=67.5°,
∴∠BEC=∠EBC,
∴BC=CE=2,
∴AD=BC=2,
∴AE=AD﹣DE=2﹣2,
选:B.
9.解:如图,连接AC,OB,
∵四边形AOCB是矩形,
∴AC=OB,
∵点B的坐标是(2,5),点O(0,0),
∴OB==,
∴A,C两点间的距离为,
选:C.
10.解:∵四边形ABCD是矩形,
∴OA=OB=OD,
∵∠AOD=120°,
∴∠AOB=180°﹣120°=60°,
∴△AOB为等边三角形,
∵AE⊥BD,
∴BE=OE=OB,
∴ED=3BE,
∴=,
选:A.
二.填空题
11.解:∵四边形ABCD的对角线互相平分,
∴四边形ABCD为平行四边形,
添加条件:AC=BD或∠ABC=90°或∠BCD=90°或∠CDA=90°或∠DAB=90°时,四边形ABCD是矩形;
答案为:AC=BD或∠ABC=90°或∠BCD=90°或∠CDA=90°或∠DAB=90°.
12.解:如果一条对角线用了20盆红花,还需要从花房运来20盆红花;理由如下:
∵矩形的对角线互相平分且相等,
∴一条对角线用了20盆花,
∴还需要从花房运来花20盆;
如果一条对角线用了25盆红花,还需要从花房运来24盆红花;理由如下:
一条对角线用了25盆红花,中间一盆为对角线交点,25﹣1=24,
∴还需要从花房运来红花24盆,
答案为:20,24.
13.解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC=6,OA=AC=3,BO=BD=3,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB=3,
∴BC===3,
∴矩形ABCD的周长=2(AB+BC)=2×(3+3)=.
答案为:.
14.解:过F作FQ⊥AD于Q,则∠FQE=90°,
∵四边形ABCD是长方形,
∴∠A=∠B=90°,AB=DC=4,AD∥BC,
∴四边形ABFQ是矩形,
∴AB=FQ=DC=4,
∵AD∥BC,
∴∠QEF=∠BFE=45°,
∴EQ=FQ=4,
∴AE=CF=×(10﹣4)=3,
答案为:3.
15.解:∵∠BAC=90°,且BA=5,AC=8,
∴BC===,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD===,
∴MN的最小值为,
答案为:.
三.解答题
16.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形BEDF是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形BEDF是矩形.
17.解:∵EF是AC的垂直平分线,
∴AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≡△COE(ASA),
∴AF=CE=5,
∵EF是AC的垂直平分线,
∴AE=CE=5,
Rt△ABE中,∵BE=3,
∴AB==4.
18.(1)证明:∵点D是BC的中点,点E是AD边的中点,
∴DE是△CBF的中位线,
∴DE∥BF,
∴AD∥BF,
∵AF∥CB,
∴AF∥DB,
∴四边形BDAF为平行四边形,
∴AF=BD;
(2)解:△ABC满足:AB=AC时,四边形BDAF为矩形,
理由如下:
∵AB=AC,BD=BD,
∴∠ADB=90°,
由(1)知四边形BDAF为平行四边形,
∴?BDAF为矩形.
19.(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,
∴∠A=∠CPQ=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴DQ=PQ,
设AQ=x,则DQ=PQ=12﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,
∴x2+32=(9﹣x)2,
解得:x=4,
∴AQ的长是4.
设CD=AB=CP=y,则PB=y﹣3,在Rt△PCB中,根据勾股定理列方程,求出y=15.
在Rt△CDQ中,CQ==5.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AC=2AO,BD=2BO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD为矩形;
(2)解:过点E作EG⊥BD于点G,如图所示:
∵四边形ABCD是矩形,OC=5,
∴∠BAD=90°,BD=AC=2OC=10.
在Rt△ABD中,AB=8,BD=10,
∴AD===6,
∵∠DAB=90°,
∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,
∴EG=EA,∠EGB=90°.
在Rt△ADE和Rt△GDE中,
,
∴Rt△ADE≌Rt△GDE(HL),
∴AD=GD=6,
∴BG=BD﹣GD=10﹣6=4,
在Rt△BEG中,由勾股定理得:BE2=EG2+BG2,
即(8﹣AE)2=AE2+42,
解得:AE=3.
一.选择题
1.下列说法正确的是( )
A.矩形的对角线互相垂直且平分
B.矩形的邻边一定相等
C.对角线相等的四边形是矩形
D.有三个角为直角的四边形为矩形
2.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OCD的度数为( )
A.35° B.40° C.45° D.50°
3.平行四边形ABCD的对角线AC和BD交于点O,添加一个条件不能使平行四边形ABCD变为矩形的是( )
A.OD=OC B.∠DAB=90° C.∠ODA=∠OAD D.AC⊥BD
4.如图,矩形ABCD的对角线AC、BD交于点O,M、N分别为BC、OC的中点,AB=6,∠ACB=30°则MN的长为( )
A.3 B.4 C.5 D.6
5.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.CE⊥DE C.∠ADB=90° D.BE⊥DC
6.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
7.矩形ABCD中,点M在对角线AC上,过M作AB的平行线交AD于E,交BC于F,连接DM和BM,已知,DE=2,ME=4,则图中阴影部分的面积是( )
A.12 B.10 C.8 D.6
8.如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
9.如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是( )
A. B.3 C. D.5
10.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
二.填空题
11.如图,四边形ABCD的对角线互相平分,需要添加一个条件,使它变为矩形,你添加的条件是 .(不要添加任何字母和辅助线)
12.如图,广场上布置矩形花坛,计划用几盆花摆成两条对角线,如果一条对角线用了20盆花,还需要运来 盆花,如果一条对角线用了25盆花,还需要运来 花.
13.如图,矩形ABCD的对角线相交于点O,∠AOB=60°,AC=6,则矩形ABCD的周长为 .
14.如图,将一矩形纸片ABCD沿着虚线EF剪成两个全等的四边形纸片.根据图中标示的长度与角度,求出剪得的四边形纸片中较短的边AE的长是 .
15.如图,在Rt△ABC中,∠BAC=90°,BA=5,AC=8,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN长的最小值为 .
三.解答题
16.如图,在?ABCD中,BE⊥CD,点E为垂足,AF=CE,求证:四边形BEDF是矩形.
17.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,连接AE,若BE=3,AF=5,求AB的长.
18.如图,在△ABC中,点D是BC的中点,点E是AD边的中点,过点A作AF∥CB交CE的延长线于点F,连接BF.
(1)求证:AF=BD;
(2)当△ABC满足什么条件时,四边形BDAF为矩形,并说明理由.
19.如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ,∠BPC=∠AQP.
(1)求证:四边形ABCD是矩形;
(2)当AP=3,AD=9时,求AQ和CQ的长.
20.如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
参考答案
一.选择题
1.解:A、∵矩形的对角线互相平分且相等,
∴选项A不符合题意;
B、∵矩形的邻边一定垂直,不一定相等,
∴选项B不符合题意;
C、∵对角线相等的平行四边形是矩形,
∴选项C不符合题意;
D、∵有三个角为直角的四边形为矩形,
∴选项D符合题意;
选:D.
2.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠DAB=90°,AB∥CD,
∴∠OAB=∠DAB﹣∠OAD=90°﹣55°=35°,∠OCD=∠OAB=35°,
选:A.
3.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
A、OD=OC时,AC=BD,
∴平行四边形ABCD是矩形,选项A不符合题意;
B、四边形ABCD是平行四边形,∠DAB=90°,
∴平行四边形ABCD是矩形,选项B不符合题意;
C、∵∠ODA=∠OAD,
∴OA=OD,
∴AC=BD,
∴平行四边形ABCD是矩形,选项C不符合题意;
D、四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,选项D符合题意;
选:D.
4.解:∵四边形ABCD是矩形,
∴AO=CO=BO=DO,∠ABC=90°,
∵∠ACB=30°,
∴∠BAC=60°,
∴△ABO是等边三角形,
∴BO=AB=6,
∵M、N分别为BC、OC的中点,
∴MN=BO=3,
选:A.
5.解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又∵AD=DE,
∴DE∥BC,且DE=BC,
∴四边形BCED为平行四边形,
A、∵AB=BE,DE=AD,
∴BD⊥AE,
∴?DBCE为矩形,本选项不符合题意;
B、∵CE⊥DE,
∴∠CED=90°,
∴?DBCE为矩形,本选项不符合题意;
C、∵∠ADB=90°,
∴∠EDB=90°,
∴?DBCE为矩形,本选项不符合题意;
D、∵对角线互相垂直的平行四边形为菱形,不一定为矩形,本选项符合题意;
选:D.
6.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
选:C.
7.解:过M作MP⊥AB于P,交DC于Q,如图所示:
则四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC﹣S△AMP﹣S△MCF=S△ADC﹣S△AEM﹣S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×4=4,
∴S阴=4+4=8,
选:C.
8.解:∵四边形ABCD是矩形,
∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,
∴DE=DC=2,
∴EC=2,
∵∠DCE=45°,
∴∠DEC=45°,
∵EB平分∠AEC,
∴∠BEC=∠AEB=∠AEC=,
∴∠EBC=180°﹣67.5°﹣45°=67.5°,
∴∠BEC=∠EBC,
∴BC=CE=2,
∴AD=BC=2,
∴AE=AD﹣DE=2﹣2,
选:B.
9.解:如图,连接AC,OB,
∵四边形AOCB是矩形,
∴AC=OB,
∵点B的坐标是(2,5),点O(0,0),
∴OB==,
∴A,C两点间的距离为,
选:C.
10.解:∵四边形ABCD是矩形,
∴OA=OB=OD,
∵∠AOD=120°,
∴∠AOB=180°﹣120°=60°,
∴△AOB为等边三角形,
∵AE⊥BD,
∴BE=OE=OB,
∴ED=3BE,
∴=,
选:A.
二.填空题
11.解:∵四边形ABCD的对角线互相平分,
∴四边形ABCD为平行四边形,
添加条件:AC=BD或∠ABC=90°或∠BCD=90°或∠CDA=90°或∠DAB=90°时,四边形ABCD是矩形;
答案为:AC=BD或∠ABC=90°或∠BCD=90°或∠CDA=90°或∠DAB=90°.
12.解:如果一条对角线用了20盆红花,还需要从花房运来20盆红花;理由如下:
∵矩形的对角线互相平分且相等,
∴一条对角线用了20盆花,
∴还需要从花房运来花20盆;
如果一条对角线用了25盆红花,还需要从花房运来24盆红花;理由如下:
一条对角线用了25盆红花,中间一盆为对角线交点,25﹣1=24,
∴还需要从花房运来红花24盆,
答案为:20,24.
13.解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC=6,OA=AC=3,BO=BD=3,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB=3,
∴BC===3,
∴矩形ABCD的周长=2(AB+BC)=2×(3+3)=.
答案为:.
14.解:过F作FQ⊥AD于Q,则∠FQE=90°,
∵四边形ABCD是长方形,
∴∠A=∠B=90°,AB=DC=4,AD∥BC,
∴四边形ABFQ是矩形,
∴AB=FQ=DC=4,
∵AD∥BC,
∴∠QEF=∠BFE=45°,
∴EQ=FQ=4,
∴AE=CF=×(10﹣4)=3,
答案为:3.
15.解:∵∠BAC=90°,且BA=5,AC=8,
∴BC===,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD===,
∴MN的最小值为,
答案为:.
三.解答题
16.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形BEDF是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形BEDF是矩形.
17.解:∵EF是AC的垂直平分线,
∴AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≡△COE(ASA),
∴AF=CE=5,
∵EF是AC的垂直平分线,
∴AE=CE=5,
Rt△ABE中,∵BE=3,
∴AB==4.
18.(1)证明:∵点D是BC的中点,点E是AD边的中点,
∴DE是△CBF的中位线,
∴DE∥BF,
∴AD∥BF,
∵AF∥CB,
∴AF∥DB,
∴四边形BDAF为平行四边形,
∴AF=BD;
(2)解:△ABC满足:AB=AC时,四边形BDAF为矩形,
理由如下:
∵AB=AC,BD=BD,
∴∠ADB=90°,
由(1)知四边形BDAF为平行四边形,
∴?BDAF为矩形.
19.(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,
∴∠A=∠CPQ=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴DQ=PQ,
设AQ=x,则DQ=PQ=12﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,
∴x2+32=(9﹣x)2,
解得:x=4,
∴AQ的长是4.
设CD=AB=CP=y,则PB=y﹣3,在Rt△PCB中,根据勾股定理列方程,求出y=15.
在Rt△CDQ中,CQ==5.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AC=2AO,BD=2BO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD为矩形;
(2)解:过点E作EG⊥BD于点G,如图所示:
∵四边形ABCD是矩形,OC=5,
∴∠BAD=90°,BD=AC=2OC=10.
在Rt△ABD中,AB=8,BD=10,
∴AD===6,
∵∠DAB=90°,
∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,
∴EG=EA,∠EGB=90°.
在Rt△ADE和Rt△GDE中,
,
∴Rt△ADE≌Rt△GDE(HL),
∴AD=GD=6,
∴BG=BD﹣GD=10﹣6=4,
在Rt△BEG中,由勾股定理得:BE2=EG2+BG2,
即(8﹣AE)2=AE2+42,
解得:AE=3.
