上海市奉贤区2020-2021学年八年级上学期期末数学试题(Word版 含解析)
文档属性
| 名称 | 上海市奉贤区2020-2021学年八年级上学期期末数学试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 790.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-08 10:52:11 | ||
图片预览




文档简介
上海市奉贤区2020-2021学年八年级上学期期末数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.下列关于x的方程一定有实数根的是( )
A. B. C. D.
4.学校升旗仪式上,徐徐上升的国旗的高度与时间的关系可以用下面的一个函数图像近似地刻画,这个函数图像是( )
A. B.
C. D.
5.下列定理有逆定理的是( )
A.对顶角相等 B.直角三角形两锐角互余
C.全等三角形的对应角相等 D.全等三角形的面积相等
6.如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,以下判断中正确的个数有( )
①∠DCB=∠A;②∠DCB=∠ACE;③∠ACD=∠BCE;④∠BCE=∠BEC.
A.1个 B.2个 C.3个 D.4个
二、填空题
7.计算: =_____.
8.函数的定义域是_____.
9.方程的根是____________.
10.关于x的一元二次方程有两个不相等的实数根,则k的取值范围是________.
11.在实数范围内分解因式:______.
12.已知直角坐标平面内的点,和,那么的形状是______.
13.已知反比例函数的图像上有两点,,那么______.(填“>”或“<”)
14.已知函数,那么______.
15.随着人们生活水平的不断提高,汽车逐步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有_______处.
16.如图.在中,,,以直角顶点为圆心,长为半径画弧交于点,过点作于点,若,则的周长用含的代数式表示为_______________.
17.我们定义:一个三角形最小内角的角平分线将这个三角形分割得到的两个三角形它们的面积之比称为“最小角割比Ω”(),那么三边长分别为7,24,25的三角形的最小角割比Ω是______.
18.在中,,,将绕点C旋转得到,点A,B分别与,对应,当时,记直线与直线交点为E,那么 的度数是______.
三、解答题
19.计算:
20.解方程:
21.某口罩厂2020年1月口罩生产数量40万个,2月份口罩产量增长了25%,为应对“新冠”疫情,计划通过两个月进行产能爬坡,预计到4月份时月产量达到60.5万个,求该口罩厂这两个月口罩生产数量的月平均增长率.
22.如图,中,,.
(1)利用直尺,圆规在边上找一点E,使得;(不需要写作法,但要保留作图痕迹)
(2)若厘米,求的长.
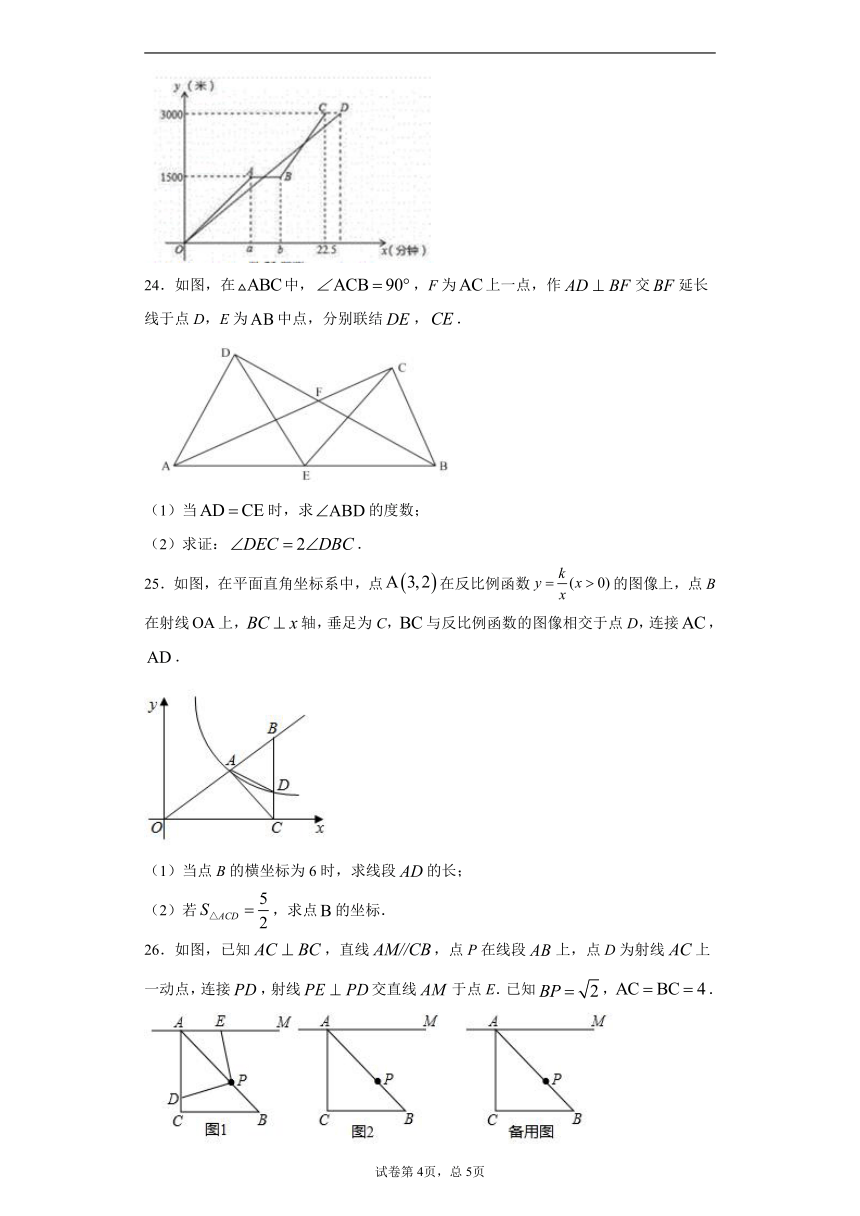
23.为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度到达图书馆,而妈妈始终以120米/分钟的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图像,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2)a= ,b= ,m= ;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是 ;定义域是 .
24.如图,在中,,F为上一点,作交延长线于点D,E为中点,分别联结,.
(1)当时,求的度数;
(2)求证:.
25.如图,在平面直角坐标系中,点在反比例函数的图像上,点B在射线上,轴,垂足为C,与反比例函数的图像相交于点D,连接,.
(1)当点B的横坐标为6时,求线段的长;
(2)若,求点的坐标.
26.如图,已知,直线,点P在线段上,点D为射线上一动点,连接,射线交直线于点E.已知,.
(1)如图1,当点D在线段上时,求证:;
(2)当时,请在图2中画出相应的图形,并求线段的长;
(3)如果的平分线交射线于点G,设,,求y关于x的函数关系式,并写出自变量x的取值范围.
参考答案
1.D
【分析】
根据二次根式的性质把各个二次根式化简,根据同类二次根式的概念判断即可.
【详解】
解:A、,与不是同类二次根式;
B、,与不是同类二次根式;
C、,与不是同类二次根式;
D、,与是同类二次根式;
故选:D.
【点睛】
本题考查的是同类二次根式的概念、二次根式的化简,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式.
2.D
【分析】
根据二次根式的加减法、乘除法法则和算术平方根的意义分别判断.
【详解】
解:A、无法合并计算,故错误;
B、,故错误;
C、,故错误;
D、,故正确.
故选D.
【点睛】
本题考查了二次根式的运算,解题的关键是掌握运算法则.
3.A
【分析】
分别根据方程的解得定义,从a的取值出发进行判断.
【详解】
解:A、有实数解,故符合;
B、,当a=0时,等式不成立,即方程无实数解,故不符合;
C、,当a=0时,等式不成立,即方程无实数解,故不符合;
D、,当a<0时,等式不成立,即方程无实数解,故不符合;
故选A.
【点睛】
本题考查了方程的解,解题的关键是理解方程的解的定义,对a值进行取值验证.
4.B
【分析】
根据国旗上升的高度随着时间的增长而逐渐变大可得出答案.
【详解】
国旗上升的高度随着时间的增长而逐渐变大,可知图象如B选项,
故选:B.
【点睛】
本题主要考查函数的图象,掌握生活常识是关键.
5.B
【分析】
先分别写出第个选项的逆命题,再判断其是否正确.
【详解】
解:A的逆命题是:相等的角是对顶角,假命题;
B的逆命题是:两锐角互余的三角形是直角三角形,真命题;
C的逆命题是:面积相等的三角形是全等三角形,假命题;
D的逆命题是:对应角相等的三角形是全等三角形,假命题;
故选:B.
【点睛】
本题主要考查了学生对逆命题以及真假命题的定义的理解,要求学生对常用的基础知识牢固掌握,比较简单.
6.C
【分析】
根据垂直的定义得到∠CDB=90°,根据余角的性质得到∠DCB=∠A,故①正确;根据直角三角形的性质得到AE=CE=BE,根据等腰三角形的性质得到∠A=∠ACE,于是得到∠DCB=∠ACE,故②正确;同理得到∠ACD=∠BCE,故③正确;由于BC不一定等于BE,于是得到∠BCE不一定等于∠BEC,故④错误.
【详解】
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB+B=90°,
∵∠A+∠B=90,
∴∠DCB=∠A,
∴①正确;
∵CE是RtABC斜边AB上的中线,
∴EA=EC=EB,
∴∠ACE=∠A,
∴∠DCB=∠A,
∴∠DCB=∠ACE,
∴②正确;
∵EC=EB,
∴∠B=∠BCE,
∵∠A+∠B=90,∠A+∠ACD=90,
∴∠B= ∠ACD,
∴∠ACD= ∠BCE,
∴③正确;
∵BC与BE不一定相等,
∴∠BCE 与∠BEC 不一定相等,
∴④不正确;
∴正确的个数为3个,
故答案为C.
【点睛】
本题考查了直角三角形的性质,熟练掌握直角三角形的性质是解题的关键.
7.
【分析】
根据立方根的意义求解即可.
【详解】
.
8.x≥.
【分析】
根据二次根式有意义的条件:被开方数大于或等于0,即可求出x的范围.
【详解】
解:根据题意得:2x﹣1≥0,解得:x≥.
故答案为x≥.
【点睛】
本题考查了函数自变量的取值范围问题,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
9.0和1
【分析】
观察本题形式,用因式分解法比较简单,在移项提取后,左边将变成两个式子相乘为0的情况,让每个式子分别为0,即可求出.
【详解】
移项得:,
即,
解得:.
故答案为:和 .
【点睛】
本题考查了因式分解法解一元二次方程,因式分解法是解一元二次方程的一种简便方法,要会灵活运用.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.
10.且.
【分析】
根据根的判别式及一元二次方程的定义解题即可.
【详解】
∵关于x的一元二次方程有两个不相等的实数根,
,
解得.
又∵该方程为一元二次方程,
,
且.
故答案为:且.
【点睛】
本题主要考查根的判别式及一元二次方程的定义,属于基础题,掌握根的判别式及一元二次方程的定义是解题的关键.
11.
【分析】
首先根据求出方程的两个根,然后即可分解因式.
【详解】
令,
∴,
,
故答案为:.
【点睛】
本题主要考查因式分解,根据方程求出两个解是关键.
12.等腰直角三角形.
【分析】
根据题意作出,然后根据图形,得到,,可判断的形状.
【详解】
解:∵各点坐标分别是,和 ,根据题意,如下图所示
则:,, ,
∴,,
∴的形状是等腰直角三角形,
故答案是:等腰直角三角形.
【点睛】
本题考查的是勾股定理、坐标与图形性质,熟悉相关性质是解题的关键.
13.
【分析】
根据反比例函数的性质得出反比例函数的图象在每一个象限内y随着x的增大而减小,从而可确定答案.
【详解】
,
反比例函数的图象在每一个象限内y随着x的增大而减小,
,
,
故答案为:.
【点睛】
本题主要考查反比例函数的性质,掌握反比例函数的性质是关键.
14.
【分析】
把x=5代入计算即可.
【详解】
解:把x=5代入,得
.
故答案为:.
【点睛】
本题考查了求函数值,以及分母有理化,分母有理化的方法则是把分子、分母同乘以分母的有理化因式,因此分母有理化的关键是找分母的有理化因式.
15.4
【分析】
分析:根据角平分线上的点到角的两边的距离相等作出图形即可得解.
【详解】
如图所示,
加油站站的地址有四处.
故选D.
【点睛】
考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并是解题的关键,作出图形更形象直观.
16.
【分析】
根据“,”可知∠B=60°,根据“以直角顶点为圆心,长为半径画弧交于点”可知△ABD是等边三角形,∠BAD=60°,继而可知∠DAE=30°,利用直角三角中30°所对的边是斜边的一半,即可知AB和BC的长,再利用勾股定理即可求出AC的长,从而可得周长.
【详解】
∵中,,
∴∠B=60°,BC=2AB
∵以直角顶点为圆心,长为半径画弧交于点,
∴AB=AD
∵∠B=60°
∴△ABD是等边三角形
∴∠BAD=60°,
∴∠DAE=30°,
又∵DE⊥AC
∴△ADE是直角三角形
∴AD=2DE=2a
∴AB=2a,BC=4a
根据勾股定理有
∴
∴△ABC的周长=AB+AC+BC=
故答案为.
【点睛】
本题考查的是含有30°角的直角三角形和勾股定理,能够根据含有30°角的直角三角形相关性质和勾股定理求出三边的长是解题的关键.
17..
【分析】
根据题意作出图形,然后根据角平分线的性质得到,再根据三角形的面积和最小角割比Ω的定义计算即可.
【详解】
解:如图示,,,,
则,根据题意,作的角平分线交于点,
过点,作交于点,
过点,作交于点,
则
∵,,
则()
故答案是:.
【点睛】
本题考查了三角形角平分线的性质和三角形的面积计算,熟悉相关性质是解题的关键.
18.或.
【分析】
根据中,,可知是等腰直角三角形,,再根据顺时针旋转,或逆时针旋转两种情况,进行作图分析讨论,然后得到结果.
【详解】
解:在中,,
∴是等腰直角三角形,
∴,
①如下图示,当顺时针绕点C旋转得到时,
∵,则有,
∴是等边三角形,
∴
∴;
②如下图示,当逆时针绕点C旋转得到时,
∵,则有,
∴是等边三角形,
∴
∴;
综上所述,的度数是:或,
故答案是:或.
【点睛】
本题考查了旋转的性质、等腰直角三角形的判定与性质、等边三角形的判定和性质、外角的性质等知识点,熟练掌握旋转的性质,并能进行分类讨论是解决问题的关键.
19.
【分析】
先将各项分别化简,再合并同类二次根式.
【详解】
解:
=
=
【点睛】
本题考查了二次根式的混合运算,解题的关键是掌握运算法则以及二次根式的性质.
20.x1=1+,x2=1-
【分析】
方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形后,开方即可求出解.
【详解】
解:方程变形得:x2-2x=-
配方得:x2-2x+1=
即(x-1)2=,
开方得:x-1=±,
解得:x1=1+,x2=1-
考点:解一元二次方程-配方法.
21.10%
【分析】
首先求出2月份口罩的产量,然后设该口罩厂这两个月口罩生产数量的月平均增长率为x,然后根据题意列出方程就,解方程即可.
【详解】
(万个),
∴2月份口罩的产量为50万个,
设该口罩厂这两个月口罩生产数量的月平均增长率为x,根据题意得,
,
解得或(舍去),
∴该口罩厂这两个月口罩生产数量的月平均增长率为10%.
【点睛】
本题主要考查一元二次方程的应用,读懂题意列出方程是关键.
22.(1)见解析;(2)9厘米
【分析】
(1)根据线段垂直平分线的性质可知点E在线段AC的垂直平分线上,又因为点E在AB边上,从而可确定点E的位置;
(2)过点C作交AB于点D,首先根据等腰三角形三线合一得出,进而得出,然后利用含30°的直角三角形的性质求解即可.
【详解】
(1)如图:
(2)过点C作交AB于点D,
,
,
.
,
,
,
.
【点睛】
本题主要考查作垂直平分线,等腰三角形三线合一,含30°的直角三角形的性质,掌握这些性质是解题的关键.
23.(1)3000 (2)10 15 200 (3)y=120x,0≤x≤25
【分析】
(1)根据函数图象中的数据可以直接写出图书馆到小燕家的距离;
(2)根据题意和函数图象中的数据可以得到a、b、m的值;
(3)根据函数图象中的数据可以得到妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式以及定义域.
【详解】
(1)由图象可得,
图书馆到小燕家的距离是3000米,
故答案为3000;
(2)a=1500÷150=10,
b=a+5=10+5=15,
m=(3000-1500)÷(22.5-15)=200,
故答案为10,15,200;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是y=kx,
当y=3000时,x=3000÷120=25,
则3000=25k,得k=120,
即妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是y=120x,定义域是0≤x≤25,
故答案为y=120x,0≤x≤25.
【点睛】
此题考查一次函数的应用,解题关键是明确题意,利用一次函数的性质和数形结合的思想解答.
24.(1);(2)证明过程见解析
【分析】
(1)根据已知条件证明△ADE是等边三角形,即可得解;
(2)以E为圆心,DE为半径画圆,根据圆周角定理判断即可;
【详解】
(1)∵,
又∵E为中点,△ABD和△ABC都是直角三角形,
∴,
∴△ADE是等边三角形,
∴,
∴;
(2)以E为圆心,DE为半径画圆,如图所示,
∵E为AB的中点,△ABD和△ABC都是直角三角形,
∴,即B,C,D都在圆上,
又∵是圆心角,为圆周角,
∴;
【点睛】
本题主要考查了直角三角形的性质、等边三角形的性质和圆周角定理,准确计算是解题的关键.
25.(1);(2)(18,12)或
【分析】
(1)利用待定系数法求得反比例函数和射线OA的解析式,然后结合函数图像上点的坐标特点求得B点和D点坐标,然后结合勾股定理求得AD的长;
(2)设B点坐标为(x,),D点坐标为(x,),结合三角形面积公式列方程求解
【详解】
解:(1)将点代入反比例函数中,
∴反比例函数解析式为:
设射线OA的解析式为:
将点代入中,,解得:
∴射线OA的解析式为:
在中,当x=6时,y=4
∴B点坐标为(6,4)
在中,当x=6时,y=1
∴D点坐标为(6,1)
过点A作AE⊥BC
∵,B(6,4),D(6,1)
∴AE=3,DE=1
在Rt△ADE中,
(2)设B点坐标为(x,),
∴D点坐标为(x,)
∴
解得:;
∴B点坐标为(18,12)或
【点睛】
本题考查了正比例函数的图象和性质、反比例函数的图象和性质,将点的坐标转化为线段的长,利用方程求出所设的参数,进而求出结果是解决此类问题常用的方法.
26.(1)见解析;(2)图见解析,2;(3)
【分析】
(1)先判断出,进而判断出,再判断出,得到即可;
(2)依题意画出图形,由(1)得到,再判断出,求出,进而求出AE;
(3)先表示出,再判断出,得到,在中,,即,即可.
【详解】
(1)证明:如图1,
作于点H,作于点F,
,
.
,
.
,即,
.
,
.
,
,
,
,
,
;
(2)如图2,
作于点H,作于点F,
同(1)得,
,
,
,
.
,
.
,
.
,
,
,
.
∵在四边形AHPF中,,
∴四边形AHPF是矩形,
,
;
(3)如图3,
作于点H,作于点F,
由(2)得,
,
,
,
,
.
∵PG平分,
.
,
,
,
在中,,
即,
.
【点睛】
本题主要考查全等三角形的性质和判定,矩形的判定及性质,同角的余角相等,勾股定理,证明出是关键.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.下列关于x的方程一定有实数根的是( )
A. B. C. D.
4.学校升旗仪式上,徐徐上升的国旗的高度与时间的关系可以用下面的一个函数图像近似地刻画,这个函数图像是( )
A. B.
C. D.
5.下列定理有逆定理的是( )
A.对顶角相等 B.直角三角形两锐角互余
C.全等三角形的对应角相等 D.全等三角形的面积相等
6.如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,以下判断中正确的个数有( )
①∠DCB=∠A;②∠DCB=∠ACE;③∠ACD=∠BCE;④∠BCE=∠BEC.
A.1个 B.2个 C.3个 D.4个
二、填空题
7.计算: =_____.
8.函数的定义域是_____.
9.方程的根是____________.
10.关于x的一元二次方程有两个不相等的实数根,则k的取值范围是________.
11.在实数范围内分解因式:______.
12.已知直角坐标平面内的点,和,那么的形状是______.
13.已知反比例函数的图像上有两点,,那么______.(填“>”或“<”)
14.已知函数,那么______.
15.随着人们生活水平的不断提高,汽车逐步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有_______处.
16.如图.在中,,,以直角顶点为圆心,长为半径画弧交于点,过点作于点,若,则的周长用含的代数式表示为_______________.
17.我们定义:一个三角形最小内角的角平分线将这个三角形分割得到的两个三角形它们的面积之比称为“最小角割比Ω”(),那么三边长分别为7,24,25的三角形的最小角割比Ω是______.
18.在中,,,将绕点C旋转得到,点A,B分别与,对应,当时,记直线与直线交点为E,那么 的度数是______.
三、解答题
19.计算:
20.解方程:
21.某口罩厂2020年1月口罩生产数量40万个,2月份口罩产量增长了25%,为应对“新冠”疫情,计划通过两个月进行产能爬坡,预计到4月份时月产量达到60.5万个,求该口罩厂这两个月口罩生产数量的月平均增长率.
22.如图,中,,.
(1)利用直尺,圆规在边上找一点E,使得;(不需要写作法,但要保留作图痕迹)
(2)若厘米,求的长.
23.为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度到达图书馆,而妈妈始终以120米/分钟的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图像,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2)a= ,b= ,m= ;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是 ;定义域是 .
24.如图,在中,,F为上一点,作交延长线于点D,E为中点,分别联结,.
(1)当时,求的度数;
(2)求证:.
25.如图,在平面直角坐标系中,点在反比例函数的图像上,点B在射线上,轴,垂足为C,与反比例函数的图像相交于点D,连接,.
(1)当点B的横坐标为6时,求线段的长;
(2)若,求点的坐标.
26.如图,已知,直线,点P在线段上,点D为射线上一动点,连接,射线交直线于点E.已知,.
(1)如图1,当点D在线段上时,求证:;
(2)当时,请在图2中画出相应的图形,并求线段的长;
(3)如果的平分线交射线于点G,设,,求y关于x的函数关系式,并写出自变量x的取值范围.
参考答案
1.D
【分析】
根据二次根式的性质把各个二次根式化简,根据同类二次根式的概念判断即可.
【详解】
解:A、,与不是同类二次根式;
B、,与不是同类二次根式;
C、,与不是同类二次根式;
D、,与是同类二次根式;
故选:D.
【点睛】
本题考查的是同类二次根式的概念、二次根式的化简,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式.
2.D
【分析】
根据二次根式的加减法、乘除法法则和算术平方根的意义分别判断.
【详解】
解:A、无法合并计算,故错误;
B、,故错误;
C、,故错误;
D、,故正确.
故选D.
【点睛】
本题考查了二次根式的运算,解题的关键是掌握运算法则.
3.A
【分析】
分别根据方程的解得定义,从a的取值出发进行判断.
【详解】
解:A、有实数解,故符合;
B、,当a=0时,等式不成立,即方程无实数解,故不符合;
C、,当a=0时,等式不成立,即方程无实数解,故不符合;
D、,当a<0时,等式不成立,即方程无实数解,故不符合;
故选A.
【点睛】
本题考查了方程的解,解题的关键是理解方程的解的定义,对a值进行取值验证.
4.B
【分析】
根据国旗上升的高度随着时间的增长而逐渐变大可得出答案.
【详解】
国旗上升的高度随着时间的增长而逐渐变大,可知图象如B选项,
故选:B.
【点睛】
本题主要考查函数的图象,掌握生活常识是关键.
5.B
【分析】
先分别写出第个选项的逆命题,再判断其是否正确.
【详解】
解:A的逆命题是:相等的角是对顶角,假命题;
B的逆命题是:两锐角互余的三角形是直角三角形,真命题;
C的逆命题是:面积相等的三角形是全等三角形,假命题;
D的逆命题是:对应角相等的三角形是全等三角形,假命题;
故选:B.
【点睛】
本题主要考查了学生对逆命题以及真假命题的定义的理解,要求学生对常用的基础知识牢固掌握,比较简单.
6.C
【分析】
根据垂直的定义得到∠CDB=90°,根据余角的性质得到∠DCB=∠A,故①正确;根据直角三角形的性质得到AE=CE=BE,根据等腰三角形的性质得到∠A=∠ACE,于是得到∠DCB=∠ACE,故②正确;同理得到∠ACD=∠BCE,故③正确;由于BC不一定等于BE,于是得到∠BCE不一定等于∠BEC,故④错误.
【详解】
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB+B=90°,
∵∠A+∠B=90,
∴∠DCB=∠A,
∴①正确;
∵CE是RtABC斜边AB上的中线,
∴EA=EC=EB,
∴∠ACE=∠A,
∴∠DCB=∠A,
∴∠DCB=∠ACE,
∴②正确;
∵EC=EB,
∴∠B=∠BCE,
∵∠A+∠B=90,∠A+∠ACD=90,
∴∠B= ∠ACD,
∴∠ACD= ∠BCE,
∴③正确;
∵BC与BE不一定相等,
∴∠BCE 与∠BEC 不一定相等,
∴④不正确;
∴正确的个数为3个,
故答案为C.
【点睛】
本题考查了直角三角形的性质,熟练掌握直角三角形的性质是解题的关键.
7.
【分析】
根据立方根的意义求解即可.
【详解】
.
8.x≥.
【分析】
根据二次根式有意义的条件:被开方数大于或等于0,即可求出x的范围.
【详解】
解:根据题意得:2x﹣1≥0,解得:x≥.
故答案为x≥.
【点睛】
本题考查了函数自变量的取值范围问题,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
9.0和1
【分析】
观察本题形式,用因式分解法比较简单,在移项提取后,左边将变成两个式子相乘为0的情况,让每个式子分别为0,即可求出.
【详解】
移项得:,
即,
解得:.
故答案为:和 .
【点睛】
本题考查了因式分解法解一元二次方程,因式分解法是解一元二次方程的一种简便方法,要会灵活运用.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.
10.且.
【分析】
根据根的判别式及一元二次方程的定义解题即可.
【详解】
∵关于x的一元二次方程有两个不相等的实数根,
,
解得.
又∵该方程为一元二次方程,
,
且.
故答案为:且.
【点睛】
本题主要考查根的判别式及一元二次方程的定义,属于基础题,掌握根的判别式及一元二次方程的定义是解题的关键.
11.
【分析】
首先根据求出方程的两个根,然后即可分解因式.
【详解】
令,
∴,
,
故答案为:.
【点睛】
本题主要考查因式分解,根据方程求出两个解是关键.
12.等腰直角三角形.
【分析】
根据题意作出,然后根据图形,得到,,可判断的形状.
【详解】
解:∵各点坐标分别是,和 ,根据题意,如下图所示
则:,, ,
∴,,
∴的形状是等腰直角三角形,
故答案是:等腰直角三角形.
【点睛】
本题考查的是勾股定理、坐标与图形性质,熟悉相关性质是解题的关键.
13.
【分析】
根据反比例函数的性质得出反比例函数的图象在每一个象限内y随着x的增大而减小,从而可确定答案.
【详解】
,
反比例函数的图象在每一个象限内y随着x的增大而减小,
,
,
故答案为:.
【点睛】
本题主要考查反比例函数的性质,掌握反比例函数的性质是关键.
14.
【分析】
把x=5代入计算即可.
【详解】
解:把x=5代入,得
.
故答案为:.
【点睛】
本题考查了求函数值,以及分母有理化,分母有理化的方法则是把分子、分母同乘以分母的有理化因式,因此分母有理化的关键是找分母的有理化因式.
15.4
【分析】
分析:根据角平分线上的点到角的两边的距离相等作出图形即可得解.
【详解】
如图所示,
加油站站的地址有四处.
故选D.
【点睛】
考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并是解题的关键,作出图形更形象直观.
16.
【分析】
根据“,”可知∠B=60°,根据“以直角顶点为圆心,长为半径画弧交于点”可知△ABD是等边三角形,∠BAD=60°,继而可知∠DAE=30°,利用直角三角中30°所对的边是斜边的一半,即可知AB和BC的长,再利用勾股定理即可求出AC的长,从而可得周长.
【详解】
∵中,,
∴∠B=60°,BC=2AB
∵以直角顶点为圆心,长为半径画弧交于点,
∴AB=AD
∵∠B=60°
∴△ABD是等边三角形
∴∠BAD=60°,
∴∠DAE=30°,
又∵DE⊥AC
∴△ADE是直角三角形
∴AD=2DE=2a
∴AB=2a,BC=4a
根据勾股定理有
∴
∴△ABC的周长=AB+AC+BC=
故答案为.
【点睛】
本题考查的是含有30°角的直角三角形和勾股定理,能够根据含有30°角的直角三角形相关性质和勾股定理求出三边的长是解题的关键.
17..
【分析】
根据题意作出图形,然后根据角平分线的性质得到,再根据三角形的面积和最小角割比Ω的定义计算即可.
【详解】
解:如图示,,,,
则,根据题意,作的角平分线交于点,
过点,作交于点,
过点,作交于点,
则
∵,,
则()
故答案是:.
【点睛】
本题考查了三角形角平分线的性质和三角形的面积计算,熟悉相关性质是解题的关键.
18.或.
【分析】
根据中,,可知是等腰直角三角形,,再根据顺时针旋转,或逆时针旋转两种情况,进行作图分析讨论,然后得到结果.
【详解】
解:在中,,
∴是等腰直角三角形,
∴,
①如下图示,当顺时针绕点C旋转得到时,
∵,则有,
∴是等边三角形,
∴
∴;
②如下图示,当逆时针绕点C旋转得到时,
∵,则有,
∴是等边三角形,
∴
∴;
综上所述,的度数是:或,
故答案是:或.
【点睛】
本题考查了旋转的性质、等腰直角三角形的判定与性质、等边三角形的判定和性质、外角的性质等知识点,熟练掌握旋转的性质,并能进行分类讨论是解决问题的关键.
19.
【分析】
先将各项分别化简,再合并同类二次根式.
【详解】
解:
=
=
【点睛】
本题考查了二次根式的混合运算,解题的关键是掌握运算法则以及二次根式的性质.
20.x1=1+,x2=1-
【分析】
方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形后,开方即可求出解.
【详解】
解:方程变形得:x2-2x=-
配方得:x2-2x+1=
即(x-1)2=,
开方得:x-1=±,
解得:x1=1+,x2=1-
考点:解一元二次方程-配方法.
21.10%
【分析】
首先求出2月份口罩的产量,然后设该口罩厂这两个月口罩生产数量的月平均增长率为x,然后根据题意列出方程就,解方程即可.
【详解】
(万个),
∴2月份口罩的产量为50万个,
设该口罩厂这两个月口罩生产数量的月平均增长率为x,根据题意得,
,
解得或(舍去),
∴该口罩厂这两个月口罩生产数量的月平均增长率为10%.
【点睛】
本题主要考查一元二次方程的应用,读懂题意列出方程是关键.
22.(1)见解析;(2)9厘米
【分析】
(1)根据线段垂直平分线的性质可知点E在线段AC的垂直平分线上,又因为点E在AB边上,从而可确定点E的位置;
(2)过点C作交AB于点D,首先根据等腰三角形三线合一得出,进而得出,然后利用含30°的直角三角形的性质求解即可.
【详解】
(1)如图:
(2)过点C作交AB于点D,
,
,
.
,
,
,
.
【点睛】
本题主要考查作垂直平分线,等腰三角形三线合一,含30°的直角三角形的性质,掌握这些性质是解题的关键.
23.(1)3000 (2)10 15 200 (3)y=120x,0≤x≤25
【分析】
(1)根据函数图象中的数据可以直接写出图书馆到小燕家的距离;
(2)根据题意和函数图象中的数据可以得到a、b、m的值;
(3)根据函数图象中的数据可以得到妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式以及定义域.
【详解】
(1)由图象可得,
图书馆到小燕家的距离是3000米,
故答案为3000;
(2)a=1500÷150=10,
b=a+5=10+5=15,
m=(3000-1500)÷(22.5-15)=200,
故答案为10,15,200;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是y=kx,
当y=3000时,x=3000÷120=25,
则3000=25k,得k=120,
即妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是y=120x,定义域是0≤x≤25,
故答案为y=120x,0≤x≤25.
【点睛】
此题考查一次函数的应用,解题关键是明确题意,利用一次函数的性质和数形结合的思想解答.
24.(1);(2)证明过程见解析
【分析】
(1)根据已知条件证明△ADE是等边三角形,即可得解;
(2)以E为圆心,DE为半径画圆,根据圆周角定理判断即可;
【详解】
(1)∵,
又∵E为中点,△ABD和△ABC都是直角三角形,
∴,
∴△ADE是等边三角形,
∴,
∴;
(2)以E为圆心,DE为半径画圆,如图所示,
∵E为AB的中点,△ABD和△ABC都是直角三角形,
∴,即B,C,D都在圆上,
又∵是圆心角,为圆周角,
∴;
【点睛】
本题主要考查了直角三角形的性质、等边三角形的性质和圆周角定理,准确计算是解题的关键.
25.(1);(2)(18,12)或
【分析】
(1)利用待定系数法求得反比例函数和射线OA的解析式,然后结合函数图像上点的坐标特点求得B点和D点坐标,然后结合勾股定理求得AD的长;
(2)设B点坐标为(x,),D点坐标为(x,),结合三角形面积公式列方程求解
【详解】
解:(1)将点代入反比例函数中,
∴反比例函数解析式为:
设射线OA的解析式为:
将点代入中,,解得:
∴射线OA的解析式为:
在中,当x=6时,y=4
∴B点坐标为(6,4)
在中,当x=6时,y=1
∴D点坐标为(6,1)
过点A作AE⊥BC
∵,B(6,4),D(6,1)
∴AE=3,DE=1
在Rt△ADE中,
(2)设B点坐标为(x,),
∴D点坐标为(x,)
∴
解得:;
∴B点坐标为(18,12)或
【点睛】
本题考查了正比例函数的图象和性质、反比例函数的图象和性质,将点的坐标转化为线段的长,利用方程求出所设的参数,进而求出结果是解决此类问题常用的方法.
26.(1)见解析;(2)图见解析,2;(3)
【分析】
(1)先判断出,进而判断出,再判断出,得到即可;
(2)依题意画出图形,由(1)得到,再判断出,求出,进而求出AE;
(3)先表示出,再判断出,得到,在中,,即,即可.
【详解】
(1)证明:如图1,
作于点H,作于点F,
,
.
,
.
,即,
.
,
.
,
,
,
,
,
;
(2)如图2,
作于点H,作于点F,
同(1)得,
,
,
,
.
,
.
,
.
,
,
,
.
∵在四边形AHPF中,,
∴四边形AHPF是矩形,
,
;
(3)如图3,
作于点H,作于点F,
由(2)得,
,
,
,
,
.
∵PG平分,
.
,
,
,
在中,,
即,
.
【点睛】
本题主要考查全等三角形的性质和判定,矩形的判定及性质,同角的余角相等,勾股定理,证明出是关键.
同课章节目录
