2020—2021学年八年级数学沪科版下册第18章《勾股定理》培优试题(word版含答案)
文档属性
| 名称 | 2020—2021学年八年级数学沪科版下册第18章《勾股定理》培优试题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览


文档简介
2020—2021学年八年级数学沪科版下册第18章《勾股定理》培优试题与简答
一.选择题(共10小题,每小题2分,共20分)
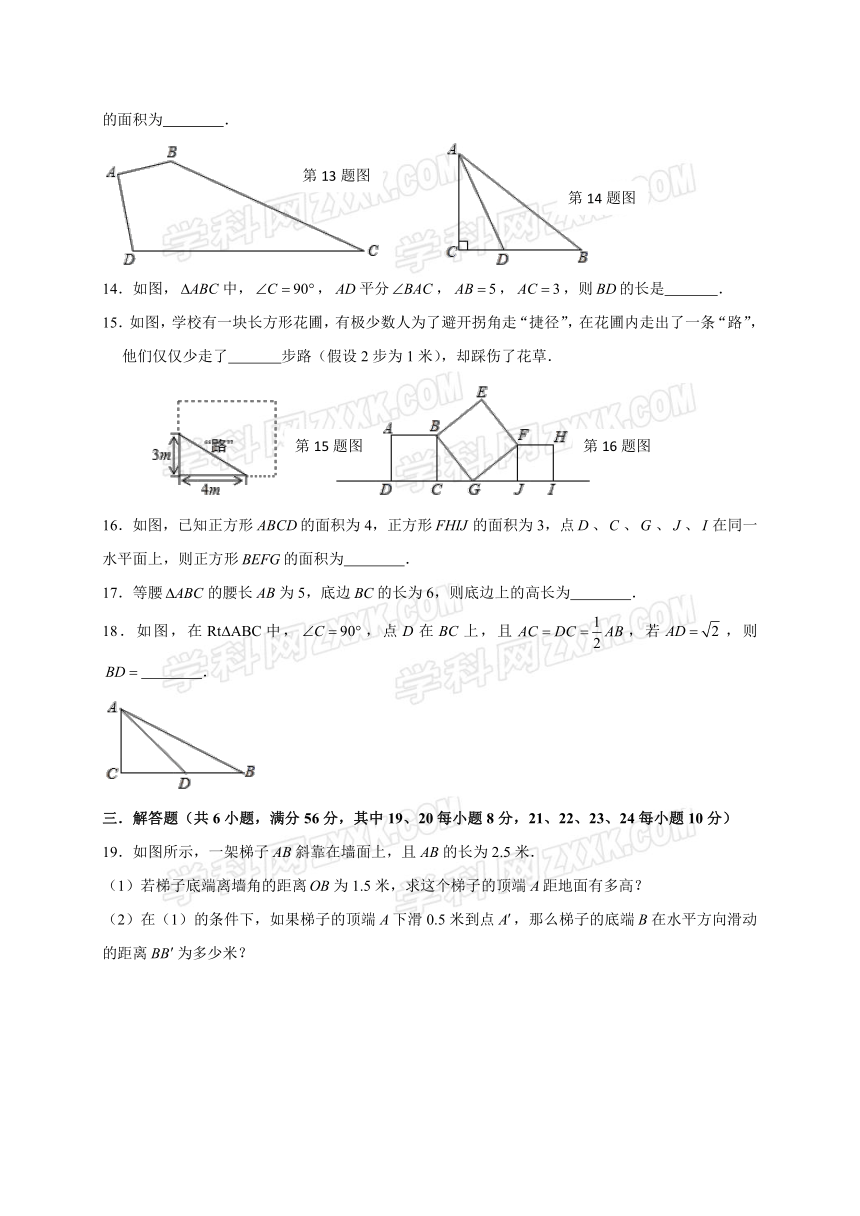
1.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形的面积为
A.6
B.36
C.64
D.8
2.下列各组数中,是勾股数的为
A.1,1,2
B.1.5,2,2.5
C.7,24,25
D.6,12,13
3.如图,,,三点在边长为1的正方形网格的格点上,则的度数为
A.
B.
C.
D.
4.若一直角三角形的两边长分别是6,8,则第三边长为
A.10
B.
C.10或
D.14
5.如图,是一种饮料的包装盒,长、宽、高分别为、、,现有一长为的吸管插入到盒的底部,则吸管露在盒外的部分的取值范围为
A.
B.
C.
D.
6.已知、、是三角形的三边长,如果满足,则三角形的形状是
A.直角三角形
B.等边三角形
C.钝角三角形
D.底与腰不相等的等腰三角形
7.如图,轴、轴上分别有两点、,以点为圆心,为半径的弧交轴负半轴于点,则点的坐标为
A.
B.,
C.,
D.,
8.已知的周长是,斜边上的中线长是2,则为
A.16
B.8
C.4
D.12
9.如图,在中,,沿折叠,使点恰好落在边上点处,若,则的大小为
A.
B.
C.
D.
10.在如图的网格中,小正方形的边长均为1,、、三点均在正方形格点上,则下列结论错误的是
A.
B.
C.
D.点到直线的距离是2
二.填空题(共8小题,每小题3分,共24分)
11.已知直角三角形的长为、,则第三边长为
.
12.如图,一只蚂蚁沿着边长为2的正方体表面从顶点出发,经过3个面爬到顶点,如果它运动的路径是最短的,则最短路径为
.
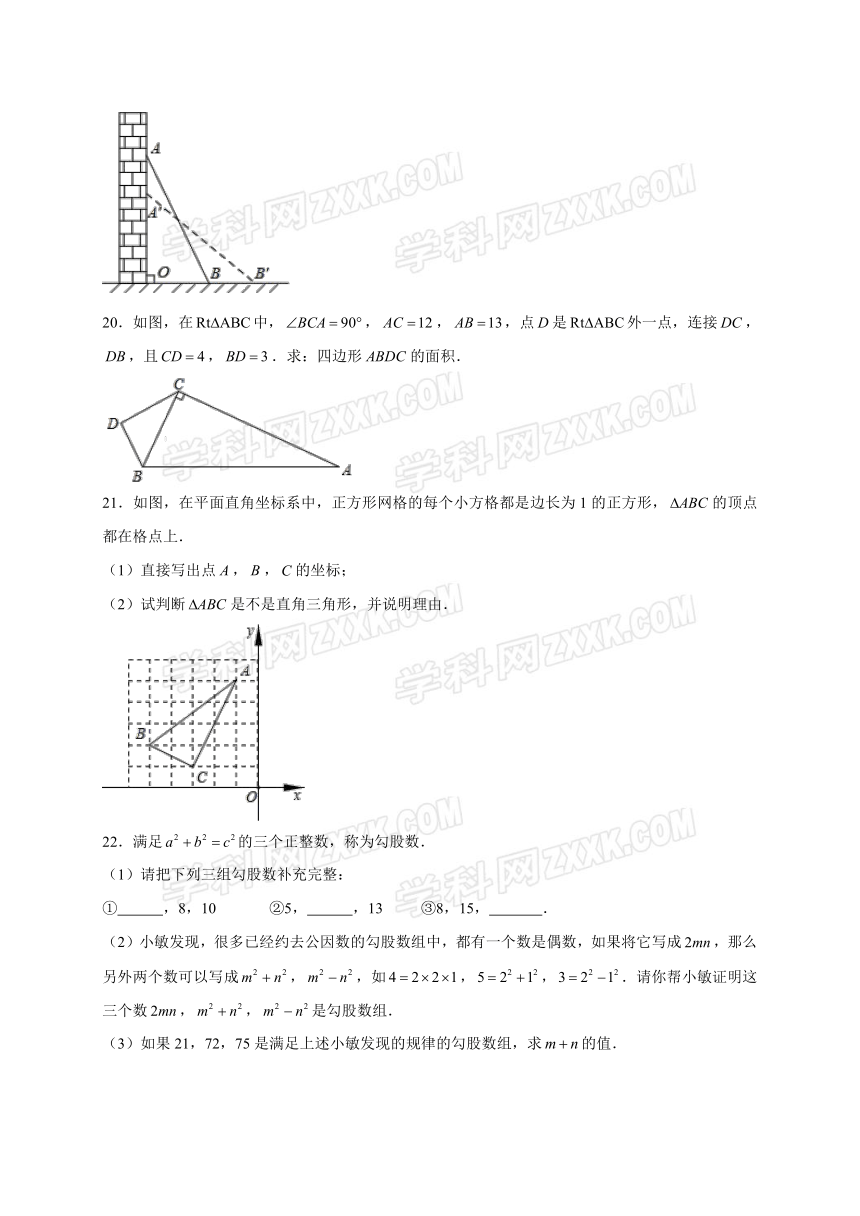
13.如图,有一四边形空地,,,,,,则四边形的面积为
.
14.如图,中,,平分,,,则的长是
.
15.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了
步路(假设2步为1米),却踩伤了花草.
16.如图,已知正方形的面积为4,正方形的面积为3,点、、、、在同一水平面上,则正方形的面积为
.
17.等腰的腰长为5,底边的长为6,则底边上的高长为
.
18.如图,在中,,点在上,且,若,则
.
三.解答题(共6小题,满分56分,其中19、20每小题8分,21、22、23、24每小题10分)
19.如图所示,一架梯子斜靠在墙面上,且的长为2.5米.
(1)若梯子底端离墙角的距离为1.5米,求这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑0.5米到点,那么梯子的底端在水平方向滑动的距离为多少米?
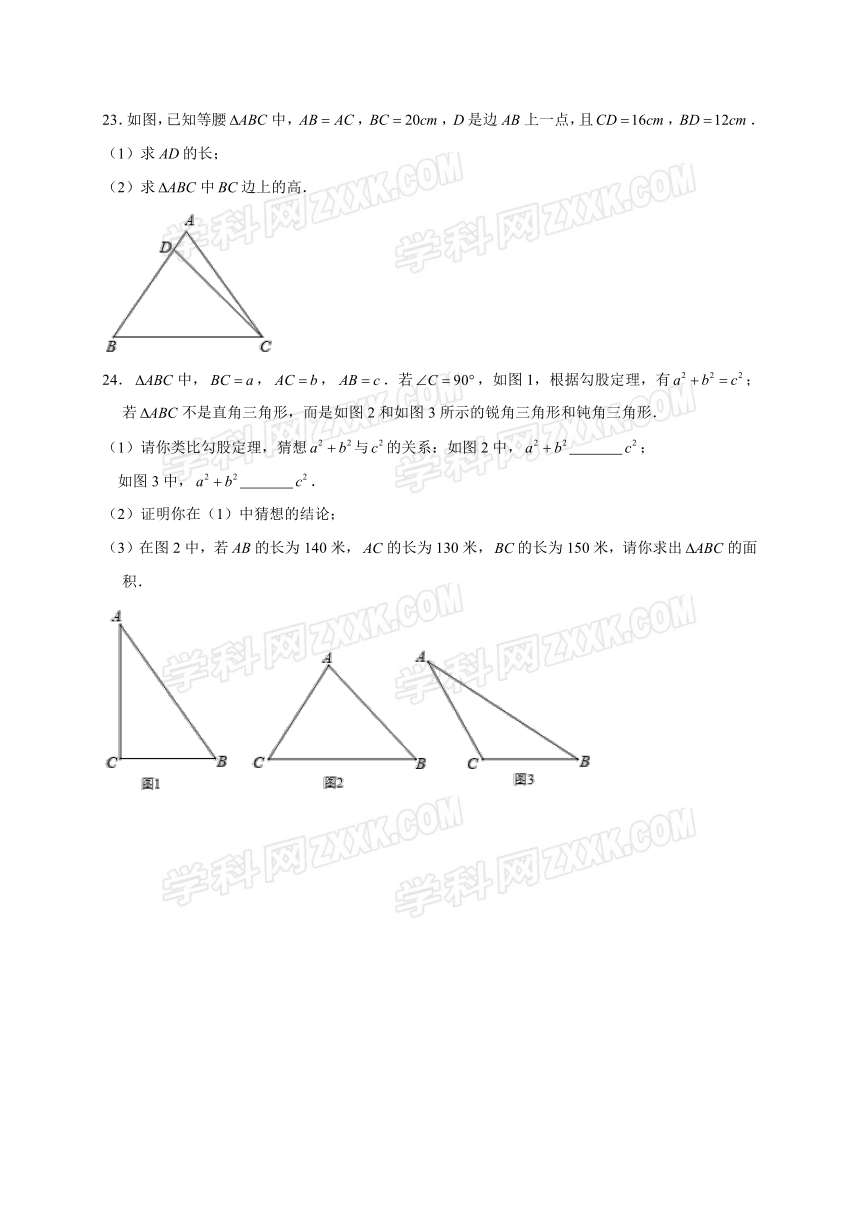
20.如图,在中,,,,点是外一点,连接,,且,.求:四边形的面积.
21.如图,在平面直角坐标系中,正方形网格的每个小方格都是边长为1的正方形,的顶点都在格点上.
(1)直接写出点,,的坐标;
(2)试判断是不是直角三角形,并说明理由.
22.满足的三个正整数,称为勾股数.
(1)请把下列三组勾股数补充完整:
①
,8,10
②5,
,13
③8,15,
.
(2)小敏发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成,那么另外两个数可以写成,,如,,.请你帮小敏证明这三个数,,是勾股数组.
(3)如果21,72,75是满足上述小敏发现的规律的勾股数组,求的值.
23.如图,已知等腰中,,,是边上一点,且,.
(1)求的长;
(2)求中边上的高.
24.中,,,.若,如图1,根据勾股定理,有;若不是直角三角形,而是如图2和如图3所示的锐角三角形和钝角三角形.
(1)请你类比勾股定理,猜想与的关系:如图2中,
;
如图3中,
.
(2)证明你在(1)中猜想的结论;
(3)在图2中,若的长为140米,的长为130米,的长为150米,请你求出的面积.
2020—2021学年八年级数学沪科版下册第18章《勾股定理》培优试题参考简答
一.选择题(共10小题)
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
二.填空题(共8小题)
11. 或4 .
12. .
13. 36 .
14. 2.5 .
15. 4 .
16. 7 .
17. 4 .
18. .
三.解答题(共6小题)
19.如图所示,一架梯子斜靠在墙面上,且的长为2.5米.
(1)若梯子底端离墙角的距离为1.5米,求这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑0.5米到点,那么梯子的底端在水平方向滑动的距离为多少米?
【解】:(1)根据勾股定理:
所以梯子距离地面的高度为:米;
(2)梯子下滑了0.5米即梯子距离地面的高度为米,
根据勾股定理:米,
所以当梯子的顶端下滑0.5米时,梯子的底端水平后移了米,
答:当梯子的顶端下滑0.5米时,梯子的底端水平后移了0.5米.
20.如图,在中,,,,点是外一点,连接,,且,.求:四边形的面积.
【解】:中,,,,
;
在中,,,,
,
是直角三角形,
四边形的面积.
21.如图,在平面直角坐标系中,正方形网格的每个小方格都是边长为1的正方形,的顶点都在格点上.
(1)直接写出点,,的坐标;
(2)试判断是不是直角三角形,并说明理由.
【解】:(1),,;
(2)是直角三角形.
证明:,
,
,
.
由勾股定理的逆定理可知,是直角三角形,.
22.满足的三个正整数,称为勾股数.
(1)请把下列三组勾股数补充完整:
①
,8,10
②5,
,13
③8,15,
.
(2)小敏发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成,那么另外两个数可以写成,,如,,.请你帮小敏证明这三个数,,是勾股数组.
(3)如果21,72,75是满足上述小敏发现的规律的勾股数组,求的值.
【解】:(1)①6,8,10;
②5,12,13;③8,15,17.
(2)证明:,
,
,
,,是勾股数;
(3)化简得:7,24,25,
偶数,,,
,,
.
23.如图,已知等腰中,,,是边上一点,且,.
(1)求的长;
(2)求中边上的高.
【解】:(1),且,,
,
,
,
设,则,
在中,由勾股定理得:,
即,
解得:,
即;
(2),
过作于,则是的高,
,,
,
在中,由勾股定理得:,
即中边上的高是.
24.中,,,.若,如图1,根据勾股定理,有;若不是直角三角形,而是如图2和如图3所示的锐角三角形和钝角三角形.
(1)请你类比勾股定理,猜想与的关系:如图2中,
;
如图3中,
.
(2)证明你在(1)中猜想的结论;
(3)在图2中,若的长为140米,的长为130米,的长为150米,请你求出的面积.
【解】:(1)如图2中,;如图3中,.
(2)如图2,作边上的高,
在直角三角形和中,设,
则:,
整理得:
,
.
如图3,作边上的高,
在直角三角形中中,设,
则:
整理得:
,
.
(3)如图2,设米,则米,
在中,由勾股定理,得
在中,由勾股定理,得,
所以,
即,
解得.
所以,
则(取正值)
所以,所求的面积为(米.
故的面积是8400米.
第5题图
第3题图
第1题图
第10题图
第9题图
第14题图
第13题图
第16题图
第15题图
一.选择题(共10小题,每小题2分,共20分)
1.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形的面积为
A.6
B.36
C.64
D.8
2.下列各组数中,是勾股数的为
A.1,1,2
B.1.5,2,2.5
C.7,24,25
D.6,12,13
3.如图,,,三点在边长为1的正方形网格的格点上,则的度数为
A.
B.
C.
D.
4.若一直角三角形的两边长分别是6,8,则第三边长为
A.10
B.
C.10或
D.14
5.如图,是一种饮料的包装盒,长、宽、高分别为、、,现有一长为的吸管插入到盒的底部,则吸管露在盒外的部分的取值范围为
A.
B.
C.
D.
6.已知、、是三角形的三边长,如果满足,则三角形的形状是
A.直角三角形
B.等边三角形
C.钝角三角形
D.底与腰不相等的等腰三角形
7.如图,轴、轴上分别有两点、,以点为圆心,为半径的弧交轴负半轴于点,则点的坐标为
A.
B.,
C.,
D.,
8.已知的周长是,斜边上的中线长是2,则为
A.16
B.8
C.4
D.12
9.如图,在中,,沿折叠,使点恰好落在边上点处,若,则的大小为
A.
B.
C.
D.
10.在如图的网格中,小正方形的边长均为1,、、三点均在正方形格点上,则下列结论错误的是
A.
B.
C.
D.点到直线的距离是2
二.填空题(共8小题,每小题3分,共24分)
11.已知直角三角形的长为、,则第三边长为
.
12.如图,一只蚂蚁沿着边长为2的正方体表面从顶点出发,经过3个面爬到顶点,如果它运动的路径是最短的,则最短路径为
.
13.如图,有一四边形空地,,,,,,则四边形的面积为
.
14.如图,中,,平分,,,则的长是
.
15.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了
步路(假设2步为1米),却踩伤了花草.
16.如图,已知正方形的面积为4,正方形的面积为3,点、、、、在同一水平面上,则正方形的面积为
.
17.等腰的腰长为5,底边的长为6,则底边上的高长为
.
18.如图,在中,,点在上,且,若,则
.
三.解答题(共6小题,满分56分,其中19、20每小题8分,21、22、23、24每小题10分)
19.如图所示,一架梯子斜靠在墙面上,且的长为2.5米.
(1)若梯子底端离墙角的距离为1.5米,求这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑0.5米到点,那么梯子的底端在水平方向滑动的距离为多少米?
20.如图,在中,,,,点是外一点,连接,,且,.求:四边形的面积.
21.如图,在平面直角坐标系中,正方形网格的每个小方格都是边长为1的正方形,的顶点都在格点上.
(1)直接写出点,,的坐标;
(2)试判断是不是直角三角形,并说明理由.
22.满足的三个正整数,称为勾股数.
(1)请把下列三组勾股数补充完整:
①
,8,10
②5,
,13
③8,15,
.
(2)小敏发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成,那么另外两个数可以写成,,如,,.请你帮小敏证明这三个数,,是勾股数组.
(3)如果21,72,75是满足上述小敏发现的规律的勾股数组,求的值.
23.如图,已知等腰中,,,是边上一点,且,.
(1)求的长;
(2)求中边上的高.
24.中,,,.若,如图1,根据勾股定理,有;若不是直角三角形,而是如图2和如图3所示的锐角三角形和钝角三角形.
(1)请你类比勾股定理,猜想与的关系:如图2中,
;
如图3中,
.
(2)证明你在(1)中猜想的结论;
(3)在图2中,若的长为140米,的长为130米,的长为150米,请你求出的面积.
2020—2021学年八年级数学沪科版下册第18章《勾股定理》培优试题参考简答
一.选择题(共10小题)
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
二.填空题(共8小题)
11. 或4 .
12. .
13. 36 .
14. 2.5 .
15. 4 .
16. 7 .
17. 4 .
18. .
三.解答题(共6小题)
19.如图所示,一架梯子斜靠在墙面上,且的长为2.5米.
(1)若梯子底端离墙角的距离为1.5米,求这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑0.5米到点,那么梯子的底端在水平方向滑动的距离为多少米?
【解】:(1)根据勾股定理:
所以梯子距离地面的高度为:米;
(2)梯子下滑了0.5米即梯子距离地面的高度为米,
根据勾股定理:米,
所以当梯子的顶端下滑0.5米时,梯子的底端水平后移了米,
答:当梯子的顶端下滑0.5米时,梯子的底端水平后移了0.5米.
20.如图,在中,,,,点是外一点,连接,,且,.求:四边形的面积.
【解】:中,,,,
;
在中,,,,
,
是直角三角形,
四边形的面积.
21.如图,在平面直角坐标系中,正方形网格的每个小方格都是边长为1的正方形,的顶点都在格点上.
(1)直接写出点,,的坐标;
(2)试判断是不是直角三角形,并说明理由.
【解】:(1),,;
(2)是直角三角形.
证明:,
,
,
.
由勾股定理的逆定理可知,是直角三角形,.
22.满足的三个正整数,称为勾股数.
(1)请把下列三组勾股数补充完整:
①
,8,10
②5,
,13
③8,15,
.
(2)小敏发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成,那么另外两个数可以写成,,如,,.请你帮小敏证明这三个数,,是勾股数组.
(3)如果21,72,75是满足上述小敏发现的规律的勾股数组,求的值.
【解】:(1)①6,8,10;
②5,12,13;③8,15,17.
(2)证明:,
,
,
,,是勾股数;
(3)化简得:7,24,25,
偶数,,,
,,
.
23.如图,已知等腰中,,,是边上一点,且,.
(1)求的长;
(2)求中边上的高.
【解】:(1),且,,
,
,
,
设,则,
在中,由勾股定理得:,
即,
解得:,
即;
(2),
过作于,则是的高,
,,
,
在中,由勾股定理得:,
即中边上的高是.
24.中,,,.若,如图1,根据勾股定理,有;若不是直角三角形,而是如图2和如图3所示的锐角三角形和钝角三角形.
(1)请你类比勾股定理,猜想与的关系:如图2中,
;
如图3中,
.
(2)证明你在(1)中猜想的结论;
(3)在图2中,若的长为140米,的长为130米,的长为150米,请你求出的面积.
【解】:(1)如图2中,;如图3中,.
(2)如图2,作边上的高,
在直角三角形和中,设,
则:,
整理得:
,
.
如图3,作边上的高,
在直角三角形中中,设,
则:
整理得:
,
.
(3)如图2,设米,则米,
在中,由勾股定理,得
在中,由勾股定理,得,
所以,
即,
解得.
所以,
则(取正值)
所以,所求的面积为(米.
故的面积是8400米.
第5题图
第3题图
第1题图
第10题图
第9题图
第14题图
第13题图
第16题图
第15题图
