2020-2021学年八年级数学人教版下册《第18章平行四边形》章末综合优生辅导训练(word附答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册《第18章平行四边形》章末综合优生辅导训练(word附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 331.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-09 00:00:00 | ||
图片预览




文档简介
2021年度人教版八年级数学下册《第18章平行四边形》章末综合优生辅导训练(附答案)
1.下列说法不正确的是( )
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.一个角是直角的四边形是矩形
2.如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则∠CDE的度数为( )
A.20°
B.22.5°
C.25°
D.30°
3.已知平行四边形ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为菱形的是( )
A.∠BAC=∠DCA
B.∠BAC=∠DAC
C.∠BAC=∠ABD
D.∠BAC=∠ADB
4.如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=15°,则∠COE=( )
A.45°
B.60°
C.75°
D.30°
5.如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE,AF,DE与AF交于点O.连接OC,则OC=( )
A.1
B.
C.
D.
6.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2
B.4
C.6
D.8
7.如图,正方形ABCD中,∠EAF=45°,有以下四个结论:
①BE+DF=EF;
②BM2+DN2=MN2
③若AB=3,BE=1,则BN=3;
④若CE=2,则DN=,其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
8.如图,点A、E、F、C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD.则当点E、F不重合时,BD与EF的关系是
.
9.如图平行四边形ABCD的对角线AC、BD交于一点O,点E是AD的中点,△BCD的周长为24cm,则△DEO的周长是
cm.
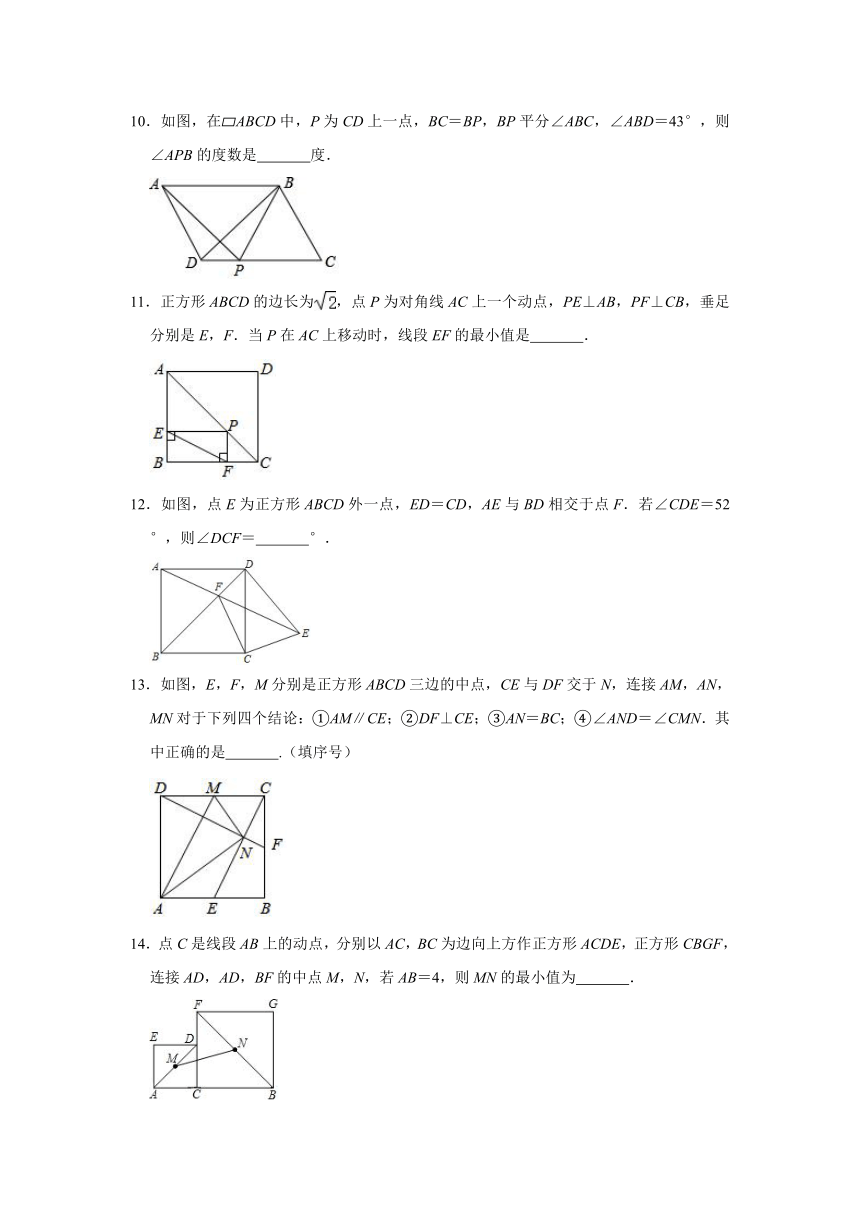
10.如图,在?ABCD中,P为CD上一点,BC=BP,BP平分∠ABC,∠ABD=43°,则∠APB的度数是
度.
11.正方形ABCD的边长为,点P为对角线AC上一个动点,PE⊥AB,PF⊥CB,垂足分别是E,F.当P在AC上移动时,线段EF的最小值是
.
12.如图,点E为正方形ABCD外一点,ED=CD,AE与BD相交于点F.若∠CDE=52°,则∠DCF=
°.
13.如图,E,F,M分别是正方形ABCD三边的中点,CE与DF交于N,连接AM,AN,MN对于下列四个结论:①AM∥CE;②DF⊥CE;③AN=BC;④∠AND=∠CMN.其中正确的是
.(填序号)
14.点C是线段AB上的动点,分别以AC,BC为边向上方作正方形ACDE,正方形CBGF,连接AD,AD,BF的中点M,N,若AB=4,则MN的最小值为
.
15.如图,在四边形ABCD中,AB∥CD,AB=CD,要使四边形ABCD为矩形,还需补充的条件可以是:
(写1个即可).
16.如图,在矩形ABCD中,AB=8,AD=6,点E,F都在CD上,点P在AD上,连接PE,若EF=PE,∠FBP=∠ABP,2∠APB+∠DPE=180°,则线段AP的长为
.
17.如图,平面直角坐标系中,四边形OABC为菱形,点A在x轴正半轴上,点A的坐标为(4,0),∠AOC=60°,对角线OB,AC相交于点E,则点E的坐标为
.
18.如图,在线段AB上取一点C,分别以AC,BC为边长作菱形BCFG和菱形ACDE,使点D在边CF上,连接EG,H是EG的中点,且CH=4,则EG的长是
.
19.如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发
秒后其中一个新四边形为平行四边形.
20.如图,在?ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
21.如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若AC=6,求AB的长.
22.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
23.正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=CF+AE;
(2)当AE=2时,求EF的长.
24.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形.
25.如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.
(1)若AB=2,点E是BC的中点,求线段CF的长.
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点.
②判断线段CE与EB的数量关系并说明理由.
26.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接DE,过点A作AM⊥DE,垂足为M,AM与BD相交于点F.
(1)直接写出OE与OF的数量关系:
;
(2)如图(2)若点E在AC的延长线上,AM⊥DE于点M,AM交BD的延长线于点F,其他条件不变.试探究OE与OF的数量关系,并说明理由.
27.如图,在正方形ABCD中,E,F分别是AD,CD的中点,连接BE,AF交于点M,分别延长AF,BC交于点N.
(1)求∠BMN的度数;
(2)求证:CM=AD.
参考答案
1.解:A、两组对边分别相等的四边形是平行四边形是正确的,故该选项不符合题意;
B、对角线相等的平行四边形是矩形是正确的,故该选项不符合题意;
C、对角线互相平分且垂直的四边形是菱形是正确的,故该选项不符合题意;
D、一个角是直角的四边形是矩形是错误的,故该选项符合题意;
故选:D.
2.解:∵四边形ABCD是正方形,
∴AB=AD,∠ADC=90°,∠DAC=45°,
∵AE=AB,
∴AD=AE,
∴∠ADE=∠AED=67.5°,
∴∠CDE=90°﹣67.5°=22.5°,
故选:B.
3.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠BAC=∠DAC,
∴∠BAC=∠ACB,
∴AB=BC,
∴四边形ABCD是菱形(邻边相等的平行四边形是菱形)
故选:B.
4.解:∵四边形ABCD是矩形,
∴AO=BO,∠BAD=∠ABE=90°,
∵AE平分∠BAD,
∴∠BAE=45°,
又∵∠CAE=15°,
∴∠BAO=45°+15°=60°,
∴△ABO是等边三角形,
∴AB=BO,
又∵∠BAE=45°=∠AEB,
∴AB=EB,
∴BO=BE,
∴∠BOE==75°,
∴∠COE=180°﹣∠AOB﹣∠BOE=180°﹣60°﹣75°=45°,
故选:A.
5.证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠DAE=90°,
在△ABF和△DAE中,
,
∴△ADE≌△BAF(SAS),
∴∠BAF=∠ADE,
∵∠BAD=∠DAF+∠DAO=90°,
∴∠ADE+∠DAO=90°,
∴∠AOD=90°,
∵E、F分别为AB,BC的中点,
∴AE=AB,BF=BC,
∵AB=BC,
∴AE=BF,
过C作CG⊥DE于G,
∵∠OAD+∠ADO=∠ADO+∠CDG=90°,
∴∠OAD=∠CDG,
在△ADO和△DCG中,
,
∴△ADO≌△DCG(AAS),
∴AO=DG,
∵tan∠ADE===,
∴DO=2AO=2DG,
∴DG=OG,
∴CG为DO的垂直平分线,
∴OC=DC=1,
故选:A.
6.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵EF是△ABC的中位线,
∴EF∥BC,BC=2EF,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴ED=EB=3,
∴EF=ED+DF=4,
∴BC=2EF=8,
故选:D.
7.解:①延长CB,截取BI=DF,连接AI,如图,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABE=∠ADC=90°,
∴∠ABI=90°,
在△ADF和△ABI中,
,
∴△ADF≌△ABI(SAS),
∴∠BAI=∠DAF,AI=AF,
∵∠BAD=90°,∠EAF=45°,
∴∠DAF+∠BAE=45°,
∴∠BAI+∠BAE=45°,即∠EAI=45°,
∴∠EAI=∠EAF,
∵AE=AE,
∴△AIE≌△AFE(SAS),
∴IE=FE,即DE+BF=EF,故①正确;
②过B作BD的垂线,截取BH=ND,连接AH,HM,如图,
∵四边形ABCD是正方形,
∴AD=AB,∠ADB=∠ABD=45°,∠BAD=90°,
∴∠ABH=45°=∠ADN,
在△ADN和△ABH中,
,
∴△ADN≌△ABH(SAS),
∴∠DAN=∠BAH,AN=AH,
∵∠EAF=45°,∠BAD=90°,
∴∠DAN+∠BAM=∠BAH+∠BAM=45°,
∴∠MAN=∠HAM=45°,
在△AHM和△ANM中,
,
∴△AHM≌△ANM(SAS),
∴MH=MN,
在Rt△BHM中,HM2=BH2+BM2,
∴MN2=BM2+DN2,故②正确;
③连接AC,过E作EH⊥AC于点H,
∵四边形ABCD为正方形,AB=3,
∴∠ACB=∠BAC=∠ADB=∠CAD=45°,AB=BC=3,
∴∠HEC=∠HCE=45°,
∵BE=1,
∴CE=2,
∴EH=,
∴BE≠HE,
∵∠BAE≠∠CAE,
∵∠EAF=∠CAD=45°,
∴∠CAE=∠DAF,
∴∠BAE≠∠DAF,
∴∠EAF+∠BAE≠∠ADN+∠DAF,
∵∠BAN=∠EAF+∠BAE,∠BNA=≠∠ADN+∠DAF,
∴∠BAN≠∠BNA,
∴AB≠BN,
∵AB=3,
∴BN≠3,故③错误;
④过点D作DG⊥BD过N作NG∥BC,与DG交于点G,连接CG,与AF的延长线交于点H,
∵四边形ABCD是正方形,
∴AD=CD,∠BDC=45°,∠BCD=90°
∴∠CDG=∠ADC=45°,NG⊥CD,
∴∠DNG=∠DGN=45°,
∴DN=DG,
∵∠ADN=∠CDG=45°,
∴△ADN≌△CDG(SAS),
∴∠DAN=∠DCG,
∵∠DAN+∠AFD=90°,∠AFD=∠CFH,
∴∠HCF+∠CFH=90°,
∴∠CHF=90°,
∵∠CBD=∠EAF=45°,
∴∠ABE+∠ANE=180°,
∵∠ABC=90°,
∴∠ANE=90°=∠CHF,
∴EN∥CG,
∴四边形CENG为平行四边形,
∴NG=EC=2,
∴DN=,故④正确,
故选:C.
8.解:已知AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD且点E、F不重合,
∴AE+EF=CF+EF,即AF=CE,
∴∠DEC=∠BFA=90°,
又已知AB=CD,
∴△ABF≌△CDE,
∴DE=BF,
∠DOE=∠BOF,
∴△DOE≌△BOF,
∴OE=OF,OB=OD,
∴BD和EF互相平分.
故答案为:互相平分.
9.解:∵平行四边形ABCD的对角线AC、BD交于一点O,
∴OB=OD,OA=OC,
∵点E是AD的中点,
∴AE=DE,
∴DC=2OE,
∵△BCD的周长为:DC+BC+BD=2OE+2DE+2OD=24(cm),
∴OE+DE+OD=12(cm),
则△DEO的周长是12cm.
故答案为:12.
10.证明:∵ABCD是平行四边形,
∴AB∥DC,AD=BC,
∴∠ABP=∠BPC,
∵BP平分∠ABC,
∴∠ABP=∠CBP,
∴∠BPC=∠CBP,
∵BC=BP,
∴∠BPC=∠C,
∴∠CBP=∠BPC=∠C,
∴BC=BP=PC,
∴△BPC是等边三角形,
∴∠BPC=∠PBC=∠ABP=∠BAD=60°,
∴四边形DPBA是等腰梯形,
∴∠PAB=∠ABD=43°,
∴∠APB=180°﹣60°﹣43°=77°.
故答案为:77.
11.解:连接BP,
∵四边形ABCD是正方形,
∴∠B=90°,
∵PE⊥AB,PF⊥BC,
∴四边形PEBF是矩形,
∴EF=BP,
当BP⊥AC时,BP最小,
此时,P是对角线AC、BD的交点,
∵四边形ABCD是正方形,
∴AC⊥BD,∠PBC=45°,BP=CP,
在Rt△BPC中,BP2+CP2=BC2,
即,
解得:BP=1,
∴EF=1,
故答案为:1.
12.解:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
∴∠ADB=∠BDC=45°,
∵DC=DE,
∴AD=DE,
∴∠DAE=∠DEA,
∵∠ADE=90°+52°=142°,
∴∠DAE=19°,
在△ADF和△CDF中,
,
∴△ADF≌△CDF(SAS),
∴∠DAE=∠DCF=19°,
故答案为:19.
13.解:∵E,F,M分别是正方形ABCD三边的中点,
∴AE=BE=BF=CF=DM=CM,CD∥AB,
∴四边形AMCE是平行四边形,
∴AM∥CE,故①正确;
在△DCF和△CBE中,
,
∴△DCF≌△CBE(SAS),
∴∠BCE=∠CDF,
∵∠DCE+∠BCE=90°,
∴∠CDF+∠DCN=90°,
∴∠CND=90°,
∴DF⊥CE,故②正确;
∵DF⊥CE,DM=CM,
∴DM=MN=CM,
∵AM∥CE,
∴AM⊥DN,
∴AM垂直平分DN,
∴AD=AN,
∴AN=BC,故③正确;
∵AN=BC,
∴∠ADN=∠AND,
∵DM=MN=CM,
∴∠DNM=∠NDM,∠MCN=∠MNC,
∵∠ADN+∠CDN=90°,∠CDN+∠DCN=90°,
∴∠ADN=∠DCN=∠AND=∠CNM,故④错误,
故答案为:①②③.
14.解:当点C为线段AB中点时,MN有最小值,如图,
∵AB=4,
∴AC=CB=2,
∵四边形ACDE和四边形CBGF是正方形,
∴∠ACD=∠BCF=90°,
∵M是AD中点,N是BF中点,
∴MN是△ABD的中位线,
∴MN=AB=2,
故答案为:2.
15.解:还需补充的条件可以是:∠ABC=90°,理由如下:
∵AB∥CD,且AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
故答案为:∠ABC=90°(答案不唯一).
16.解:分别延长PE、BF,交于点G,
∵四边形ABCD是矩形,AB=8,AD=6,
∴∠A=∠C=∠D=90°,BC=AD=6,AB=CD=8,
∵2∠APB+∠DPE=180°,
∴∠APB=∠GPB.
在△PAB和△PGB中,
,
∴△PAB≌△PGB(ASA),
∴PG=PA,∠A=∠G=90°,
在△DPG和△EFG中,
,
∴△DPE≌△GFE(AAS),
∴DP=DG,
∴PE+GE=DE+EF,
即PG=DF,
∴PG=DF=PA,即CF=8﹣DF=8﹣AP,
∴GF=DP=AD﹣AP,即BF=8﹣GF=8﹣(6﹣AP)=2+AP,
∵∠C=90°,
∴BC2+CF2=BF2,
即62+(8﹣AP)2=(2+AP)2,
∴AP=.
故答案为:.
17.解:过点E作EF⊥OA,垂足为F,
∵四边形OABC为菱形,∠AOC=60°,
∴∠EOA=∠AOC=30°,∠OEA=90°,
∵点A的坐标为(4,0),
∴AO=4,
则AE=OA=2,
故OE===2,
∴AO?EF=AE?OE,
则4EF=2×2,
解得:EF=,
则OF===3,
故点E的坐标为(3,).
故答案为:(3,).
18.解:连接CE、CG,如图所示:
∵四边形ACDE与四边形BCFG均是菱形,
∴∠DCE=∠ACD,∠FCG=∠BCF,
∵∠ACD+∠BCF=180°,
∴∠DCE+∠FCG=(∠ACD+∠BCF)=×180°=90°,
即∠ECG=90°,
∵H是EG的中点,CH=4,
∴EG=2CH=8
故答案为:8.
19.解:根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
①∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形;
②AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
综上所述,当P,Q同时出发4或5秒后其中一个新四边形为平行四边形.
故答案是:4或5.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
在△ADE和△CBF中,
∵,
∴△ADE≌△CBF(SAS).
(2)证明:∵E、F分别为边AB、CD的中点,
∴DF=DC,BE=AB,
又∵在?ABCD中,AB∥CD,AB=CD,
∴DF∥BE,DF=BE,
∴四边形DEBF为平行四边形,
∵DB⊥BC,
∴∠DBC=90°,
∴△DBC为直角三角形,
又∵F为边DC的中点,
∴BF=DC=DF,
又∵四边形DEBF为平行四边形,
∴四边形DEBF是菱形.
21.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CAE=∠ACF,∠CFO=∠AEO,
在△AOE和△COF中,,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:连接OB,如图所示:
∵BF=BE,OE=OF,
∴BO⊥EF,
由(1)知,△AOE≌△COF,
∴OA=OC,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴BO=AC=OA,
∴∠BAC=∠OBA,
又∠BEF=2∠BAC,
∴∠BEF=2∠OBE,
而Rt△OBE中,∠BEO+∠OBE=90°,
∴∠BAC=30°,
∴BC=AC=3,
∴AB==9.
22.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DM=EC=4.
23.(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,AE=CM,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF,
∴EF=CF+AE;
(2)解:设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
则EF=5.
24.(1)证明:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
在△ABF和△ADF中,
,
∴△ABF≌△ADF,
∴∠AFD=∠AFB,
∵∠AFB=∠AFD,
∴∠AFD=∠CFE;
(2)证明:∵AB∥CD,
∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形.
25.解:(1)∵在正方形ABCD中,AD∥BC,
∴∠DAG=∠F,
又∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF,
∵AB=2,∠B=90°,点E为BC的中点,
∴BE=EC=1,
∴AE==,
∴EF=,
∴CF=EF﹣EC=﹣1;
(2)①证明:∵EA=EF,EG⊥AF,
∴AG=FG,
在△ADG和△FCG中
,
∴△ADG≌△FCG(AAS),
∴DG=CG,
即点G为CD的中点;
②设CD=2a,则CG=a,
由①知,CF=DA=2a,
∵EG⊥AF,∠GCF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,
∴∠EGC=∠F,
∴CE=EB.
26.解:(1)∵正方形ABCD的对角线AC、BD相交于点O,AM⊥DE,
∴∠AOD=∠DOE=∠AME=90°,OA=OD,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠AFO=∠MEA,
在△AOF和△DOE中,
,
∴△AOF≌△BOE(ASA),
∴OE=OF,
故答案为:OE=OF;
(2)OE=OF,
理由如下:
∵正方形ABCD的对角线AC、BD相交于点O,AM⊥DE,
∴∠AOD=∠DOE=∠AME=90°,OA=OD,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠AFO=∠MEA,
在△AOF和△DOE中,
,
∴△AOF≌△BOE(ASA),
∴OE=OF.
27.解:(1)∵四边形ABCD是正方形,
∴AD=CD=AB,∠BAD=∠D=90°,
∵E、F分别是AD、CD的中点,
∴AE=AD,DF=CD,
∴AE=DF,
在△ABE和△DAF中,
,
∴△ABE≌△DAF(SAS),
∴AF=BE,∠AEB=∠AFD,
在直角△ADF中,∠DAF+∠AFD=90°,
∴∠DAF+∠AEB=90°,
∴∠AME=90°,
∴AF⊥BE,
∴∠BMN=90°;
(2)证明:∵DF=CF,∠D=∠FCN=90°,∠AFD=∠NFC,
在△ADF和△NCF中,
,
∴△ADF≌△NCF(ASA),
∴AD=CN=CD=BC,
在直角△BMN中,BC=CN,
∴CM=BN=BC=AD.
1.下列说法不正确的是( )
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.一个角是直角的四边形是矩形
2.如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则∠CDE的度数为( )
A.20°
B.22.5°
C.25°
D.30°
3.已知平行四边形ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为菱形的是( )
A.∠BAC=∠DCA
B.∠BAC=∠DAC
C.∠BAC=∠ABD
D.∠BAC=∠ADB
4.如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=15°,则∠COE=( )
A.45°
B.60°
C.75°
D.30°
5.如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE,AF,DE与AF交于点O.连接OC,则OC=( )
A.1
B.
C.
D.
6.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2
B.4
C.6
D.8
7.如图,正方形ABCD中,∠EAF=45°,有以下四个结论:
①BE+DF=EF;
②BM2+DN2=MN2
③若AB=3,BE=1,则BN=3;
④若CE=2,则DN=,其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
8.如图,点A、E、F、C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD.则当点E、F不重合时,BD与EF的关系是
.
9.如图平行四边形ABCD的对角线AC、BD交于一点O,点E是AD的中点,△BCD的周长为24cm,则△DEO的周长是
cm.
10.如图,在?ABCD中,P为CD上一点,BC=BP,BP平分∠ABC,∠ABD=43°,则∠APB的度数是
度.
11.正方形ABCD的边长为,点P为对角线AC上一个动点,PE⊥AB,PF⊥CB,垂足分别是E,F.当P在AC上移动时,线段EF的最小值是
.
12.如图,点E为正方形ABCD外一点,ED=CD,AE与BD相交于点F.若∠CDE=52°,则∠DCF=
°.
13.如图,E,F,M分别是正方形ABCD三边的中点,CE与DF交于N,连接AM,AN,MN对于下列四个结论:①AM∥CE;②DF⊥CE;③AN=BC;④∠AND=∠CMN.其中正确的是
.(填序号)
14.点C是线段AB上的动点,分别以AC,BC为边向上方作正方形ACDE,正方形CBGF,连接AD,AD,BF的中点M,N,若AB=4,则MN的最小值为
.
15.如图,在四边形ABCD中,AB∥CD,AB=CD,要使四边形ABCD为矩形,还需补充的条件可以是:
(写1个即可).
16.如图,在矩形ABCD中,AB=8,AD=6,点E,F都在CD上,点P在AD上,连接PE,若EF=PE,∠FBP=∠ABP,2∠APB+∠DPE=180°,则线段AP的长为
.
17.如图,平面直角坐标系中,四边形OABC为菱形,点A在x轴正半轴上,点A的坐标为(4,0),∠AOC=60°,对角线OB,AC相交于点E,则点E的坐标为
.
18.如图,在线段AB上取一点C,分别以AC,BC为边长作菱形BCFG和菱形ACDE,使点D在边CF上,连接EG,H是EG的中点,且CH=4,则EG的长是
.
19.如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发
秒后其中一个新四边形为平行四边形.
20.如图,在?ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
21.如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若AC=6,求AB的长.
22.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
23.正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=CF+AE;
(2)当AE=2时,求EF的长.
24.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形.
25.如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.
(1)若AB=2,点E是BC的中点,求线段CF的长.
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点.
②判断线段CE与EB的数量关系并说明理由.
26.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接DE,过点A作AM⊥DE,垂足为M,AM与BD相交于点F.
(1)直接写出OE与OF的数量关系:
;
(2)如图(2)若点E在AC的延长线上,AM⊥DE于点M,AM交BD的延长线于点F,其他条件不变.试探究OE与OF的数量关系,并说明理由.
27.如图,在正方形ABCD中,E,F分别是AD,CD的中点,连接BE,AF交于点M,分别延长AF,BC交于点N.
(1)求∠BMN的度数;
(2)求证:CM=AD.
参考答案
1.解:A、两组对边分别相等的四边形是平行四边形是正确的,故该选项不符合题意;
B、对角线相等的平行四边形是矩形是正确的,故该选项不符合题意;
C、对角线互相平分且垂直的四边形是菱形是正确的,故该选项不符合题意;
D、一个角是直角的四边形是矩形是错误的,故该选项符合题意;
故选:D.
2.解:∵四边形ABCD是正方形,
∴AB=AD,∠ADC=90°,∠DAC=45°,
∵AE=AB,
∴AD=AE,
∴∠ADE=∠AED=67.5°,
∴∠CDE=90°﹣67.5°=22.5°,
故选:B.
3.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠BAC=∠DAC,
∴∠BAC=∠ACB,
∴AB=BC,
∴四边形ABCD是菱形(邻边相等的平行四边形是菱形)
故选:B.
4.解:∵四边形ABCD是矩形,
∴AO=BO,∠BAD=∠ABE=90°,
∵AE平分∠BAD,
∴∠BAE=45°,
又∵∠CAE=15°,
∴∠BAO=45°+15°=60°,
∴△ABO是等边三角形,
∴AB=BO,
又∵∠BAE=45°=∠AEB,
∴AB=EB,
∴BO=BE,
∴∠BOE==75°,
∴∠COE=180°﹣∠AOB﹣∠BOE=180°﹣60°﹣75°=45°,
故选:A.
5.证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠DAE=90°,
在△ABF和△DAE中,
,
∴△ADE≌△BAF(SAS),
∴∠BAF=∠ADE,
∵∠BAD=∠DAF+∠DAO=90°,
∴∠ADE+∠DAO=90°,
∴∠AOD=90°,
∵E、F分别为AB,BC的中点,
∴AE=AB,BF=BC,
∵AB=BC,
∴AE=BF,
过C作CG⊥DE于G,
∵∠OAD+∠ADO=∠ADO+∠CDG=90°,
∴∠OAD=∠CDG,
在△ADO和△DCG中,
,
∴△ADO≌△DCG(AAS),
∴AO=DG,
∵tan∠ADE===,
∴DO=2AO=2DG,
∴DG=OG,
∴CG为DO的垂直平分线,
∴OC=DC=1,
故选:A.
6.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵EF是△ABC的中位线,
∴EF∥BC,BC=2EF,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴ED=EB=3,
∴EF=ED+DF=4,
∴BC=2EF=8,
故选:D.
7.解:①延长CB,截取BI=DF,连接AI,如图,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABE=∠ADC=90°,
∴∠ABI=90°,
在△ADF和△ABI中,
,
∴△ADF≌△ABI(SAS),
∴∠BAI=∠DAF,AI=AF,
∵∠BAD=90°,∠EAF=45°,
∴∠DAF+∠BAE=45°,
∴∠BAI+∠BAE=45°,即∠EAI=45°,
∴∠EAI=∠EAF,
∵AE=AE,
∴△AIE≌△AFE(SAS),
∴IE=FE,即DE+BF=EF,故①正确;
②过B作BD的垂线,截取BH=ND,连接AH,HM,如图,
∵四边形ABCD是正方形,
∴AD=AB,∠ADB=∠ABD=45°,∠BAD=90°,
∴∠ABH=45°=∠ADN,
在△ADN和△ABH中,
,
∴△ADN≌△ABH(SAS),
∴∠DAN=∠BAH,AN=AH,
∵∠EAF=45°,∠BAD=90°,
∴∠DAN+∠BAM=∠BAH+∠BAM=45°,
∴∠MAN=∠HAM=45°,
在△AHM和△ANM中,
,
∴△AHM≌△ANM(SAS),
∴MH=MN,
在Rt△BHM中,HM2=BH2+BM2,
∴MN2=BM2+DN2,故②正确;
③连接AC,过E作EH⊥AC于点H,
∵四边形ABCD为正方形,AB=3,
∴∠ACB=∠BAC=∠ADB=∠CAD=45°,AB=BC=3,
∴∠HEC=∠HCE=45°,
∵BE=1,
∴CE=2,
∴EH=,
∴BE≠HE,
∵∠BAE≠∠CAE,
∵∠EAF=∠CAD=45°,
∴∠CAE=∠DAF,
∴∠BAE≠∠DAF,
∴∠EAF+∠BAE≠∠ADN+∠DAF,
∵∠BAN=∠EAF+∠BAE,∠BNA=≠∠ADN+∠DAF,
∴∠BAN≠∠BNA,
∴AB≠BN,
∵AB=3,
∴BN≠3,故③错误;
④过点D作DG⊥BD过N作NG∥BC,与DG交于点G,连接CG,与AF的延长线交于点H,
∵四边形ABCD是正方形,
∴AD=CD,∠BDC=45°,∠BCD=90°
∴∠CDG=∠ADC=45°,NG⊥CD,
∴∠DNG=∠DGN=45°,
∴DN=DG,
∵∠ADN=∠CDG=45°,
∴△ADN≌△CDG(SAS),
∴∠DAN=∠DCG,
∵∠DAN+∠AFD=90°,∠AFD=∠CFH,
∴∠HCF+∠CFH=90°,
∴∠CHF=90°,
∵∠CBD=∠EAF=45°,
∴∠ABE+∠ANE=180°,
∵∠ABC=90°,
∴∠ANE=90°=∠CHF,
∴EN∥CG,
∴四边形CENG为平行四边形,
∴NG=EC=2,
∴DN=,故④正确,
故选:C.
8.解:已知AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD且点E、F不重合,
∴AE+EF=CF+EF,即AF=CE,
∴∠DEC=∠BFA=90°,
又已知AB=CD,
∴△ABF≌△CDE,
∴DE=BF,
∠DOE=∠BOF,
∴△DOE≌△BOF,
∴OE=OF,OB=OD,
∴BD和EF互相平分.
故答案为:互相平分.
9.解:∵平行四边形ABCD的对角线AC、BD交于一点O,
∴OB=OD,OA=OC,
∵点E是AD的中点,
∴AE=DE,
∴DC=2OE,
∵△BCD的周长为:DC+BC+BD=2OE+2DE+2OD=24(cm),
∴OE+DE+OD=12(cm),
则△DEO的周长是12cm.
故答案为:12.
10.证明:∵ABCD是平行四边形,
∴AB∥DC,AD=BC,
∴∠ABP=∠BPC,
∵BP平分∠ABC,
∴∠ABP=∠CBP,
∴∠BPC=∠CBP,
∵BC=BP,
∴∠BPC=∠C,
∴∠CBP=∠BPC=∠C,
∴BC=BP=PC,
∴△BPC是等边三角形,
∴∠BPC=∠PBC=∠ABP=∠BAD=60°,
∴四边形DPBA是等腰梯形,
∴∠PAB=∠ABD=43°,
∴∠APB=180°﹣60°﹣43°=77°.
故答案为:77.
11.解:连接BP,
∵四边形ABCD是正方形,
∴∠B=90°,
∵PE⊥AB,PF⊥BC,
∴四边形PEBF是矩形,
∴EF=BP,
当BP⊥AC时,BP最小,
此时,P是对角线AC、BD的交点,
∵四边形ABCD是正方形,
∴AC⊥BD,∠PBC=45°,BP=CP,
在Rt△BPC中,BP2+CP2=BC2,
即,
解得:BP=1,
∴EF=1,
故答案为:1.
12.解:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
∴∠ADB=∠BDC=45°,
∵DC=DE,
∴AD=DE,
∴∠DAE=∠DEA,
∵∠ADE=90°+52°=142°,
∴∠DAE=19°,
在△ADF和△CDF中,
,
∴△ADF≌△CDF(SAS),
∴∠DAE=∠DCF=19°,
故答案为:19.
13.解:∵E,F,M分别是正方形ABCD三边的中点,
∴AE=BE=BF=CF=DM=CM,CD∥AB,
∴四边形AMCE是平行四边形,
∴AM∥CE,故①正确;
在△DCF和△CBE中,
,
∴△DCF≌△CBE(SAS),
∴∠BCE=∠CDF,
∵∠DCE+∠BCE=90°,
∴∠CDF+∠DCN=90°,
∴∠CND=90°,
∴DF⊥CE,故②正确;
∵DF⊥CE,DM=CM,
∴DM=MN=CM,
∵AM∥CE,
∴AM⊥DN,
∴AM垂直平分DN,
∴AD=AN,
∴AN=BC,故③正确;
∵AN=BC,
∴∠ADN=∠AND,
∵DM=MN=CM,
∴∠DNM=∠NDM,∠MCN=∠MNC,
∵∠ADN+∠CDN=90°,∠CDN+∠DCN=90°,
∴∠ADN=∠DCN=∠AND=∠CNM,故④错误,
故答案为:①②③.
14.解:当点C为线段AB中点时,MN有最小值,如图,
∵AB=4,
∴AC=CB=2,
∵四边形ACDE和四边形CBGF是正方形,
∴∠ACD=∠BCF=90°,
∵M是AD中点,N是BF中点,
∴MN是△ABD的中位线,
∴MN=AB=2,
故答案为:2.
15.解:还需补充的条件可以是:∠ABC=90°,理由如下:
∵AB∥CD,且AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
故答案为:∠ABC=90°(答案不唯一).
16.解:分别延长PE、BF,交于点G,
∵四边形ABCD是矩形,AB=8,AD=6,
∴∠A=∠C=∠D=90°,BC=AD=6,AB=CD=8,
∵2∠APB+∠DPE=180°,
∴∠APB=∠GPB.
在△PAB和△PGB中,
,
∴△PAB≌△PGB(ASA),
∴PG=PA,∠A=∠G=90°,
在△DPG和△EFG中,
,
∴△DPE≌△GFE(AAS),
∴DP=DG,
∴PE+GE=DE+EF,
即PG=DF,
∴PG=DF=PA,即CF=8﹣DF=8﹣AP,
∴GF=DP=AD﹣AP,即BF=8﹣GF=8﹣(6﹣AP)=2+AP,
∵∠C=90°,
∴BC2+CF2=BF2,
即62+(8﹣AP)2=(2+AP)2,
∴AP=.
故答案为:.
17.解:过点E作EF⊥OA,垂足为F,
∵四边形OABC为菱形,∠AOC=60°,
∴∠EOA=∠AOC=30°,∠OEA=90°,
∵点A的坐标为(4,0),
∴AO=4,
则AE=OA=2,
故OE===2,
∴AO?EF=AE?OE,
则4EF=2×2,
解得:EF=,
则OF===3,
故点E的坐标为(3,).
故答案为:(3,).
18.解:连接CE、CG,如图所示:
∵四边形ACDE与四边形BCFG均是菱形,
∴∠DCE=∠ACD,∠FCG=∠BCF,
∵∠ACD+∠BCF=180°,
∴∠DCE+∠FCG=(∠ACD+∠BCF)=×180°=90°,
即∠ECG=90°,
∵H是EG的中点,CH=4,
∴EG=2CH=8
故答案为:8.
19.解:根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
①∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形;
②AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
综上所述,当P,Q同时出发4或5秒后其中一个新四边形为平行四边形.
故答案是:4或5.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
在△ADE和△CBF中,
∵,
∴△ADE≌△CBF(SAS).
(2)证明:∵E、F分别为边AB、CD的中点,
∴DF=DC,BE=AB,
又∵在?ABCD中,AB∥CD,AB=CD,
∴DF∥BE,DF=BE,
∴四边形DEBF为平行四边形,
∵DB⊥BC,
∴∠DBC=90°,
∴△DBC为直角三角形,
又∵F为边DC的中点,
∴BF=DC=DF,
又∵四边形DEBF为平行四边形,
∴四边形DEBF是菱形.
21.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CAE=∠ACF,∠CFO=∠AEO,
在△AOE和△COF中,,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:连接OB,如图所示:
∵BF=BE,OE=OF,
∴BO⊥EF,
由(1)知,△AOE≌△COF,
∴OA=OC,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴BO=AC=OA,
∴∠BAC=∠OBA,
又∠BEF=2∠BAC,
∴∠BEF=2∠OBE,
而Rt△OBE中,∠BEO+∠OBE=90°,
∴∠BAC=30°,
∴BC=AC=3,
∴AB==9.
22.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DM=EC=4.
23.(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,AE=CM,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF,
∴EF=CF+AE;
(2)解:设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
则EF=5.
24.(1)证明:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
在△ABF和△ADF中,
,
∴△ABF≌△ADF,
∴∠AFD=∠AFB,
∵∠AFB=∠AFD,
∴∠AFD=∠CFE;
(2)证明:∵AB∥CD,
∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形.
25.解:(1)∵在正方形ABCD中,AD∥BC,
∴∠DAG=∠F,
又∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF,
∵AB=2,∠B=90°,点E为BC的中点,
∴BE=EC=1,
∴AE==,
∴EF=,
∴CF=EF﹣EC=﹣1;
(2)①证明:∵EA=EF,EG⊥AF,
∴AG=FG,
在△ADG和△FCG中
,
∴△ADG≌△FCG(AAS),
∴DG=CG,
即点G为CD的中点;
②设CD=2a,则CG=a,
由①知,CF=DA=2a,
∵EG⊥AF,∠GCF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,
∴∠EGC=∠F,
∴CE=EB.
26.解:(1)∵正方形ABCD的对角线AC、BD相交于点O,AM⊥DE,
∴∠AOD=∠DOE=∠AME=90°,OA=OD,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠AFO=∠MEA,
在△AOF和△DOE中,
,
∴△AOF≌△BOE(ASA),
∴OE=OF,
故答案为:OE=OF;
(2)OE=OF,
理由如下:
∵正方形ABCD的对角线AC、BD相交于点O,AM⊥DE,
∴∠AOD=∠DOE=∠AME=90°,OA=OD,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠AFO=∠MEA,
在△AOF和△DOE中,
,
∴△AOF≌△BOE(ASA),
∴OE=OF.
27.解:(1)∵四边形ABCD是正方形,
∴AD=CD=AB,∠BAD=∠D=90°,
∵E、F分别是AD、CD的中点,
∴AE=AD,DF=CD,
∴AE=DF,
在△ABE和△DAF中,
,
∴△ABE≌△DAF(SAS),
∴AF=BE,∠AEB=∠AFD,
在直角△ADF中,∠DAF+∠AFD=90°,
∴∠DAF+∠AEB=90°,
∴∠AME=90°,
∴AF⊥BE,
∴∠BMN=90°;
(2)证明:∵DF=CF,∠D=∠FCN=90°,∠AFD=∠NFC,
在△ADF和△NCF中,
,
∴△ADF≌△NCF(ASA),
∴AD=CN=CD=BC,
在直角△BMN中,BC=CN,
∴CM=BN=BC=AD.
